Prasanna

RD Sharma Class 9 Solutions Chapter 19 Surface Areas and Volume of a Circular Cylinder Ex 19.1

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 19 Surface Areas and Volume of a Circular Cylinder Ex 19.1

Other Exercises

• RD Sharma Class 9 Solutions Chapter 19 Surface Areas and Volume of a Circular Cylinder Ex 19.1
• RD Sharma Class 9 Solutions Chapter 19 Surface Areas and Volume of a Circular Cylinder Ex 19.2
• RD Sharma Class 9 Solutions Chapter 19 Surface Areas and Volume of a Circular Cylinder VSAQS
• RD Sharma Class 9 Solutions Chapter 19 Surface Areas and Volume of a Circular Cylinder MCQS

Question 1.
Curved surface area of a right circular cylinder is 4.4 m2. If the radius of the base of the cylinder is 0.7 m, find its height. [NCERT]
Solution:
Curved surface area of a cylinder = 4.4 m²
Radius (r) = 0.7 m

Question 2.
In a hot water heating system, there is a cylindrical pipe of length 28 m and diameter 5 cm. Find the total radiating surface in the system. [NCERT]
Solution:
Diameter of the pipe = 5 cm

Question 3.
A cylindrical pillar is 50 cm in diameter and 3.5 m in height. Find the cost of painting the curved surface of the pillar at the rate of 12.50 per m². [NCERT]
Solution:
Diameter of cylindrical pillar = 50 cm

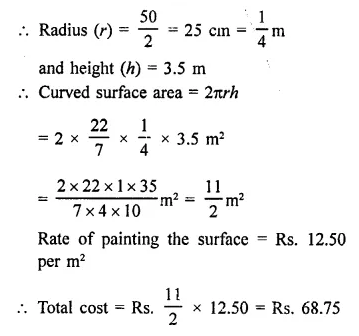
Question 4.
It is required to make a closed cylindrical tank of height 1 m and base diameter 140 cm from a metal sheet. How many square metres of the sheet are required for the same? [NCERT]
Solution:
Height of cylinder (h) = 1 m = 100 cm
Diameter of box = 140 cm

Question 5.
The total surface area of a hollow cylinder which is open from both sides is 4620 sq. cm, area of base ring is 115.5 sq. cm and height 7 cm. Find the thickness of the cylinder.
Solution:
Total surface area of a hollow cylinder open from both sides = 4620 cm²
Area of base of ring = 115.5 cm²
Height (h) = 7 cm
Let outer radius (R) = R
and inner radius = r

Question 6.
Find the ratio between the total surface area of a cylinder to its curved surface area, given that its height and radius are 7.5 cm and 3.5 cm.
Solution:
Radius of the cylinder (r) = 3.5 cm
and height (h) = 7.5 cm
Total surface area = 2πr (h + r)
and curved surface area = 2πrh

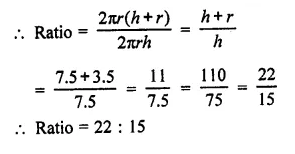
Question 7.
A cylindrical vessel, without lid, has to be tin-coated on its both sides. If the radius of the base is 70 cm and its height is 1.4 m, calculate the cost of tin-coating at the rate of ₹3.50 per 1000 cm².
Solution:
Radius of the base of a cylindrical vessel (r) = 70 cm
and height (h) = 1.4 m = 140 cm
Total surface area (excluding upper lid) on both sides = 2πrh x 2 + πr² x 2

Question 8.
The inner diameter of a circular well is 3.5 m. It is 10 m deep. Find:
(i) inner curved surface area.
(ii) the cost of plastering this curved surface at the rate of ₹40 per m². [NCERT]
Solution:
Inner diameter of a well = 3.5 m

Question 9.
The students of a Vidyalaya were asked to participate s a competition for making and decorating pen holders in the shape of a cylinder with a base, using cardboard. Each pen holder was to be of radius 3 cm and height 10.5 cm. The Vidyalaya was to supply the competitors with cardboard. If there were 35 competitors, how much cardboard was required to be bought for the competition? [NCERT]
Solution:
Radius of cylinderical pen holder (r) = 3 cm
Height (h) = 10.5 cm
∴ Surface area of the pen holder

Question 10.
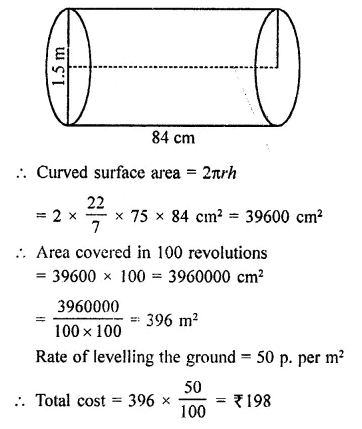
The diameter of roller 1.5 m long is 84 cm. If it takes 100 revolutions to level a play¬ground, find the cost of levelling this ground at the rate of 50 paise per square metre.
Solution:
Diameter of a roller = 1.5 m
∴ Radius = \(\frac { 1.5 }{ 2 }\) = 0.75 m = 75 cm
and length (h) = 84 cm

Question 11.
Twenty cylindrical pillars of the Parliament House are to be cleaned. If the diameter of each pillar is 0.50 m and height is 4 m. What will be the cost of cleaning them at the rate of ₹2.50 per square metre? [NCERT]
Solution:
Number of pillars = 20
Diameter of one pillar = 0.50 m

Question 12.
A solid cylinder has total surface area of 462 cm². Its curved surface area is one- third of its total surface area. Find the radius and height of the cylinder.
Solution:
Total surface of solid cylinder = 462 cm²
Curved surface area = \(\frac { 1 }{ 3 }\) of total surface area

Question 13.
The total surface area of a hollow metal cylinder, open at both ends of external radius 8 cm and height 10 cm is 338 π cm². Taking r to be inner radius, obtain an equation in r and use it to obtain the thickness of the metal in the cylinder.
Solution:
Total surface area of a hollow metal cylinder = 338π cm²
Let R be the outer radius, r be inner radius and h be the height of the cylinder of the cylinder
∴ 2πRh + 2πrh + 2πR² – 2πr² = 338π
R = 8 cm, h = 10 cm
⇒ 2πh (R + r) + 2π(R² – r²) = 338π
⇒ Dividing by 2π , we get
⇒ h(R + r) + (R² – r²) = 169
⇒ 10(8 + r) + (8 + r) (8 – r) = 169
⇒ 80 + 10r + 64 – r² = 169
⇒ 10r – r² + 144 – 169 = 0
⇒ r² – 10r + 25 = 0
⇒ (r-5)² = 0
⇒ r = 5
∴ Thickness of the metal = R – r = 8 – 5 = 3 cm

Question 14.
Find the lateral curved surface area of a cylinderical petrol storage tank that is 4.2m in diameter and 4.5 m high. How much steel was actually used, if \(\frac { 1 }{ 12 }\) of steel actually used was wasted in making the closed tank? [NCERT]
Solution:
Diameter of a cylinderical tank = 4.2 m

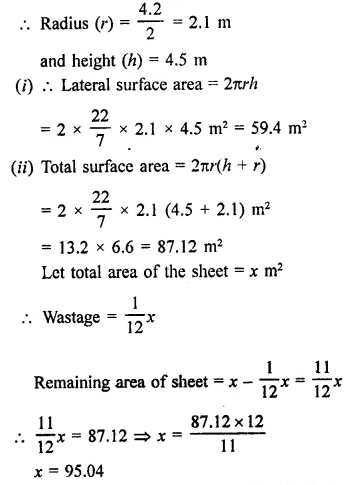
Hope given RD Sharma Class 9 Solutions Chapter 19 Surface Areas and Volume of a Circular Cylinder Ex 19.1 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 9 Solutions Chapter 18 Surface Areas and Volume of a Cuboid and Cube MCQS

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 18 Surface Areas and Volume of a Cuboid and Cube MCQS

Other Exercises

• RD Sharma Class 9 Solutions Chapter 18 Surface Areas and Volume of a Cuboid and Cube Ex 18.1
• RD Sharma Class 9 Solutions Chapter 18 Surface Areas and Volume of a Cuboid and Cube Ex 18.2
• RD Sharma Class 9 Solutions Chapter 18 Surface Areas and Volume of a Cuboid and Cube VSAQS
• RD Sharma Class 9 Solutions Chapter 18 Surface Areas and Volume of a Cuboid and Cube MCQS

Mark correct alternative in each of the following:
Question 1.
The length of the longest rod that can be fitted in a cubical vessel of edge 10 cm long, is
(a) 10 cm
(b) 10\(\sqrt { 2 } \) cm
(c) 10\(\sqrt { 3 } \) cm
(d) 20 cm
Solution:
Edge of cuboid (a) = 10 cm
∴ Longest edge = \(\sqrt { 3 } \) a cm
= \(\sqrt { 3 } \) x 10 = 10\(\sqrt { 3 } \) cm (c)

Question 2.
Three equal cubes are placed adjacently in a row. The ratio of the total surface area of the resulting cuboid to that of the sum of the surface areas of three cubes, is
(a) 7 : 9
(b) 49 : 81
(c) 9 : 7
(d) 27 : 23
Solution:
Let a be the side of three equal cubes
∴ Surface area of 3 cubes
= 3 x 6a² = 18a²
and length of so formed cuboid = 3a
Breadth = a
and height = a
∴ Surface area = 2(lb + bh + hl)
= 2[3a x a + a x a+a x 3a] = 2[3a² + a² + 3a²] = 2 x 7a² = 14a²
∴ Ratio in the surface areas of cuboid and three cubes = 14a² : 18a²= 7:9 (a)

Question 3.
If the length of a diagonal of a cube is 8 \(\sqrt { 3 } \) cm, then its surface area is
(a) 512 cm²
(b) 384 cm²
(c) 192 cm²
(d) 768 cm²
Solution:
Length of the diagonal of cube = 8 \(\sqrt { 3 } \) cm

Question 4.
If the volumes of two cubes are in the ratio 8:1, then the ratio of their edges is
(a) 8 : 1
(b) 2\(\sqrt { 2 } \) : 1
(c) 2 : 1
(d) none of these
Solution:
Let volume of first cube = 8x³
and of second cube = x³

Question 5.
The volume of a cube whose surface area is 96 cm², is
(a) 16\(\sqrt { 2 } \) cm³
(b) 32 cm³
(c) 64 cm³
(d) 216 cm³
Solution:
Surface area of a cube = 96 cm²

Question 6.
The length, width and height of a rectangular solid are in the ratio of 3 : 2 : 1. If the volume of the box is 48 cm³, the total surface area of the box is
(a) 27 cm²
(b) 32 cm²
(c) 44 cm²
(d) 88 cm²
Solution:
Ratio in the dimensions of a cuboid =3 : 2 : 1
Let length = 3x
Breadth = 2x
and height = x
Then volume = lbh = 3x x 2x x x = 6×3
∴ 6x³ = 48 ⇒ x³= \(\frac { 48 }{ 6 }\) = 8 = (2)³
∴ x = 2
∴ Length (l) = 3 x 2 = 6 cm
Breadth (b) = 2 x 2 = 4 cm
Height (h) = 1 x 2 = 2 cm
Now surface area = 2[lb + bh + hl]
= 2[6 x 4 + 4 x 2 + 2 x 6] cm²
= 2[24 + 8-+ 12] = 2 x 44 cm²
= 88 cm² (d)

Question 7.
If the areas of the adjacent faces of a rectangular block are in the ratio 2:3:4 and its volume is 9000 cm3, then the length of the shortest edge is
(a) 30 cm
(b) 20 cm
(c) 15 cm
(d) 10 cm
Solution:
Ratio in the areas of three adjacent faces of a cuboid = 2 : 3 : 4
Volume = 9000 cm³
Let the area of faces be 2x, 3x, Ax and
Let a, b, and c be the dimensions of the cuboid, then
∴ 2x = ab, 3x = be, 4x = ca
∴ ab x be x ca = 2x x 3x x 4x
a²b²c² = 24 x 3
But volume = abc = 9000 cm³

Question 8.
If each edge of a cube, of volume V, is doubled, then the volume of the new cube is
(a) 2V
(b) 4V
(c) 6V
(d) 8V
Solution:
Let a be the edge of a cube whose Volume = V
∴ a3 = V
By doubling the edge, we get 2a
Then volume = (2a)3 = 8a³
∴ Volume of new cube = 8a³ = 8V (d)

Question 9.
If each edge of a cuboid of surface area S is doubled, then surface area of the new cuboid is
(a) 2S
(b) 4S
(c) 6S
(d) 8S
Solution:
Let each edge of a cube = a
Then surface area = 6a²
∴ S = 6a²
Now doubling the edge, we get
New edge of a new cube = 2a
∴ Surface area = 6(2a)²
= 6 x 4a² = 24a²
= 4 x 6a² = 4S (b)

Question 10.
The area of the floor of a room is 15 m2. If its height is 4 m, then the volume of the air contained in the room is
(a) 60 dm³
(b) 600 dm³
(c) 6000 dm³
(d) 60000 dm³
Solution:
Area of a floor of a room = 15 m²
Height (h) = 4 m
∴ Volume of air in the room = Floor area x Height
= 15 m² x 4 m = 60 m³
= 60 x 10 x 10 x 10 dm² = 60000 dm² (d)

Question 11.
The cost of constructing a wall 8 m long, 4 m high and 20 cm thick at the rate of ₹25 per m³ is
(a) ₹16
(b) ₹80
(c) ₹160
(d) ₹320
Solution:
Length of wall (l) = 8 m
Breadth (b) = 20 cm = \(\frac { 1 }{ 5 }\) m
Height (h) = 4 m

Question 12.
10 cubic metres clay in uniformaly spread on a land of area 10 acres. The rise in the level of the ground is
(a) 1 cm
(b) 10 cm
(c) 100 cm
(d) 1000 cm
Solution:
Volume of clay = 10 m³
Area of land = 10 acres
= 10 x 100 = 1000 m²
∴ Rise of level by spreading the clay

Question 13.
Volume of a cuboid is 12 cm³. The volume (in cm³) of a cuboid whose sides are double of the above cuboid is
(a) 24
(b) 48
(c) 72
(d) 96
Solution:
Volume of cuboid = 12 cm³
By doubling the sides of the cuboid the
volume will be = 12 cm³ x 2 x 2 x 2
= 96 cm³ (d)

Question 14.
If the sum of all the edges of a cube is 36 cm, then the volume (in cm3) of that cube is
(a) 9
(b) 27
(c) 219
(d) 729
Solution:
Sum of all edges of a cube = 36 cm
No. of edge of a cube are 12
∴ Length of its one edge = \(\frac { 36 }{ 12 }\) = 3 cm
Then volume = (edge)³ = (3)³ cm³
= 27 cm³ (b)

Question 15.
The number of cubes of side 3 cm that can be cut from a cuboid of dimensions 9 cm x 9 cm x 6 cm, is
(a) 9
(b) 10
(c) 18
(d) 20
Solution:
Dimensions of a cuboid = 9 cm x 9 cm x 6 cm

Question 16.
On a particular day, the rain fall recorded in a terrace 6 m long and 5 m broad is 15 cm. The quantity of water collected in the terrace is
(a) 300 litres
(b) 450 litres
(c) 3000 litres
(d) 4500 litres
Solution:
Dimension of a terrace = 6mx5m
Level of rain on it = 15 cm
∴ Volume of water collected on it

Question 17.
If A₁, A₂ and A₃ denote the areas of three adjacent faces of a cuboid, then its volume is

Solution:
Let l, b, h be the dimensions of the cuboid
∴ A₁= lb, A₂ = bh, A₃ = hl
∴ A₁ A₂ A₃ = lb.bh.hl = l₂b₂h₂

Question 18.
If l is the length of a diagonal of a cube of volume V, then

Solution:
Volume of a cube = V
and longest diagonal = l

Question 19.
If V is the volume of a cuboid of dimensions x, y, z and A is its surface area, then \(\frac { A }{ V }\)

Solution:
A is surface area, V is volume and x, y and z are the dimensions
Then V = xyz
A = 2[xy + yz + zx]

Question 20.
The sum of the length, breadth and depth of a cuboid is 19 cm and its diagonal is 5\(\sqrt { 5 } \) cm. Its surface area is
(a) 361 cm²
(b) 125 cm²
(c) 236 cm²
(d) 486 cm²
Solution:
Let x, y, z be the dimensions of a cuboid,
then x + y + z = 19 cm

Question 21.
If each edge of a cube is increased by 50%, the percentage increase in its surface area is
(a) 50%
(b) 75%
(c) 100%
(d) 125%
Solution:
Let in first case, edge of a cube = a
Then surface area = 6a²
In second case, increase in side = 50%

Question 22.
A cube whose volume is 1/8 cubic centimeter is placed on top of a cube whose volume is. 1 cm³. The two ,cubes are then placed on top of a third cube whose volume is 8 cm³. The height of the stacked cubes is
(a) 3.5 cm
(b) 3 cm
(c) 7 cm
(d) none of these
Solution:
Volume of first cube = \(\frac { 1 }{ 2 }\) cm³

Hope given RD Sharma Class 9 Solutions Chapter 18 Surface Areas and Volume of a Cuboid and Cube MCQS are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.