RD Sharma Class 9 Solutions Chapter 18 Surface Areas and Volume of a Cuboid and Cube MCQS
These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 18 Surface Areas and Volume of a Cuboid and Cube MCQS
Other Exercises
- RD Sharma Class 9 Solutions Chapter 18 Surface Areas and Volume of a Cuboid and Cube Ex 18.1
- RD Sharma Class 9 Solutions Chapter 18 Surface Areas and Volume of a Cuboid and Cube Ex 18.2
- RD Sharma Class 9 Solutions Chapter 18 Surface Areas and Volume of a Cuboid and Cube VSAQS
- RD Sharma Class 9 Solutions Chapter 18 Surface Areas and Volume of a Cuboid and Cube MCQS
Mark correct alternative in each of the following:
Question 1.
The length of the longest rod that can be fitted in a cubical vessel of edge 10 cm long, is
(a) 10 cm
(b) 10\(\sqrt { 2 } \) cm
(c) 10\(\sqrt { 3 } \) cm
(d) 20 cm
Solution:
Edge of cuboid (a) = 10 cm
∴ Longest edge = \(\sqrt { 3 } \) a cm
= \(\sqrt { 3 } \) x 10 = 10\(\sqrt { 3 } \) cm (c)
Question 2.
Three equal cubes are placed adjacently in a row. The ratio of the total surface area of the resulting cuboid to that of the sum of the surface areas of three cubes, is
(a) 7 : 9
(b) 49 : 81
(c) 9 : 7
(d) 27 : 23
Solution:
Let a be the side of three equal cubes
∴ Surface area of 3 cubes
= 3 x 6a2 = 18a2
and length of so formed cuboid = 3a
Breadth = a
and height = a
∴ Surface area = 2(lb + bh + hl)
= 2[3a x a + a x a+a x 3a] = 2[3a2 + a2 + 3a2] = 2 x 7a2 = 14a2
∴ Ratio in the surface areas of cuboid and three cubes = 14a2 : 18a2= 7:9 (a)
Question 3.
If the length of a diagonal of a cube is 8 \(\sqrt { 3 } \) cm, then its surface area is
(a) 512 cm2
(b) 384 cm2
(c) 192 cm2
(d) 768 cm2
Solution:
Length of the diagonal of cube = 8 \(\sqrt { 3 } \) cm

Question 4.
If the volumes of two cubes are in the ratio 8:1, then the ratio of their edges is
(a) 8 : 1
(b) 2\(\sqrt { 2 } \) : 1
(c) 2 : 1
(d) none of these
Solution:
Let volume of first cube = 8x3
and of second cube = x3
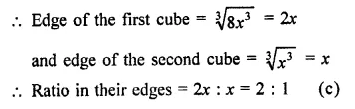
Question 5.
The volume of a cube whose surface area is 96 cm2, is
(a) 16\(\sqrt { 2 } \) cm3
(b) 32 cm3
(c) 64 cm3
(d) 216 cm3
Solution:
Surface area of a cube = 96 cm2
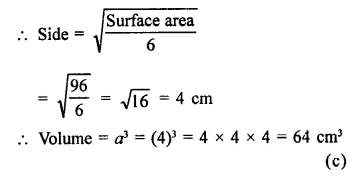
Question 6.
The length, width and height of a rectangular solid are in the ratio of 3 : 2 : 1. If the volume of the box is 48 cm3, the total surface area of the box is
(a) 27 cm2
(b) 32 cm2
(c) 44 cm2
(d) 88 cm2
Solution:
Ratio in the dimensions of a cuboid =3 : 2 : 1
Let length = 3x
Breadth = 2x
and height = x
Then volume = lbh = 3x x 2x x x = 6×3
∴ 6x3 = 48 ⇒ x3= \(\frac { 48 }{ 6 }\) = 8 = (2)3
∴ x = 2
∴ Length (l) = 3 x 2 = 6 cm
Breadth (b) = 2 x 2 = 4 cm
Height (h) = 1 x 2 = 2 cm
Now surface area = 2[lb + bh + hl]
= 2[6 x 4 + 4 x 2 + 2 x 6] cm2
= 2[24 + 8-+ 12] = 2 x 44 cm2
= 88 cm2 (d)
Question 7.
If the areas of the adjacent faces of a rectangular block are in the ratio 2:3:4 and its volume is 9000 cm3, then the length of the shortest edge is
(a) 30 cm
(b) 20 cm
(c) 15 cm
(d) 10 cm
Solution:
Ratio in the areas of three adjacent faces of a cuboid = 2 : 3 : 4
Volume = 9000 cm3
Let the area of faces be 2x, 3x, Ax and
Let a, b, and c be the dimensions of the cuboid, then
∴ 2x = ab, 3x = be, 4x = ca
∴ ab x be x ca = 2x x 3x x 4x
a2b2c2 = 24 x 3
But volume = abc = 9000 cm3
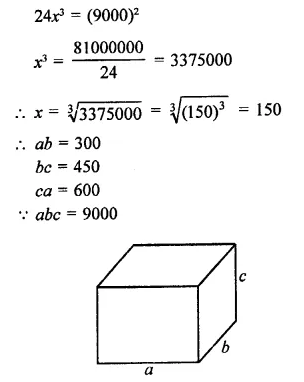
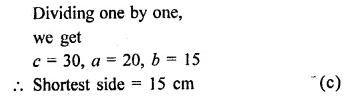
Question 8.
If each edge of a cube, of volume V, is doubled, then the volume of the new cube is
(a) 2V
(b) 4V
(c) 6V
(d) 8V
Solution:
Let a be the edge of a cube whose Volume = V
∴ a3 = V
By doubling the edge, we get 2a
Then volume = (2a)3 = 8a3
∴ Volume of new cube = 8a3 = 8V (d)
Question 9.
If each edge of a cuboid of surface area S is doubled, then surface area of the new cuboid is
(a) 2S
(b) 4S
(c) 6S
(d) 8S
Solution:
Let each edge of a cube = a
Then surface area = 6a2
∴ S = 6a2
Now doubling the edge, we get
New edge of a new cube = 2a
∴ Surface area = 6(2a)2
= 6 x 4a2 = 24a2
= 4 x 6a2 = 4S (b)
Question 10.
The area of the floor of a room is 15 m2. If its height is 4 m, then the volume of the air contained in the room is
(a) 60 dm3
(b) 600 dm3
(c) 6000 dm3
(d) 60000 dm3
Solution:
Area of a floor of a room = 15 m2
Height (h) = 4 m
∴ Volume of air in the room = Floor area x Height
= 15 m2 x 4 m = 60 m3
= 60 x 10 x 10 x 10 dm2 = 60000 dm2 (d)
Question 11.
The cost of constructing a wall 8 m long, 4 m high and 20 cm thick at the rate of ₹25 per m3 is
(a) ₹16
(b) ₹80
(c) ₹160
(d) ₹320
Solution:
Length of wall (l) = 8 m
Breadth (b) = 20 cm = \(\frac { 1 }{ 5 }\) m
Height (h) = 4 m

Question 12.
10 cubic metres clay in uniformaly spread on a land of area 10 acres. The rise in the level of the ground is
(a) 1 cm
(b) 10 cm
(c) 100 cm
(d) 1000 cm
Solution:
Volume of clay = 10 m3
Area of land = 10 acres
= 10 x 100 = 1000 m2
∴ Rise of level by spreading the clay
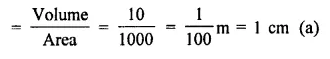
Question 13.
Volume of a cuboid is 12 cm3. The volume (in cm3) of a cuboid whose sides are double of the above cuboid is
(a) 24
(b) 48
(c) 72
(d) 96
Solution:
Volume of cuboid = 12 cm3
By doubling the sides of the cuboid the
volume will be = 12 cm3 x 2 x 2 x 2
= 96 cm3 (d)
Question 14.
If the sum of all the edges of a cube is 36 cm, then the volume (in cm3) of that cube is
(a) 9
(b) 27
(c) 219
(d) 729
Solution:
Sum of all edges of a cube = 36 cm
No. of edge of a cube are 12
∴ Length of its one edge = \(\frac { 36 }{ 12 }\) = 3 cm
Then volume = (edge)3 = (3)3 cm3
= 27 cm3 (b)
Question 15.
The number of cubes of side 3 cm that can be cut from a cuboid of dimensions 9 cm x 9 cm x 6 cm, is
(a) 9
(b) 10
(c) 18
(d) 20
Solution:
Dimensions of a cuboid = 9 cm x 9 cm x 6 cm
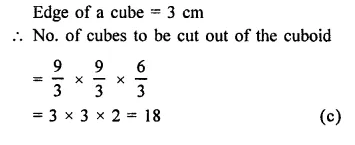
Question 16.
On a particular day, the rain fall recorded in a terrace 6 m long and 5 m broad is 15 cm. The quantity of water collected in the terrace is
(a) 300 litres
(b) 450 litres
(c) 3000 litres
(d) 4500 litres
Solution:
Dimension of a terrace = 6mx5m
Level of rain on it = 15 cm
∴ Volume of water collected on it
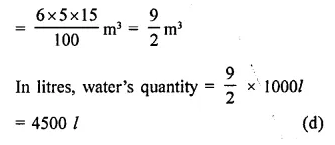
Question 17.
If A1, A2 and A3 denote the areas of three adjacent faces of a cuboid, then its volume is
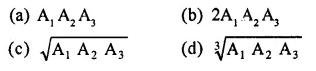
Solution:
Let l, b, h be the dimensions of the cuboid
∴ A1= lb, A2 = bh, A3 = hl
∴ A1 A2 A3 = lb.bh.hl = l2b2h2

Question 18.
If l is the length of a diagonal of a cube of volume V, then
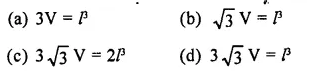
Solution:
Volume of a cube = V
and longest diagonal = l
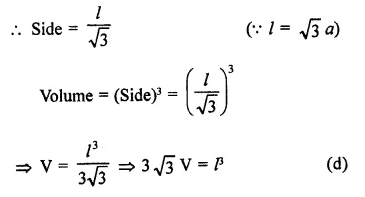
Question 19.
If V is the volume of a cuboid of dimensions x, y, z and A is its surface area, then \(\frac { A }{ V }\)
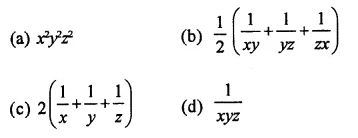
Solution:
A is surface area, V is volume and x, y and z are the dimensions
Then V = xyz
A = 2[xy + yz + zx]
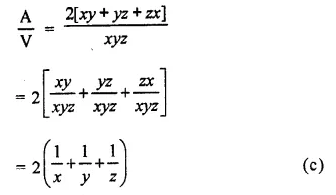
Question 20.
The sum of the length, breadth and depth of a cuboid is 19 cm and its diagonal is 5\(\sqrt { 5 } \) cm. Its surface area is
(a) 361 cm2
(b) 125 cm2
(c) 236 cm2
(d) 486 cm2
Solution:
Let x, y, z be the dimensions of a cuboid,
then x + y + z = 19 cm
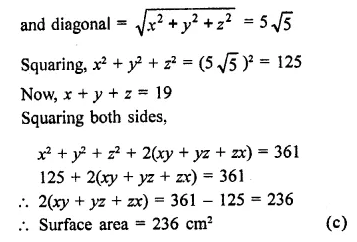
Question 21.
If each edge of a cube is increased by 50%, the percentage increase in its surface area is
(a) 50%
(b) 75%
(c) 100%
(d) 125%
Solution:
Let in first case, edge of a cube = a
Then surface area = 6a2
In second case, increase in side = 50%

Question 22.
A cube whose volume is 1/8 cubic centimeter is placed on top of a cube whose volume is. 1 cm3. The two ,cubes are then placed on top of a third cube whose volume is 8 cm3. The height of the stacked cubes is
(a) 3.5 cm
(b) 3 cm
(c) 7 cm
(d) none of these
Solution:
Volume of first cube = \(\frac { 1 }{ 2 }\) cm3
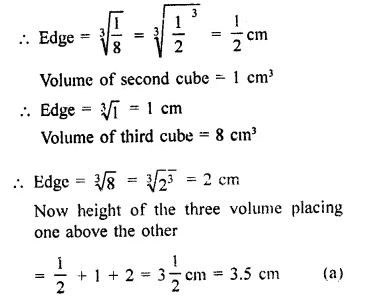
Hope given RD Sharma Class 9 Solutions Chapter 18 Surface Areas and Volume of a Cuboid and Cube MCQS are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.