RD Sharma Class 9 Solutions Chapter 18 Surface Areas and Volume of a Cuboid and Cube Ex 18.1
These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 18 Surface Areas and Volume of a Cuboid and Cube Ex 18.1
Other Exercises
- RD Sharma Class 9 Solutions Chapter 18 Surface Areas and Volume of a Cuboid and Cube Ex 18.1
- RD Sharma Class 9 Solutions Chapter 18 Surface Areas and Volume of a Cuboid and Cube Ex 18.2
- RD Sharma Class 9 Solutions Chapter 18 Surface Areas and Volume of a Cuboid and Cube VSAQS
- RD Sharma Class 9 Solutions Chapter 18 Surface Areas and Volume of a Cuboid and Cube MCQS
Question 1.
Find the lateral surface area and total surface area of a cuboid of length 80 cm, breadth 40 cm and height 20 cm.
Solution:
Length of cuboid (l) = 80 cm
Breadth (b) = 40 cm
Height (h) = 20 cm
(i) ∴ Lateral surface area = 2h(l + b)
= 2 x 20(80 + 40) cm²
= 40 x 120 = 4800 cm²
(ii) Total surface area = 2(lb + bh + hl)
= 2(80 x 40 + 40 x 20 + 20 x 80) cm²
= 2(3200 + 800 + 1600) cm²
= 5600 x 2 = 11200 cm²
Question 2.
Find the lateral surface area and total surface area of a cube of edge 10 cm.
Solution:
Edge of cube (a) = 10 cm
(i) ∴ Lateral surface area = 4a²
= 4 x (10)² = 4 x 100 cm²= 400 cm²
(ii) Total surface area = 6a² = 6 x(10)² cm²
= 6 x 100 = 600 cm²
Question 3.
Find the ratio of the total surface area and lateral surface area of a cube.
Solution:
Let a be the edge of the cube, then Total surface area = 6a2²
and lateral surface area = 4a²
Now ratio between total surface area and lateral surface area = 6a² : 4a² = 3 : 2
Question 4.
Mary wants to decorate her Christmas tree. She wants to place the tree on a wooden block covered with coloured paper with picture of Santa Claus on it. She must know the exact quantity of paper to buy for this purpose. If the box has length, breadth and height as 80 cm, 40 cm and 20 cm respectively. How many square sheets of paper of side 40 cm would she require? [NCERT]
Solution:
Length of box (l) = 80 cm
Breadth (b) = 40 cm
and height (h) = 20 cm
∴ Total surface area = 2(lb + bh + hl)
= 2[80 x 40 + 40 x 20 + 20 x 80] cm²
= 2[3200 + 800 + 1600] cm² = 2 x 5600 = 11200 cm²
Size of paper sheet = 40 cm
∴ Area of one sheet = (40 cm)² = 1600 cm²
∴ No. of sheets required for the box = 11200 = 1600 = 7 sheets
Question 5.
The length, breadth and height of a room are 5 m, 4 m and 3 m respectively. Find the cost of white washing the walls of the room and the ceiling at the rate of ₹7.50 m².
Solution:
Length of a room (l) = 5m
Breadth (b) = 4 m
and height (h) = 3 m
∴ Area of 4 walls = 2(l + b) x h
= 2(5 + 4) x 3 = 6 x 9 = 54 m²
and area of ceiling = l x b = 5 x 4 = 20 m²
∴ Total area = 54 + 20 = 74 m2
Rate of white washing = 7.50 per m²
∴ Total cost = ₹74 x 7.50 = ₹555
Question 6.
Three equal cubes are placed adjacently in a row. Find the ratio of total surface area of the new cuboid to that of the sum of the surface areas of the three cubes.
Solution:
Let each side of a cube = a cm
Then surface area = 6a² cm²
and surface area of 3 such cubes = 3 x 6a² = 18a² cm²
By placing three cubes side by side we get a cuboid whose,
Length (l) = a x 3 = 3a
Breadth (b) = a
Height (h) = a
∴ Total surface area = 2(lb + bh + hf)
= 2[3a x a+a x a+a x 3a] cm²
= 2[3a² + a² + 3a²] = 14 a²
∴ Ratio between their surface areas = 14a² : 18a² = 7 : 9
Question 7.
A 4 cm cube is cut into 1 cm cubes. Calculate the total surface area of all the small cubes.
Solution:
Side of cube = 4 cm
But cutting into 1 cm cubes, we get = 4 x 4 x 4 = 64
Now surface area of one cube = 6 x (1)²
= 6 x 1=6 cm²
and surface area of 64 cubes = 6 x 64 cm² = 384 cm²
Question 8.
The length of a hall is 18 m and the width 12 m. The sum of the areas of the floor and the flat roof is equal to the sum of the areas of the four walls. Find the height of the hall.
Solution:
Let h be the height of the room
Length (l) = 18 m
and width (b) = 12 m
Now surface area of floor and roof = 2 x lb = 2 x 18 x 12 m²
= 432 m²
and surface area of 4-walls = 2h (l + b)
= 2h(18 + 12) = 2 x 30h m² = 60h m²
∵ The surface are of 4-walls and area of floor and roof are equal
∴ 60h = 432
⇒ h = \(\frac { 432 }{ 60 }\) = \(\frac { 72 }{ 10 }\) m
∴ Height = 7.2m
Question 9.
Hameed has built a cubical water tank with lid for his house, with each other edge 1.5m long. He gets the outer surface of the tank excluding the base, covered with square tiles of side 25 cm. Find how much he would spend for the tiles, if the cost of tiles is ₹360 per dozen. [NCERT]
Solution:
Edge of cubical tank = 1.5 m
∴ Area of 4 walls = 4 (side)² = 4(1.5)² m² = 4 x 225 = 9 m²
Area of floor = (1.5)² = 2.25 m²
∴ Total surface area = 9 + 2.25 = 11.25 m²
Edge of square tile = 25 m = 0.25 m²
∴ Area of 1 tile = (0.25)2 = .0625 m²

Question 10.
Each edge of a cube is increased by 50%. Find the percentage increase in the surface area of the cube.
Solution:
Let edge of a cube = a
Total surface area = 6a2
By increasing edge at 50%,
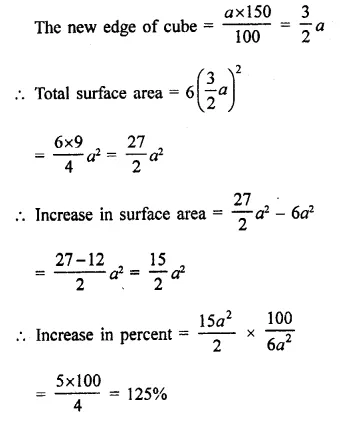
Question 11.
A closed iron tank 12 m long, 9 m wide and 4 m deep is to be made. Determine the cost of iron sheet used at the rate of ₹5 per metre sheet, sheet being 2 m wide.
Solution:
Length of iron tank (l) = 12 m
Breadth (b) = 9 m
Depth (h) = 4 cm

Question 12.
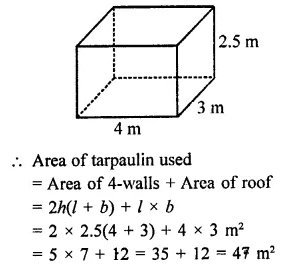
Ravish wanted to make a temporary shelter for his car by making a box-like structure with tarpaulin that covers all the four sides and the top of tire car (with the front face as a flap which can be rolled up). Assuming that the stitching margins are very small, and therefore negligible, how much tarpaulin would be required to make (he shelter of height 2.5 m with base dimensions 4 m x 3 m? [NCERT]
Solution:
Length of base (l) = 4m
Breadth (b) = 3 m
Height (h) = 2.5 m
Question 13.
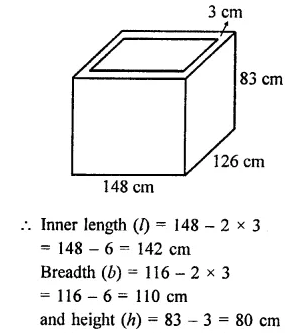
An open box is made of wood 3 cm thick. Its external length, breadth and height are 1.48 m, 1.16 m and 8.3 dm. Find the cost of painting the inner surface of ₹50 per sq. metre.
Solution:
Length of open wood box (L) = 1.48 m = 148 cm
Breadth (B) = 1.16 m = 116 cm
and height (H) = 8.3 dm = 83 cm
Thickness of wood = 3 cm

Question 14.
The dimensions of a room are 12.5 m by 9 m by 7 m. There are 2 doors and 4 windows in the room; each door measures 2.5 m by 1.2 m and each window 1.5 m by 1 m. Find the cost of painting the walls at ₹3.50 per square metre.
Solution:
Length of room (l) = 12.5 m
Breadth (b) = 9 m
and height (h) = 7 m
∴ Total area of walls = 2h(l + b)
= 2 x 7[12.5 + 9] = 14 x 21.5 m² = 301 m²
Area of 2 doors of 2.5 m x 1.2 m
= 2 x 2.5 x 1.2 m² = 6 m²
and area of 4 window of 1.5 m x 1 m
= 4 x 1.5 x 1 = 6 m²
∴ Remaining area of walls = 301 – (6 + 6)
= 301 – 12 = 289 m²
Rate of painting the walls = ₹3.50 per m²
∴ Total cost = 289 x 3.50 = ₹1011.50
Question 15.
The paint in a certain container is sufficient to paint on area equal to 9.375 m2. How many bricks of dimension 22.5 cm x 10 cm x 7.5 cm can be painted out of this container? [NCERT]
Solution:
Area of place for painting = 9.375 m²
Dimension of one brick = 22.5 cm x 10 cm x 7.5 cm
∴ Surface area of one bricks = 2 (lb + bh + hl)
= 2[22.5 x 10 + 10 x 7.5 + 7.5 x 22.5] cm2
= 2[225 + 75 + 168.75]
= 2 x 468.75 cm² = 937.5 cm²
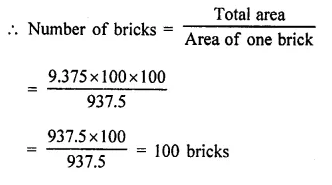
Question 16.
The dimensions of a rectangular box are in the ratio of 2 : 3 : 4 and the difference between the cost of covering it with sheet of paper at the rates of ₹8 and ₹9.50 per m2 is ₹1248. Find the dimensions of the box.
Solution:
Ratio in the dimensions of a cuboidal box = 2 : 3 : 4
Let length (l) = 4x
Breadth (b) = 3.v
and height (h) = 2x
∴ Total surface area = 2 [lb + bh + hl]

Question 17.
The cost of preparing the walls of a room 12 m long at the rate of ₹1.35 per square metre is ₹340.20 and the cost of matting the floor at 85 paise per square metre is ₹91.80. Find the height of the room.
Solution:
Cost of preparing walls of a room = ₹340.20

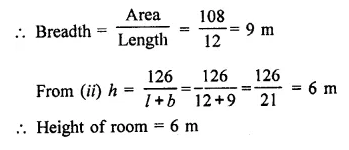
Question 18.
The length and breadth of a hall are in the ratio 4 : 3 and its height is 5.5 metres. The cost of decorating its walls (including doors and windows) at ₹6.60 per square metre is ₹5082. Find the length and breadth of the room
Solution:
Ratio in length and breadth = 4:3
and height (h) = 5.5 m
Cost of decorating the walls of a room including doors and windows = ₹5082
Rate = ₹6.60 per m²

Question 19.
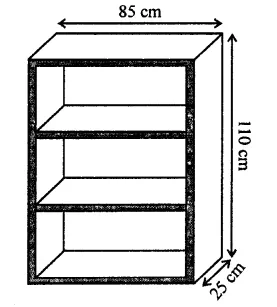
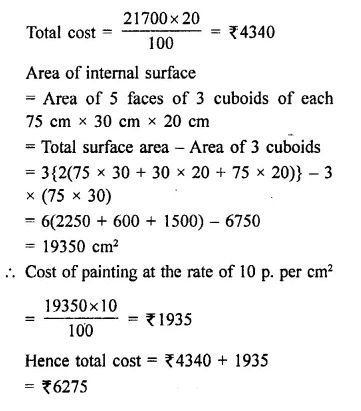
A wooden bookshelf has external dimensions as follows: Height =110 cm, Depth = 25 cm, Breadth = 85 cm (see figure). The thickness of the plank is 5 cm everywhere. The external faces are to be polished and the inner faces are to be painted. If the rate of polishing is 20 paise per cm2 and the rate of painting is 10 paise per cm2. Find the total expenses required for polishing and painting the surface of the bookshelf. [NCERT]
Solution:
Length (l) = 85 cm
Breadth (b) = 25 cm
and height (h) = 110 cm
Thickness of plank = 5 cm
Surface area to be polished
= [(100 x 85) + 2 (110 x 25) + 2 (85 x 25) + 2 (110 x 5) + 4 (75 x 5)]
= (9350 + 5500 + 4250 + 1100 + 1500) cm² = 21700 cm²
Hope given RD Sharma Class 9 Solutions Chapter 18 Surface Areas and Volume of a Cuboid and Cube Ex 18.1 are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.