RD Sharma Class 9 Solutions Chapter 19 Surface Areas and Volume of a Circular Cylinder MCQS
These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 19 Surface Areas and Volume of a Circular Cylinder MCQS
Other Exercises
- RD Sharma Class 9 Solutions Chapter 19 Surface Areas and Volume of a Circular Cylinder Ex 19.1
- RD Sharma Class 9 Solutions Chapter 19 Surface Areas and Volume of a Circular Cylinder Ex 19.2
- RD Sharma Class 9 Solutions Chapter 19 Surface Areas and Volume of a Circular Cylinder VSAQS
- RD Sharma Class 9 Solutions Chapter 19 Surface Areas and Volume of a Circular Cylinder MCQS
Mark correct alternative in each of the following:
Question 1.
In a cylinder, if radius is doubled and height is halved, curved surface area will be
(a) halved
(b) doubled
(c) same
(d) four times
Solution:
Let radius of the first cylinder (r1) = r
and height (h1) = h
Surface area = 2πrh
If radius is doubled and height is halved
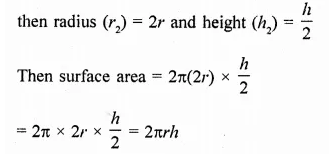
∴ Their surface area remain same (c)
Question 2.
Two cylindrical jars have their diameters in the ratio 3:1, but height 1:3. Then the ratio of their volumes is
(a) 1 : 4
(b) 1 : 3
(c) 3 : 1
(d) 2 : 5
Solution:
Sol. Ratio in the diameters of two cylinder = 3:1
and ratio in their heights = 1:3
Let radius of the first cylinder (r1) = 3x
and radius of second (r2) = x
and height of the first (h1) = y
and height of the second (h2) = 3y
Now volume of the first cylinder = πr2h
= π(3x)2 x y = 9πx2y
and of second cylinder = π(x2) (3y)
∴ Ratio between then = 9πx2y : 3πx2y
= 3 : 1 (c)
Question 3.
The number of surfaces in right cylinder is
(a) 1
(b) 2
(c) 3
(d) 4
Solution:
The number of surfaces of a right cylinder is three. (c)
Question 4.
Vertical cross-section of a right circular cylinder is always a
(a) square
(b) rectangle
(c) rhombus
(d) trapezium
Solution:
The vertical cross-section of a right circular cylinder is always a rectangle. (b)
Question 5.
If r is the radius and h is height of the cylinder the volume will be
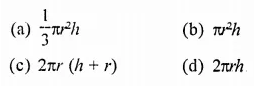
Solution:
Volume of a cylinder = πr2h (b)
Question 6.
The number of surfaces of a hollow cylindrical object is
(a) 1
(b) 2
(c) 3
(d) 4
Solution:
The number of surfaces of a hollow cylindrical object is 4. (d)
Question 7.
If the radius of a cylinder is doubled and the height remains same, the volume will be
(a) doubled
(b) halved
(c) same
(d) four times
Solution:
If r be the radius and h be the height, then volume = πr2h
If radius is doubled and height remain same,
the volume will be
= π(2r)2h = π x 4r2h
= 4πr2h = 4 x Volume
The volume is four times (d)
Question 8.
If the height of a cylinder is doubled and radius remains the same, then volume will be
(a) doubled
(b) halved
(c) same
(d) four times
Solution:
If r be the radius and h be the height, then volume of a cylinder = πr2h
If height is doubled and radius remain same, then volume = πr2(2h) = 2πr2h
∴ Its doubled (a)
Question 9.
In a cylinder, if radius is halved and height is doubled, the volume will be
(a) same
(b) doubled
(c) halved
(d) four times
Solution:
Let r be radius and h be height, then Volume = πr2h
If radius is halved and height is doubled
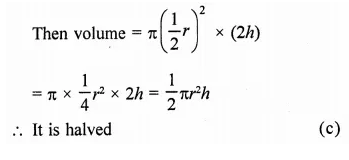
Question 10.
If the diameter of the base of a closed right circular cylinder be equal to its height h, then its whole surface area is
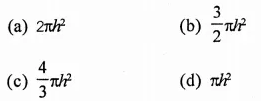
Solution:
Let diameter of the base of a cylinder (r) = h
Then its height (h) = h
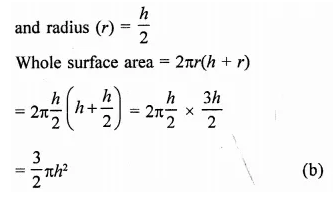
Question 11.
A right circular cylindrical tunnel of diameter 2 m and length 40 m is to be constructed from a sheet of iron. The area of the iron sheet required in m2, is
(a) 40π
(b) 80π
(c) 160π
(d) 200π
Solution:
Diameter of a cylindrical tunnel = 2 m
∴ Radius (r) = \(\frac { 2 }{ 2 }\) = 1m
and length (h) = 40 m
Curved surfae area = 2πrh = 2 x π x 1 x 40 = 80π (b)
Question 12.
Two circular cylinders of equal volume have their heights in the ratio 1 : 2. Ratio of their radii is

Solution:
Let r1 and h1 be the radius and height of the
first cylinder, then
Volume = πr12h1
Similarly r1 and h2 are the radius and height of the second cylinder
∴ Volume = πr2h2
But their volumes are equal,
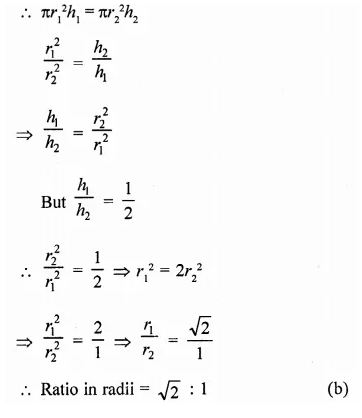
Question 13.
The radius of a wire is decreased to one- third. If volume remains the same, the length will become
(a) 3 times
(b) 6 times
(c) 9 times
(d) 27 times
Solution:
In the first case, r and h1, be the radius and height of the cylindrical wire
∴ Volume = πr2h1 …(i)
In second case, radius is decreased to one third
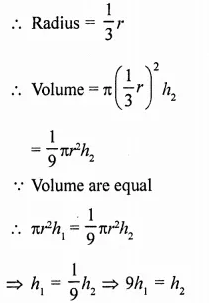
∴ In second case height is 9 times (c)
Question 14.
If the height of a cylinder is doubled, by what number must the radius of the base be multiplied so that the resulting cylinder has the same volume as the original cylinder?
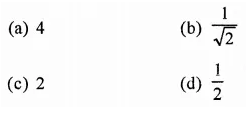
Solution:
Let r be the radius and h be the height then volume = πr2h
If height is doubled and volume is same and let x be radius then πr2h = π(x)2 x 2h
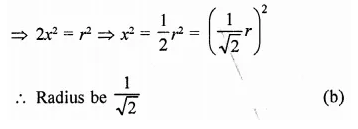
Question 15.
The volume of a cylinder of radius r is 1/4 of the volume of a rectangular box with a square base of side length x. If the cylinder and the box have equal heights, what is r in terms of x?
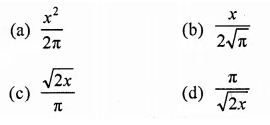
Solution:
Let r be the radius and h be the height, then volume = πr2h
This volume is \(\frac { 1 }{ 4 }\) of the volume of a rectangular box
∴ Volume of box = 4πr2h
Let side of base of box = x and height h,
then volume = x2h
∴ 4πr2h = x2h
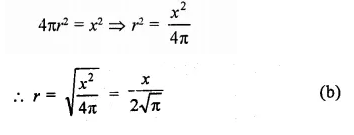
Question 16.
The height ft of a cylinder equals the circumference of the cylinder. In terms of ft, what is the volume of the cylinder?

Solution:
In a cylinder,
h = circumference of the cylinder
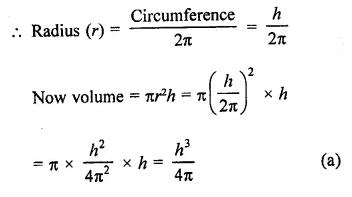
Question 17.
A cylinder with radius r and height ft is closed on the top and bottom. Which of the following expressions represents the total surface area of this cylinder?
(a) 2πr(r + h)
(b) πr(r + 2h)
(c) πr(2r + h)
(d) 2πr2 + h
Solution:
r is the radius of the base and ft is the height of a closed cylinder
Then total surface area = 2πr(r + h ) (a)
Question 18.
The height of sand in a cylindrical-shaped can drops 3 inches when 1 cubic foot of sand is poured out. What is the diameter, in inches, of the cylinder?
Solution:
Let h be the height and d be the diameter of a cylinder, then
Question 19.
Two steel sheets each of length a1 and breadth a2 are used to prepare the surfaces of two right circular cylinders – one having volume v1 and height a2 and other having volume v2 and height a1. Then,
Solution:
Length of each sheet = a1
and breadth = a2
Volume of cylinder = πr2h
In first case,
v1 is volume and a2 is the height
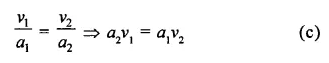
Question 20.
The altitude of a circualr cylinder is increased six times and the base area is decreased to one-ninth of its value. The factor by which the lateral surface of the cylinder increases, is

Solution:
In first case,
Let r be the radius and h be the height of the cylinder. Then,
∴ Lateral surface area = 2πrh
In second case,

Hope given RD Sharma Class 9 Solutions Chapter 19 Surface Areas and Volume of a Circular Cylinder MCQS are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.