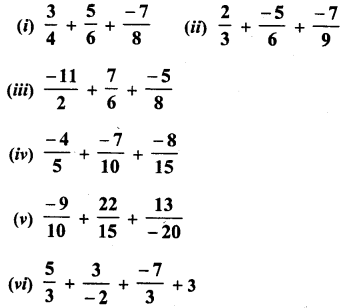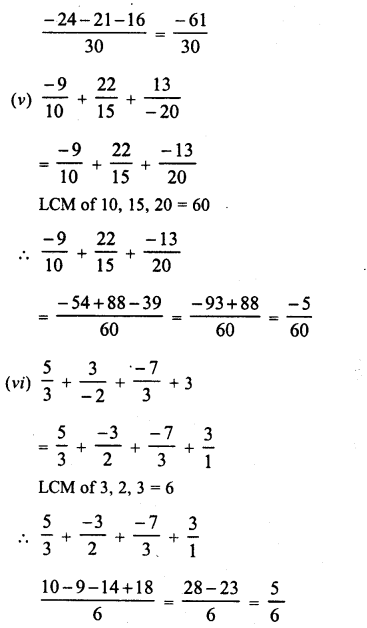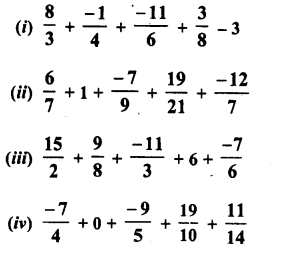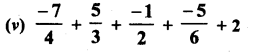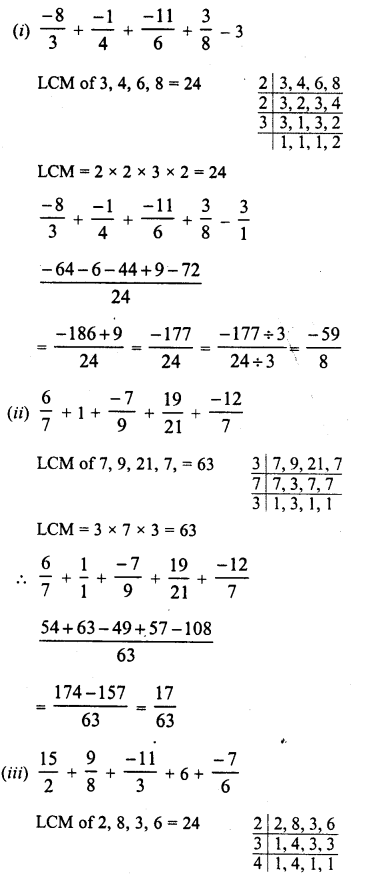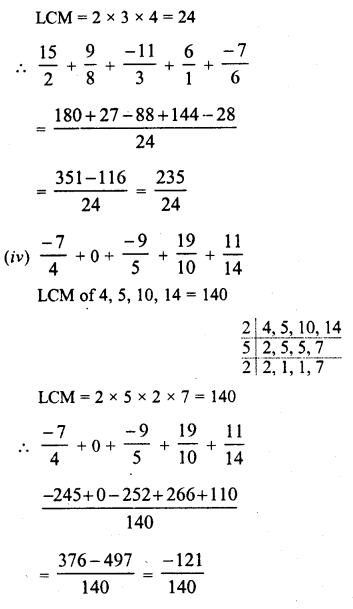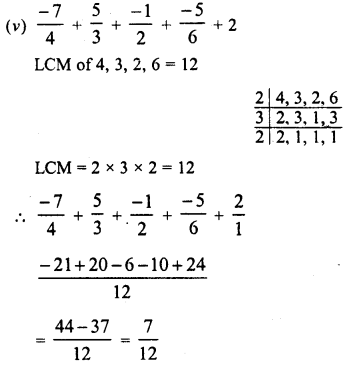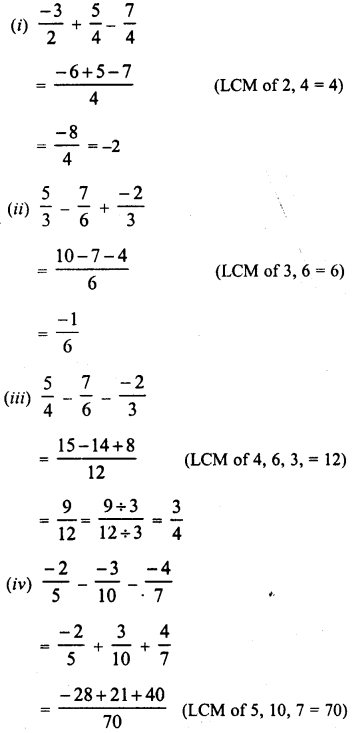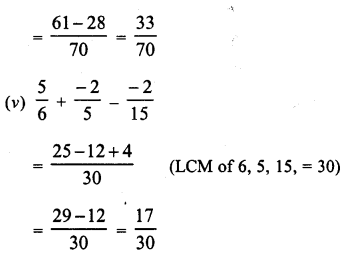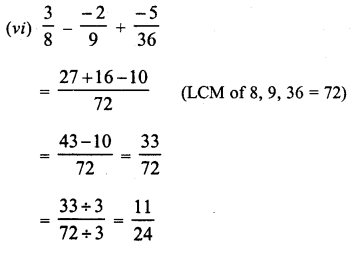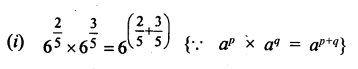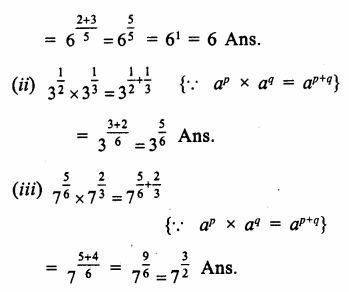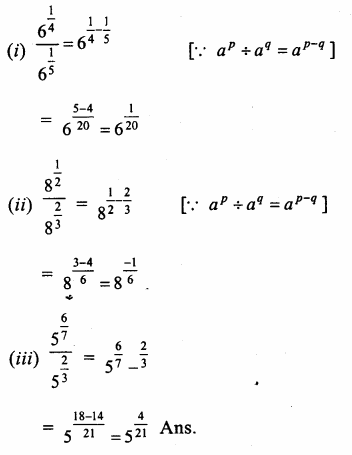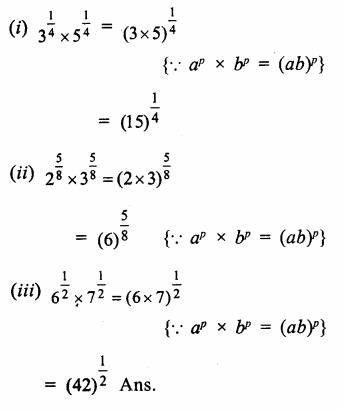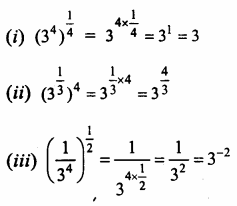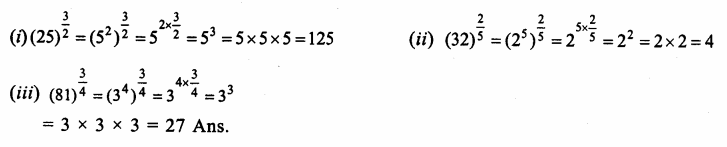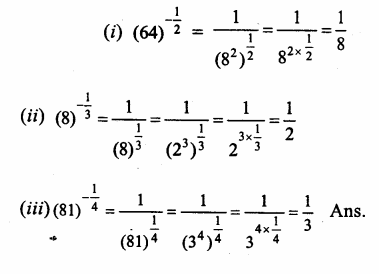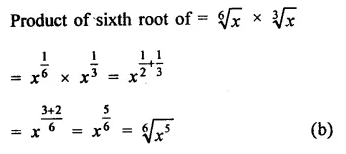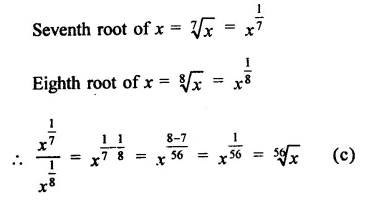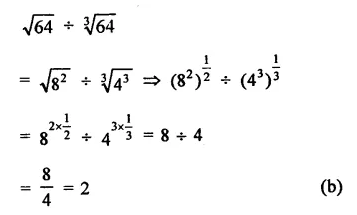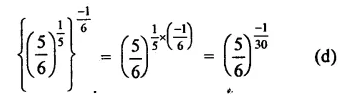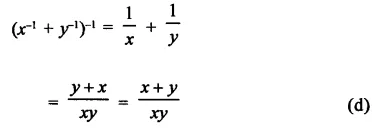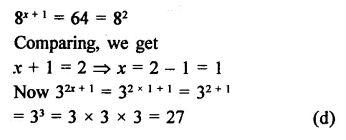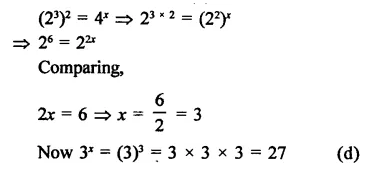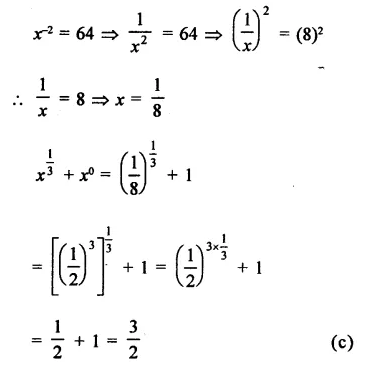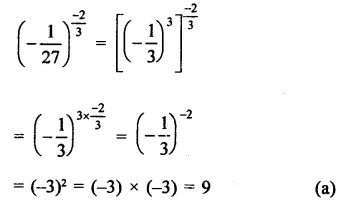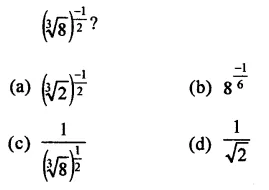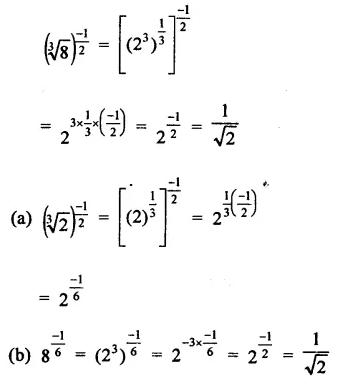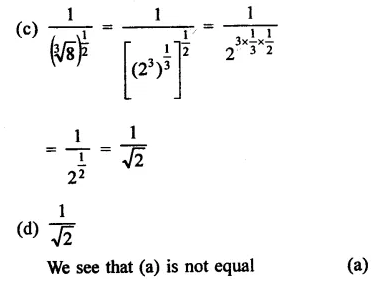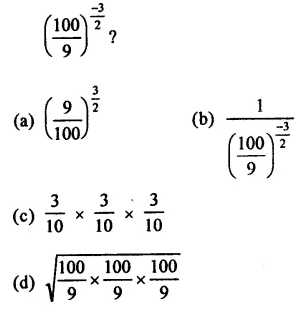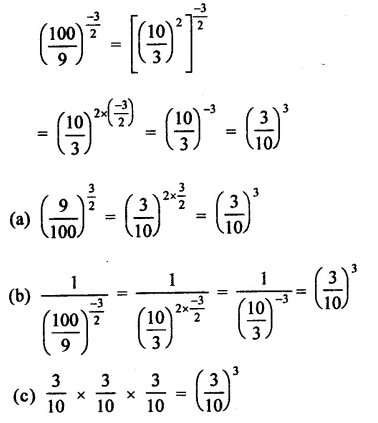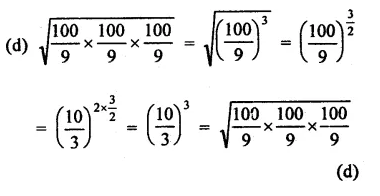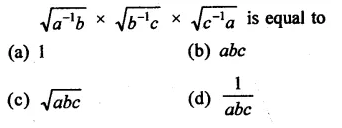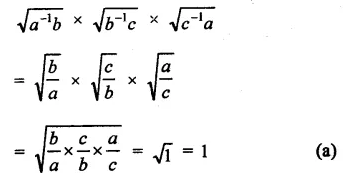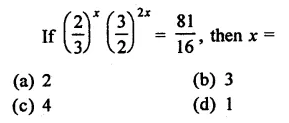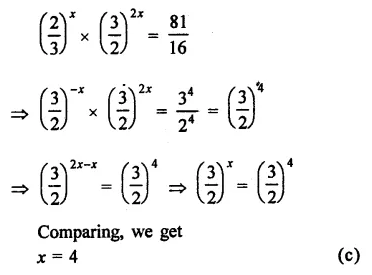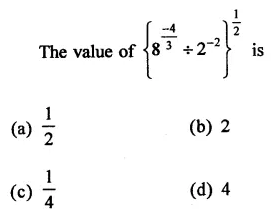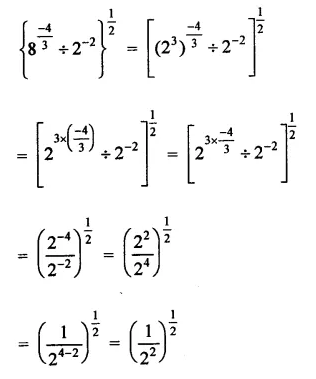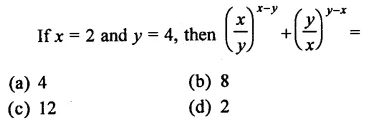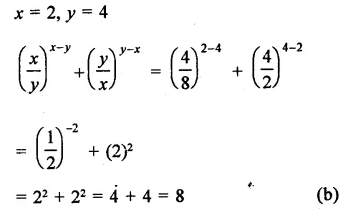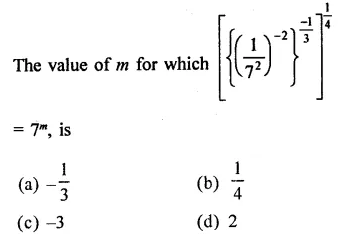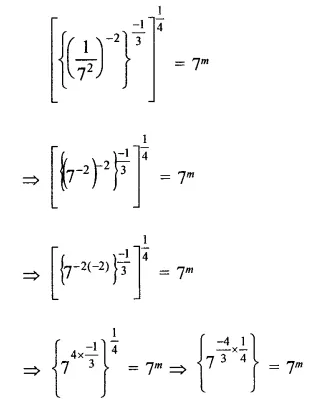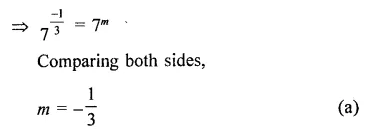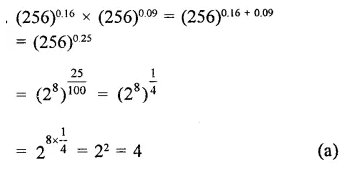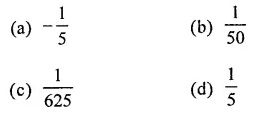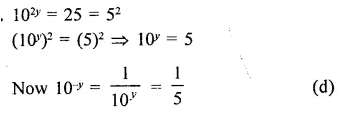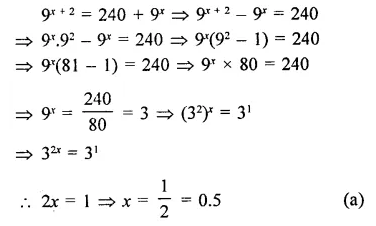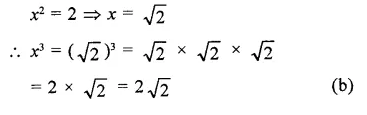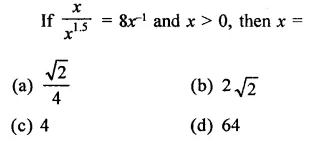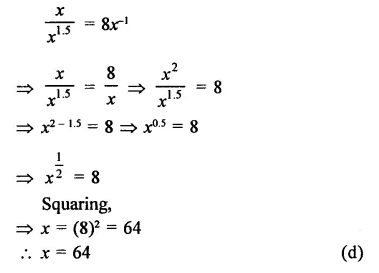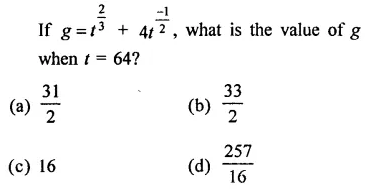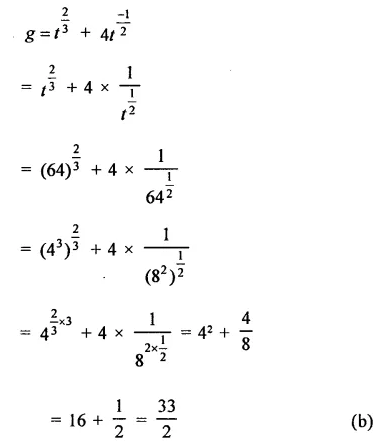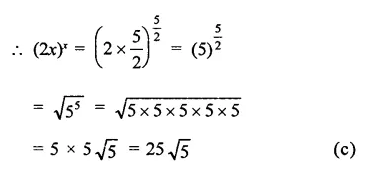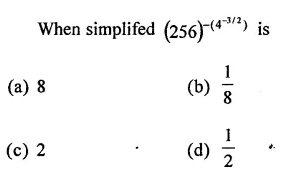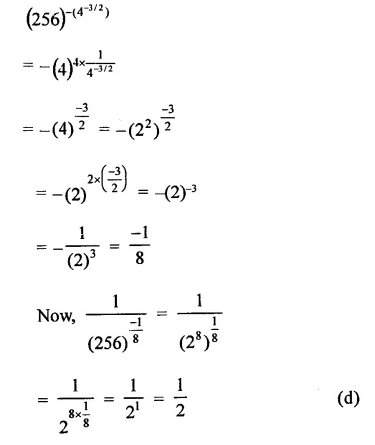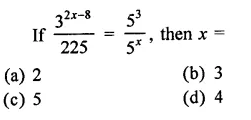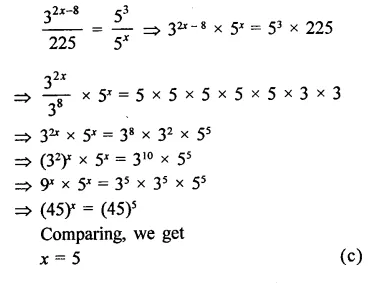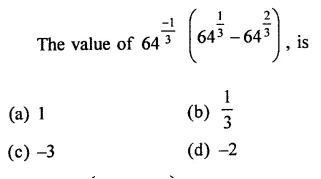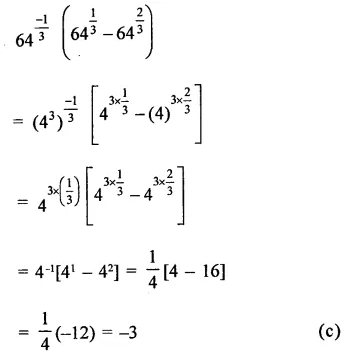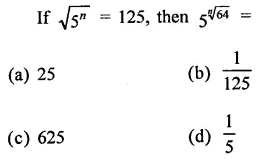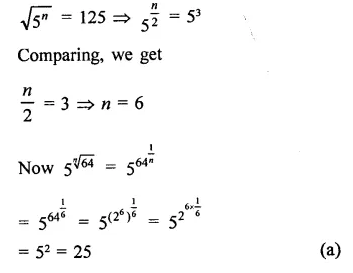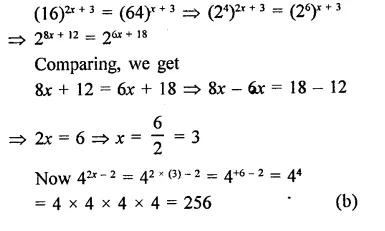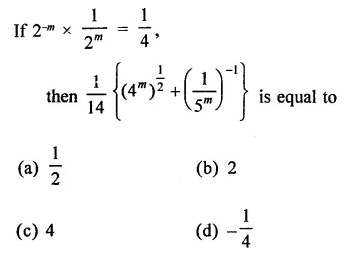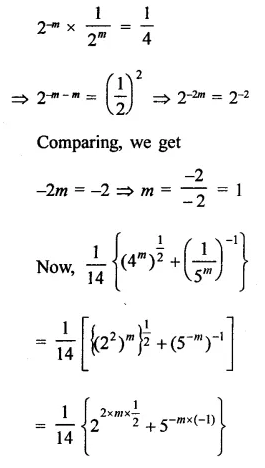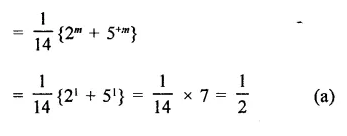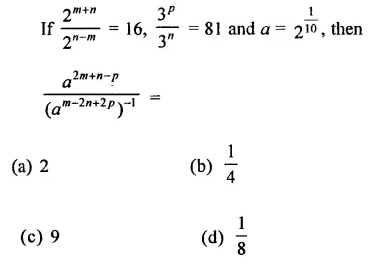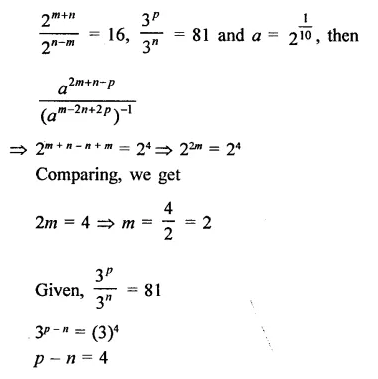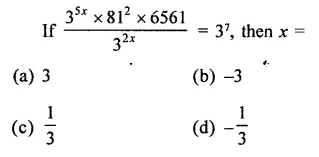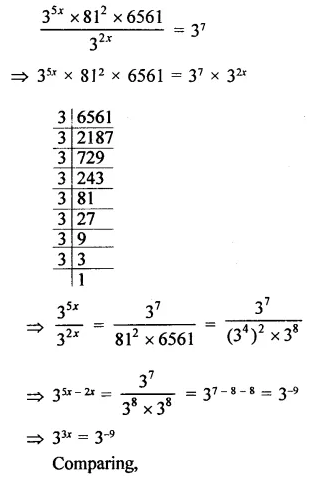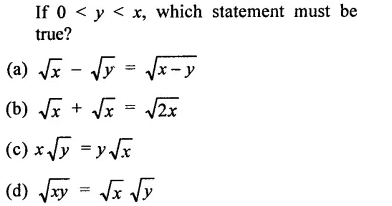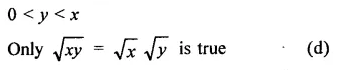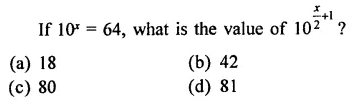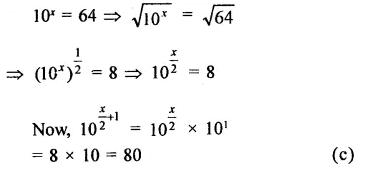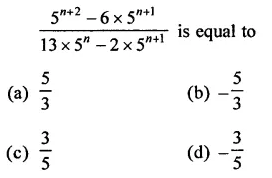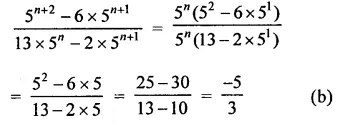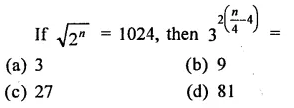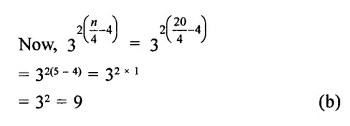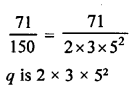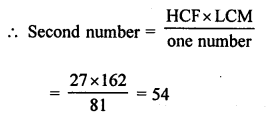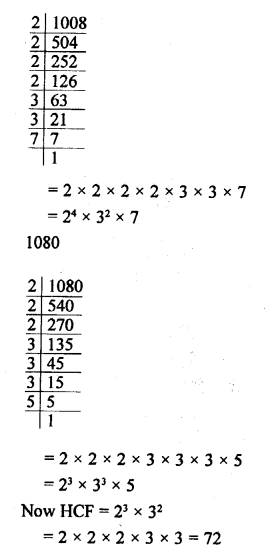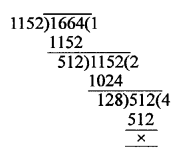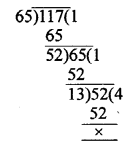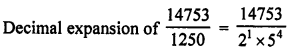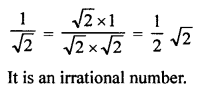Prasanna

RS Aggarwal Class 9 Solutions Chapter 1 Real Numbers Ex 1F

These Solutions are part of RS Aggarwal Solutions Class 9. Here we have given RS Aggarwal Solutions Class 9 Chapter 1 Real Numbers Ex 1F.

Other Exercises

• RS Aggarwal Solutions Class 9 Chapter 1 Real Numbers Ex 1A
• RS Aggarwal Solutions Class 9 Chapter 1 Real Numbers Ex 1B
• RS Aggarwal Solutions Class 9 Chapter 1 Real Numbers Ex 1C
• RS Aggarwal Solutions Class 9 Chapter 1 Real Numbers Ex 1D
• RS Aggarwal Solutions Class 9 Chapter 1 Real Numbers Ex 1E
• RS Aggarwal Solutions Class 9 Chapter 1 Real Numbers Ex 1F

Question 1.
Solution:
We know that
a^p x a^q = a^p+q
∴ Therefore

Question 2.
Solution:
We know that
a^p ÷ a^q = a^p-q
Therefore

Question 3.
Solution:
We know that
a^p x b^p = (ab)^p
Therefore

Question 4.
Solution:
We know that
(a^p)^q =a^pq

Question 5.
Solution:

Question 6.
Solution:

Question 7.
Solution:

Hope given RS Aggarwal Solutions Class 9 Chapter 1 Real Numbers Ex 1F are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 10 Solutions Chapter 1 Real Numbers Test Yourself

These Solutions are part of RS Aggarwal Solutions Class 10. Here we have given RS Aggarwal Solutions Class 10 Chapter 1 Real Numbers Test Yourself.

Other Exercises

• RS Aggarwal Solutions Class 10 Chapter 1 Real Numbers Ex 1A
• RS Aggarwal Solutions Class 10 Chapter 1 Real Numbers Ex 1B
• RS Aggarwal Solutions Class 10 Chapter 1 Real Numbers Ex 1C
• RS Aggarwal Solutions Class 10 Chapter 1 Real Numbers Ex 1D
• RS Aggarwal Solutions Class 10 Chapter 1 Real Numbers Ex 1E
• RS Aggarwal Solutions Class 10 Chapter 1 Real Numbers MCQs
• RS Aggarwal Solutions Class 10 Chapter 1 Real Numbers Test Yourself

Question 1.
Solution:
(b)

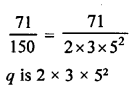
Its decimal will be nonterminating repeating decimal.

Question 2.
Solution:
(b) \(\frac { p }{ q }\) is terminating decimal if q = 2^m x 5ⁿ
Now, 91 = 7 x 13, 45 = 3² x 5
80 = 2⁴ x 5, 42 = 2 x 3 x 7
80 is of the form 2^m x 5ⁿ
\(\frac { 19 }{ 80 }\) is terminating decimal expansion,

Question 3.
Solution:
(b) Divisor = 9 and remainder = 7
Let b be the divisor, then
n = 9b + 7
Multiplying both sides by 3 and subtracting 1.
3n – 1 = 3(9b + 7) – 1
3n – 1 = 27b + 21 – 1
3n – 1 = 9(3b) + 9 x 2 + 2
3n – 1 = 9(3b + 2) + 2
Remainder = 2

Question 4.
Solution:
(b) \(0.\bar { 68 }\) + \(0.\bar { 73 }\)
0.686868 ……… + 0.737373……
= 1.424241 = \(1.\bar { 42 }\)

Short-Answer Questions (2 marks)
Question 5.
Solution:
4ⁿ, n ∈ N
4¹ = 4
4² = 4 x 4 = 16
4³ = 4 x 4 x 4 = 64
4⁴ = 4 x 4 x 4 x 4 = 256
4⁵ = 4 x 4 x 4 x 4 x 4 = 1024
We see that value of 4ⁿ, ends with 4 or 6 only.
Hence, the value of 4ⁿ, n ∈ N, never ends with 0.

Question 6.
Solution:
HCF of two numbers = 27 and LCM =162
One number = 81

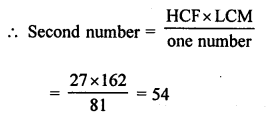
Question 7.
Solution:
\(\frac { 17 }{ 30 }\) = \(\frac { 17 }{ 2 x 3 x 5 }\)
Here, q is in the form of 2^m x 5ⁿ
It is not terminating decimal.

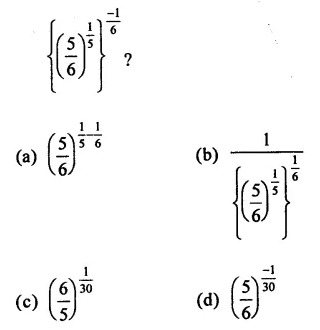
Question 8.
Solution:

Question 9.
Solution:

Question 10.
Solution:
Let (2 + √3) is rational and 2 is rational.
Difference of them is also rational.
=> (2 + √3) – 2 = 2 + √3 – 2
= √3 is rational
But it contradicts the fact.
(2 + √3) is irrational.

Short-Answer Questions (3 marks)
Question 11.
Solution:
HCF of 12, 15, 18, 27
12 = 2 x 2 x 3 = 2² x 3
15 = 3 x 5
18 = 2 x 3 x 3 = 2 x 3²
27 = 3 x 3 x 3 = 3³
Now, HCF = 3
and LCM = 2² x 3³ x 5 =2 x 2 x 3 x 3 x 3 x 5
= 4 x 27 x 5 = 540

Question 12.
Solution:
Let 2 + √3 and 2 – √3 are two irrational number.
Sum = 2 + √3 + 2 – √3 = 4 which is a rational.

Question 13.
Solution:
4620

Question 14.
Solution:
1008

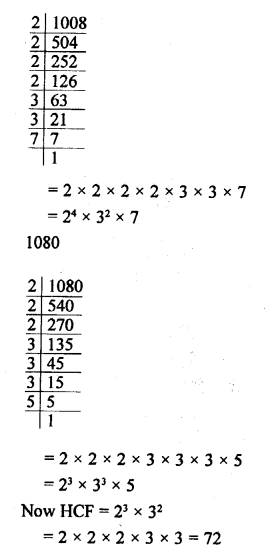
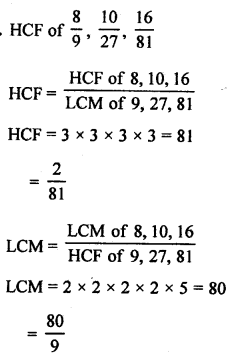
Question 15.
Solution:

Question 16.
Solution:
Give numbers are 546 and 764 and remainders are 6 and 8 respectively.
Remaining number 546 – 6 = 540
and 764 – 8 = 756
Now, required largest number = HCF of 540 and 756 = 108

Long-Answer Questions (4 marks)
Question 17.
Solution:
Let √3 is a rational number.
Let √3 = \(\frac { p }{ q }\) where p and q are integers and have no common factor, other than 1 and q ≠ 0
Squaring both sides.
3 = \(\frac { { p }^{ 2 } }{ { q }^{ 2 } }\) => 3q² – p²
=> 3 divides p²
=> 3 divides p
Let p = 3c for some integer c
3q² = 9c² => q² – 3c²
=> 3 divides q² (3 divides 3c²)
=> 3 divides q
3 is common factors of p and q
But it contradicts the fact that p and q have
no common factors and also contradicts that √3 is a rational number.
Hence, √3 is irrational number.

Question 18.
Solution:
Let n be an arbitrary odd positive integer on dividing n by 4, let m be the quotient and r be the remainder.
By Euclid’s division lemma,
n = 4q + r where 0 ≤ r < 4
n = 4q or (4q + 1) or (4q + 2) or (4q + 3)
Clearly, 4q and (4q + 2) are even number
since n is odd.
n ≠ 4q and n ≠ (4q + 2)
n = (4 q + 1) or (4q + 3) for same integer n
Hence, any positive odd integer of the form 4q + 1 or 4q + 3 for some integer q.

Question 19.
Solution:
On dividing n by 3, let q be the quotient and r be the remainder, then
n = 3q + r where 0 ≤ r < 3 => n = 3q + r where r = 0, 1 or 2
n = 3q or n = 3q + 1 or n = 3q + 2
(i) Case (I)
If n = 3q then n is divisible by 3
(ii) Case (II)
If n = (3q + 1) then n + 2 = 3q + 3 = 3q (q + 1) which is divisible by 3
In this case, n + 2 is divisible by 3
(iii) Case (III)
If n = (3q + 2) then n + 1 (n + 1) = 3q + 3 = 3(q + 1) which also divisible by 3
In this case, (n + 1) is divisible by 3
Hence, one and only one out of n, (n + 1) and (n + 2) is divisible by 3.

Question 20.
Solution:
Let (4 + 3√2) is rational number and 4 is also a rational number.
Difference of two rational numbers is also a rational number.
4 + 3√2 – 4 = 3√2 is a rational number
Product of two rational numbers is rational
3 is rational and √2 is rational
But it contradicts the fact
√2 is irrational
Hence, (4 + 3√2 ) is irrational.

Hope given RS Aggarwal Solutions Class 10 Chapter 1 Real Numbers Test Yourself  are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 10 Solutions Chapter 1 Real Numbers MCQS

These Solutions are part of RS Aggarwal Solutions Class 10. Here we have given RS Aggarwal Solutions Class 10 Chapter 1 Real Numbers MCQS.

Other Exercises

• RS Aggarwal Solutions Class 10 Chapter 1 Real Numbers Ex 1A
• RS Aggarwal Solutions Class 10 Chapter 1 Real Numbers Ex 1B
• RS Aggarwal Solutions Class 10 Chapter 1 Real Numbers Ex 1C
• RS Aggarwal Solutions Class 10 Chapter 1 Real Numbers Ex 1D
• RS Aggarwal Solutions Class 10 Chapter 1 Real Numbers Ex 1E
• RS Aggarwal Solutions Class 10 Chapter 1 Real Numbers MCQs
• RS Aggarwal Solutions Class 10 Chapter 1 Real Numbers Test Yourself

Choose the correct answer in each of the following questions.
Question 1.
Solution:
(b) We know that HCF of two co-prime number is 1
HCF of 14, 35 is 7
HCF of 18, 25 is 1
HCF of 31, 93 is 31
HCF of 32, 60 is 4
Required co-prime number is (18, 25)

Question 2.
Solution:
(b) a = (2² x 3³ x 5⁴), b = (2³ x 3² x 5)
HCF = 2² x 3² x 5 = 2 x 2 x 3 x 3 x 5 = 180

Question 3.
Solution:
(c) HCF of 2³ x 3² x 5, 2² x 3³ x 5², 2⁴ x 3 x 5³ x 7
HCF = 2² x 3 x 5 = 2 x 2 x 3 x 5 = 60

Question 4.
Solution:
(d) LCM of 2³ x 3 x 5, 2⁴ x 5 x 7 = 2⁴ x 3 x 5 x 7
=2 x 2 x 2 x 2 x 3 x 5 x 7
= 1680

Question 5.
Solution:
(d) HCF of two numbers = 27
LCM = 162
One number = 54

Question 6.
Solution:
(c) Product of two numbers = 1600
HCF = 5

Question 7.
Solution:
(c) Largest number that divides each one of 1152 and 1664
HCF of 1152 and 1664 =128

Question 8.
Solution:
(a) Largest number that divides 70 and 125 leaving remainders as 5 and 8 respectively.
Required number = 70 – 5 = 65
and 125 – 8= 117
HCF of 65, 117 = 13

Question 9.
Solution:
(b) Largest number that divides 245 and 1029 leaving remainder as 5 in each case. .
Required number = 245 – 5 = 240 and 1029 – 5 = 1024
Now, HCF of 240 and 1020 = 16

Question 10.
Solution:
(d)

Question 11.
Solution:
(c) In a = bq + r
r must satisfy i.e. 0 ≤ r < b

Question 12.
Solution:
(d) Let the given number when divided by 143 gives q as quotient and 31 as remainder.
Number = 143q + 31
= (13 x 11) q + 31
= 13 x 11 q+ 13 x 2 + 5
= 13 (110 + 2) + 5
The number where divided by 73, gives 5 as remainder.

Question 13.
Solution:
(d) 3.141141114… is irrational because it is non terminating non-repeating.

Question 14.
Solution:
(c) π is an irrational number.

Question 15.
Solution:
(b) \(2.\bar { 35 }\) is a rational number as it is non-terminating repeating decimal.

Question 16.
Solution:
(c) 2.13113111311113… is an irrational number.
It is non-terminating non-repeating decimal.

Question 17.
Solution:
(b) 3.24636363…
= \(3.24\bar { 63 }\)
It is non-terminating repeating decimal.
It is a rational number.

Question 18.
Solution:
(c) \(\frac { 2027 }{ 625 }\) = \(\frac { 2027 }{ { 5 }^{ 4 } }\) is a rational because it has terminating decimal as q = 5⁴ which is in form of 2^m x 5ⁿ.

Question 19.
Solution:
(b)

Question 20.
Solution:
(d)

Question 21.
Solution:
(b) 1.732 is a rational number.
As it is terminating decimal.

Question 22.
Solution:
(a) Least prime factor of a positive integer a is 3 and b is 5
2 is neither a factor of a nor of b
a and b are odd
Then (a + b) = even
(Sum of two odd numbers is even)
(a + b) is divisible by 2
Which is the least prime factor.

Question 23.
Solution:
(b) √2 is an irrational number.

Question 24.
Solution:
(c)

Question 25.
Solution:
(c) 2 + √2 is an irrational number as sum of a rational and an irrational is an irrational

Question 26.
Solution:
(c) LCM of 1 to 10 = 2 x 2 x 2 x 3 x 3 x 5 x 7 = 2520

Hope given RS Aggarwal Solutions Class 10 Chapter 1 Real Numbers MCQS are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.