RS Aggarwal Class 10 Solutions Chapter 1 Real Numbers Test Yourself
These Solutions are part of RS Aggarwal Solutions Class 10. Here we have given RS Aggarwal Solutions Class 10 Chapter 1 Real Numbers Test Yourself.
Other Exercises
- RS Aggarwal Solutions Class 10 Chapter 1 Real Numbers Ex 1A
- RS Aggarwal Solutions Class 10 Chapter 1 Real Numbers Ex 1B
- RS Aggarwal Solutions Class 10 Chapter 1 Real Numbers Ex 1C
- RS Aggarwal Solutions Class 10 Chapter 1 Real Numbers Ex 1D
- RS Aggarwal Solutions Class 10 Chapter 1 Real Numbers Ex 1E
- RS Aggarwal Solutions Class 10 Chapter 1 Real Numbers MCQs
- RS Aggarwal Solutions Class 10 Chapter 1 Real Numbers Test Yourself
Question 1.
Solution:
(b)
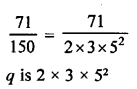
Its decimal will be nonterminating repeating decimal.
Question 2.
Solution:
(b) \(\frac { p }{ q }\) is terminating decimal if q = 2m x 5n
Now, 91 = 7 x 13, 45 = 32 x 5
80 = 24 x 5, 42 = 2 x 3 x 7
80 is of the form 2m x 5n
\(\frac { 19 }{ 80 }\) is terminating decimal expansion,
Question 3.
Solution:
(b) Divisor = 9 and remainder = 7
Let b be the divisor, then
n = 9b + 7
Multiplying both sides by 3 and subtracting 1.
3n – 1 = 3(9b + 7) – 1
3n – 1 = 27b + 21 – 1
3n – 1 = 9(3b) + 9 x 2 + 2
3n – 1 = 9(3b + 2) + 2
Remainder = 2
Question 4.
Solution:
(b) \(0.\bar { 68 }\) + \(0.\bar { 73 }\)
0.686868 ……… + 0.737373……
= 1.424241 = \(1.\bar { 42 }\)
Short-Answer Questions (2 marks)
Question 5.
Solution:
4n, n ∈ N
41 = 4
42 = 4 x 4 = 16
43 = 4 x 4 x 4 = 64
44 = 4 x 4 x 4 x 4 = 256
45 = 4 x 4 x 4 x 4 x 4 = 1024
We see that value of 4n, ends with 4 or 6 only.
Hence, the value of 4n, n ∈ N, never ends with 0.
Question 6.
Solution:
HCF of two numbers = 27 and LCM =162
One number = 81
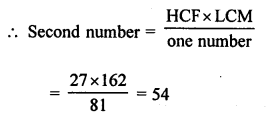
Question 7.
Solution:
\(\frac { 17 }{ 30 }\) = \(\frac { 17 }{ 2 x 3 x 5 }\)
Here, q is in the form of 2m x 5n
It is not terminating decimal.
Question 8.
Solution:

Question 9.
Solution:

Question 10.
Solution:
Let (2 + √3) is rational and 2 is rational.
Difference of them is also rational.
=> (2 + √3) – 2 = 2 + √3 – 2
= √3 is rational
But it contradicts the fact.
(2 + √3) is irrational.
Short-Answer Questions (3 marks)
Question 11.
Solution:
HCF of 12, 15, 18, 27
12 = 2 x 2 x 3 = 22 x 3
15 = 3 x 5
18 = 2 x 3 x 3 = 2 x 32
27 = 3 x 3 x 3 = 33
Now, HCF = 3
and LCM = 22 x 33 x 5 =2 x 2 x 3 x 3 x 3 x 5
= 4 x 27 x 5 = 540
Question 12.
Solution:
Let 2 + √3 and 2 – √3 are two irrational number.
Sum = 2 + √3 + 2 – √3 = 4 which is a rational.
Question 13.
Solution:
4620

Question 14.
Solution:
1008
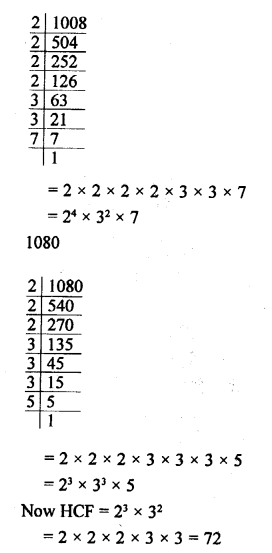
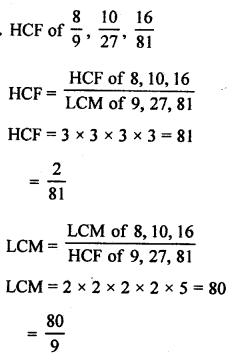
Question 15.
Solution:
Question 16.
Solution:
Give numbers are 546 and 764 and remainders are 6 and 8 respectively.
Remaining number 546 – 6 = 540
and 764 – 8 = 756
Now, required largest number = HCF of 540 and 756 = 108

Long-Answer Questions (4 marks)
Question 17.
Solution:
Let √3 is a rational number.
Let √3 = \(\frac { p }{ q }\) where p and q are integers and have no common factor, other than 1 and q ≠ 0
Squaring both sides.
3 = \(\frac { { p }^{ 2 } }{ { q }^{ 2 } }\) => 3q2 – p2
=> 3 divides p2
=> 3 divides p
Let p = 3c for some integer c
3q2 = 9c2 => q2 – 3c2
=> 3 divides q2 (3 divides 3c2)
=> 3 divides q
3 is common factors of p and q
But it contradicts the fact that p and q have
no common factors and also contradicts that √3 is a rational number.
Hence, √3 is irrational number.
Question 18.
Solution:
Let n be an arbitrary odd positive integer on dividing n by 4, let m be the quotient and r be the remainder.
By Euclid’s division lemma,
n = 4q + r where 0 ≤ r < 4
n = 4q or (4q + 1) or (4q + 2) or (4q + 3)
Clearly, 4q and (4q + 2) are even number
since n is odd.
n ≠ 4q and n ≠ (4q + 2)
n = (4 q + 1) or (4q + 3) for same integer n
Hence, any positive odd integer of the form 4q + 1 or 4q + 3 for some integer q.
Question 19.
Solution:
On dividing n by 3, let q be the quotient and r be the remainder, then
n = 3q + r where 0 ≤ r < 3 => n = 3q + r where r = 0, 1 or 2
n = 3q or n = 3q + 1 or n = 3q + 2
(i) Case (I)
If n = 3q then n is divisible by 3
(ii) Case (II)
If n = (3q + 1) then n + 2 = 3q + 3 = 3q (q + 1) which is divisible by 3
In this case, n + 2 is divisible by 3
(iii) Case (III)
If n = (3q + 2) then n + 1 (n + 1) = 3q + 3 = 3(q + 1) which also divisible by 3
In this case, (n + 1) is divisible by 3
Hence, one and only one out of n, (n + 1) and (n + 2) is divisible by 3.
Question 20.
Solution:
Let (4 + 3√2) is rational number and 4 is also a rational number.
Difference of two rational numbers is also a rational number.
4 + 3√2 – 4 = 3√2 is a rational number
Product of two rational numbers is rational
3 is rational and √2 is rational
But it contradicts the fact
√2 is irrational
Hence, (4 + 3√2 ) is irrational.
Hope given RS Aggarwal Solutions Class 10 Chapter 1 Real Numbers Test Yourself are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.