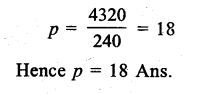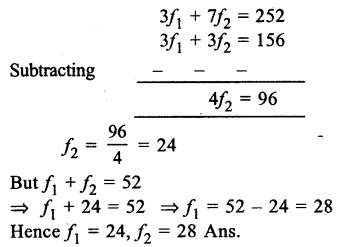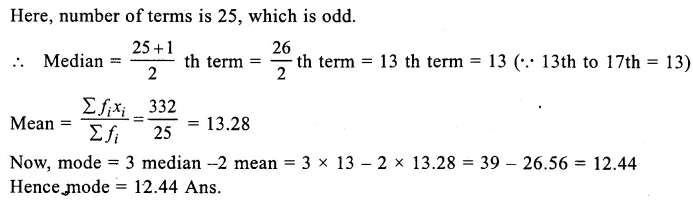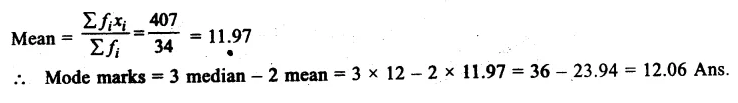RS Aggarwal Class 9 Solutions Chapter 15 Probability Ex 15A
These Solutions are part of RS Aggarwal Solutions Class 9. Here we have given RS Aggarwal Class 9 Solutions Chapter 15 Probability Ex 15A.
Question 1.
Solution:
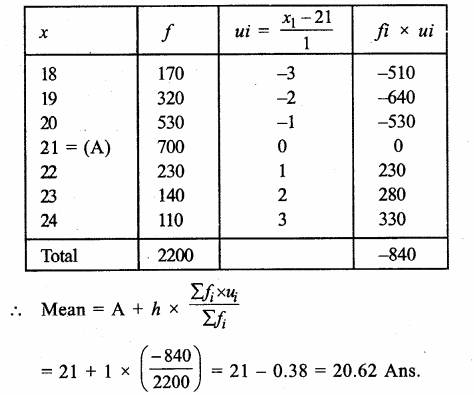
Number of trials = 500 times
Let E be the no. of events in each case, then
∴No. of heads (E1) = 285 times
and no. of tails (E2) = 215 times
∴ Probability in each case will be
∴(i)P(E1) = \(\frac { 285 }{ 500 } \) = \(\frac { 57 }{ 100 } \) = 0.57
(ii) P(E2) = \(\frac { 215 }{ 500 } \) = \(\frac { 43 }{ 100 } \) = 0.43
Question 2.
Solution:
No. of trials = 400
Let E be the no. of events in each case, then
No. of 2 heads (E1) = 112
No. of one head (E2) = 160 times
and no. of O. head (E3) = 128 times
∴ Probability in each case will be:
∴ (i)P(E1) = \(\frac { 112 }{ 400 } \) = \(\frac { 28 }{ 100 } \) = 0.28
(ii)P(E2) = \(\frac { 160 }{ 400 } \) = \(\frac { 40 }{ 100 } \)= 0.40
(iii) P(E3) = \(\frac { 128 }{ 400 } \) = \(\frac { 32 }{ 100 } \) = 0.32 Ans.
Question 3.
Solution:
Number of total trials = 200
Let E be the no. of events in each case, then
No. of three heads (E1) = 39 times
No. of two heads (E2) = 58 times
No. of one head (E3) = 67 times
and no. of no head (E4) = 36 times
∴ Probability in each case will be .
(i) P(E1) = \(\frac { 39 }{ 200 } \) = 0.195
(ii) P(E3) = \(\frac { 67 }{ 200 } \) = 0.335
(iii) P(E4) = \(\frac { 36 }{ 200 } \) = \(\frac { 18 }{ 100 } \) = 0.18
(iv) P(E2) = \(\frac { 58 }{ 200 } \) = \(\frac { 29 }{ 100 } \) = 0.29
Question 4.
Solution:
Solution No. of trials = 300 times
Let E be the no. of events in each case, then
No. of outcome of 1(E1) = 60
No. of outcome of 2(E2) = 72
No. of outcome of 3(E3) = 54
No. of outcome of 4(E4) 42
No. of outcome of 5(E5) = 39
No. of outcome of 6(E6) = 33
The probability of
(i) P(E3) = \(\frac { 54 }{ 300 } \) = \(\frac { 18 }{ 100 } \) = 0.18
(ii) P(E6) = \(\frac { 33 }{ 100 } \) = \(\frac { 11 }{ 100 } \)= 0.11
(iii) P(E5) = \(\frac { 39 }{ 300 } \) = \(\frac { 13 }{ 100 } \) = 0.13
(iv) P(E1) = \(\frac { 60 }{ 300 } \) = \(\frac { 20 }{ 100 } \)= 0.20 Ans.
Question 5.
Solution:
No. of ladies on whom survey was made = 200.
Let E be the no. of events in each case.
No. of ladies who like coffee (E1) = 142
No. of ladies who like coffee (E2) = 58
Probability of
(1) P(E1) = \(\frac { 142 }{ 200 } \) = \(\frac { 71 }{ 100 } \) = 0.71
(ii) P(E2) = \(\frac { 58 }{ 200 } \) = \(\frac { 29 }{ 100 } \) = 0.29 Ans.
Question 6.
Solution:
Total number of tests = 6
No. of test in which the students get more than 60% mark = 2
Probability will he
P(E) = \(\frac { 2 }{ 6 } \) = \(\frac { 1 }{ 3 } \)Ans.
Question 7.
Solution:
No. of vehicles of various types = 240
No. of vehicles of two wheelers = 64.
Probability will be P(E) = \(\frac { 84 }{ 240 } \) = \(\frac { 7 }{ 20 } \) = 0.35 Ans.
Question 8.
Solution:
No. of phone numbers are one page = 200
Let E be the number of events in each case,
Then (i) P(E5) = \(\frac { 24 }{ 200 } \) = \(\frac { 12 }{ 100 } \) = 0.12
(ii) P(E8) = \(\frac { 16 }{ 200 } \) = \(\frac { 8 }{ 100 } \) = 0.08 Ans.
Question 9.
Solution:
No. of students whose blood group is checked = 40
Let E be the no. of events in each case,
Then (i) P(E0) = \(\frac { 14 }{ 40 } \) = \(\frac { 7 }{ 20 } \) = 0.35
(ii) P(EAB) = \(\frac { 6 }{ 40 } \) = \(\frac { 3 }{ 20 } \) = 0.15 Ans.
Question 10.
Solution:
No. of total students = 30.
Let E be the number of elements, this probability will be of interval 21 – 30
P(E) = \(\frac { 6 }{ 30 } \) = \(\frac { 1 }{ 5 } \) = 0.2 Ans.
Question 11.
Solution:
Total number of patients of various age group getting medical treatment = 360
Let E be the number of events, then
(i) No. of patient which are 30 years or more but less than 40 years = 60.
P(E) = \(\frac { 60 }{ 360 } \) = \(\frac { 1 }{ 6 } \)
(ii) 50 years or more but less than 70 years = 50 + 30 = 80
P(E) = \(\frac { 80 }{ 360 } \) = \(\frac { 2 }{ 9 } \)
(iii) Less than 10 years = zero
P(E) = \(\frac { 0 }{ 360 } \) = 0
(iv) 10 years or more 90 + 50 + 60 + 80 + 50 + 30 = 360
Hope given RS Aggarwal Class 9 Solutions Chapter 15 Probability Ex 15A are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.