RS Aggarwal Class 10 Solutions Chapter 1 Real Numbers Ex 1E
These Solutions are part of RS Aggarwal Solutions Class 10. Here we have given RS Aggarwal Solutions Class 10 Chapter 1 Real Numbers Ex 1E.
Other Exercises
- RS Aggarwal Solutions Class 10 Chapter 1 Real Numbers Ex 1A
- RS Aggarwal Solutions Class 10 Chapter 1 Real Numbers Ex 1B
- RS Aggarwal Solutions Class 10 Chapter 1 Real Numbers Ex 1C
- RS Aggarwal Solutions Class 10 Chapter 1 Real Numbers Ex 1D
- RS Aggarwal Solutions Class 10 Chapter 1 Real Numbers Ex 1E
- RS Aggarwal Solutions Class 10 Chapter 1 Real Numbers MCQs
- RS Aggarwal Solutions Class 10 Chapter 1 Real Numbers Test Yourself
Very-Short Answer Questions
Question 1.
Solution:
For any two given positive integers a and b there exist unique whole numbers q and r such that
a = bq + r, where 0 ≤ r < b.
Here, we call ‘a’ as dividend, b as divisor, q is quotient and r as remainder.
Dividend = (Divisor x Quotient) + Remainder
Question 2.
Solution:
Every composite number can be uniquely expressed as a product of two primes, except for the order in which these prime factors occurs.
Question 3.
Solution:
360 = 2 x 2 x 2 x 3 x 3 x 5 = 23 x 3² x 5
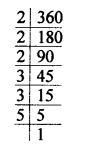
Question 4.
Solution:
We know that HCF of two primes is
HCF (a, b) = 1
Question 5.
Solution:
a and b are two prime numbers then their
LCM = Product of these two numbers
LCM(a, b) = a x b = ab.
Question 6.
Solution:
We know that product of two numbers is equal to their HCF x LCM
LCM = \(\frac { Product of two numbers }{ HCF }\)
= \(\frac { 1050 }{ 25 }\) = 42
LCM of two numbers = 42
Question 7.
Solution:
A composite number is a number which is not a prime. In other words, a composite number has more than two factors.
Question 8.
Solution:
a and b are two primes, then their
HCF will be 1
HCF of a and b = 1
Question 9.
Solution:
\(\frac { a }{ b }\) is a rational number and it has terminating decimal
b will in the form 2m x 5n where m and n are some non-negative integers.
Question 10.
Solution:
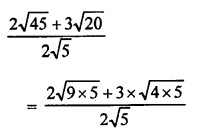
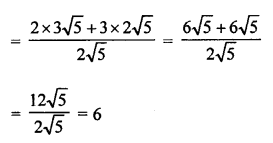
Question 11.
Solution:
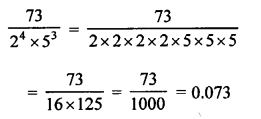
Question 12.
Solution:
2n x 5n = (2 x 5)n = (10)n
Which always ends in a zero
There is no value of n for which (2n x 5n) ends in 5
Question 13.
Solution:
We know that HCF is always a factor is its LCM
But 25 is not a factor of 520
It is not possible to have two numbers having HCF = 25 and LCM = 520
Question 14.
Solution:
Let two irrational number be (5 + √3) and (5 – √3).
Now their sum = (5 + √3) + (5 – √3) = 5 + √3 + 5 – √3 = 10
Which is a rational number.
Question 15.
Solution:
Let the two irrational number be (3 + √2) and (3 – √2)
Now, their product = (3 + √2) (3 – √2)
= (3)² – (√2)² {(a + b) (a – b) = a² – b²}
= 9 – 2 = 7
Which is a rational number.
Question 16.
Solution:
a and b are relative primes
their HCF = 1
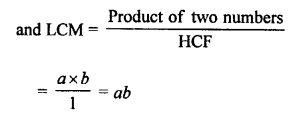
Question 17.
Solution:
LCM of two numbers = 1200
and HCF = 500
But we know that HCF of two numbers divides their LCM.
But 500 does not divide 1200 exactly
Hence, 500 is not their HCF whose LCM is 1200.
Short-Answer Questions
Question 18.
Solution:
Let x = 0.4 = 0.444
Then 10x = 4.444….
Subtracting, we get
9x = 4 => x = \(\frac { 4 }{ 9 }\)
\(\bar { 0.4 }\) = \(\frac { 1 }{ 2 }\) which is in the simplest form.
Question 19.
Solution:
\(\bar { 0.23 }\)
Let x = \(\bar { 0.23 }\) = 0.232323…….
and 100x = 23.232323……
Subtracting, we get
99x = 23 => x = \(\frac { 23 }{ 99 }\)
\(\bar { 0.23 }\) = \(\frac { 23 }{ 99 }\) which is in the simplest form.
Question 20.
Solution:
0.15015001500015
It is non-terminating non-repeating decimal.
It is an irrational number.
Question 21.
Solution:
\(\frac { \surd 2 }{ 3 }\) = \(\frac { 1 }{ 3 }\) √2
Let \(\frac { 1 }{ 3 }\) √2 is a rational number
Product of two rational numbers is a rational
\(\frac { 1 }{ 3 }\) is rational and √2 is rational contradicts
But it contradicts the fact
\(\frac { \surd 2 }{ 3 }\) or \(\frac { 1 }{ 3 }\) √2 is irrational.
Question 22.
Solution:
√3 and 2.
√3 = 1.732 and 2.000
A rational number between 1.732 and 2.000 can be 1.8 or 1.9
Hence, 1.8 or 1.9 is a required rational.
Question 23.
Solution:
\(\bar { 3.1416 }\)
It is non-terminating repeating decimal.
It is a rational number.
Hope given RS Aggarwal Solutions Class 10 Chapter 1 Real Numbers Ex 1E are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.