MCQ Questions

Integrals Class 12 MCQs Questions with Answers

Integration MCQ Class 12 Maths Chapter 7 Question 1.
\(\int \frac{\cos 2 x-\cos 2 \theta}{\cos x-\cos \theta}\) dx is equal to
(A) 2.(sin x + x cos θ) + C
(B) 2(sin x – x cos θ) + C
(C) 2(sin x + 2x cos θ) + C
(D) 2(sin x – 2x cos θ) + C
Answer:
(A) 2.(sin x + x cos θ) + C

Explanation:
I = \(\int \frac{\cos 2 x-\cos 2 \theta}{\cos x-\cos \theta} d x\)
= \(\int \frac{\left(2 \cos ^{2} x-1-2 \cos ^{2} \theta+1\right)}{\cos x-\cos \theta} d x\)
= \(2 \int \frac{(\cos x+\cos \theta)(\cos x-\cos \theta)}{(\cos x-\cos \theta)} d x\)
= 2\(\int(\cos x+\cos \theta) d x\)
= 2 sin x + 2 cos θ + C

MCQ On Integration Class 12 Chapter 7 Question 2.
The value of \(\int_{-\pi / 2}^{\pi / 2}\left(x^{3}+x \cos x+\tan ^{5} x+1\right) d x\) is
(A) O
(B) 2
(C) π
(D) 1
Answer:
(C) π

Explanation:
Let,
= \(\int_{-\pi / 2}^{\pi / 2}\left(x^{3}+x \cos x+\tan ^{5} x+1\right) d x\)
= \(\int_{-\pi / 2}^{\pi / 2} x^{3} d x+\int_{-x / 2}^{\pi / 2} x \cos x+\int_{-\pi / 2}^{\pi / 2} \tan ^{5} x d x+\) + \(\int_{-\pi / 2}^{\pi / 2} 1 \cdot d x\)
it is know that if f(x) is an even function, then \(\int_{-\Omega}^{a} f(x) d x=2 \int_{0}^{a} f(x) d x\)
and if f(x)is an odd function, then
= \(\int_{-a}^{a} f(x) d x=0\)
∴ I = 0 + 0 + 0 + 2\(\int_{0}^{\pi / 2} 1 \cdot d x\)
= \(2[x]_{0}^{\pi / 2}=\frac{2 \pi}{2}=\pi\)
= 2 sin x + 2x cos θ + C

Integration MCQ Questions Class 12 Chapter 7 Question 3.
\(\int \frac{d x}{e^{x}+e^{-x}}\) is equal to ‘
(A) tan^-1 (e^x) + C
(B) tan^-1(e-^x) + C
(C) log(e^x – e^-x) + C
(D) log (e^x + e^-x) + C
Answer:
(A) tan^-1 (e^x) + C

Explanation:
Let
I = \(2[x]_{0}^{\pi / 2}=\frac{2 \pi}{2}=\pi\)
= \(2[x]_{0}^{\pi / 2}=\frac{2 \pi}{2}=\pi\)
Also, let e^x = t
e^x dx = dt
I = \(\int \frac{d t}{1+t^{2}}\)
= tan^-1 t + C
= tan^-1 (e^x) + C

MCQ On Integration Class 12 Question 4.
\(\int \frac{\cos 2 x}{(\sin x+\cos x)^{2}}\) is equal to
(A) \(\frac{-1}{\sin x+\cos x}+C\)
(B) \(\log |\sin x+\cos x|+C\)
(C) \(\log |\sin x-\cos x|+C\)
(D) \(\frac{1}{(\sin x+\cos x)^{2}}\)
Answer:
(B) \(\log |\sin x+\cos x|+C\)

Explanation:
Let
I = \(\frac{\cos 2 x}{(\cos x+\sin x)^{2}}\)
I = \(\int \frac{\cos ^{2} x-\sin ^{2} x}{(\cos x+\sin x)^{2}} d x\)
= \(\int \frac{(\cos x+\sin x)(\cos x-\sin x)}{(\cos x+\sin x)^{2}} d x\)
= \(\int \frac{\cos x-\sin x}{\cos x+\sin x} d x\)
Let cos x + sin x = t
⇒ (cos x – sin x) dx = dt
⇒ I = \(\int \frac{d t}{t}\)
= log |t| + C
= log |cos x = sin x |+ C

Integration MCQs Class 12 Chapter 7 Question 5.
if f(a + b – x) = f(x), then \(\int_{a}^{b} x f(x) d x\) is equal to
(A) \(\frac{a+b}{2} \int_{a}^{b} f(b-x) d x\)
(B) \(\frac{a+b}{2} \int_{a}^{b} f(b+x) d x\)
(C) \(\frac{b-a}{2} \int_{a}^{b} f(x) d x\)
(D) \(\frac{a+b}{2} \int_{a}^{b} f(x) d x\)
Answer:.
(D) \(\frac{a+b}{2} \int_{a}^{b} f(x) d x\)

Explanation:
Let
I = \(\int_{a}^{b} x f(x) d x\)
I = \(\int_{a}^{b}(a+b-x) f(a+b-x) d x\) [∵\(\int_{a}^{b} f(x) d x=\int_{a}^{b} f(a+b-x) d x\)]
⇒ I = \(\int_{a}^{b}(a+b-x) f(x) d x\)
⇒I = \((a+b) \int_{a}^{b} f(x) d x-I\) – I [Using Equestion(i)]
⇒ I + I = \((a+b) \int_{a}^{b} f(x) d x\)
⇒ 2I = \((a+b) \int_{a}^{b} f(x) d x\)
⇒ I = \(\left(\frac{a+b}{2}\right) \int_{a}^{b} f(x) d x\)

MCQ Of Integration Class 12 Chapter 7 Question 6.
The Value of \(\int_{0}^{1} \tan ^{-1}\left(\frac{2 x-1}{1+x-x^{2}}\right) d x\) is
(A) 1
(B) 0
(C) -1
(D) \(\frac {π}{4}\)
Answer:
(B) 0

Explanation:
Let
⇒ I = \(\int_{0}^{1} \tan ^{-1}\left(\frac{2 x-1}{1+x-x^{2}}\right) d x\)
⇒ I = \(\int_{0}^{1} \tan ^{-1}\left(\frac{x-(1-x)}{1+x(1-x)}\right) d x\)
⇒ I = \(\int_{0}^{1}\left[\tan ^{-1} x-\tan ^{-1}(1-x)\right] d x\) ……….(i)
⇒ I = \(\int_{0}^{1}\left[\tan ^{-1}(1-x)-\tan ^{-1}(1-1+x)\right] d x\)
⇒ I = \(\int_{0}^{1}\left[\tan ^{-1}(1-x)-\tan ^{-1}(x)\right] d x\)
⇒ I = \(\int_{0}^{1}\left[\tan ^{-1}(1-x)-\tan ^{-1}(x)\right] d x\) ………(ii)
Adding equestion(i) and (ii), we obtained
2I = \(\int_{0}^{1}\left(\tan ^{-1} x+\tan ^{-1}(1-x)\right.\) – \(\left.-\tan ^{-1}(1-x)-\tan ^{-1} x\right) d x\)
⇒ I = 0

MCQs On Integration Class 12 Chapter 7 Question 7.
\(\int_{0}^{1} \tan ^{-1}\left(\frac{2 x-1}{1+x-x^{2}}\right) d x\) is equal to
(A) \(\sin (b-a) \log \left|\frac{\sin (x – b)}{\sin (x – a)}\right|+C\)

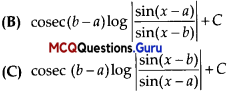
(D) \(\sin (b-a) \log \left|\frac{\sin (x – a)}{\sin (x – b)}\right|+C\)
Answer:.
Option (C) is correct.

Explanation:
Let
I = \(\int \frac{d x}{\sin (x-a) \sin (x-b)}\)
= \(\frac{1}{\sin (b-a)} \int \frac{\sin (b-a)}{\sin (x-a) \sin (x-b)} d x\)
= \(\frac{1}{\sin (b-a)} \int \frac{\sin (x-a-x+b)}{\sin (x-a) \sin (x-b)} d x\)
= \(\frac{1}{\sin (b-a)} \int \frac{\sin \{(x-a)-(x-b)\}}{\sin (x-a) \sin (x-b)} d x\)
sin (x – a) cos (x – b) –
= \(\frac{1}{\sin (b-a)} \int \frac{\cos (x-a) \sin (x-b)}{\sin (x-a) \sin (x-b)} d x\)
= \(\frac{1}{\sin (b-a)} \int[\cot (x-b)-\cot (x-a)] d x\)
= \(\frac{1}{\sin (b-a)}[\log |\sin (x-b)|-\log |\sin (x-a)|]+C\)

Integration MCQ With Answers Pdf Class 12 Chapter 7 Question 8.
\(\int \sqrt{1+x^{2}} d x\) is equal to
(A) \(\frac{x}{2} \sqrt{1+x^{2}}+\frac{1}{2} \log \left|\left(x+\sqrt{1+x^{2}}\right)\right|+C\)
(B) \(\frac{2}{3}\left(1+x^{2}\right)^{3 / 2}+C\)
(C) \(\frac{2}{3} x\left(1+x^{2}\right)^{3 / 2}+C\)
(D) \(\frac{x^{2}}{2} \sqrt{1+x^{2}}+\frac{1}{2} x^{2} \log \left(x+\sqrt{1+x^{2}}\right)+C\)
Answer:
(A) \(\frac{x}{2} \sqrt{1+x^{2}}+\frac{1}{2} \log \left|\left(x+\sqrt{1+x^{2}}\right)\right|+C\)

Explanation:
it is known that,
\(\int \sqrt{a^{2}+x^{2}} d x=\frac{x}{2} \sqrt{a^{2}+x^{2}}\) + \(+\frac{a^{2}}{2} \log \left|x+\sqrt{x^{2}+a^{2}}\right|+C\)
\(\int \sqrt{1+x^{2}} d x=\frac{x}{2} \sqrt{1+x^{2}}\) + \(+\frac{1}{2} \log \left|x+\sqrt{1+x^{2}}\right|+C\)

MCQ Integration Class 12 Chapter 7 Question 9.
\(\int \frac{x d x}{(x-1)(x-2)}\) is equal to
(A) \(\log \left|\frac{(x-1)^{2}}{x-2}\right|+C\)
(B) \(\log \left|\frac{(x-2)^{2}}{x-1}\right|+C\)
(C) \(\log \left|\frac{(x-2)^{2}}{x-1}\right|+C\)
(D) \(\log |(x-1)(x-2)|+C\)
Answer:
(B) \(\log \left|\frac{(x-2)^{2}}{x-1}\right|+C\)

Explanation:
Let
\(\frac{x}{(x-1)(x-2)}=\frac{A}{(x-1)}+\frac{B}{(x-2)}\)
x = A(x – 2) + B (x – 1) ………..(i)
Substituting x = 1 and 2 in Equestion (i), we obtained
A = -1 and B = 2
∴ \(\frac{x}{(x-1)(x-2)}=-\frac{1}{(x-1)}+\frac{2}{(x-2)}\)
\(\int \frac{x}{(x-1)(x-2)} d x=\int\left\{\frac{-1}{(x-1)}+\frac{2}{(x-2)}\right\} d x\)
= -log |x – 1| + 2 log |x – 2| + C
\(\log \left|\frac{(x-2)^{2}}{x-1}\right|+C\)

Integral MCQ Questions Class 12 Chapter 7 Question 10.
If f(x) = \(\int_{0}^{x} t \sin t d t\), then f'(x) is
(A) cos x + x sin x
(B) x sin x
(C) x cos x
(D) sin x + x cos x
Answer:
(B) x sin x

Explanation:
f(x) = \(\int_{0}^{x} t \sin t d t\)
Integrating by parts, we obtain
f(x) = \(t \int_{0}^{x} \sin t d t-\int_{0}^{x}\left\{\left(\frac{d}{d t} t\right) \int \sin t d t\right\} d t\)
= \([t(-\cos t)]_{0}^{x}-\int_{0}^{x}(-\cos t) d t\)
= [-t cost + sin t]x0
= -x cos x + sin x
= f'(x) = -[{x(- sin x)}+cos x] + cos x
x sin x – cos x + cos x
= x sin x

Integration MCQ Class 12 Chapter 7 Question 11.
\(\int \tan ^{-1} \sqrt{x} d x\) is equal to
(A) (x + 1)tan^-1\(\sqrt{x}-\sqrt{x}\) + C
(B) x tan^-1\(\sqrt{x}-\sqrt{x}\) + C
(C) \(\sqrt{x}-\sqrt{x}\) tan-1\(\sqrt{x}\) + C
(D) \(\sqrt{x}\) – (x + )tan \(\sqrt{x}\) + C
Answer:
(A) (x + 1)tan^-1\(\sqrt{x}-\sqrt{x}\) + C

Explanation:
Let,
I = \(\int 1 \cdot \tan ^{-1} \sqrt{x} d x\)
= tan^-1 \(\sqrt{x} \cdot x-\frac{1}{2} \int \frac{1}{(1+x)} \cdot \frac{2}{\sqrt{x}} d x\)
=x tan^-1 \(\sqrt{x}-\frac{1}{2} \int \frac{2}{\sqrt{x}(1+x)} d x\)
Put x = t²
⇒ dx = 2t dt
∴ I = x tan^-1\(\sqrt{x}\) – \(\int \frac{t}{t\left(1+t^{2}\right)} d t\)
x = tan^-1\(\sqrt{x}\) – \(\int \frac{t^{2}}{1+t^{2}} d t\)
= tan^-1\(\sqrt{x}\) – \(\int\left(1-\frac{1}{1+t^{2}}\right) d t\)
= tan^-1\(\sqrt{x}\) – \(\int\left(1-\frac{1}{1+t^{2}}\right) d t\)
= \(x \tan ^{-1} \sqrt{x}-\sqrt{x}+\tan ^{-1} t+C\)
= \(x \tan ^{-1} \sqrt{x}-\sqrt{x}+\tan ^{-1} \sqrt{x}+C\)
= \((x+1) \tan ^{-1} \sqrt{x}-\sqrt{x}+C\)

Integral MCQ Class 12 Chapter 7 Question 12.
\(\int x^{2} e^{x^{3}} d x\) is equal to
(A) \(\frac{1}{3} e^{x^{3}}+C\)
(B) \(\frac{1}{3} e^{x^{2}}+C\)
(C) \(\frac{1}{2} e^{x^{3}}+C\)
(D) \(\frac{1}{2} e^{x^{2}}+C\)
Answer:
(A) \(\frac{1}{3} e^{x^{3}}+C\)

Explanation:
Let,
I = \(\int x^{2} e^{x^{3}} d x\)
Also, let x³ = t
⇒ 3 x² dx = dt
⇒ I = \(\frac{1}{3} \int e^{t} d t\)
= \(\frac{1}{3}\)(et) + C
= \(\frac{1}{3} e^{x^{3}}+C\)

Integration MCQs Class 12 Chapter 7 Question 13.
\(\int e^{x} \sec x(1+\tan x) d x\) is equal to
(A) e^x cos x + C
(B) e^x sec x + C
(C) e^x sin x + C
(D) e^x tan x + C
Answer:
(B) e^x sec x + C

Explanation:
\(\int e^{x} \sec x(1+\tan x) d x\)
Let
I = \(\int e^{x} \sec x(1+\tan x) d x=\int e^{x}(\sec x+\sec x \tan x) d x\)
Also, let sec x = f(x) ⇒sec x tan x = f'(x)
It is known that, \(\int e^{x}\left\{f(x)+f^{\prime}(x)\right\} d x=e^{x} f(x)+C\)
∴ e^x sec x + C

Integration Class 12 MCQ Chapter 7 Question 14.
\(\int \frac{\sin ^{2} x-\cos ^{2} x}{\sin ^{2} x \cos ^{2} x}\) dx is equal to
(A) tan x + cot x + C
(B) tan x + cosec x + C
(C) -tan x + cot x + C
(D) tan x + sec x + C
Answer:
(A) tan x + Cot x + C

Explanation:
\(\int \frac{\sin ^{2} x-\cos ^{2} x}{\sin ^{2} x \cos ^{2} x} d x=\int\left(\frac{\sin ^{2} x}{\sin ^{2} x \cos ^{2} x}-\frac{\cos ^{2} x}{\sin ^{2} x \cos ^{2} x}\right) d x\)
=
= tan x + cot x+ C

MCQ Of Integration Chapter 7 Class 12 Question 15.
\(\int \frac{d x}{\sin ^{2} x \cos ^{2} x}\) equal to
(A) tan x + cot x + C
(B) tan x – cot x + C
(C) tan x cot x + C
(D) tan x – cot 2x + C
Answer:
(B) tan x – cot x + C

Explanation:
Let
I = \(\int \frac{d x}{\sin ^{2} x \cos ^{2} x}\)
= \(\int \frac{1}{\sin ^{2} x \cos ^{2} x} d x\)
= \(\int \frac{\sin ^{2} x+\cos ^{2} x}{\sin ^{2} x \cos ^{2} x} d x\)
= \(\int \frac{\sin ^{2} x}{\sin ^{2} x \cos ^{2} x} d x+\int \frac{\cos ^{2} x}{\sin ^{2} x \cos ^{2} x} d x\)
=
= tan x – cot x + C

Question 16.
\(\int \frac{x^{9}}{\left(4 x^{2}+1\right)^{6}} d x\) is equal to
(A) \(\frac{1}{5 x}\left(4+\frac{1}{x^{2}}\right)^{-5}+C\)
(B) \(\frac{1}{5}\left(4+\frac{1}{x^{2}}\right)^{-5}+C\)
(C) \(\frac{1}{10 x}(1+4)^{-5}+C\)
(D) \(\frac{1}{10}\left(\frac{1}{x^{2}}+4\right)^{-5}+C\)
Answer:
(D) \(\frac{1}{10}\left(\frac{1}{x^{2}}+4\right)^{-5}+C\)

Explanation:
I = \(\int \frac{x^{9}}{\left(4 x^{2}+1\right)^{6}} d x\)
= \(\int \frac{x^{9}}{x^{12}\left(4+\frac{1}{x^{2}}\right)^{6}} d x\)
= \(\int \frac{d x}{x^{3}\left(4+\frac{1}{x^{2}}\right)^{6}}\)

put 4 + \(\frac{1}{x^{2}}\) = t
⇒ \(\frac{-2}{x^{3}}\) dx = dt
⇒ \(\frac{-2}{x^{3}}\) dx = –\(\frac{1}{2}\) dt
∴ I = \(\frac{1}{2} \int \frac{d t}{t^{6}}\)
= \(-\frac{1}{2}\left[\frac{t^{-6+1}}{-6+1}\right]+C\)
= \(\frac{1}{10}\left[\frac{1}{t^{5}}\right]+C\)
= \(\frac{1}{10}\left(4+\frac{1}{x^{2}}\right)^{-5}+C\)

Question 17.
\(\frac{1}{x^{2}}\) is equal to
(A) \(x+\frac{x^{2}}{2}+\frac{x^{3}}{3}-\log |1-x|+C\)
(B) \(x+\frac{x^{2}}{2}-\frac{x^{3}}{3}-\log |1-x|+C\)
(C) \(x-\frac{x^{2}}{2}-\frac{x^{3}}{3}-\log |1+x|+C\)
(D) \(x-\frac{x^{2}}{2}+\frac{x^{3}}{3}-\log |1+x|+C\)
Answer:
(D) \(x-\frac{x^{2}}{2}+\frac{x^{3}}{3}-\log |1+x|+C\)

Explanation:
Let
I = \(\int \frac{x^{3}}{x+1} d x\)
= \(\int\left(\left(x^{2}-x+1\right)-\frac{1}{(x+1)}\right) d x\)
= \(\frac{x^{3}}{3}-\frac{x^{2}}{2}+x-\log |x+1|+C\)

Question 18.
if \(\int \frac{x^{3} d x}{\sqrt{1+x^{2}}}=a\left(1+x^{2}\right)^{3 / 2}+b \sqrt{1+x^{2}}+C\) then
(A) a = \(\frac {1}{3}\), b = 1
(B) a = \(\frac {-1}{3}\), b = 1
(C) a = \(\frac {-1}{3}\), b = -1
(D) a = \(\frac {-1}{3}\), b = -1
Answer:.
(D) a = \(\frac {-1}{3}\), b = -1

Explanation:
Let
I = \(\int \frac{x^{3}}{\sqrt{1+x^{2}}} d x\)
= \(a\left(1+x^{2}\right)^{3 / 2}+b \sqrt{1+x^{2}}+C\)
I = \(\int \frac{x^{3}}{\sqrt{1+x^{2}}} d x\)
= \(\int \frac{x^{2} \cdot x}{\sqrt{1+x^{2}}} d x\)
Put 1 + x² = t²
⇒ 2x dx = 2t dt
∴ I = \(\int \frac{t\left(t^{2}-1\right)}{t} d t\)
= \(\frac{t^{3}}{3}-t+C\)
= \(\frac{1}{3}\left(1+x^{2}\right)^{3 / 2}-\sqrt{1+x^{2}}+C\)
∴ a = \(\frac {-1}{3}\), b = -1

Question 19.
\(\int_{-\pi / 4}^{\pi / 4} \frac{d x}{1+\cos 2 x}\) is equal to
(A) 1
(B) 2
(C) 3
(D) 4
Answer:
(D) 4

Explanation:
Let
I = \(\int_{-\pi / 4}^{\pi / 4} \frac{d x}{1+\cos 2 x}\)
= \(\int_{-\pi / 4}^{\pi / 4} \frac{d x}{2 \cos ^{2} x}\)
= \(\frac{1}{2} \int_{-\pi / 4}^{\pi / 4} \sec ^{2} x d x\)
= \(\int_{0}^{\pi / 4} \sec ^{2} x d x\)
= \([\tan x]_{0}^{\pi / 4}\)
= 1

Question 20.
\(\int \frac{d x}{x^{2}+2 x+2}\) equals
(A) x tan^-1 (x + 1) + C
(B) tan^-1 (x + 1) + C
(C) (x + 1) tan^-1 + C
(D) tan^-1 + C
Answer:
(B) tan^-1 (x + 1) + C

Explanation:
\(\int \frac{d x}{x^{2}+2 x+2}=\int \frac{d x}{\left(x^{2}+2 x+1\right)+1}\)
= \(\int \frac{1}{(x+1)^{2}+(1)^{2}} d x\)
= \(\left[\tan ^{-1}(x+1)\right]+C\)

Question 21.
\(\int \frac{d x}{x^{2}+2 x+2}\) is equal to
(A) \(2 \sqrt{2}\)
(B) \(2(\sqrt{2}+1)\)
(C) 2
(D) \(2(\sqrt{2}-1)\)
Answer:
(D) \(2(\sqrt{2}-1)\)

Explanation:
Let
I = \(\int_{0}^{\pi / 2} \sqrt{1-\sin 2 x} d x\)
= \(\int_{0}^{\pi / 4} \sqrt{(\cos x-\sin x)^{2}} d x\) + \(+\int_{\pi / 4}^{\pi / 2} \sqrt{(\sin x-\cos x)^{2}} d x\)
= \([\sin x+\cos x]_{0}^{\pi / 4}+[-\cos x-\sin x]_{\pi / 4}^{\pi / 2}\)
= \(\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{2}}-0-1+\left(-0-1+\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{2}}\right) \)
= \(2(\sqrt{2}-2)\)
= \(2(\sqrt{2}-1)\)

Question 22.
The anti-derivative of \(\left(\sqrt{x}+\frac{1}{\sqrt{x}}\right)\) equals
(A) \(\frac{1}{3} x^{1 / 3}+2 x^{1 / 2}+C\)
(B) \(\frac{2}{3} x^{2 / 3}+\frac{1}{2} x^{2}+C\)
(C) \(\frac{2}{3} x^{2 / 3}+2 x^{1 / 2}+C\)
(D) \(\frac{3}{2} x^{3 / 2}+\frac{1}{2} x^{1 / 2}+C\)
Answer:
(D) \(\frac{3}{2} x^{3 / 2}+\frac{1}{2} x^{1 / 2}+C\)

Explanation:
\(\left(\sqrt{x}+\frac{1}{\sqrt{x}}\right) d x=\int x^{1 / 2} d x+\int x^{-1 / 2} d x\)
\(=\frac{x^{3 / 2}}{\frac{3}{2}}+\frac{x^{1 / 2}}{\frac{1}{2}}+C\)
= \(\frac{2}{3} x^{3 / 2}+2 x^{1 / 2}+C\)

Question 23.
\(\int_{1}^{\sqrt{3}} \frac{d x}{1+x^{2}}\) equals
(A) \(\frac {π}{3}\)
(B) \(\frac {2π}{3}\)
(C) \(\frac {π}{6}\)
(D) \(\frac {π}{12}\)
Answer:
(D) \(\frac {π}{12}\)

Explanation:
\(\int_{1}^{\sqrt{3}} \frac{d x}{1+x^{2}}=F(\sqrt{3})-F(1)\)
= tan-1\(\sqrt{3}\) – tan^-1 1
= \(\frac {π}{3}\) – \(\frac {π}{4}\)
= \(\frac {π}{12}\)

Question 24.
\(\int_{0}^{2 / 3} \frac{d x}{4+9 x^{2}}\) equals
(A) \(\frac {π}{6}\)
(B) \(\frac {π}{12}\)
(C) \(\frac {π}{24}\)
(D) \(\frac {π}{4}\)
Answer:
(C) \(\frac {π}{24}\)

Explanation:
\(\int \frac{d x}{4+9 x^{2}}=\int \frac{d x}{(2)^{2}+(3 x)^{2}}\)
Put 3x = t
⇒ 3dx = dt
∴ \(\int \frac{d x}{(2)^{2}+(3 x)^{2}}=\frac{1}{3} \int \frac{d t}{(2)^{2}+(t)^{2}}\)
= \(\frac{1}{3}\left[\frac{1}{2} \tan ^{-1} \frac{t}{2}\right]\)
= \(\frac{1}{6} \tan ^{-1}\left(\frac{3 x}{2}\right)\)
= F(x)

By second fundamental theorem of calculus, we obtain
\(\int_{0}^{2 / 3} \frac{d x}{4+9 x^{2}}=F\left(\frac{2}{3}\right)-F(0)\)
= \(\frac{1}{6} \tan ^{-1}\left[\frac{3}{2} \times \frac{2}{3}\right]-\frac{1}{6} \tan ^{-1}(0)\)
= \(\frac{1}{6} \tan ^{-1}(1)\)
= \(\frac{1}{6} \tan ^{-1}\left[\tan \frac{\pi}{4}\right]\)
= \(\frac{\pi}{24}\)

Question 25.
If \(\frac{d}{d x} f(x)=4 x^{3}-\frac{3}{x^{4}}\) such that f(2) = 0. Then f(x) is
(A) \(x^{4}+\frac{1}{x^{3}}-\frac{129}{8}\)
(B) \(x^{3}+\frac{1}{x^{4}}+\frac{129}{8}\)
(C) \(x^{4}+\frac{1}{x^{3}}+\frac{129}{8}\)
(D) \(x^{3}+\frac{1}{x^{4}}-\frac{129}{8}\)
Answer:
(C) \(x^{4}+\frac{1}{x^{3}}+\frac{129}{8}\)

Explanation:
It is given that,
\(\frac {d}{dx}\) f(x) = 4 x 3 – \(\frac{3}{x^{4}}\)
∴ Anti – derivauve of 4×3 – \(\frac{3}{x^{4}}\) = f(x)
∴ f(x) = \(\frac{3}{x^{4}}\)
f(x) = \(\frac{3}{x^{4}}\)
f(x) = \(\frac{3}{x^{4}}\)
f(x) = \(\frac{3}{x^{4}}\)
Also,
f(2) = 0
f(2) = (2)⁴ + \(\frac{1}{2^{3}}\) + C = 0
⇒ \(16+\frac{1}{8}+C\) = 0
⇒ C = –\(16+\frac{1}{8}\)
⇒ C = \(\frac{-129}{8}\)
∴ f(x) = \(x^{4}+\frac{1}{x^{3}}-\frac{129}{8}\)

Assertion And Reason Based MCQs (1 Mark each)

Directions¡In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as:
(A) Both A and R are true and R is the correct explanation of A
(B) Both A and R are true but R is NOT the correct explanation of A
(C) A is true but R is false
(D) A is false and R is True

Question 1.
Assertion (A): \(\int \frac{d x}{x^{2}+2 x+3}=\frac{1}{\sqrt{2}} \tan ^{-1}\left(\frac{x+1}{\sqrt{2}}\right)+c\)
Reason (R): \(\int \frac{d x}{x^{2}+a^{2}}=\frac{1}{a} \tan ^{-1}\left(\frac{x}{a}\right)+c\)
Answer:
(A) Both A and R are true and R is the correct explanation of A

Explanation:
\(\int \frac{d x}{x^{2}+a^{2}}=\frac{1}{a} \tan ^{-1}\left(\frac{x}{a}\right)+c\)
This is a standard integral and hence R is true.
\(\int \frac{d x}{x^{2}+2 x+3}=\int \frac{d x}{(x+1)^{2}+(\sqrt{2})^{2}}\)
= \(\frac{1}{\sqrt{2}} \tan ^{-1}\left(\frac{x+1}{\sqrt{2}}\right)+c\)
Hence A is true and R is the correct explanation for A.

Question 2.
Assertion(A): \(\int e^{x}[\sin x-\cos x] d x=e^{x} \sin x+C\)
Reason (R): \(\int e^{x}\left[f(x)+f^{\prime}(x)\right] d x=e^{x} f(x)+c\)
Answer:
(D) A is false and R is True

Explanation:
\(\int e^{x}\left[f(x)+f^{\prime}(x)\right] d x\) = \(\int e^{x} f(x) d x+\int e^{x} f^{\prime}(x) d x\)
= \(f(x) e^{x}-\int f^{\prime}(x) e^{x} d x\) + \(+\int f^{\prime}(x) e^{x} d x\)
= \(e^{x} f(x)+c\)
Hence R is true.
\(\int e^{x}(\sin x-\cos x) d x\) = \(e^{x}(-\cos x)+c\)
= \(e^{x}(\cos x)+c\) [∵\(\frac{d}{d x}(-\cos x)=\sin x\)]
Hence A is false.

Question 3.
Assertion (A): \(\int x^{x}(1+\log x) d x=x^{x}+c\)
Reason (R): \(\frac{d}{d x}\left(x^{x}\right)=x^{x}(1+\log x)\)
Answer:
(A) Both A and R are true and R is the correct explanation of A

Explanation:
Let y = x³
log y = x log x
Differentiating w,r.t. x
\(\frac{1}{y} \frac{d y}{d x}=x\left(\frac{1}{x}\right)+\log x(1)\)
\(\frac{d y}{d x}=y(1+\log x)\)
= x^x(1+log x)
Hence R is true.
Since \(\frac {d}{dx}\)(x^x) = x^x(1 + log x)
\(\int x^{x}(1+\log x) d x\) = x^x + c
Using the concept of anti-derivative, A is true.
R is the correct explanation for A.

Question 4.
Assertion (A): \(\int x^{2} d x=\frac{x^{3}}{3}+c\)
Reason (R): \(\int e^{x^{2}} d x=e^{x^{3 / 3}}+c\)
Answer:
(C) A is true but R is false

Explanation:
Since
\(\int e^{x^{2}} d x=e^{x^{3 / 3}}+c\)
\(\int e^{x^{2}} d x=e^{x^{3 / 3}}+c\)
= \(\int e^{x^{2}} d x=e^{x^{3 / 3}}+c\)
∴ A is true.
\(\int e^{x^{2}}\) dx is a function
which can not be integrated.
∴ R is false.

Question 5.
Assertion (A): \(\int_{0}^{\pi / 2} \frac{\cos x}{\sin x+\cos x} d x=\frac{\pi}{4}\)
Reason (R): \(\int_{0}^{\pi / 2} \frac{\sin x}{\sin x+\cos x} d x=\frac{\pi}{4}\)
Answer:
(A) Both A and R are true and R is the correct explanation of A

Explanation:
Let I = \(\int_{0}^{\pi / 2} \frac{\sin x}{\sin x+\cos x} d x\) ………(i)
\(\int_{0}^{a} f(x) d x=\int_{0}^{a} f(a-x) d x\)
∴ \(I=\int_{0}^{\pi / 2} \frac{\sin \left(\frac{\pi}{2}-x\right) d x}{\sin \left(\frac{\pi}{2}-x\right)+\cos \left(\frac{\pi}{2}-x\right)}\)
I = \(\int \frac{\cos x}{\cos x+\sin x} d x\) ……….(ii)
Adding equations (i) + (ii),
2I = \(\int_{0}^{\pi / 2} \frac{\sin x+\cos x}{\sin x+\cos x} d x\)
= \(\int_{0}^{\pi / 2} 1 d x\)
= \([x]_{0}^{\pi / 2}\)
= \(\frac {π}{2}\)
I = \(\frac {π}{4}\)
Hence R is true.
From (ii), A is also true.
R is the correct explanation for A.

Question 6.
Assertion (A): \(\int_{-3}^{3}\left(x^{3}+5\right) d x=30\)
Reason (R): f(x) = x³ + 5 is an odd function
Answer:
(C) A is true but R is false

Explanation:
Let f(x) = x³ + 5
f(-x) = (-x)³ + 5
= -x³ + 5
f(x) is neither even nor odd. Hence R is false.
\(\int_{-3}^{3}\left(x^{3}+5\right) d x=30\) = 0 [∴x³ is odd]
\(\int_{-3}^{3} 5 d x=5[x]_{-3}^{3}=30\)
∴ \(\int_{-3}^{3}\left(x^{3}+5\right) d x=0+30=30\)
Hence A is true.

Question 7.
Assertion (A): \(\frac{d}{d x}\left[\int_{0}^{x^{2}} \frac{d t}{t^{2}+4}\right]=\frac{2 x}{x^{4}+4}\)
Reason (R): \(\int \frac{d x}{x^{2}+a^{2}}=\frac{1}{a} \tan ^{-1}\left(\frac{x}{a}\right)+c\)
Answer:
(A) Both A and R are true and R is the correct explanation of A

Explanation:
\(\int \frac{d x}{x^{2}+a^{2}}=\frac{1}{a} \tan ^{-1}\left(\frac{x}{a}\right)+c\)
: This is a standard integral and hence true.
So R is true.
\(\int_{0}^{x^{2}} \frac{d t}{t^{2}+4}=\left[\frac{1}{2} \tan ^{-1}\left(\frac{t}{2}\right)\right]_{0}^{x^{2}}\)
= \(\frac{1}{2} \tan ^{-1}\left(\frac{x^{2}}{2}\right)\)
\(\frac{d}{d x}\left[\int_{0}^{x^{2}} \frac{d t}{t^{2}+4}\right]=\frac{d}{d x}\left[\frac{1}{2} \tan ^{-1}\left(\frac{x^{2}}{2}\right)\right]\)
= \(\frac{1}{2} \times \frac{1}{1+\frac{x^{4}}{4}} \times \frac{2 x}{2}\)
= \(\frac{x}{2} \times \frac{4}{4+x^{4}}\)
= \(\frac{2 x}{4+x^{4}}\)
Hence A is true and R is the correct explanation for A.

Question 8.
Assertion (A): \(\int_{-1}^{1}\left(x^{3}+\sin x+2\right) d x\) = 0
Reason (R):

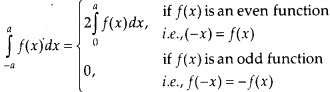
Answer:
(D) A is false and R is True

Explanation:

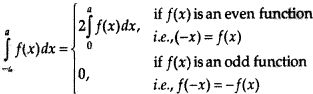
This is a property of the definite integrals and hence R is true.
\(\int_{-1}^{1}\left(x^{3}+\sin x+2\right) d x\) = 0

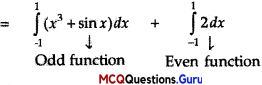
= \(0+2[x]_{-1}^{1}\)
= 2 x 2
= 4
Hence A is false.

Case-Based MCQs

Attempt any four sub-parts from each question.
Each sub-part carries 1 mark.

I. Read the following text and answer the following questions on the basis of the same:

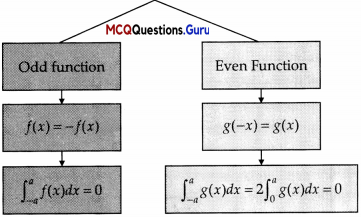
Question 1.
\(\int_{-1}^{1} x^{99}\) dx = …………….
(A) 0
(B) 1
(C) -1
(D) 2
Answer:
(A) 0

Explanation:
\(\int_{-1}^{1} x^{99}\) dx = 0, since x⁹⁹ is an odd function.

Question 2.
\(\int_{-\pi}^{\pi} x \cos x d x\) = …………..
(A) 1
(B) 0
(C) -1
(D) \(\frac {π}{2}\)
Answer:
(B) 0

Explanation:
\(\int_{-\pi}^{\pi} x \cos x d x\) = 0, since x cos x is an odd function.

Question 3.
\(\int_{-\pi / 2}^{\pi / 2} \sin ^{3} x d x\) = …………..
(A) 1
(B) 0
(C) -1
(D) π
Answer:
(B) 0

Explanation:
\(\int_{-\pi / 2}^{\pi / 2} \sin ^{3} x d x\) = 0, since sin³x dx = 0 is an odd function.

Question 4.
\(\int_{-\pi / 2}^{\pi / 2} \sin ^{3} x d x\) = …………..
(A) π
(B) 0
(C) 2π
(D) \(\frac {π}{2}\)
Answer:
(C) 2π

Explanation:
Since x sin x is an even function
\(\int_{-\pi}^{\pi} x \sin x d x\) = \(2 \int_{0}^{\pi} x \sin x d x\)
= 2 \(2\left[-x \cos x+\int(1 \times \cos x d x)\right]_{0}^{\pi}\)
= 2 \(2[-x \cos x+\sin x]_{0}^{\pi}\)
= 2[(π + 0) – (0 + 0)]
= 2π

Question 5.
\(\int_{-\pi}^{\pi} \tan x \sec ^{2} x d x\) = …………..
(A) 1
(B) -1
(C) 0
(D) 2
Answer:
(C) 0

Explanation:
\(\int_{-\pi}^{\pi} \tan x \sec ^{2} x d x\) = 0, Sìnce it is an odd function

II. Read the following text and answer the following questions on the basis of the same:
\(\int e^{x}\left[f(x)+f^{\prime}(x)\right] d x\) = \(\int e^{x} f(x) d x+\int e^{x} f^{\prime}(x) d x\)
= \(f(x) e^{x}-\int f^{\prime}(x) e^{x} d x\) + \(\int f^{\prime}(x) e^{x} d x\)
= \(e^{x} f(x)+c\)

Question 1.
\(\int e^{x}(\sin x+\cos x) d x\) = …………..
(A) e^x cos x + C
(B) e^x sin x + C
(C) e^x + C
(D) e^x(-cos x + sin x) + c
Answer:
(B) e^x sin x + C

Explanation:
\(\int e^{x}(\underbrace{\sin x}_{f(x)}+\underbrace{\cos x}_{f^{\prime}(x)}) d x=e^{x} \sin x+c\)

Question 2.
\(\int e^{x}\left(\frac{x-1}{x^{2}}\right) d x\) dx = …………..
(A) e^x + C
(B) \(\frac{e^{x}}{x}+c\)
(C) \(\frac{e^{x}}{x^{2}}+c\)
(D) \(\frac{-e^{x}}{x^{2}}+c\)
Answer:
(B) \(\frac{e^{x}}{x}+c\)

Explanation:
\(\int e^{x}\left(\frac{x-1}{x^{2}}\right) d x\) = \(\int e^{x}\left(\frac{\frac{1}{x}}{\frac{x}{f(x)}}-\frac{\frac{1}{x^{2}}}{f^{\prime}(x)}\right) d x\)
= \(\frac{e^{x}}{x}+c\)

Question 3.
\(\int e^{x}(x+1) d x\) = …………….
(A) x e^x + C
(B) e^x + C
(C) e^x + C
(D) None of these
Answer:
(A) x e^x + C

Explanation:
\(\int e^{x}\left(\underset{f(x)}{x}+\underset{f^{\prime}(x)}{1}\right) d x=x e^{x}+c\)

Question 4.
\(\int_{0}^{\pi} e^{x}\left(\tan x+\sec ^{2} x\right) d x\) = …………..
(A) 0
(B) 1
(C) -1
(D) -e^x
Answer:
(A) 0

Explanation:
\(\int_{0}^{\pi} e^{x}\left(\tan x+\sec ^{2} x\right) d x=\left[e^{x} \tan x\right]_{0}^{\pi}=0\)

Question 5.
\(\int \frac{x e^{x}}{(1+x)^{2}}\) = …………..
(A) \(x e^{x}+c\)
(B) \(\frac{e^{x}}{(x+1)^{2}}+c\)
(C) \(\frac{x e^{x}}{x+1}+c\)
(D) \(\frac{e^{x}}{x+1}+c\)
Answer:
(D) \(\frac{e^{x}}{x+1}+c\)

Explanation:
\(\int e^{x}\left[\frac{(x+1)-1}{(x+1)^{2}}\right] d x\) = \(\int e^{x}\left[\frac{1}{x+1}-\frac{1}{(x+1)^{2}}\right] d x\)
= \(\frac{e^{x}}{x+1}+c\)

III. Read the following text and answer the following questions on the basis of the same:

Let’s say that we want to evaluate \(\int[P(x) / Q(x)]\) where P(x) is a proper rational fraction. In such cases, it is possible to write the integrand as a sum of simpler rational functions by using partial fraction decomposition. Post this, integration can be carried out easily. The following image indicates some simple partial fractions which can be associated with various rational functions:

In the above table, A, B and C are real numbers to be determined suitably.

Question 1.
\(\frac{e^{x}}{x+1}+c\)
(A) log\(\frac{e^{x}}{x+1}+c\) + C
(B) 1og\(\frac{e^{x}}{x+1}+c\) + C
(C) log\(\frac{e^{x}}{x+1}+c\) + C
(D) log\(\frac{e^{x}}{x+1}+c\) + C
Answer:
(A) log\(\frac{e^{x}}{x+1}+c\) + C

Explanation:
We write,
\(\frac{1}{(x+1)(x+2)}\) = \(\frac{A}{x+1}+\frac{B}{x+2}\) ………(i)
where; real number A and B are to be determined suitably. This gives
1 = A(x + 2) + B(x + 1)
Equating the coefficients of x and the constant term, we get
A + B = 0 and 2A + B = 1
Solving these equatlons,we get A = 1 and B = -1.
Thus, the Integrand Is given by
\(\frac{1}{(x+1)(x+2)}\) = \(\frac{1}{x+1}+\frac{-1}{x+2}\)
Therefore,
\(\int \frac{d x}{(x+1)(x+2)}=\int \frac{d x}{x+1}-\int \frac{d x}{x+2}\)
= \(\log |x+1|-\log |x+2|+C\)
= \(\log \left|\frac{x+1}{x+2}\right|+C\)

Question 2.
Integration of (x + 1)(x +2)
(A) log \(\frac{(x+1)^{2}}{(x+2)}\) + C
(B) log \(\frac{(x+2)^{2}}{(x+1)}\) + C
(C) log \(\frac{(x)^{2}}{(x+1)}\) + C
(D) log \(\frac{(x-2)^{2}}{(x+1)}\) + C
Answer:
(B) log \(\frac{(x+2)^{2}}{(x+1)}\) + C

Explanation:
Let
\(\frac{x}{(x+1)(x+2)}=\frac{A}{(x+1)}+\frac{B}{(x+2)}\)
⇒ x = A(x + 2) + B(x + 1)
Equating the coefficients of x and constant term, we obtain
A + B = 1
2A + B = 0
On solving, we obtain
A = -1 and B = 2
\(\frac{x}{(x+1)(x+2)}=\frac{-1}{(x+1)}+\frac{2}{(x+2)}\)
⇒ \(\int \frac{x}{(x+1)(x+2)} d x=\int \frac{-1}{(x+1)}+\frac{2}{(x+2)} d x\)
= – log |x + 1| + 2 log |x + 2| + C
= log(x + 2)² – 1og |x + 1|+ C
= log \(\frac{(x+2)^{2}}{(x+1)}\) + C

Question 3.
\(\int \frac{1}{x^{2}-9}\)dx
(A) \(\frac{1}{6} \log \left|\frac{x-3}{x+3}\right|+C\)
(B) \(\frac{1}{6} \log \left|\frac{x-2}{x+3}\right|+C\)
(C) \(\frac{1}{6} \log \left|\frac{x+3}{x-3}\right|+C\)
(D) \(\frac{1}{3} \log \left|\frac{x-3}{x+3}\right|+C\)
Answer:
(A) \(\frac{1}{6} \log \left|\frac{x-3}{x+3}\right|+C\)

Explanation:
Let
\(\frac{1}{(x+3)(x-3)}=\frac{A}{(x+3)}+\frac{B}{(x-3)}\)
I = A(x – 3)+B(x + 3)
Equating the coefficients of x and constant term, we obtain
A + B = 0
-3A + 3B = 1
On solving, we obtain
A = –\(\frac{1}{6}\) and B = \(\frac{1}{6}\)
∴ \(\frac{1}{(x+3)(x-3)}=\frac{-1}{6(x+3)}+\frac{1}{6(x-3)}\)
⇒ \(\int \frac{1}{\left(x^{2}-9\right)} d x=\int\left(\frac{-1}{6(x+3)}+\frac{1}{6(x-3)}\right) d x\)
= \(-\frac{1}{6} \log |x+3|+\frac{1}{6} \log |x-3|\) + C
= \(\frac{1}{6} \log \left|\frac{(x-3)}{(x+3)}\right|+C\)

Question 4.
\(\int \frac{1}{e^{x}-1} d x\)
(A) 1og\(\left|\frac{e^{x}-1}{2}\right|\) + C
(B) 1og\(\left|\frac{e^{x}-1}{2 e^{x}}\right|\) + C
(C) log\(\left|\frac{e^{x}-1}{2 x}\right|\) + C
(D) log\(\left|\frac{e^{x}-1}{e^{x}}\right|\) + C
Answer:
(D) log\(\left|\frac{e^{x}-1}{e^{x}}\right|\) + C

Explanation:
Let
e^x = t
⇒ e^x dx = dt
⇒ \(\int \frac{1}{e^{x}-1} d x=\int \frac{1}{t-1} \times \frac{d t}{t}\)
= \(\int \frac{1}{t(t-1)} d t\)
Let \(\frac{1}{t(t-1)}=\frac{A}{t}+\frac{B}{t-1}\)
1 = A(t – 1) + Bt ………..(i)
Substituting t = 1 and t = O in equation (i), we obtain
A = -1 and B = 1
∴\(\frac{1}{t(t-1)}=\frac{-1}{t}+\frac{1}{t-1}\)
⇒ \(\int \frac{1}{t(t-1)} d t=\log \left|\frac{t-1}{t}\right|+C\)
= \(\log \left|\frac{e^{x}-1}{e^{x}}\right|+C\)

Question 5.
\(\int \frac{d x}{x\left(x^{2}+1\right)}\) =
(A) \(\log |x|+\frac{1}{2} \log \left|x^{2}+1\right|+C\)
(B) \(\log |x|-\frac{1}{4} \log \left|x^{2}+1\right|+C\)
(C) \(\log |x|-\frac{1}{2} \log \left|x^{2}+1\right|+C\)
(D) \(\log |x|-\frac{1}{3} \log \left|x^{2}-1\right|+C\)
Answer:
(C) \(\log |x|-\frac{1}{2} \log \left|x^{2}+1\right|+C\)

Explanation:
Let
\(\frac{1}{x\left(x^{2}+1\right)}=\frac{A}{x}+\frac{B x+C}{x^{2}+1}\)
1 = A(x² + 1) + (Bx + C)x
Equating the coefficients of x², x and constant
term, we obtain
A + B = 0
C = 0
A = 1
On solving these equations, we obtain
A =1, B = -1, and C = 0
∴ \(\frac{1}{x\left(x^{2}+1\right)}=\frac{1}{x}+\frac{-x}{x^{2}+1}\)
⇒ \(\int \frac{1}{x\left(x^{2}+1\right)} d x=\int\left\{\frac{1}{x}-\frac{x}{x^{2}+1}\right\} d x\)
= \(\log |x|-\frac{1}{2} \log \left|x^{2}+1\right|+C\)

MCQ Questions for Class 12 Maths with Answers

Check the below NCERT MCQ Questions for Class 12 Physics Chapter 15 Communication Systems with Answers Pdf free download. MCQ Questions for Class 12 Physics with Answers were prepared based on the latest exam pattern. We have provided Communication Systems Class 12 Physics MCQs Questions with Answers to help students understand the concept very well. https://mcqquestions.guru/mcq-questions-for-class-12-physics-chapter-15/

Communication Systems Class 12 MCQs Questions with Answers

MCQ On Communication System Class 12 Pdf Question 1.
Who undertook the first space walk and in which year?
(a) Leonov 1965
(b) Neil Armstrong, 1969
(c) Rakesh Sharma. 1998
(d) None of these

MCQ On Communication System Class 12 Chapter 15 Question 2.
The term used “to collect the information about an object and a place without physical contact” is called :
(a) modulation
(b) communication
(c) amplification
(d) remote sensing

Communication System Class 12 MCQ Chapter 15 Question 3.
The velocity of electromagnetic wave is:
(a) 3 × 10⁵ ms^-1
(b) 3 × 10⁶ ms^-1
(c) 3 × 10⁸ ms^-1
(d) 3 × 10¹⁰ ms^-1

Chapter 15 Physics Class 12 MCQs Question 4.
The audio frequencies range from:
(a) 20 Hz to 20.000 kHz
(b) 20 Hz to 20 kHz
(c) 20 kHz to 20.000 kHz
(d) None of these

Communication System MCQ Pdf Class 12 Question 5.
The wavelength of a wave of frequency 10 kHz is:
(a) 30 m
(b) 300 m
(c) 30 km
(d) 300 km

Question 6.
The area served by an antenna of height 100 m is:
(a) 10⁹m²
(b) 4 × 10⁹ m²
(c) 6 × 10⁹m²
(d) 8 × 10¹⁰m²

Question 7.
Which of the following is not transducer?
(a) Loudspeaker
(b) Amplifier
(c) Microphone
(d) All

Question 8.
The space waves which are affected seriously by atmospheric conditions are:
(a) MF
(b) HUF
(c) VHF
(d) UHF

Question 9.
An antenna is:
(a) Inductive
(b) Capacitive
(c) Resistive
(d) A transformer

Question 10.
Broadcasting antenna are generally:
(a) Ommi directional type
(b) Vertical type
(c) Horizontal type
(d) None

Question 11.
The modulation index in amplitude modulation is:
(a) Always zero
(b) Between 0 and 1
(c) Between 1 and ∞
(d) None of these

Question 12.
The output of a digital computer is an example of:
(a) digital signal
(b) analog signal
(c) both (a) and (b)
(d) neither (a) nor (b)

Question 13.
Name the man who was first to place his foot on the moon and in which year:
(a) Neil Armstrong, 1969
(b) James Van A lien, 1971
(c) Leonov, 1965
(d) None of these

Question 14.
A microphone converts:
(a) sound signals into electrical signals
(b) electrical signals into sound signals
(c) both (a) and (b)
(d) Neither (a) nor (b)

Question 15.
A loudspeaker converts:
(a) electrical signals into sound signals
(b) sound signals into electrical signals
(c) both (a) and (b)
(d) neither (a) nor (b)

Question 16.
The sound produced by a tuning fork is a sort of:
(a) analog signal
(b) digital signal
(c) both (a) and (b)
(d) neither (a) nor (b)

Question 17.
The length of a half wave dipole at 30 mega-hertz is:
(a) 5 m
(b) 10 m
(c) 25 m
(d) 80 m

Question 18.
In space communication, the sound waves can be sent from one place to another:
(a) through space
(b) through wires
(c) by superimposing it on undamped electro-magnetic waves
(d) by superimposing it on damped electro-magnetic waves

Question 19.
The output of a digital computer is an example of:
(a) digital signal
(b) analog signal
(c) both (a) and (b) above
(d) neither (a) nor (b)

Question 20.
Which is more advantageous?
(a) analog data communication
(b) digital data communication
(c) both (a) and (b) are equally good
(d) depends on the situation

Question 21.
Communication channel consists of:
(a) transmission line only
(b) optical fibre only
(c) free space only
(d) All of the above

Question 22.
AM is used for broadcasting because:
(a) it is more noise immune than other modulation system
(b) it requires less transmitting power compare with other systems
(c) its use avoids receiver complexity
(d) No other modulation system can provide the necessary bandwidth faithful transmission

Question 23.
Digital signals:
(a) represents values as discrete steps
(b) Do not represents values as discrete steps
(c) represent values steps
(d) represent random steps

Question 24.
Digital signals:
(a) deal with all sort of values
(b) can use decimal system
(c) can use binary system
(d) (b) and (c) both

Question 25.
Increase in frequency deviation results into:
(a) increase in noise of FM receiver
(b) decrease in noise of AM receiver
(c) increase in noise of Am receiver
(d) decrease in noise of FM receiver

We hope the given NCERT MCQ Questions for Class 12 Physics Chapter 15 Communication Systems with Answers Pdf free download will help you. If you have any queries regarding Communication Systems CBSE Class 12 Physics MCQs Multiple Choice Questions with Answers, drop a comment below and we will get back to you soon.