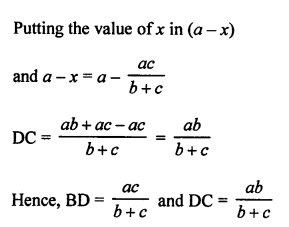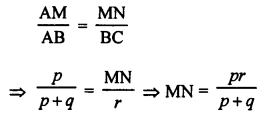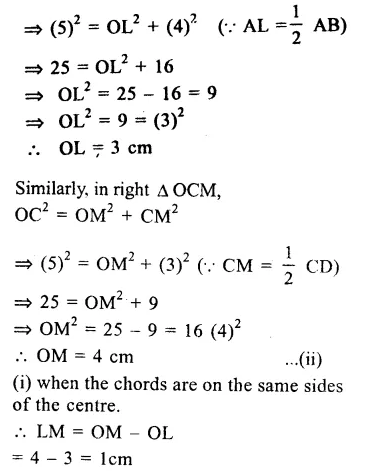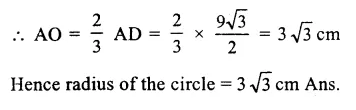Prasanna

RS Aggarwal Class 10 Solutions Chapter 4 Triangles Ex 4E

These Solutions are part of RS Aggarwal Solutions Class 10. Here we have given RS Aggarwal Solutions Class 10 Chapter 4 Triangles Ex 4E.

Other Exercises

• RS Aggarwal Solutions Class 10 Chapter 4 Triangles Ex 4A
• RS Aggarwal Solutions Class 10 Chapter 4 Triangles Ex 4B
• RS Aggarwal Solutions Class 10 Chapter 4 Triangles Ex 4C
• RS Aggarwal Solutions Class 10 Chapter 4 Triangles Ex 4D
• RS Aggarwal Solutions Class 10 Chapter 4 Triangles Ex 4E
• RS Aggarwal Solutions Class 10 Chapter 4 Triangles MCQS
• RS Aggarwal Solutions Class 10 Chapter 4 Triangles Test Yourself

Very-Short-Answer and Short-Answer Questions
Question 1.
Solution:
Two properties for similarity of two triangles are:
(i) Angle-Angle-Angle (AAA) property.
(ii) Angle-Side-Angle (ASA) property.

Question 2.
Solution:
In a triangle, if a line parallel to one side is drawn, it will divide the other two sides proportionally.

Question 3.
Solution:
If a line divides any two sides of a triangle in the same ratio. Then, the line must be parallel to the third side.

Question 4.
Solution:
The line joining the midpoints of two sides of a triangle, is parallel to the third side.

Question 5.
Solution:
In two triangles, if three angles of the one triangle are equal to the three angles of the other, the triangles are similar.

Question 6.
Solution:
In two triangles, if two angles of the one triangle are equal to the corresponding angles of the other triangle, then the triangles are similar.

Question 7.
Solution:
In two triangles, if three sides of the one are proportional to the corresponding sides of the other, the triangles are similar.

Question 8.
Solution:
In two triangles, if two sides of the one are proportional to the corresponding sides of the other and their included angles are equal, the two triangles are similar.

Question 9.
Solution:
In a right angled triangle, the square on the hypotenuse is equal to the sum of squares on the other two sides.

Question 10.
Solution:
In a triangle, if the square on the longest side is equal to the sum of the squares on the other two sides, then the angle opposite to the hypotenuse is a right angle.

Question 11.
Solution:
The ratio of their areas will be 1 : 4.

Question 12.
Solution:
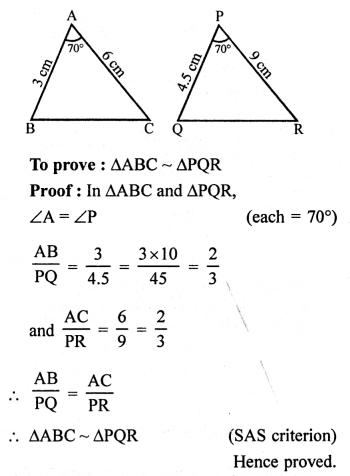
In two triangles ∆ABC and ∆PQR,
AB = 3 cm, AC = 6 cm, ∠A = 70°
PR = 9 cm, ∠P = 70° and PQ= 4.5 cm

Question 13.
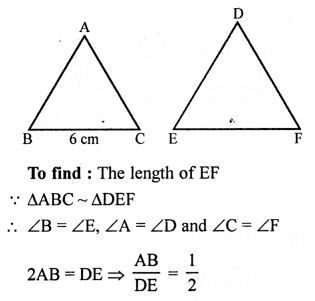
Solution:
∆ABC ~ ∆DEF
2AB = DE, BC = 6 cm

Question 14.
Solution:
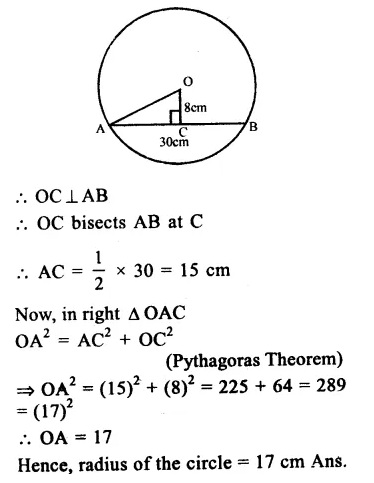
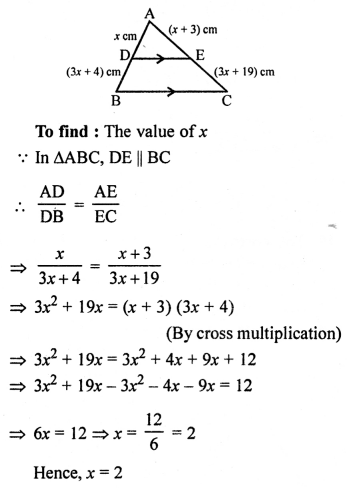
In the given figure,
DE || BC
AD = x cm, DB = (3x + 4) cm
AE = (x + 3) cm and EC = (3x + 19) cm

Question 15.
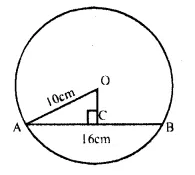
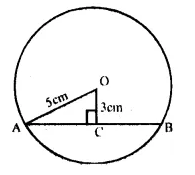
Solution:
AB is the ladder and A is window.
AB =10 m, AC = 8 m

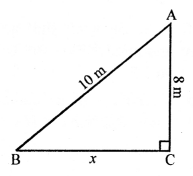
We have to find the distance of BC
Let BC = x m
In right ∆ABC,
AB² = AC² + BC² (Pythagoras Theorem)
(10)² = 8² + x²
⇒ 100 = 64 + x²
⇒ x² = 100 – 64 = 36 = (6)²
x = 6
Distance between foot of ladder and base of the wall = 6 m.

Question 16.
Solution:
∆ABC is an equilateral triangle with side = 2a cm
AD ⊥ BC
and AD bisects BC at D

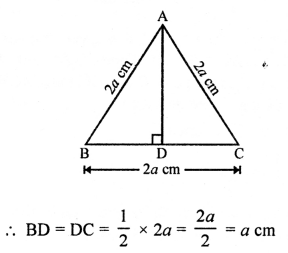
Now, in right ∆ABD,
AB² = AD² + BD² (Pythagoras Theorem)
⇒ (2a)² = AD² + (a)²
⇒ 4a² = AD² + a²
⇒ AD² = 4a² – a² = 3a²
AD = √3 a² = √3 a cm

Question 17.
Solution:
Given : ∆ABC ~ ∆DEF
and ar (∆ABC) = 64 cm²
and ar (∆DEF) = 169 cm², BC = 4 cm.

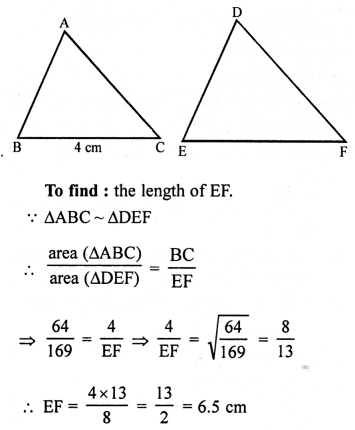
Question 18.
Solution:
In trape∠ium ABCD,
AB || CD
AB = 2CD
Diagonals AC and BD intersect each other at O
and area(∆AOB) = 84 cm².

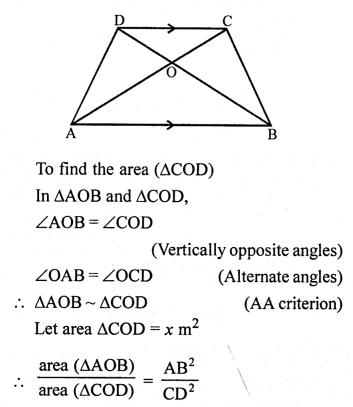
Question 19.
Solution:
Let ∆ABC ~ ∆DEF

Question 20.
Solution:
In an equiangular ∆ABC,
AB = BC = CA = a cm.
Draw AD ⊥ BC which bisects BC at D.

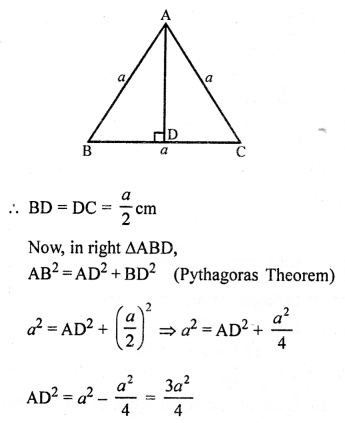
Question 21.
Solution:
ABCD is a rhombus whose sides are equal and diagonals AC and BD bisect each other at right angles.

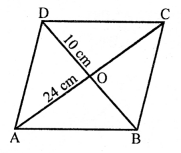
∠AOB = 90° and AO = OC, BO = OD
AO = \(\frac { 24 }{ 2 }\) = 12 cm
and BO = \(\frac { 10 }{ 2 }\) = 5 cm
Now, in right ∆AOB,
AB² = AO² + BO² (Pythagoras Theorem)
= (12)² + (5)² = 144 + 25 = 169 = (13)²
AB = 13
Each side of rhombus = 13 cm

Question 22.
Solution:
∆DEF ~ ∆GHK
∠D = ∠G = 48°
∠E = ∠H = 57°
∠F = ∠K

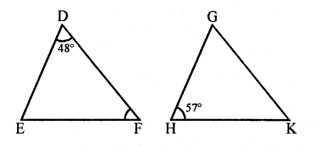
Now, in ∆DEF,
∠D + ∠E + ∠F = 180° (Angles of a triangle)
⇒ 48° + 57° + ∠F = 180°
⇒ 105° + ∠F= 180°
⇒ ∠F= 180°- 105° = 75°

Question 23.
Solution:
In the given figure,
In ∆ABC,
MN || BC
AM : MB = 1 : 2

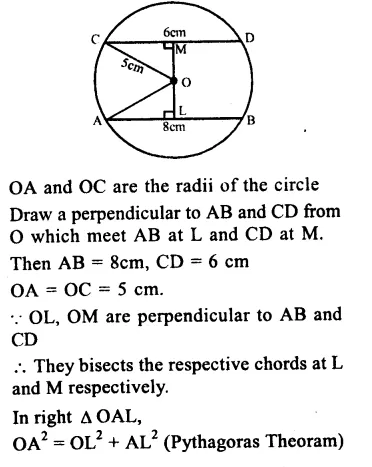
Question 24.
Solution:
In ∆BMP,
PB = 5 cm, MP = 6 cm and BM = 9 cm
and in ∆CNR, NR = 9 cm

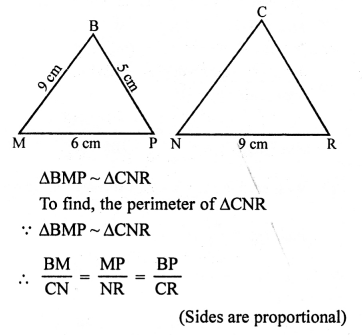
Question 25.
Solution:
In ∆ABC,
AB = AC = 25 cm
BC = 14 cm

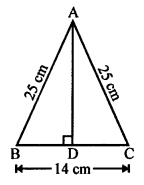
AD ⊥ BC which bisects the base BC at D.
BD = DC = \(\frac { 14 }{ 2 }\) = 7 cm
Now, in right ∆ABD,
AB² = AD² + BD² (Pythagoras Theorem)
(25)² = AD² + 7²
625 = AD² + 49
⇒ AD² = 625 – 49 = 576
⇒ AD² = 576 = (24)²
AD = 24 cm
Length of altitude = 24 cm

Question 26.
Solution:
A man goes 12 m due north of point O reaching A and then 37 m due west reaching B.

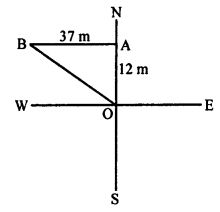
Join OB,
In right ∆OAB,
OB² = OA² + AB² (Pythagoras Theorem)
= (12)² + (35)² = 144 + 1225 = 1369 = (37)²
OB = 37 m
The man is 37 m away from his starting point.

Question 27.
Solution:
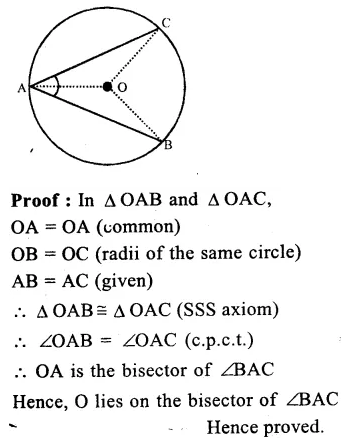
In ∆ABC, AD is the bisector of ∠A which meets BC at D.
AB = c, BC = a, AC = b

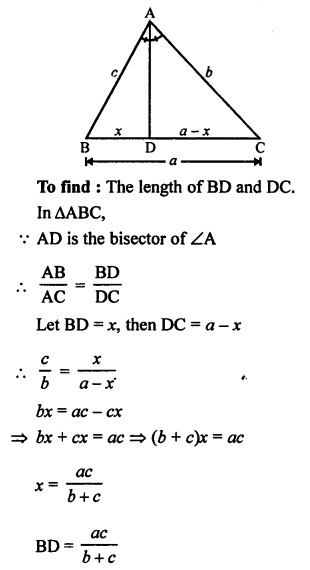
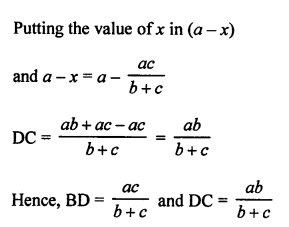
Question 28.
Solution:
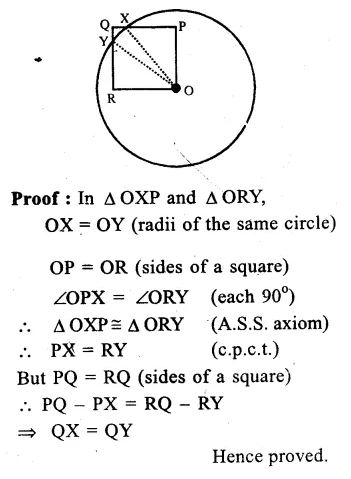
In the given figure, ∠AMN = ∠MBC = 76°
p, q and r are the lengths of AM, MB and BC Express the length of MN in terms of p, q and r.
In ∆ABC,
∠AMN = ∠MBC = 76°
But there are corresponding angles
MN || BC
∆AMN ~ ∆ABC

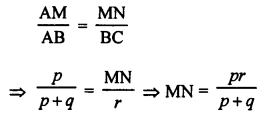
Question 29.
Solution:
In rhombus ABCD,
Diagonals AC and BD bisect each other at O at right angles.

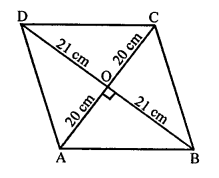
AO = OC = \(\frac { 40 }{ 2 }\) = 20 cm
BO = OD = \(\frac { 42 }{ 2 }\) = 21 cm
Now, in right ∆AOB,
AB2 = AO2 + BO2 = (20)2 + (21)2 = 400 + 441 = 841
AB = √841 cm = 29 cm

Each side of rhombus = 29 cm

For each of the following statements state whether true (T) or false (F):
Question 30.
Solution:
(i) True.
(ii) False, as sides will not be proportion in each case.
(iii) False, as corresponding sides are proportional, not necessarily equal.
(iv) True.
(v) False, in ∆ABC,
AB = 6 cm, ∠A = 45° and AC = 8 cm

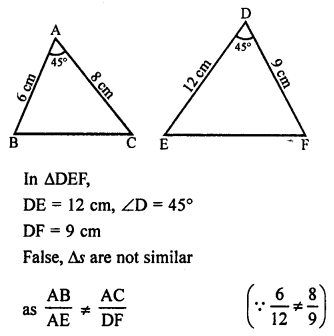
(vi) False, the polygon joining the midpoints of a quadrilateral is not a rhombus but it is a parallelogram.
(vii) True.
(viii) True.
(ix) True, O is any point in rectangle ABCD then
OA² + OC² = OB² + OD² is true.

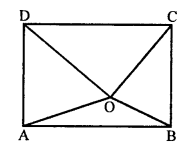
(x) True.

Hope given RS Aggarwal Solutions Class 10 Chapter 4 Triangles Ex 4E are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 9 Solutions Chapter 11 Circle Ex 11A

These Solutions are part of RS Aggarwal Solutions Class 9. Here we have given RS Aggarwal Solutions Class 9 Chapter 11 Circle Ex 11A.

Other Exercises

• RS Aggarwal Solutions Class 9 Chapter 11 Circle Ex 11A
• RS Aggarwal Solutions Class 9 Chapter 11 Circle Ex 11B
• RS Aggarwal Solutions Class 9 Chapter 11 Circle Ex 11C

Question 1.
Solution:
Let AB be a chord of a circle with centre O. OC⊥AB and OA be the radius of the circle, then
AB = 16cm, OA = 10cm .

OC ⊥ AB.
OC bisects AB at C
AC = \(\frac { 1 }{ 2 } \) AB = \(\frac { 1 }{ 2 } \) x 16 = 8cm

Question 2.
Solution:
Let AB be the chord of the circle with centre O and OC ⊥ AB, OA be the radius of the circle,
then OC = 3cm, OA = 5cm

Now in right ∆ OAC,
OA² = AC² = OC² (Pythagoras Theorem)

Question 3.
Solution:
Let AB be the chord, OA be the radius of
the circle OC ⊥ AB
then AB = 30 cm, OC = 8cm

Question 4.
Solution:
AB and CD are parallel chords of a circle with centre O.

Question 5.
Solution:
Let AB and CD be two chords of a circle with centre O.
OA and OC are the radii of the circle. OL⊥AB and OM⊥CD.

Question 6.
Solution:
In the figure, a circle with centre O, CD is its diameter AB is a chord such that CD⊥AB.
AB = 12cm, CE = 3cm.
Join OA.
∵ COD⊥AB which intersects AB at E

Question 7.
Solution:
A circle with centre O, AB is diameter which bisects chord CD at E
i.e. CE = ED = 8cm and EB = 4cm
Join OC.
Let radius of the circle = r

Question 8.
Solution:
Given : O is the centre of a circle AB is a chord and BOC is the diameter. OD⊥AB
To prove : AC || OD and AC = 20D
Proof : OD⊥AB
∵ D is midpoint of AB

Question 9.
Solution:
Given : O is the centre of the circle two
chords AB and CD intersect each other at P inside the circle. PO bisects ∠BPD.
To prove : AB = CD.

Question 10.
Solution:
Given : PQ is the diameter of the circle with centre O which is perpendicular to one chord AB and chord AB || CD.
PQ intersects AB and CD at E and F respectively
To prove : PQ⊥CD and PQ bisects CD.

Question 11.
Solution:
Two circles with centre O and O’ intersect each other.

To prove : The two circles cannot intersect each other at more than two points.
Proof : Let if opposite, the two circles intersect each other at three points P, Q and R.
Then these three points are non-collinear. But, we know that through three non- collinear points, one and only one circle can be drawn.
∵ Our supposition is wrong
Hence two circle can not intersect each other at not more than two points.
Hence proved

Question 12.
Solution:
Given : Two circles with centres O and O’ intersect each other at A and B. AB is a common chord. OO’ is joined.
AO and AO is joined.

Question 13.
Solution:
Given : Two equal circles intersect each other at P and Q.
A straight line drawn through
P, is drawn which meets the circles at A and B respectively
To prove : QA = QB

Question 14.
Solution:
Given : A circle with centre 0. AB and CD are two chords and diameter PQ bisects AB and CD at L and M
To Prove : AB || CD.

Question 15.
Solution:
Given : Two circles with centres A and B touch each other at C internally. A, B arc joined. PQ is the perpendicular bisector of AB intersecting it at L and meeting the bigger circle at P and Q respectively and radii of the circles are 5cm and 3cm. i.e. AC = 5cm,BC = 3cm
Required : To find the lenght of PQ

Question 16.
Solution:
Given : AB is a chord of a circle with centre O. AB is produced to C such that BC = OB, CO is joined and produced to meet the circle at D.
∠ ACD = y°, ∠ AOD = x°
To prove : x = 3y

Question 17.
Solution:
Given : O is the centre of a circle AB and AC are two chords such that AB = AC
OP⊥AB and OQ⊥AC.
which intersect AB and AC at M and N
respectively. PB and QC are joined.
To prove : PB = QC.

Question 18.
Solution:
Given : In a circle with centre O, BC is its diameter. AB and CD are two chords such that AB || CD.
To prove : AB = CD
Const. Draw OL⊥AB
OM⊥CD.
Proof : In ∆ OLB and ∆ OCM,
OB = OC (radii of the same circle)
∠ OLB = ∠ OMC (each 90°)
∠ OBL = ∠ OCM (alternate angles)

Question 19.
Solution:
Equilateral ∆ ABC in inscribed in a circle in which
AB = BC = CA = 9cm.

Question 20.

Solution:
Given : AB and AC are two equal chords of a circle with centre O
To Prove : O lies on the bisector of ∠ BAC

Question 21.
Solution:
Given : OPQR is a square with centre O, a circle is drawn which intersects the square at X and Y.
To Prove : Q = QY
Const. Join OX and OY

Hope given RS Aggarwal Solutions Class 9 Chapter 11 Circle Ex 11A are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.