RS Aggarwal Class 10 Solutions Chapter 4 Triangles Ex 4B
These Solutions are part of RS Aggarwal Solutions Class 10. Here we have given RS Aggarwal Solutions Class 10 Chapter 4 Triangles Ex 4B.
Other Exercises
- RS Aggarwal Solutions Class 10 Chapter 4 Triangles Ex 4A
- RS Aggarwal Solutions Class 10 Chapter 4 Triangles Ex 4B
- RS Aggarwal Solutions Class 10 Chapter 4 Triangles Ex 4C
- RS Aggarwal Solutions Class 10 Chapter 4 Triangles Ex 4D
- RS Aggarwal Solutions Class 10 Chapter 4 Triangles Ex 4E
- RS Aggarwal Solutions Class 10 Chapter 4 Triangles MCQS
- RS Aggarwal Solutions Class 10 Chapter 4 Triangles Test Yourself
Question 1.
Solution:
We know that two triangles are similarity of their corresponding angles are equal and corresponding sides are proportional.
(i) In ∆ABC and ∆PQR
∠A = ∠Q = 50°
∠B = ∠P = 60° and ∠C = ∠R = 70°
∆ABC ~ ∆QPR (AAA axiom)
(ii) In ∆ABC and ∆DEF
In ∆ABC,
AB = 3 cm, BC = 4.5
and in ∆DEF
DF = 6 cm, DE = 9 cm
∆ABC is not similar to ∆DEF
As in ∆ABC, ∠A is not included of two sides AB and BC.
(iii) In ∆ABC and ∆PQR
In ∆ABC,
AC = 8 cm BC = 6 cm
Included ∠C = 80°
In ∆PQR,
PQ = 4.5 cm, QR = 6 cm
and included ∠Q = 80°

(v) In ∆ABC,
∠A = 80°, ∠C = 70°
and third angle
∠B = 180° – (80° + 70°)
⇒ ∠B = 180° – 150° = 30°
In ∆MNR,
∠M = 80°, ∠N = 30°, and ∠R = [180° – (80° + 30°)]
∠R = 180° – 110° = 70°
Now, in ∆ABC
∠A = ∠M – 80°, ∠B = ∠N = 30°
and ∠C = ∠R = 70°
∆ABC ~ ∆MNR (AAA or AA axiom)
Question 2.
Solution:
In the given figure, ∆ODC ~ ∆OBA and ∠BOC =115°, ∠CDO = 70°
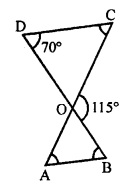
To find :
(i) ∠DOC
(ii) ∠DCO
(iii) ∠OAB
(iv) ∠OBA
∆ODC ~ ∆OBA
∠D = ∠B = 70°
∠C = ∠A
∠COD = ∠AOB
(i) But ∠DOC + ∠BOC = 180° (Linear pair)
⇒ ∠DOC + 115°= 180°
⇒ ∠DOC = 180° – 115° = 65°
(ii) ∠DOC + ∠CDO + ∠DCO = 180° (Angles of a triangle)
⇒ 65° + 70° + ∠DCO = 180°
⇒ 135° + ∠DCO = 180°
⇒ ∠DCO = 180° – 135°
∠DCO = 45°
(iii) ∠AOB = ∠DOC = 65° (vertically opposite angles)
∠OAB = ∠DCO = 45° (∆ODC ~ ∆OBA)
(iv) ∠OBA = ∠CDO = 70° (∆ODC ~ ∆OBA)
Question 3.
Solution:
In the given figure, ∆OAB ~ ∆OCD
AB = 8 cm, BO = 6.4 cm OC = 3.5 cm, CD = 5 cm
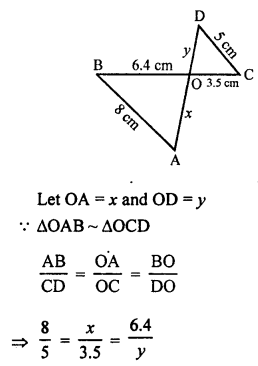
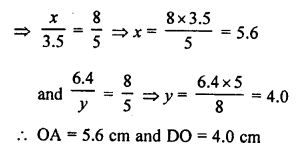
Question 4.
Solution:
Given : In the given figure,
∠ADE = ∠B
To prove:
(i) ∆ADE ~ ∆ABC
(ii) If AD = 3.8 cm, AE = 3.6 cm, BE = 2.1 cm and BC = 4.2 cm, find DE
Proof: (i) In ∆ADE and ∆ABC
∠ADE = ∠B (given)
∠A = ∠A (common)
∆ADE ~ ∆ABC (AA axiom)

Question 5.
Solution:
∆ABC ~ ∆PQR,
PQ = 12 cm
To find AB.
Perimeter of ∆ABC = AB + BC + CA = 32 cm
Perimeter of ∆PQR = PQ + QR + RP = 24 cm
Now,
∆ABC ~ ∆PQR
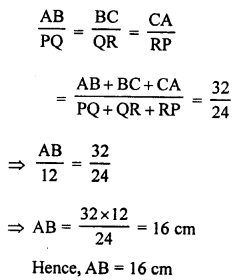
Question 6.
Solution:
∆ABC ~ ∆DEF
BC = 9.1 cm, EF = 6.5 cm
Perimeter of ∆DEF = 25 cm
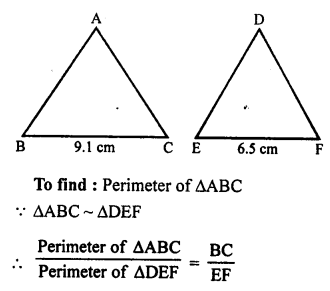

Question 7.
Solution:
Given : In the given figure,
∠CAB = 90° and AD ⊥ BC
To prove : ∆BDA ~ ∆BAC
If AC = 75 cm, AB = 1 m or 100 cm,
BC = 1.25 m or 125 cm
Find AD.
∆BDA ~ ∆BAC (corresponding sides and proportional)

Question 8.
Solution:
In the given figure,
∠ABC = 90°, BD ⊥ AC.
AB = 5.7 cm, BD = 3.8 cm, CD = 5.4 cm
To find BC,
In ∆ABC and ∆BDC,
∠ABC = ∠BDC (each 90°)
∠BCA = ∠BCD (common)
∆ABC ~ ∆BDC (AA axiom)
Corresponding sides are proportional
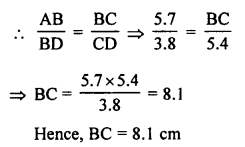
Question 9.
Solution:
In the given figure, ”
∠ABC = 90°, BD ⊥ AC
BD = 8 cm, AD = 4cm
To find CD,
Let CD = x
Now in ∆DBC and ∆BDA
∠BDC = ∠BDA (each 90°)
∠C = ∠ABD
∆DBC ~ ∆BDA
Sides are proportional
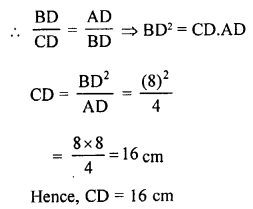
Question 10.
Solution:
In ∆ABC, P and Q are points on the sides AB and AC respectively such that
AP = 2 cm, PB = 4 cm, AQ = 3 cm and QC = 6 cm.
To prove : BC = 3 PQ
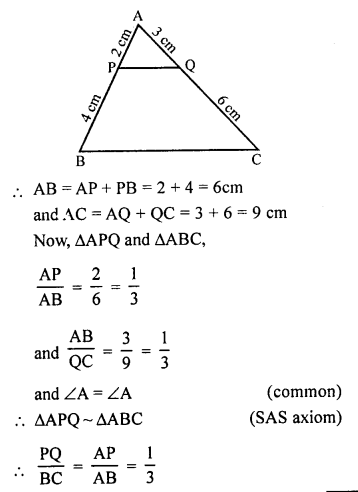
BC = 3 PQ
Hence proved.
Question 11.
Solution:
Given: ABCD is a parallelogram.
E is a point on BC and diagonal BD intersects AE at F.
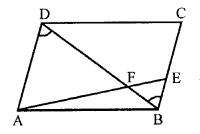
To prove : AF x FB = EF x FD
Proof: In ∆AFD and ∆BFE
∠AFD = ∠BFE (vertically opposite angles)
∠ADF = ∠FBE (alternate angles)
∆AFD ~ ∆BFE (AA axiom)
\(\frac { AF }{ EF }\) = \(\frac { FD }{ FB }\)
By cross multiplication,
⇒ AF x FB = EF x FD
Hence proved.
Question 12.
Solution:
Given : In the given figure,
DB ⊥ BC, DE ⊥ AB and AC ⊥ BC

Question 13.
Solution:
In ∆ABC and ∆DEF
AC is stick and BC is its shadow.
DF is the tower and EF is its shadow
AC = 7.5 m, BC = 5 m EF = 24 m,
let DF = x m
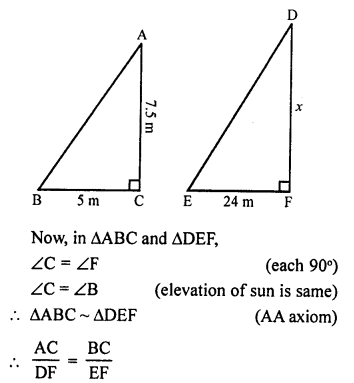

Question 14.
Solution:
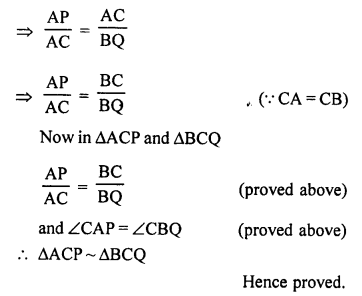
Given : In isosceles ∆ABC,
CA = CB, base AB and BA are produced in P and Q such that
AP x BQ = AC²
To prove : ∆ACP ~ ∆BCQ
Proof: In ∆ABC,
CA = CB
∠CAB = ∠CBA (Angles opposite to equal sides)
⇒ 180° – ∠CAB = 180° – ∠CBA (Subtracting each from 180°)
⇒ ∠CAP = ∠CBQ
AP x BQ = AC² (given)
Question 15.
Solution:
Given : In the given figure, ∠1 = ∠2

Question 16.
Solution:
Given : In quadrilateral ABCD,
AD = BC
P, Q, R and S are midpoints of AB, AC, CD and BD respectively.
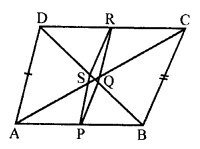
To proof : PQRS is a rhombus.
Proof: In ∆ABC,
P and Q are the midpoints of sides AB and AC respectively.
PQ || BC ……(i)

Question 17.
Solution:
In the given circle, two chords AB and CD intersect each other at P inside the circle.
To prove :
(a) ∆PAC ~ ∆PDB
(b) PA . PB = PC . PD
Proof:
(a) In ∆PAC and ∆PDB
∠APC = ∠BPD (Vertically opposite angles)
∠A = ∠D (Angles in the same segment)
∆PAC ~ ∆PDB (AA axiom)
\(\frac { PA }{ PD }\) = \(\frac { PC }{ PB }\)
⇒ PA x PB = PC x PD
Hence proved.
Question 18.
Solution:
In a circle, two chords AB and CD intersect each other at the point P outside the circle.
AC and BD are joined.
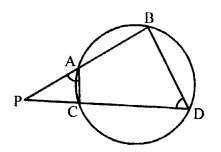
To prove :
(a) ∆PAC ~ ∆PDB
(b) PA . PB = PC . PD
Proof: In the circle, quadrilateral ABDC is a cyclic.
Ext. ∠PAC = ∠D
Now, in ∆PDB and ∆PAC
∠P = ∠P (common)
∠PAC = ∠D (proved)
∆PDB ~ ∆PAC (AA axiom)
or ∆PAC ~ ∆PBD
\(\frac { PA }{ PD }\) = \(\frac { PC }{ PB }\)
⇒ PA . PB = PC . PD
Hence proved
Question 19.
Solution:
Given : In right ∆ABC, ∠B = 90°
D is a point on hypotenuse AC such that
BD ⊥ AC and DP ⊥ AB and DQ ⊥ BC.
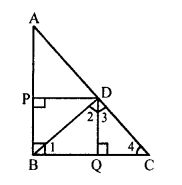
To prove :
(a) DQ² = DP . QC
(b) DP² = DQ . AP
Proof: AB ⊥ BC and DQ ⊥ BC
AB || DQ
DP ⊥ AB
DP || BC
Now, AB or PB || DQ and BC or BQ || DP BQDP is a rectangle
BQ = DP and BP = DQ
Now, in right ∆BQD
∠1 + ∠2 = 90° …..(i)
Similarly in rt. ∆DQC,
∠3 + ∠4 = 90° (DQ ⊥ BC) …(ii)
and in right ∆BDC,
∠2 + ∠3 = 90° …(iii)
∠BDC = 90° (BD ⊥ AC)
From (i) and (ii),
∠1 = ∠3
and from (ii) and (iii),
∠2 = ∠4
Now, in ∆BQD and ∆DQC
∠1 = ∠3
∠2 = ∠4 (proved)
∆BQD ~ ∆DQC (AA axiom)
\(\frac { BQ }{ DQ }\) = \(\frac { DQ }{ QC }\)
⇒ DQ² = BQ x QC
⇒ DQ² = DP x QC
(b) Similarly, we can prove that
∆PDA ~ ∆PBD
\(\frac { PD }{ PB }\) = \(\frac { AP }{ DP }\)
⇒ DP² = BP x AP
⇒ DP² = DQ . AP (BP = DQ)
Hence proved.
Hope given RS Aggarwal Solutions Class 10 Chapter 4 Triangles Ex 4B are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.