Prasanna

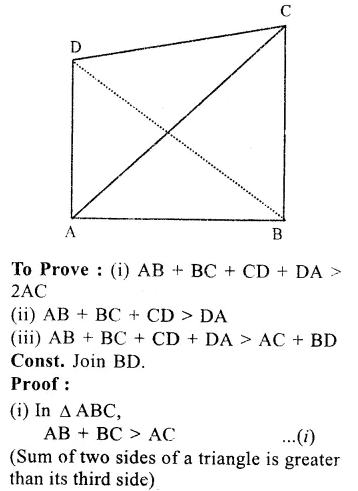
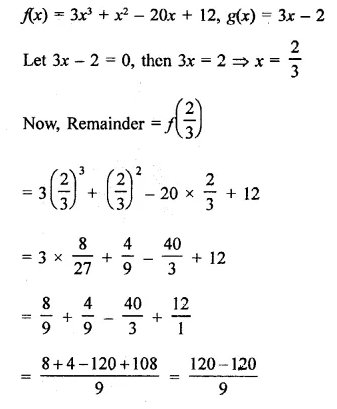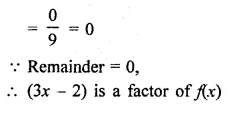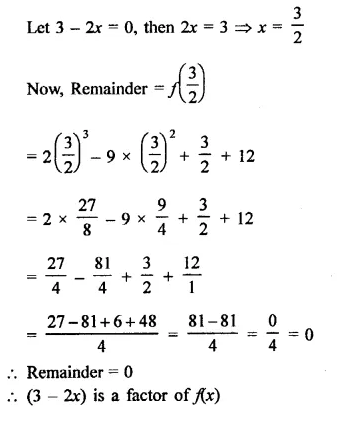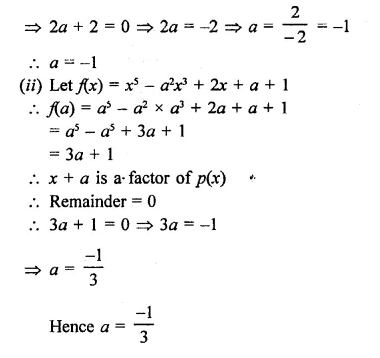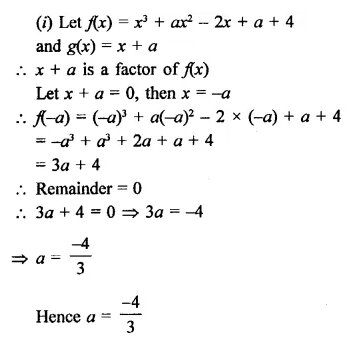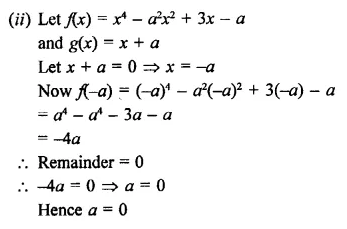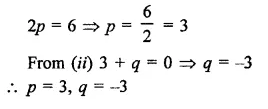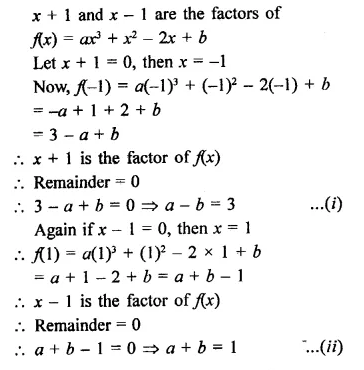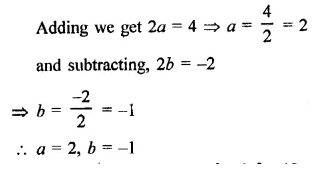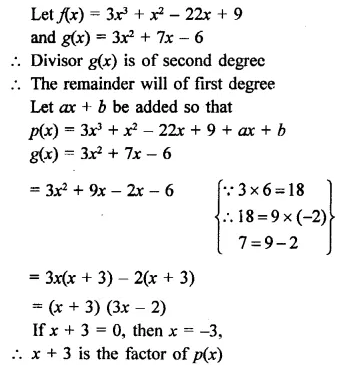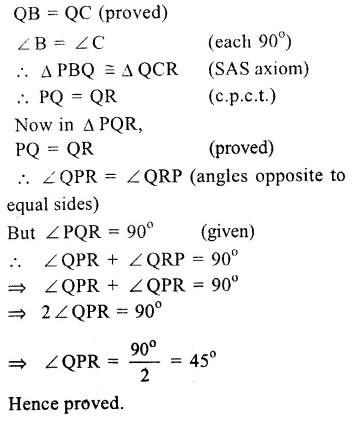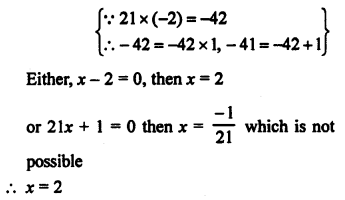RS Aggarwal Class 9 Solutions Chapter 9 Quadrilaterals and Parallelograms Ex 9B

These Solutions are part of RS Aggarwal Solutions Class 9. Here we have given RS Aggarwal Class 9 Solutions Chapter 9 Quadrilaterals and Parallelograms Ex 9B.

Other Exercises

• RS Aggarwal Solutions Class 9 Chapter 9 Quadrilaterals and Parallelograms Ex 9A
• RS Aggarwal Solutions Class 9 Chapter 9 Quadrilaterals and Parallelograms Ex 9B
• RS Aggarwal Solutions Class 9 Chapter 9 Quadrilaterals and Parallelograms Ex 9C

Question 1.
Solution:
In parallelogram ABCD.
∠ A = 72°
But ∠ A = ∠ C (opposite angle of a ||gm)
∴ ∠ C = 72°
∴ AD || BC
∴ ∠ A + ∠ B = 180° (co-interior angles)
=> 72° + ∠B = 180°
=> ∠B = 180° – 72°
=> ∠B = 108°
But ∠ B = ∠ D (opposite angles of a ||gm)
∴ ∠D = 108°
Hence ∠D = 108°, ∠ C = 72° and ∠ D = 108° Ans.

Question 2.
Solution:
In || gm ABCD, BD is its diagonal
and ∠DAB = 80° and ∠DBC = 60°
∴AB || DC
∴∠DAB + ∠ADC – 180°
(co-interior angles)
=> 80° + ∠ADC = 180°
=> ∠ ADC = 180° – 80°
=> ∠ ADC = 100°
But ∠ ADB = ∠ DBC (Alternate angles)
∴∠ ADB = 60°
But ∠ ADB + ∠ CDB = 100°
(∴∠ ADC = 100°)
60° + ∠CDB = 100°
=> ∠CDB = 100° – 60° = 40°
Hence ∠CDB = 40° and ∠ ADB = 60° Ans.

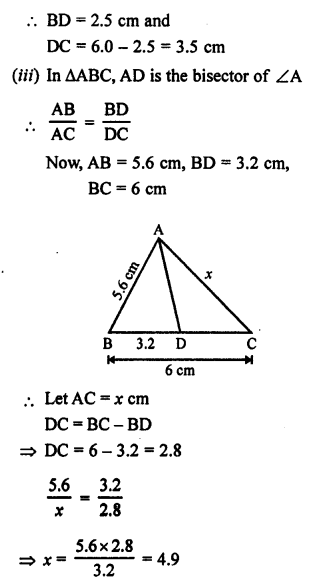
Question 3.
Solution:
Given : In ||gm ABCD,
∠ A = 60° Bisectors of ∠ A and ∠ B meet DC at P.
To Prove : (i) ∠APB = 90°
(ii) AD = DP and PB = PC = BC
(iii) DC = 2AD
Proof: ∴ AD || B (opposite sides of a ||gm)
∴∠ A + ∠ B = 180° (co-interior angles)
But AP and BP are the bisectors of ∠A and ∠B
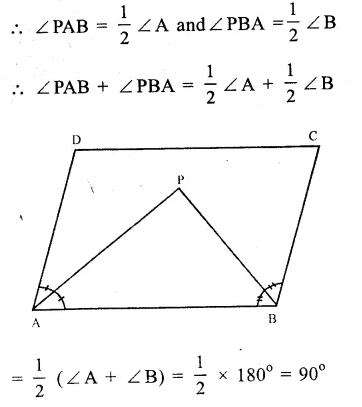
∴\(\frac { 1 }{ 2 } \)∠A + \(\frac { 1 }{ 2 } \) ∠B = 90°

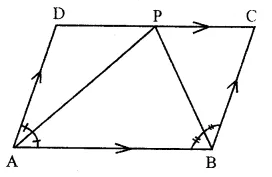
=> ∠PAB + ∠PBA = 90°
But in ∆ APB,
∠PAB + ∠PBA + ∠APB = 180° (angles of a triangle)
=> 90° + ∠APB = 180°
=> ∠APB = 180° – 90° = 90°
Hence ∠APB = 90°
(ii) ∠ A + ∠ D = 180° (co-interior angles)
and ∠ A – 60°
∴ ∠D = 180° – 60° = 120°
But ∠DAP = \(\frac { 1 }{ 2 } \) ∠A = \(\frac { 1 }{ 2 } \) x 60° = 30°
∴∠DPA = 180° – (∠DAP + ∠D)
= 180° – (30° + 120°)
= 180° – 150° = 30°
∠DAP = ∠DPA (each = 30°)
Hence AD = DP (sides opposite to equal angles)
In ∆ BCP,
∠ C = 60° (opposite to ∠ A)
∠CBP = \(\frac { 1 }{ 2 } \) ∠ B = \(\frac { 1 }{ 2 } \) x 120° = 60°
But ∠CPB + ∠CBP + ∠C = 180°
(Angles of a triangle)
=> ∠CPB + 60° + 60° = 180°
=> ∠CPB + 120° = 180°
=> ∠CPB = 180° – 120° = 60°
∆ CBP is an equilateral triangle and BC = CP = BP
=> PB – PC = BC
(iii) DC = DP + PC
= AD + BC
(∴ DP = AD and PC = BC proved)
= AD + AD (∴ AD = BC opposite sides of a ||gm)
= 2AD
Hence DC = 2AD.
Hence proved.

Question 4.
Solution:
In ||gm ABCD,
AC and BD are joined
∠BAO = 35°, ∠ DAO = 40°
∠COD = 105°
∴ ∠AOB = ∠COD
(vertically opposite angles)
∴∠AOB = 105°
(i) Now in ∆ AOB,
∠ABO + ∠AOB + ∠OAB = 180°
(angles of a triangle)
=> ∠ABO + 105° + 35° = 180°
=> ∠ABO + 140° = 180°
=> ∠ABO = 180° – 140°
∠ ABO = 40°
(ii) ∴ AB || DC
∴ ∠ ABO = ∠ ODC (alternate angles)
∴ ∠ ODC = 40°
(iii) ∴ AD || BC
∴ ∠ ACB = ∠ DAO or ∠ DAC
(alternate angles)
= 40°
(iv) ∴ ∠ A + ∠ B = 180° (co-interior angles)
=> (40° + 35°) + ∠B = 180°
=> ∠B = 180° – 75° = 105°
=> ∠ CBD + ∠ABO = 105°
=> ∠CBD + 40° = 105°
=> ∠CBD = 105° – 40° = 65°
Hence ∠ CBD = 65° Ans.

Question 5.
Solution:
In ||gm ABCD
( ∠A = (2x + 25)° and ∠ B = (3x – 5)°
∴AD || BC (opposite sides of parallelogram)
∴∠ A + ∠B = 180° (co-interior angles)
=> 2x + 25° + 3x – 5° = 180°
=> 5x + 20° = 180°
=> 5x = 180° – 20°

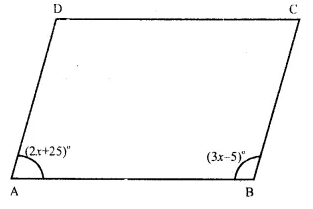
=> 5x = 160° => x = \(\frac { { 160 }^{ o } }{ 5 } \) = 32°
∴x = 32°
Now ∠A = 2x + 25° = 2 x 32° + 25°
= 64° + 25° = 89°
∠B = 3x – 5 = 3 x 32° – 5°
= 96° – 5° = 91°
∠ C = ∠ A (∴ opposite angles of ||gm)
= 89°
Similarly ∠B = ∠D
∠D = 91°
Hence ∠ A = 89°, ∠ B = 91°, ∠ C = 89°, ∠D = 91° Ans.

Question 6.
Solution:
Let ∠A and ∠B of a ||gm ABCD are adjacent angles.
∠A + ∠B = 180°
Let ∠B = x

Then ∠ A = \(\frac { 4 }{ 5 } \) x
∴ x + \(\frac { 4 }{ 5 } \) x = 180°
\(\frac { 9 }{ 5 } \) x = 180°
=>\(\frac { { 180 }^{ o }\quad X\quad 5 }{ 9 } \) = 100°
∴ ∠A = \(\frac { 4 }{ 5 } \) x 100° = 80°
and ∠B = 100°
But ∠ C = ∠ A and ∠ D = ∠ B
(opposite angles of a || gm)
∴∠C = 80°, and ∠D = 100°
Hence ∠A = 80°, ∠B = 100°, ∠C = 80° and ∠ D = 100° Ans.

Question 7.
Solution:
Let the smallest angle ∠ A and the other angle ∠ B
Let ∠ A = x
Then ∠ B = 2x – 30°
But ∠ A + ∠ B = 180° (co-interior angles)
∴x + 2x – 30° = 180°
=> 3x = 180° + 30° = 210°
=> x = \(\frac { { 210 }^{ o } }{ 3 } \) = 70°
∴ ∠ A = 70°

and ∠ B = 2x – 30° = 2 x 70° – 30°
= 140° – 30° = 110°
But ∠C = ∠ A and ∠D = ∠B
(opposite angles of a ||gm)
∠C = 70° and ∠D = 110°
Hence ∠A = 70°, ∠B = 110°, ∠C = 70° and ∠D = 110° Ans.

Question 8.
Solution:
In ||gm ABCD,
AB = 9.5 cm and perimeter = 30 cm
=> AB + BC + CD + DA = 30cm
=> AB + BC + AB + BC = 30 cm
( ∴ AB = CD and BC – DA opposite sides)

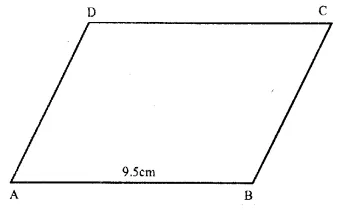
=> 2(AB + BC) = 30cm
=> AB + BC = 15cm
=> 9 5cm + BC = 15cm
∴BC = 15cm – 9.5cm = 5.5cm
Hence AB = 9.5cm, BC = 5.5cm,
CD = 9.5cm and DA = 5.5cm Ans.

Question 9.
Solution:
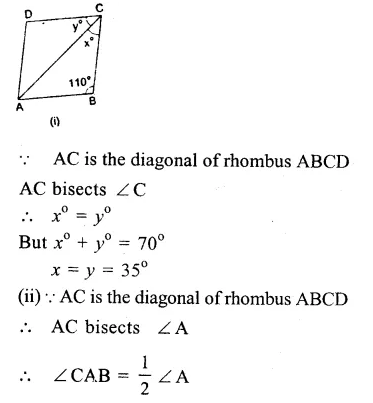
ABCD is a rhombus
AB = BC = CD = DA
(i)∴ AB || DC
∴ ∠ B + ∠ C = 180° (co-interior angles)
=> 110° + ∠C = 180°
=> ∠C = 180° – 110° = 70°

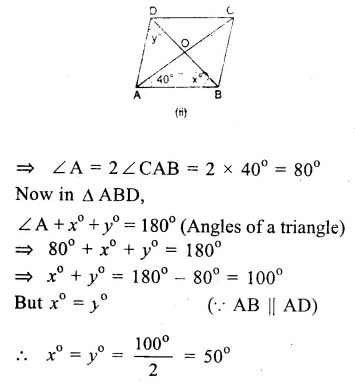
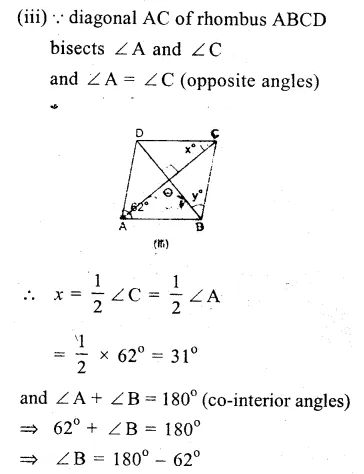
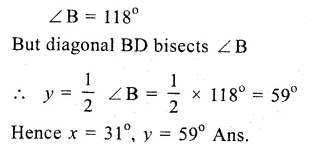
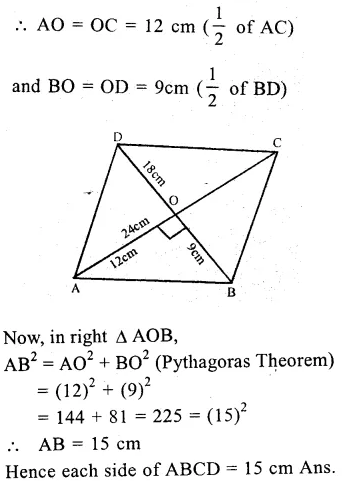
Question 10.
Solution:
In a rhombus,
Diagonals bisect each other at right angles
∴ AC and BC bisect each other at O at right angles.
But AC = 24 cm and BD = 18 cm

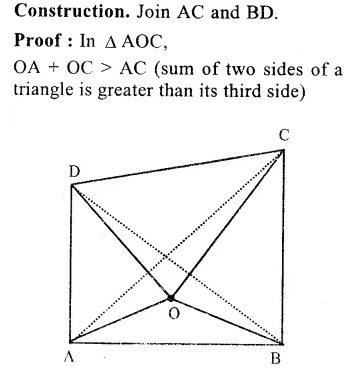
Question 11.
Solution:
Let ABCD he the rhombus whose diagonal are AC and BD which bisect each other at right angles at O.

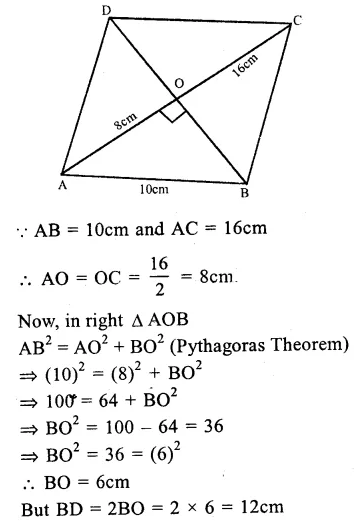
Question 12.
Solution:
ABCD is a rectangle whose diagonals AC and BD bisect each other at O.

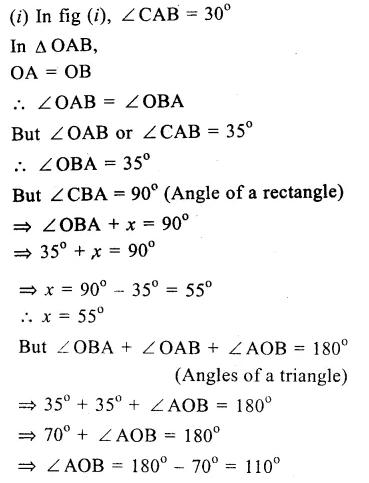
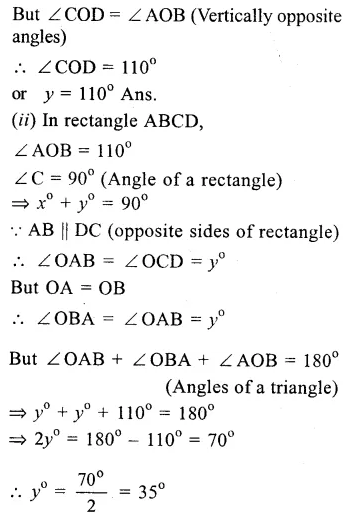
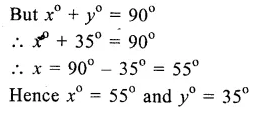
Question 13.
Solution:
ABCD is a square. A line CX cuts AB at X and diagonal BD at O such that
∠ COD = 80° and ∠ OXA = x°
∴∠ BOX = ∠ COD
(vertically opposite angles)
∴∠BOX = 80°
∴Diagonal BD bisects ∠ B and ∠ D
∴ ∠ABO or ∠ABD = ∠ ADO or ∠ ADB
∴ ∠OBA or ∠OBX = 45°
Now in ∆ OBX,
Ext. ∠ OXA = ∠ BOX + ∠ OBX
=>x° = 80° + 45° = 125° Ans.

Question 14.
Solution:
Given : In ||gm ABCD, AC is joined. AL ⊥ BD and CM ⊥ BD
To prove :
(i) ∆ ALD ≅ ∆ CMB
(ii) AL = CM
Proof : In ∆ ALD and ∆ BMC
AD = BC (opposite sides of ||gm)
∠L = ∠M (each 90°)
∠ ADL = ∠ CBM (Alternate angles)
∴ ∆ ALD ≅ ∆ BMC. (AAS axiom)
∴ or A ALD ≅ A CMB.
AL = CM (c.p.c.t.) Hence proved.

Question 15.
Solution:
Given : In ∆ ABCD, bisectors of ∠A and ∠B meet each other at P.
To prove : ∠APB = 90°
Proof : AD || BC
∠A + ∠B = .180° (co-interior angles)
PA and PB are the bisectors of ∠ A and ∠B

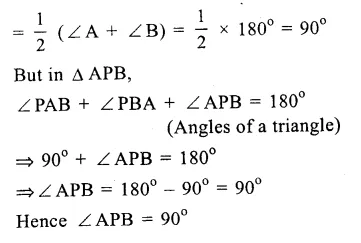
Question 16.
Solution:
In ||gm ABCD,
P and Q are the points on AD and BC respectively such that AP = \(\frac { 1 }{ 3 } \) AD and CQ = \(\frac { 1 }{ 3 } \) BC

Question 17.
Solution:
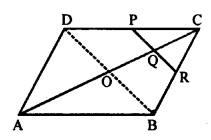
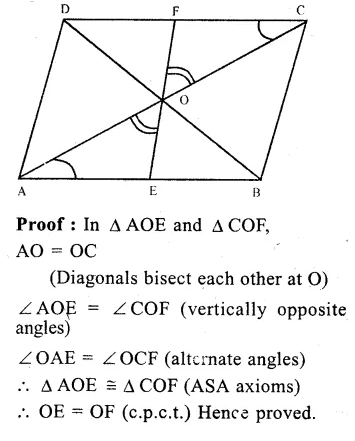
Given : In ||gm ABCD, diagonals AC and BD bisect each other at O.
A line segment EOF is drawn, which meet AB at E and DC at F.
To -prove : OE = OF

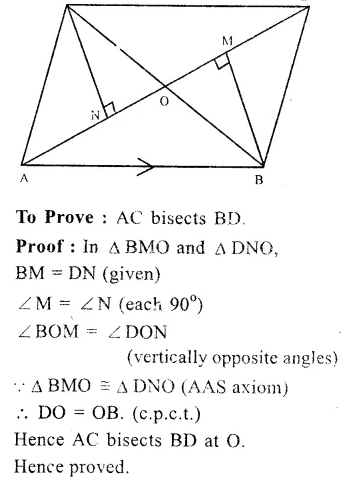
Question 18.
Solution:
Given : ABCD is a ||gm.
AB is produced to E. Such that AB = BE
DE is joined which intersects BC in O.
To prove : ED bisects BC i.e. BO = OC

Question 19.
Solution:
Given : In ||gm ABCD, E is the midpoint BC
DE is joined and produced to meet AB on producing at F.

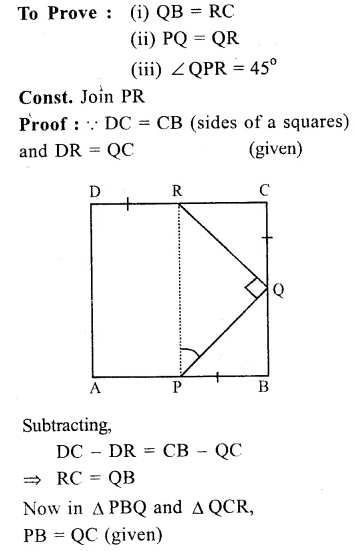
Question 20.
Solution:
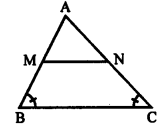
Given : ∆ ABC and lines are drawn through A, B and C parallel to respectively BC, CA and AB forming ∆ PQR.
To prove : BC = \(\frac { 1 }{ 2 } \) QR

Question 21.
Solution:
Given : In ∆ ABC, parallel lines are drawn through A, B and C respectively to the sides BC, CA and AB intersecting each other at P, Q and R.

Hope given RS Aggarwal Class 9 Solutions Chapter 9 Quadrilaterals and Parallelograms Ex 9B are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 9 Solutions Chapter 9 Quadrilaterals and Parallelograms Ex 9A

These Solutions are part of RS Aggarwal Solutions Class 9. Here we have given RS Aggarwal Class 9 Solutions Chapter 9 Quadrilaterals and Parallelograms Ex 9A.

Other Exercises

• RS Aggarwal Solutions Class 9 Chapter 9 Quadrilaterals and Parallelograms Ex 9A
• RS Aggarwal Solutions Class 9 Chapter 9 Quadrilaterals and Parallelograms Ex 9B
• RS Aggarwal Solutions Class 9 Chapter 9 Quadrilaterals and Parallelograms Ex 9C

Question 1.
Solution:
We know that sum of angles of a quadrilateral is 360°
Now, sum of three angles = 56° + 115° + 84° = 255°
Fourth angle = 360° – 255° = 105° Ans.

Question 2.
Solution:
Sum of angles of a quadrilateral = 360°
Their ratio = 2 : 4 : 5 : 7
Let first angle = 2x
then second angle = 4x
third angle = 5x
and fourth angle = 7x
∴ 2x + 4x + 5x + 7x = 360°
=> 18x = 360°
=> x = \(\frac { { 360 }^{ o } }{ 18 } \) = 20°
Hence, first angle = 2x = 2 x 20° = 40°
Second angle = 4x = 4 x 20° = 80°
Third angle = 5x = 5 x 20° = 100°
and fourth angle = 7x = 7 x 20° = 140°Ans.

Question 3.
Solution:
In the trapezium ABCD
DC || AB
∴ ∠ A + ∠ D = 180° (Co-intericr angles)
∴ 55°+ ∠D = 180°
∠D = 180° – 55°
∴ ∠D = 125°
Similarly, ∠B + ∠C = 180°
(Co-interior angles)
=> 70° + ∠C = 180°
=> ∠C = 180° – 70°
∠C = 110°
Hence ∠C = 110° and ∠D = 125° Ans.

Question 4.
Solution:
Given : In the figure, ABCD is a square and ∆ EDC is an equilateral triangles on DC. AE and BE are joined.
To Prove : (i) AE = BE
(ii) ∠DAE = 15°

Question 5.
Solution:
Given : In the figure,
BM ⊥ AC, DN ⊥ AC.
BM = DN

Question 6.
Solution:
Given : In quadrilateral ABCD,
AB = AD and BC = DC
AC is joined.
To Prove : (i) AC bisects ∠ A and ∠ C
(ii) BE = DE
(iii) ∠ABC = ∠ADC
Const. Join BD.
Proof : (i) In ∆ ABC and ∆ ADB

Question 7.
Solution:
Given : In square ABCD,
∠ PQR = 90°
PB = QC = DR

Question 8.
Solution:
Given : In quadrilateral ABCD, O is any point inside it. OA, OB, OC and OD are joined.
To Prove : OA + OB + OC + OD > AC + BD

Question 9.
Solution:
Given : In quadrilateral ABCD, AC is its one diagonal.

Question 10.
Solution:
Given : A quadrilateral ABCD
To Prove : ∠A + ∠B + ∠C + ∠D = 360°
Const. Join AC.

Hope given RS Aggarwal Class 9 Solutions Chapter 9 Quadrilaterals and Parallelograms Ex 9A are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 9 Solutions Chapter 8 Linear Equations in Two Variables Ex 8A

These Solutions are part of RS Aggarwal Solutions Class 9. Here we have given RS Aggarwal Class 9 Solutions Chapter 8 Linear Equations in Two Variables Ex 8A.

Question 1.
Solution:
(i) x = 5 is the line AB parallel to the y-axis at a distance of 5 units.
(ii) y = – 2 is the line CD parallel to x-axis at a distance of – 2 units.
(iii) x + 6 = 0 => x = – 6 is the line EF parallel to y-axis at a distance of – 6 units.
(iv) x + 7 = 0 => x = – 7 is the line PQ parallel to y-axis at a distance of – 7 units.
(v) y = 0 is the equation of x-axis. The graph of y = 0 is the line X’OX
(vi) x = 0 is the equation of y-axis.The graph of x = 0 is the line YOY’
Ans.

Question 2.
Solution:
In the given equation.

y = 3x
Put x = 1, then y = 3 x 1 = 3
Put x = 2, then y = 3 x 2 = 6
Put x = – 1, then y = 3 ( – 1) = – 3
Now, plot the points (1, 3), (2, 6) and ( – 1, – 3) as given the following table

and join them to form a line of the given equation.
Now from x = – 2,
draw a line parallel to y-axis at a distance of x = – 2, meeting the given line at P. From P, draw, a line parallel to x-axis joining y-axis at M, which is y = – 6 Hence, y = – 6 Ans.

Question 3.
Solution:
In the given equation x + 2y – 3 = 0
=> 2y = 3 – x
y = \(\frac { 3-x }{ 2 } \)
put x = 1,then

Question 4.
Solution:
(i) In the equation y = x
When x = 1, then y = 1
when x = 2, then y = 2
and when x = 3, then y = 3

Question 5.
Solution:
In the given equation
2x – 3y = 5

Question 6.
Solution:
In the given equation
2x + y = 6
=> y = 6 – 2x
Put x = 1, then y – 6 – 2 x 1 = 6 – 2 = 4
Put x = 2, then y = 6 – 2 x 2 = 6 – 4 = 2
Put x = 3, then y = 6 – 2 x 3 = 6 – 6 = 0

Question 7.
Solution:
In the given equation
3x + 2y = 6

Hope given RS Aggarwal Class 9 Solutions Chapter 8 Linear Equations in Two Variables Ex 8A are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 10 Solutions Chapter 4 Triangles Ex 4A

These Solutions are part of RS Aggarwal Solutions Class 10. Here we have given RS Aggarwal Solutions Class 10 Chapter 4 Triangles Ex 4A.

Other Exercises

• RS Aggarwal Solutions Class 10 Chapter 4 Triangles Ex 4A
• RS Aggarwal Solutions Class 10 Chapter 4 Triangles Ex 4B
• RS Aggarwal Solutions Class 10 Chapter 4 Triangles Ex 4C
• RS Aggarwal Solutions Class 10 Chapter 4 Triangles Ex 4D
• RS Aggarwal Solutions Class 10 Chapter 4 Triangles Ex 4E
• RS Aggarwal Solutions Class 10 Chapter 4 Triangles MCQS
• RS Aggarwal Solutions Class 10 Chapter 4 Triangles Test Yourself

Question 1.
Solution:
In ∆ABC, points D and E are on the sides AB and AC respectively such that DE || BC.



⇒ 7x = 28 ⇒ x = 4

Question 2.
Solution:
D and E are the points on the sides AB and AC of ∆ABC respectively and DE || BC,


By cross multiplication,
⇒ (7x – 4) (3x) = (5x – 2) (3x + 4)
⇒ 21x² – 12x = 15x² + 20x – 6x – 8
⇒ 21x² – 12x – 15x² – 20x + 6x = -8
⇒ 6x² – 26x + 8 = 0
⇒ 3x² – 13x + 4 = 0
⇒ 3x² – 12x – x + 4 = 0
⇒ 3x (x – 4) – 1 (x – 4) = 0
⇒ (x – 4) (3x – 1) = 0
Either x – 4 = 0, then x = 4
or 3x – 1 = 0 then 3x = 1 ⇒ x = \(\frac { 1 }{ 3 }\) which is not possible
x = 4

Question 3.
Solution:
D and E are the points on the sides AB and AC of ∆ABC
(i) AD = 5.7 cm, DB = 9.5 cm, AE = 4.8 cm and EC = 8 cm

Question 4.
Solution:
In ∆ABC, AD is the bisector of ∠A

Question 5.
Solution:
Given : M is a point on the side BC of a parallelogram ABCD.
DM when produced meets AB produced at N.

Question 6.
Solution:
Given : In trapezium AB || DC.
M and N are the mid points of sides AD and BC respectively.
MN is joined.
To prove : MN || AB or DC.
Construction: Produce AD and BC to meet at P.

Question 7.
Solution:
ABCD is a trapezium and its diagonals AC and BD intersect each other at O.

Question 8.
Solution:
Given : In ∆ABC, M and N are points on the sides AB and AC respectively such that
BM = CN and if ∠B = ∠C.

Question 9.
Solution:
Given : ∆ABC and ∆DBC are on the same side of BC.
P is any point on BC.
PQ || AB and PR || BD are drawn, which meet AC at Q and CD at R.
AD is joined.
To prove : QR || AD.
Proof:
In ∆ABC, PQ||AB


Hence proved.

Question 10.
Solution:
Given : In the given figure, D is the mid point of BC. AD is joined. O is any point on AD. BO and CO are produced to meet AC at F and AB at E respectively. AD is produced to X such that D is the mid point of OX.
To prove: AO : AX = AF : AB and EF || BC
Construction. Join BX and CX.

D is the midpoint of BC.
Proof: BD = DC and OD = DX. (given)
OBXC is a parallelogram. (Diagonals of a ||gm bisect each other)

Question 11.
Solution:
Given : In ||gm, ABCD, P is mid point of DC and Q is the mid point of AC. Such that
CQ = \(\frac { 1 }{ 4 }\) AC.
PQ is produced to meet BC at R.
To prove : R is the mid point of BC.
Construction : Join BD which intersects AC at O.

Proof: Diagonals of a parallelogram bisect each other
CO = \(\frac { 1 }{ 2 }\) AC.
But CQ = \(\frac { 1 }{ 2 }\) CO (given)
Q is the mid point of CO.
PQ || DO
⇒ PR || DB and P is mid point of CD
R is the midpoint BC.
Hence proved.

Question 12.
Solution:
Given : In ∆ABC, AB = AC
D and E are the points on AB and AC such that
AD = AE
To prove : BCED is a cyclic quadrilateral.
Proof: In ∆ABC,
AB = AC,
D and E are the mid points of AB and AC respectively.

But these are opposite angles of quad. BCED
BCED is a cyclic quadrilateral
Hence, B, C, E and D are concyclic.

Question 13.
Solution:
Given : In ∆ABC, BD is the bisector of AB which meets AC at D.
A line PQ || AC which meets AB, BC, BD at P, Q, R respectively.
To prove : PR x BQ = QR x BP
Proof: In ∆ABC, PQ || AC
and BD is the bisector of ∠B

Hope given RS Aggarwal Solutions Class 10 Chapter 4 Triangles Ex 4A are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.