RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials Ex 6.3

RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials Ex 6.3

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials Ex 6.3

Other Exercises

• RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials Ex 6.1
• RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials Ex 6.2
• RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials Ex 6.3
• RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials Ex 6.4
• RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials Ex 6.5
• RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials VSAQS
• RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials MCQS

In each of the following, using the remainder Theorem, find the remainder when f(x) is divided by g(x) and verify the result by actual division (1 – 8) :

Question 1.
f(x) = x³ + 4x² – 3x + 10, g(x) = x + 4
Solution:

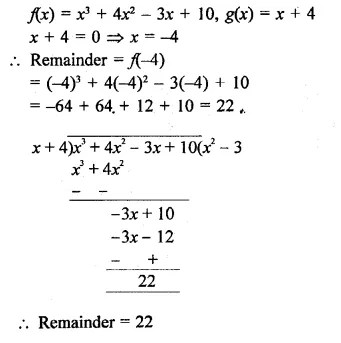
Question 2.
f(x) – 4x⁴ – 3x³ – 2x² + x – 7, g(x) = x – 1
Solution:

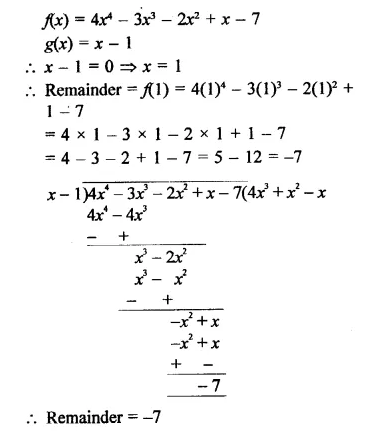
Question 3.
f(x) = 2x⁴ – 6X³ + 2x² – x + 2, ,g(x) = x + 2
Solution:

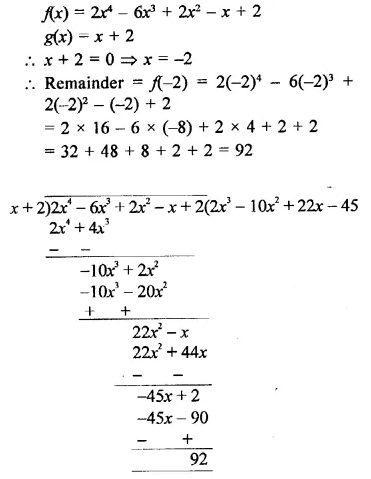
Question 4.
f(x) = 4x³ – 12x² + 14x – 3, g(x) = 2x – 1
Solution:

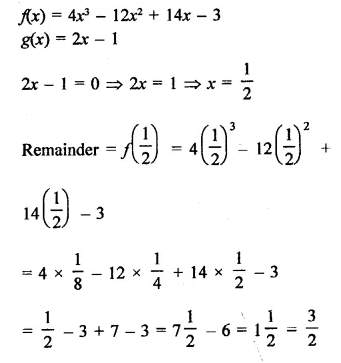
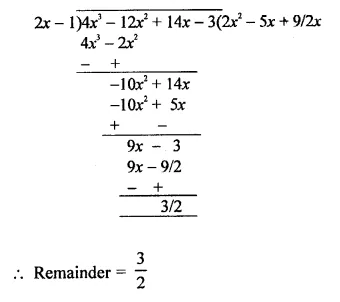
Question 5.
f(x) = x³ – 6x² + 2x – 4, g(x) = 1 – 2x
Solution:

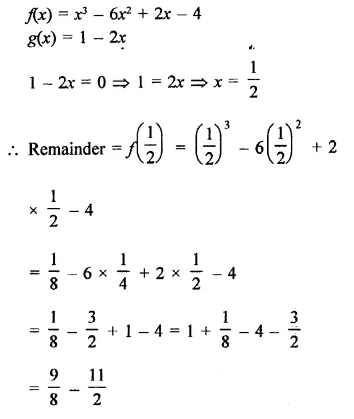
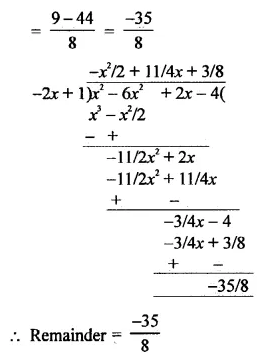
Question 6.
f(x) = x⁴ – 3x² + 4, g(x) = x – 2
Solution:

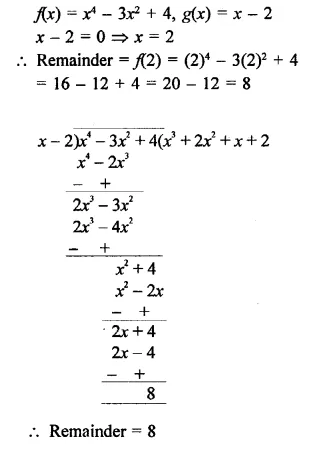
Question 7.

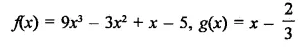
Solution:

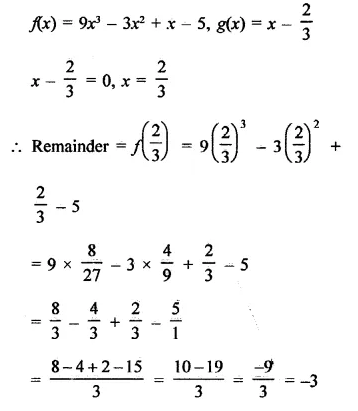
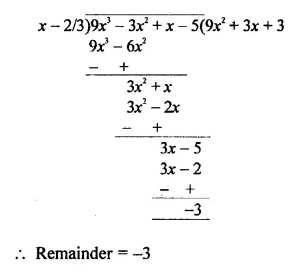
Question 8.

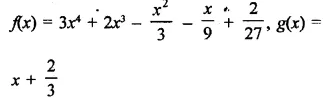
Solution:

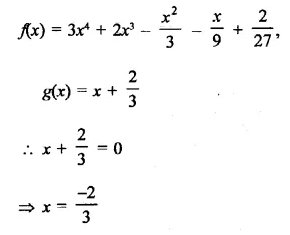
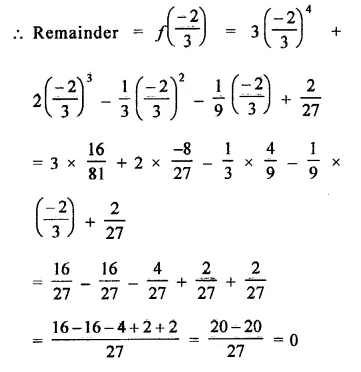
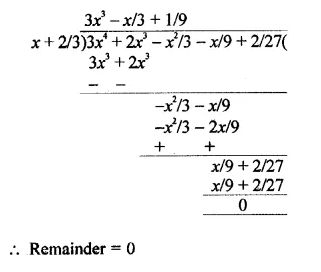
Question 9.
If the polynomials 2x³ + ax² + 3x – 5 and x³ + x² – 4x + a leave the same remainder when divided by x – 2, find the value of a.
Solution:
Let f(x) = 2x³ + ax² + 3x – 5
g(x) = x³+x²-4x + a
q(x) = x –  2 ⇒ x-2 = 0  ⇒x = 2
∴ Remainder =f(2) = 2(2)³ + a(2)² + 3 x 2-5
= 2 x 8 4-a x 4 + 3 x 2-5
= 16 + 4a + 6 – 5
= 4a +17
and g(2) = (2)³ + (2)² -4×2 + a
= 8 + 4 – 8 + a = a + 4
∵  In both cases, remainder are same
∴  4a + 17 = a + 4
⇒  4a – a = 4 – 17 ⇒  3a = -13
⇒ a = \(\frac { -13 }{ 3 }\)
Hence a = \(\frac { -13 }{ 3 }\)

Question 10.
If the polynomials ax³ + 3x² – 13 and 2x³ – 5x + a, when divided by (x – 2), leave the same remainders, find the value of a.
Solution:
Let p(x) = ax³ + 3x² – 13
q(x) = 2x³ –5x + a
and divisor g(x) = x – 2
x-2 = 0
⇒ x = 2
∴ Remainder = p(2) = a(2)³ + 3(2)² – 13
= 8a + 12 – 13 = 8a – 1
and q( 2) = 2(2)³ – 5×2 + a=16-10 + a
= 6 + a
∵  In each case remainder is same
∴ 8a – 1 = 6 + a
8a – a = 6 + 1
⇒  7a = 7
⇒ a = \(\frac { 7 }{ 7 }\)= 1
∴ a = 1

Question 11.
Find the remainder when x³ + 3x² + 3x + 1 is divided by

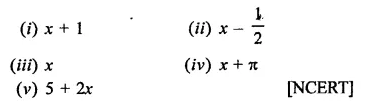
Solution:

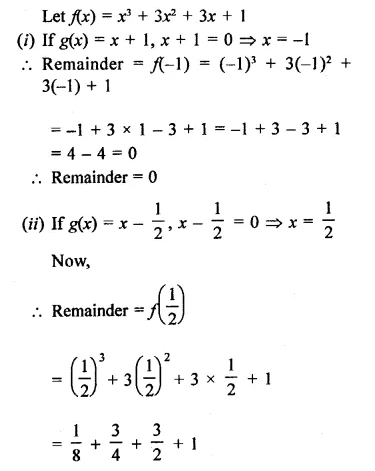
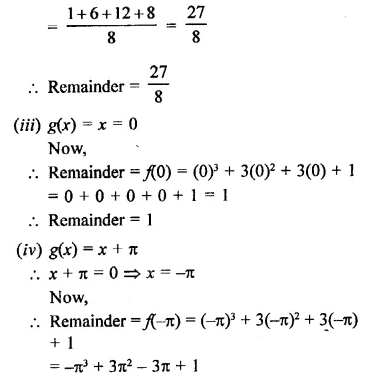
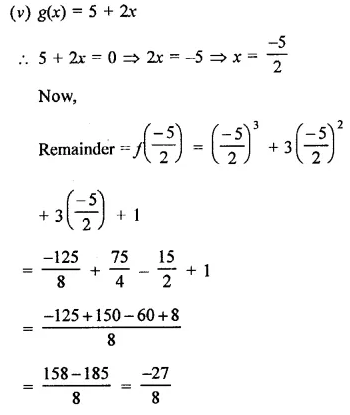
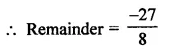
Question 12.
The polynomials ax³ + 3a-² – 3 and 2x³ – 5x + a when divided by (x – 4) leave the remainders R₁ and R₂, respectively. Find the values of a in each case of the following cases, if
(i) R₁ = R₂
(ii) R₁ + R₂ = 0
(iii) 2R₁ – R₂ = 0.
Solution:

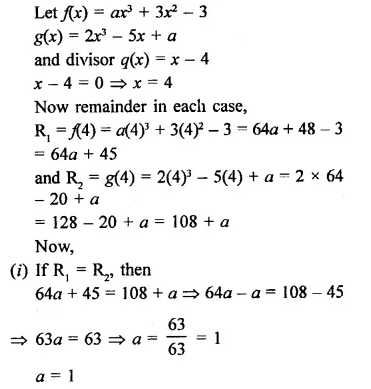
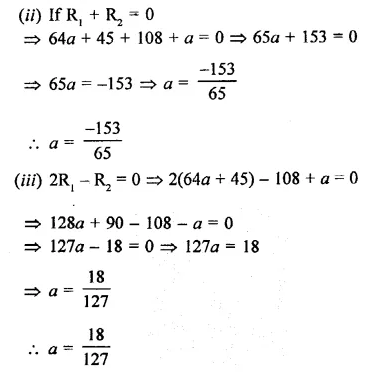
Hope given RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials Ex 6.3 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.