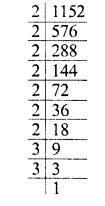
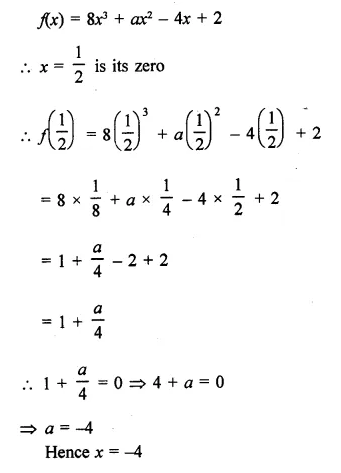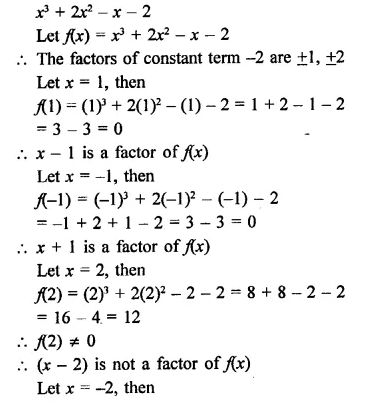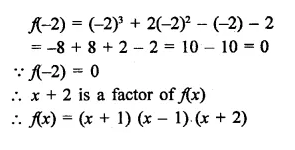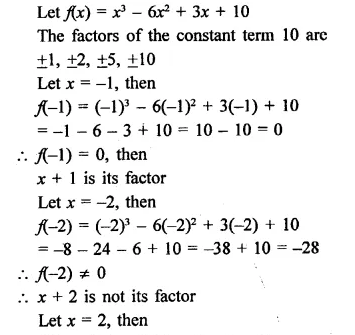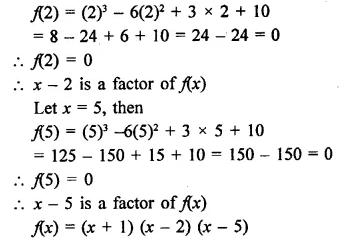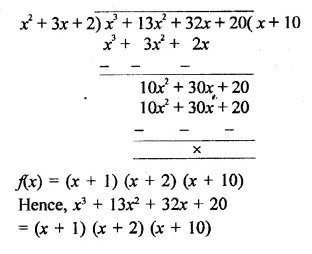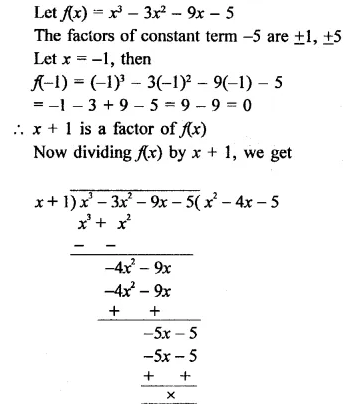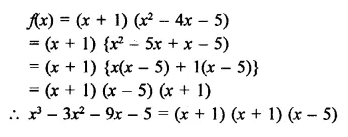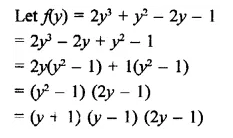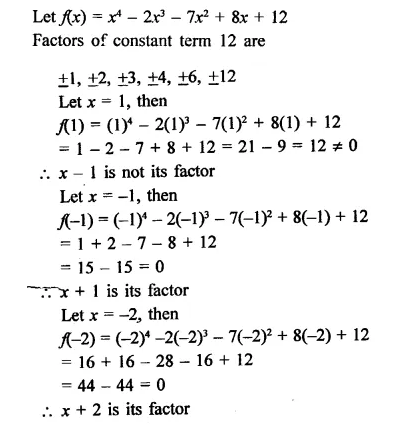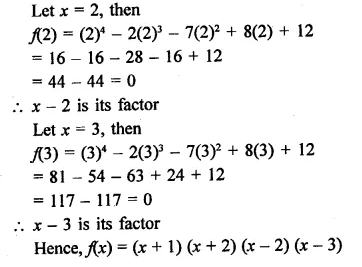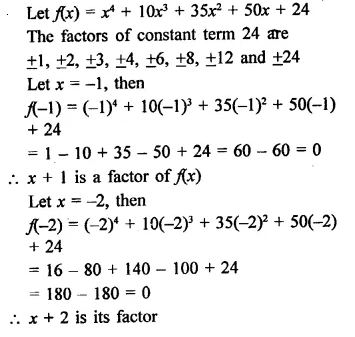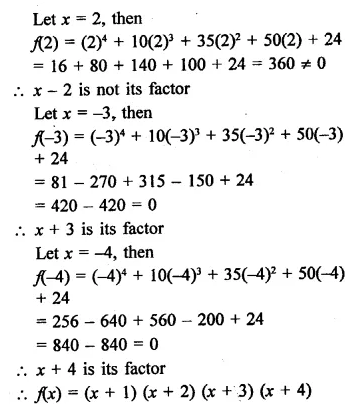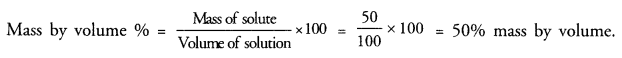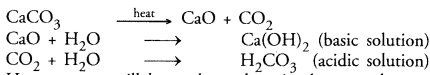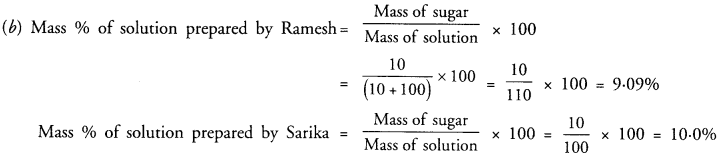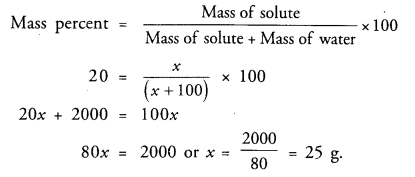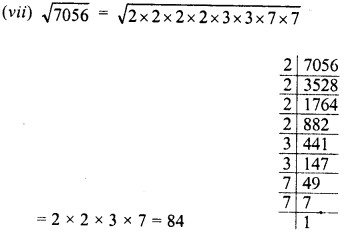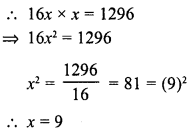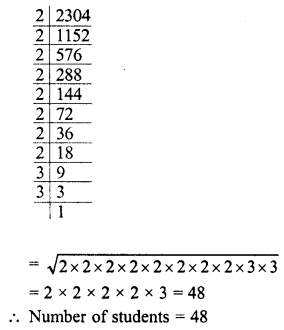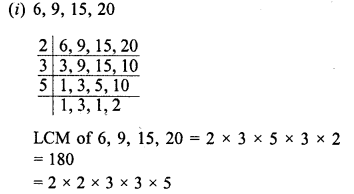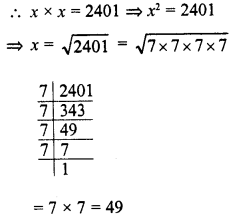Prasanna

RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials VSAQS

by

RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials VSAQS

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials VSAQS

Other Exercises

Question 1.
Define zero or root of a polynomial.
Solution:
A real number a is a zero or root of a polynomial f(x) if f(α) = 0

Question 2.
If x = \(\frac { 1 }{ 2 }\) is a zero of the polynomial f(x) =  8x3 + ax2 – 4x + 2, find the value of a.
Solution:
RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials VSAQS Q2.1

Question 3.
Write the remainder when the polynomial f(x) = x3+x2-3x + 2is divided by x + 1.
Solution:
f(x) = x3+x2-3x + 2
Let x + 1 = 0, then x = -1
∴ Remainder =(-1)
Now,f(-1) = (-1)3 + (-1)2 – 3(-1) + 2
= -1 + 1+ 3 + 2 = 5
∴ Remainder = 5

Question 4.
Find the remainder when x3 + 4x2 + 4x – 3 is divided by x.
Solution:
f(x) = x3 + 4x2 + 4x – 3
Dividing f(x) by x, we get
Let x = 0, then
f(x) = 0 + 0 + 0 – 3 = -3
∴  Remainder = -3

Question 5.
If x + 1 is a factor of x3 + a, then write the value of a.
Solution:
Let f(x) = x3 + a
∴ x + 1 is a factor of fx)
Let x + 1 = 0
⇒ x = -1
∴ f(-1) = x3 + a
= (-1)3 + a = -1 + a
∴  x + 1 is a factor
∴  Remainder = 0
∴  -1 + a = 0 ⇒  a = 1
Hence a = 1

Question 6.
If f(x) = x4-2x3 + 3x2 – ax – b when divided by x – 1, the remainder is 6, then find the value of a + b.
Solution:
f(x) = x4 – 2x3 + 3x2 – ax – b
Dividing f(x) by x – 1, the remainder = 6
Now let x – 1 = 0, then x = 1
∴  f(1) = (1)4 – 2(1)3 + 3(1)2 -ax 1-b
= 1 -2 + 3-a-b = 2-a-b
∴ Remainder = 6
∴ 2 – a – b = 6  ⇒ a + b = 2 – 6 = -4
Hence a + b = -4

Hope given RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials VSAQS are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 10 Solutions Chapter 4 Triangles Ex 4B

by

RS Aggarwal Class 10 Solutions Chapter 4 Triangles Ex 4B

These Solutions are part of RS Aggarwal Solutions Class 10. Here we have given RS Aggarwal Solutions Class 10 Chapter 4 Triangles Ex 4B.

Other Exercises

Question 1.
Solution:
We know that two triangles are similarity of their corresponding angles are equal and corresponding sides are proportional.
(i) In ∆ABC and ∆PQR
∠A = ∠Q = 50°
∠B = ∠P = 60° and ∠C = ∠R = 70°
∆ABC ~ ∆QPR (AAA axiom)
(ii) In ∆ABC and ∆DEF
In ∆ABC,
AB = 3 cm, BC = 4.5
and in ∆DEF
DF = 6 cm, DE = 9 cm
∆ABC is not similar to ∆DEF
As in ∆ABC, ∠A is not included of two sides AB and BC.
(iii) In ∆ABC and ∆PQR
In ∆ABC,
AC = 8 cm BC = 6 cm
Included ∠C = 80°
In ∆PQR,
PQ = 4.5 cm, QR = 6 cm
and included ∠Q = 80°
RS Aggarwal Class 10 Solutions Chapter 4 Triangles Ex 4B 1
(v) In ∆ABC,
∠A = 80°, ∠C = 70°
and third angle
∠B = 180° – (80° + 70°)
⇒ ∠B = 180° – 150° = 30°
In ∆MNR,
∠M = 80°, ∠N = 30°, and ∠R = [180° – (80° + 30°)]
∠R = 180° – 110° = 70°
Now, in ∆ABC
∠A = ∠M – 80°, ∠B = ∠N = 30°
and ∠C = ∠R = 70°
∆ABC ~ ∆MNR (AAA or AA axiom)

Question 2.
Solution:
In the given figure, ∆ODC ~ ∆OBA and ∠BOC =115°, ∠CDO = 70°
RS Aggarwal Class 10 Solutions Chapter 4 Triangles Ex 4B 2
To find :
(i) ∠DOC
(ii) ∠DCO
(iii) ∠OAB
(iv) ∠OBA
∆ODC ~ ∆OBA
∠D = ∠B = 70°
∠C = ∠A
∠COD = ∠AOB
(i) But ∠DOC + ∠BOC = 180° (Linear pair)
⇒ ∠DOC + 115°= 180°
⇒ ∠DOC = 180° – 115° = 65°
(ii) ∠DOC + ∠CDO + ∠DCO = 180° (Angles of a triangle)
⇒ 65° + 70° + ∠DCO = 180°
⇒ 135° + ∠DCO = 180°
⇒ ∠DCO = 180° – 135°
∠DCO = 45°
(iii) ∠AOB = ∠DOC = 65° (vertically opposite angles)
∠OAB = ∠DCO = 45° (∆ODC ~ ∆OBA)
(iv) ∠OBA = ∠CDO = 70° (∆ODC ~ ∆OBA)

Question 3.
Solution:
In the given figure, ∆OAB ~ ∆OCD
AB = 8 cm, BO = 6.4 cm OC = 3.5 cm, CD = 5 cm
RS Aggarwal Class 10 Solutions Chapter 4 Triangles Ex 4B 3
RS Aggarwal Class 10 Solutions Chapter 4 Triangles Ex 4B 4

Question 4.
Solution:
Given : In the given figure,
∠ADE = ∠B
To prove:
(i) ∆ADE ~ ∆ABC
(ii) If AD = 3.8 cm, AE = 3.6 cm, BE = 2.1 cm and BC = 4.2 cm, find DE
Proof: (i) In ∆ADE and ∆ABC
∠ADE = ∠B (given)
∠A = ∠A (common)
∆ADE ~ ∆ABC (AA axiom)
RS Aggarwal Class 10 Solutions Chapter 4 Triangles Ex 4B 5

Question 5.
Solution:
∆ABC ~ ∆PQR,
PQ = 12 cm
To find AB.
Perimeter of ∆ABC = AB + BC + CA = 32 cm
Perimeter of ∆PQR = PQ + QR + RP = 24 cm
Now,
∆ABC ~ ∆PQR
RS Aggarwal Class 10 Solutions Chapter 4 Triangles Ex 4B 6

Question 6.
Solution:
∆ABC ~ ∆DEF
BC = 9.1 cm, EF = 6.5 cm
Perimeter of ∆DEF = 25 cm
RS Aggarwal Class 10 Solutions Chapter 4 Triangles Ex 4B 7
RS Aggarwal Class 10 Solutions Chapter 4 Triangles Ex 4B 8

Question 7.
Solution:
Given : In the given figure,
∠CAB = 90° and AD ⊥ BC
To prove : ∆BDA ~ ∆BAC
If AC = 75 cm, AB = 1 m or 100 cm,
BC = 1.25 m or 125 cm
Find AD.
∆BDA ~ ∆BAC (corresponding sides and proportional)
RS Aggarwal Class 10 Solutions Chapter 4 Triangles Ex 4B 9

Question 8.
Solution:
In the given figure,
∠ABC = 90°, BD ⊥ AC.
AB = 5.7 cm, BD = 3.8 cm, CD = 5.4 cm
To find BC,
In ∆ABC and ∆BDC,
∠ABC = ∠BDC (each 90°)
∠BCA = ∠BCD (common)
∆ABC ~ ∆BDC (AA axiom)
Corresponding sides are proportional
RS Aggarwal Class 10 Solutions Chapter 4 Triangles Ex 4B 10

Question 9.
Solution:
In the given figure, ”
∠ABC = 90°, BD ⊥ AC
BD = 8 cm, AD = 4cm
To find CD,
Let CD = x
Now in ∆DBC and ∆BDA
∠BDC = ∠BDA (each 90°)
∠C = ∠ABD
∆DBC ~ ∆BDA
Sides are proportional
RS Aggarwal Class 10 Solutions Chapter 4 Triangles Ex 4B 11

Question 10.
Solution:
In ∆ABC, P and Q are points on the sides AB and AC respectively such that
AP = 2 cm, PB = 4 cm, AQ = 3 cm and QC = 6 cm.
To prove : BC = 3 PQ
RS Aggarwal Class 10 Solutions Chapter 4 Triangles Ex 4B 12
BC = 3 PQ
Hence proved.

Question 11.
Solution:
Given: ABCD is a parallelogram.
E is a point on BC and diagonal BD intersects AE at F.
RS Aggarwal Class 10 Solutions Chapter 4 Triangles Ex 4B 13
To prove : AF x FB = EF x FD
Proof: In ∆AFD and ∆BFE
∠AFD = ∠BFE (vertically opposite angles)
∠ADF = ∠FBE (alternate angles)
∆AFD ~ ∆BFE (AA axiom)
\(\frac { AF }{ EF }\) = \(\frac { FD }{ FB }\)
By cross multiplication,
⇒ AF x FB = EF x FD
Hence proved.

Question 12.
Solution:
Given : In the given figure,
DB ⊥ BC, DE ⊥ AB and AC ⊥ BC
RS Aggarwal Class 10 Solutions Chapter 4 Triangles Ex 4B 14

Question 13.
Solution:
In ∆ABC and ∆DEF
AC is stick and BC is its shadow.
DF is the tower and EF is its shadow
AC = 7.5 m, BC = 5 m EF = 24 m,
let DF = x m
RS Aggarwal Class 10 Solutions Chapter 4 Triangles Ex 4B 15
RS Aggarwal Class 10 Solutions Chapter 4 Triangles Ex 4B 16

Question 14.
Solution:
Given : In isosceles ∆ABC,
CA = CB, base AB and BA are produced in P and Q such that
AP x BQ = AC²
To prove : ∆ACP ~ ∆BCQ
Proof: In ∆ABC,
CA = CB
∠CAB = ∠CBA (Angles opposite to equal sides)
⇒ 180° – ∠CAB = 180° – ∠CBA (Subtracting each from 180°)
⇒ ∠CAP = ∠CBQ
AP x BQ = AC² (given)
RS Aggarwal Class 10 Solutions Chapter 4 Triangles Ex 4B 17

Question 15.
Solution:
Given : In the given figure, ∠1 = ∠2
RS Aggarwal Class 10 Solutions Chapter 4 Triangles Ex 4B 18

Question 16.
Solution:
Given : In quadrilateral ABCD,
AD = BC
P, Q, R and S are midpoints of AB, AC, CD and BD respectively.
RS Aggarwal Class 10 Solutions Chapter 4 Triangles Ex 4B 19
To proof : PQRS is a rhombus.
Proof: In ∆ABC,
P and Q are the midpoints of sides AB and AC respectively.
PQ || BC ……(i)
RS Aggarwal Class 10 Solutions Chapter 4 Triangles Ex 4B 20

Question 17.
Solution:
In the given circle, two chords AB and CD intersect each other at P inside the circle.
To prove :
(a) ∆PAC ~ ∆PDB
(b) PA . PB = PC . PD
Proof:
(a) In ∆PAC and ∆PDB
∠APC = ∠BPD (Vertically opposite angles)
∠A = ∠D (Angles in the same segment)
∆PAC ~ ∆PDB (AA axiom)
\(\frac { PA }{ PD }\) = \(\frac { PC }{ PB }\)
⇒ PA x PB = PC x PD
Hence proved.

Question 18.
Solution:
In a circle, two chords AB and CD intersect each other at the point P outside the circle.
AC and BD are joined.
RS Aggarwal Class 10 Solutions Chapter 4 Triangles Ex 4B 21
To prove :
(a) ∆PAC ~ ∆PDB
(b) PA . PB = PC . PD
Proof: In the circle, quadrilateral ABDC is a cyclic.
Ext. ∠PAC = ∠D
Now, in ∆PDB and ∆PAC
∠P = ∠P (common)
∠PAC = ∠D (proved)
∆PDB ~ ∆PAC (AA axiom)
or ∆PAC ~ ∆PBD
\(\frac { PA }{ PD }\) = \(\frac { PC }{ PB }\)
⇒ PA . PB = PC . PD
Hence proved

Question 19.
Solution:
Given : In right ∆ABC, ∠B = 90°
D is a point on hypotenuse AC such that
BD ⊥ AC and DP ⊥ AB and DQ ⊥ BC.
RS Aggarwal Class 10 Solutions Chapter 4 Triangles Ex 4B 22
To prove :
(a) DQ² = DP . QC
(b) DP² = DQ . AP
Proof: AB ⊥ BC and DQ ⊥ BC
AB || DQ
DP ⊥ AB
DP || BC
Now, AB or PB || DQ and BC or BQ || DP BQDP is a rectangle
BQ = DP and BP = DQ
Now, in right ∆BQD
∠1 + ∠2 = 90° …..(i)
Similarly in rt. ∆DQC,
∠3 + ∠4 = 90° (DQ ⊥ BC) …(ii)
and in right ∆BDC,
∠2 + ∠3 = 90° …(iii)
∠BDC = 90° (BD ⊥ AC)
From (i) and (ii),
∠1 = ∠3
and from (ii) and (iii),
∠2 = ∠4
Now, in ∆BQD and ∆DQC
∠1 = ∠3
∠2 = ∠4 (proved)
∆BQD ~ ∆DQC (AA axiom)
\(\frac { BQ }{ DQ }\) = \(\frac { DQ }{ QC }\)
⇒ DQ² = BQ x QC
⇒ DQ² = DP x QC
(b) Similarly, we can prove that
∆PDA ~ ∆PBD
\(\frac { PD }{ PB }\) = \(\frac { AP }{ DP }\)
⇒ DP² = BP x AP
⇒ DP² = DQ . AP (BP = DQ)
Hence proved.

Hope given RS Aggarwal Solutions Class 10 Chapter 4 Triangles Ex 4B are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials Ex 6.5

by

RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials Ex 6.5

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials Ex 6.5

Other Exercises

Using factor theorem, factorize each of the following polynomials:
Question 1.
x3 + 6x2 + 11x + 6
Solution:
RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials Ex 6.5 Q1.1

Question 2.
x3 + 2x2 – x – 2
Solution:
RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials Ex 6.5 Q2.1
RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials Ex 6.5 Q2.2

Question 3.
x3 – 6x2 + 3x + 10
Solution:
RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials Ex 6.5 Q3.1
RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials Ex 6.5 Q3.2

Question 4.
x4 – 7x3 + 9x2 + x- 10
Solution:
RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials Ex 6.5 Q4.1

Question 5.
3x3 – x2 – 3x + 1
Solution:
RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials Ex 6.5 Q5.1

Question 6.
x3 – 23x2 + 142x – 120        [NCERT]
Solution:
RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials Ex 6.5 Q6.1
RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials Ex 6.5 Q6.2

Question 7.
y3 – 7y + 6
Solution:
Let f(y) = y3 – 7y + 6
RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials Ex 6.5 Q7.1

Question 8.
X3 -10x2 – 53x – 42
Solution:
RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials Ex 6.5 Q8.1
RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials Ex 6.5 Q8.2

Question 9.
y3 – 2y2– 29y – 42
Solution:
RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials Ex 6.5 Q9.1
RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials Ex 6.5 Q9.2

Question 10.
2y3 – 5y2 – 19y + 42
Solution:
RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials Ex 6.5 Q10.1
RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials Ex 6.5 Q10.2

Question 11.
x3 + 132 + 32x + 20      [NCERT]
Solution:
RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials Ex 6.5 Q11.1
RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials Ex 6.5 Q11.2

Question 12.
x3 – 3x2 – 9x – 5 [NCERT]
Solution:
RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials Ex 6.5 Q12.1
RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials Ex 6.5 Q12.2

Question 13.
2y3+ y2 – 2y – 1      [NCERT]
Solution:
RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials Ex 6.5 Q13.1

Question 14.
x3 – 2x2 – x + 2
Solution:
RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials Ex 6.5 Q14.1

Question 15.
Factorize each of the following polynomials:
(i) x3 + 13x2 + 31x – 45 given that x + 9 is a factor
(ii) 4x3 + 20x2 + 33x + 18 given that 2x + 3 is a factor
Solution:
RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials Ex 6.5 Q15.1
RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials Ex 6.5 Q15.2
RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials Ex 6.5 Q15.3

Question 16.
x4 – 2x3 – 7x2 + 8x + 12
Solution:
RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials Ex 6.5 Q16.1
RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials Ex 6.5 Q16.2

Question 17.
x4 + 10x3 + 35x2 + 50x + 24
Solution:
RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials Ex 6.5 Q17.1
RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials Ex 6.5 Q17.2

Question 18.
2x4 – 7x3 – 13x2 + 63x – 45
Solution:
RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials Ex 6.5 Q18.1
RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials Ex 6.5 Q18.2
RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials Ex 6.5 Q18.3

Hope given RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials Ex 6.5 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

NCERT Exemplar Solutions for Class 9 Science Chapter 2 Is Matter Around Us Pure

by

NCERT Exemplar Solutions for Class 9 Science Chapter 2 Is Matter Around Us Pure

These Solutions are part of NCERT Exemplar Solutions for Class 9 Science . Here we have given NCERT Exemplar Solutions for Class 9 Science Chapter 2 Is Matter Around Us Pure.

Question 1.
Which of the following statements are true for pure substances ?
(i) Pure substances contain only one kind of particles
(ii) Pure substances may be compounds or mixtures
(iii) Pure substances have the same composition throughout
(iv) Pure substances can be exemplified by all elements other than nickel.
(a) (i) and (ii)            (b) (i) and (iii)
(c) (iii) and (iv)          (d) (ii) and (iii).
Correct Answer:
(b) Both these statements are correct.

More Resources

Question 2.
Rusting of an article made up of iron is called
(a) corrosion and it is a physical as well as chemical change
(b) dissolution and it is a physical change
(c) corrosion and it is a chemical change {d) dissolution and it is a chemical change.
Correct Answer:
(c) corrosion and it is a chemical change.

Question 3.
A mixture of sulphur and carbon disulphide is
(a) heterogeneous and shows Tyndall effect
(b) homogeneous and shows Tyndall effect
(c) heterogeneous and does not show Tyndall effect
(d) homogeneous and does not show Tyndall effect.
Correct Answer:
(d) Sulphur dissolves in carbon disulphide to form a solution which is homogeneous in nature. It does not show any Tyndall effect.

Question 4.
Tincture of iodine has antiseptic properties. This solution is made by dissolving
(a) iodine in benzene
(b) iodine in ether
(c) iodine in water
(d) iodine in alcohol.
Correct Answer:
(d) Tincture of iodine is a dilute solution of iodine formed by dissolving iodine in ethyl alcohol also called alcohol.

Question 5.
Which of the following are homogeneous mixtures in nature ?
(i) ice
(ii) wood
(iii) soil
(iv) air.
(a) (i) and (iii)        (b) (ii) and (iv)
(c) (i) and (iv)        (d) (iii) and (iv).
Correct Answer:
(c) Both ice and air are homogeneous mixtures.

Question 6.
Which of the following are physical changes ?
(i) Melting of iron metal
(ii) Rusting of iron
(iii) Bending of an iron rod
(iv) Drawing a wire of iron metal
(a) (i), (ii) and (iii)          (b) (i), (ii) and (iv)
(c) (i), (iii) and (iv)         (d) (ii), (iii) and (iv).
Correct Answer:
(c) All the three are examples of physical changes.

Question 7.
Which of the following are chemical changes ?
(i) Decaying of wood
(ii) Burning of wood
(iii) Growth of wood in a tree
(iv) Hammering of a nail into a piece of wood.
(a) (i) and (ii)             (b) (ii) and (iv)
(c) (iii) and (iv)           (d) (i), (ii) (iiii).
Correct Answer:
(d) All the three are chemical changes.

Question 8.
Two substances, A and B were made to react to form a third substance, A2B according to the following reaction
2A + B —> A2B
Which of the following statements concerning this
reaction are incorrect ?
(i) The product A2B shows the properties of substances A and B
(ii) The product will always have a fixed composition
(iii) The product so formed cannot be classified as a compound
{iv) The product so formed is an element.
(a) (i), (ii) and (iii)           (b) (ii), (iii) and (iv)
(c) (i), (iii) and (iv)          (d) (ii), (iii) and (iv).
Correct Answer:
(c) Except for (ii) all other statements are incorrect.

Question 9.
Two chemical species X and Y combine together to form a product P which contains both X and Y
X + Y —> P
X and Y cannot be broken down into simpler substances by simple chemical reactions. Which of the following concerning the species X, Y and P are correct ?
(i) P is a compound
(ii) X and Y are compounds
(iii) X and Y are elements
(iv) P has a fixed composition
(a) (i), (ii) and {iii)               (b) (i), (ii) and (iv)
(c) (ii), (iii) and (iv)              (d) (i), (iii) and (iv).
Correct Answer:
(d) All these statements are correct.

Short Answer Questions

Question 10.
Suggest separation technique(s) one would need to employ to separate the following mixtures.

  1. Mercury and water
  2. Potassium chloride and ammonium chloride
  3. Common salt, water and sand
  4. Kerosene oil, water and salt.

Answer:

  1. Separation can be done with a separating funnel. Mercury being heavy forms lower layer.
  2. Sublimation can be used. Ammonium chloide sublimes.
  3. Filtration followed by crystallisation techniques can be used here. Sand can be removed as an insoluble residue upon filtration. Upon evaporating the filtrate in a china dish to about one third followed by slow colling crystals of common salt (NaCl) are formed.
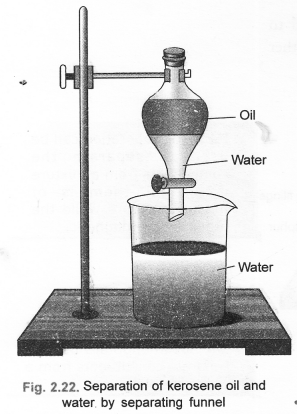
  4. Kerosene oil can be separated with a separating funnel. Water and salt can be separated either by distillation (water distils) or by evaporation (water evaporates). Salt is left behind as residue.

Question 11.
Which of the tubes {a) and {b) will be more effective as a condenser in the distillation apparatus ?
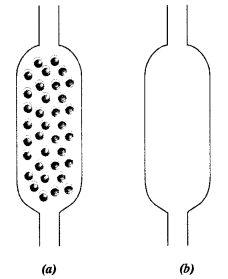
NCERT Exemplar Solutions for Class 9 Science Chapter 2 Is Matter Around Us Pure image - 1
Answer:
Condenser
(a) has a number of bends or obstructions. It will provide more opportunity to vapours to condense and act as a better condenser than
(b) which has no such obstructions.

Question 12.
Salt can be recovered from its solution by evaporation. Suggest some other technique for the same ?
Answer:
Crystallisation technique can also be used. For example, both these can be used to separate salts like sodium chloride (common salt) and potasium nitrate (nitre) from their aqueous solutions.

Question 13.
Sea-water can be classified as homogeneous as well as heterogeneous mixture. Comment.
Answer:
The sample of sea water from mid stream is transparent and has certain salts dissolved in water. It is therefore, homogeneous., However, the sample collected from near the seashore contains mud and many suspended particles. It is therefore, heterogeneous in nature.

Question 14.
While diluting a solution of salt in water, a student by mistake added acetone (boiling point 56°C). What technique can be employed to get back acetone ? Justify your choice.
Answer:
Acetone can be recovered by carrying out the distillation in a distillation flask. Its vapours will rise since it is volatile, get condensed and collected in a receiver. Salt being non-volatile in nature remains in the flask.

Question 15.
What would you observe when
(a) a saturated solution of potassium chloride prepared at 60°C is allowed to cool to room temperature.
(b) an aqueous sugar solution is heated to dryness
(c) a mixture of iron filings and sulphur powder is heated strongly.
Answer:
(a) Upon cooling, crystals of potassium chloride would separate.
(b) Initially, entire water slowly gets removed. Upon further heating, sugar gets charred and burning smell will be noticed.
(c) Iron sulphide is formed as a greyish black residue.

Question 16.
Explain why particles of a colloidal solution do not settle down when left undisturbed while in the case of a suspension, they do.
Answer:
In a colloidal solution, the particle size is smaller as compared to particle size in a suspension. The effect of gravity on these particles is less than in a suspension. Therefore, the particles in a suspension settle under the influence of gravity while they remain dispersed in a colloidal solution.

Question 17.
Smoke and fog both are aerosols. In what way are they different ?
Answer:
Air is the dispersion medium in both the cases. However, dispersed phases are not the same. In smoke, carbon particles act as the dispersed phase while water drops represent the dispersed phase in fog.

Question 18.
Classify the following as physical or chemical properties (CBSE 2012)

  1. The composition of a sample of steel is : 98% iron. 1-5% carbon and 0-5% other elements.
  2. Zinc dissolves in hydrochloric acid with the evolution of hydrogen gas.
  3. Metallic sodium is soft enough to be cut with a knife.
  4. Most metal oxides form alkalis on interacting with water.

Answer:

  1. Physical
  2. Chemical
  3. Physical
  4. Chemical.

Question 19.
The teacher instructed three students A’, ‘B’ and ‘C’ respectively to prepare a 50% (mass by volume) solution of sodium hydroxide (NaOH). ‘A’ dissolved 50 g of NaOH in 100 mL of water. ‘B’ dissolved 50 g of NaOH in 100 g of water while ‘C’ dissolved 50 g of NaOH in water to make 100 mL of solution. Which one of them has made the desired solution and why ?
Answer:
The student ‘C’ has prepared the desired solution since it represents mass/volume solution. The student A’ has taken into account volume of the solvent while the student ‘B’ has considered the mass of the solution
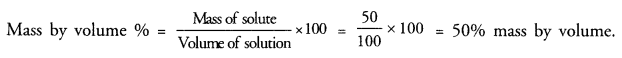
NCERT Exemplar Solutions for Class 9 Science Chapter 2 Is Matter Around Us Pure image - 2

Question 20.
Name the process associated with the following :

  1. Dry ice is kept at room temperature and under one atmospheric pressure.
  2. A drop of ink placed on the surface of water contained in a glass spreads throughout the water.
  3. A potassium permanganate crystal is in a beaker and water is poured into the beaker with stirring.
  4. An acetone bottle is left open and the bottle, becomes empty.
  5. Milk is churned to separate cream from it. .
  6. Settling of sand when a mixture of sand and water is left undisturbed for some time.
  7. Fine beam of light entering through a small hole in a dark room, illuminates the particles in its paths.

Answer:

  1. Sublimation
  2. Diffusion/Sedimentation
  3. Dissolution/Dififusion
  4. Evaporation/Diffusion
  5. Centrifugation
  6. Sedimentation
  7. Scattering of light (Tyndall effect).

Question 21.
You are given two samples of water labelled as A and ‘B’. Sample A boils at 100°C and sample ‘B’ boils at 102°C. Which sample of water will not freeze at 0°C ? Comment.
Answer:
The standard boiling point temperature of water is 100°C. Therefore, the sample v/ith boiling point 100°C represents the pure form of water. The sample with boiling point 102° C is impure. Please note that impurities always raise the boiling point temperatures of liquids and lower their freezing point temperature. Therefore, the sample ‘B’ will freeze before 0°C.

Question 22.
What are the favourable qualities given to gold when it is alloyed with copper or silver for the purpose of making ornaments ?
Answer:
Pure gold (24 carats) is very soft and cannot be used for making ornaments. It is alloyed with a small quantity of copper or silver and becomes hard (22 carats). It can be drawn into wires (becomes ductile) or beaten into fine sheets (becomes malleable). It can, therefore, be used for making ornaments.

Question 23.
An element is sonorous and highly ductile. Under which category would you classify this element ? What other characteristics do you expect the element to possess ?
Answer:
The element is a metal. It is expected to possess the important characteristics of the metals.
Semi-Metals or Metalloids
There are a few elements which possess the characteristics of both metals and non-metals. These are actually border-line elements and are known as semi-metals. Semi-metals are also called metalloids. A few common examples are : Silicon, Arsenic, Antimony and Bismuth.

Question 24.
Give an example each for the mixture having the following characteristics. Suggest a suitable method to separate the components of these mixtures

  1. A volatile and a non-volatile component.
  2. Two volatile components with appreciable difference in boiling points.
  3. Two immiscible liquids.
  4. One of the components changes directly from solid to gaseous state.
  5. Two or more coloured constituents soluble in same solvent.

Answer:

  1. A mixture of naphthalene (volatile) and common salt (non-volatile). The separation can be done by sublimation.
  2. A mixture of acetone (boiling point = 56°C) and water (boiling point = 100°C) separation can be done by distillation.
  3. A mixture of kerosene oil and water. Separation can be done in a separating funnel.
  4. Same as in (a).
  5. A mixture of blue/black ink. Separation can be done by chromatography.

Question 25.
Fill in the blanks

  1. A colloid is a …………… mixture and its components can be separated by the technique known as …………… .
  2. Ice, water and water vapours look different and display different …………… properties but they are the …………… same.
  3. A mixture of chloroform and water taken in a separating funnel is mixed and left undisturbed for some time. The upper layer in the separating funnel will be of …………… and the lower layer will be that of …………… .
  4. A mixture of two or more miscible liquids for which the difference in the boiling points is less than 25 K, can be separated by the process called …………… .
  5. When light is passed through water containing a few drops of milk, it shows a bluish tinge. This is due to the …………… of light by milk and the phenomenon is called …………… . This indicates that milk is a …………… solution.

Answer:

  1. heterogenous, centrifugation
  2. physical, chemically
  3. water, chloroform (density of water is less than that of chloroform)
  4. fractional distillation
  5. scattering, Tyndall effect, colloidal (also called emulsion).

Question 26.
Sucrose (sugar) crystals obtained from sugarcane and beetroot are mixed together. Will it be a pure substance or a mixture ? Give reasons for the same.
Answer:
Both are chemically the same and represent a single chemical compound. Flence, they are pure substance.

Question 27.
Give some examples of Tyndall effect observed in your surroundings.
Answer:

  1. Tyndall effect can be observed when sun light is made to enter the room in the morning time through a small slit. Dust particles with zig-zag motion can be seen.
  2. Tyndall effect can be seen when sun light passes through the canopy of a dense forest.

Question 28.
Can we separate a mixture of alcohol and water by the use of a separating funnel ? If not, suggest an alternate method.
Answer:
No, the mixture of alcohol and water cannot be separated by the use of separating funnel because the two are completely miscible with each other. The separation can be done by fractional distillation.
The student should have dissolved the impure sample in carbon disulphide. It is a liquid in which sulphur completely dissolves while iron does not. From the solution, sulphur can be recovered with the help of crystallization process.

Question 29.
On heating, calcium carbonate gets converted into calcium oxide and carbon dioxide.

  1. Is this a physical or a chemical change ?
  2. Can you prepare one acidic and one basic solution by using the products formed in the above process ? If so, write the chemical equation involved.

Answer:

  1. It is chemical change. The chemical equation for the reaction is :
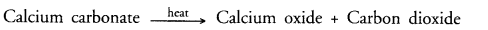
    NCERT Exemplar Solutions for Class 9 Science Chapter 2 Is Matter Around Us Pure image - 3
  2. By adding water to calcium oxide taken in a test tube, a basic solution results. It contains calcium hydroxide
    Calcium oxide + Water —-> Calcium hydroxide
    By passing carbon dioxide through water taken in a tube, carbonic acid is formed. The solution is of acidic nature
    Carbon dioxide + Water —-> Carbonic acid

Note:
All the three chemical equations are word equations. Symbol equations can also be written for these.
For example,
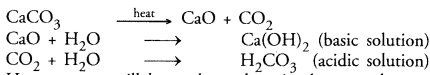
NCERT Exemplar Solutions for Class 9 Science Chapter 2 Is Matter Around Us Pure image - 4
However, you will learn about these in the next class.

Question 30.
Non metals are usually poor conductors of heat and electricity. They are non-lustrous, non-sono- rous, non-malleable and are coloured.

  1. Name a lustrous non-metal.
  2. Name a non-metal which exists as a liquid at room temperature.
  3. The allotropie form of a non-metal is a good conductor of electricity. Name the allotope.
  4. Name a non-metal which is known to form the largest number of compounds.
  5. Name a non-metal other than carbon which shows allotropy.
  6. Name a non-metal which is required for combustion.

Answer:

  1. Graphite (Carbon)
  2. Bromine
  3. Graphite(Carbon)
  4. Carbon
  5. Silicon
  6. Coke (Carbon).

Question 31.
Classify the substances given in the figure into elements and compounds.
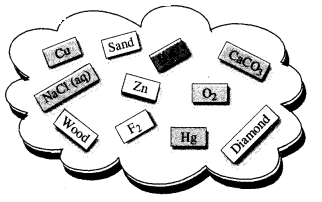
NCERT Exemplar Solutions for Class 9 Science Chapter 2 Is Matter Around Us Pure image - 5
Answer:
Elements : Cu, Zn, Hg, Diamond.
Compounds : H2O, CaCO3, O2, F2
Note: Sand, NaCl (aq) and wood are the examples of mixtures.

Question 32.
Which of the following are not compounds ?

  1. Chlorine gas
  2. Potassium chloride
  3. Iron
  4. Iron sulphide
  5. Aluminium
  6. Iodine
  7. Carbon
  8. Carbon monoxide
  9. Sulphur powder.

Answer:
Iron, aluminium, carbon and sulphur powder are not compounds. These are elements.

Long Answer Questions

Question 33.
Fractional distillation is suitable for separation of miscible liquids with a boiling point difference of about 25 K or less. What part of fractional distillation apparatus makes it efficient and possesses an advantage over a simple distillation process. Explain using a diagram.
Answer:
It is the fractionating column which fits into the distillation flask. It is packed with a number of glass beads. A the vapours of both the volatile liquids rise upwards in the distillation flask, the beads obstruct their movement i.e. it slows down. The vapours of higher boiling liquid condense to the liquid state and in doing so they release certain energy’ known as latent heat of condensation. The energy which is released is taken up by the molecules of lower boiling liquid. As a result, they vapourise more quickly and pass through the water condenser and condense as a liquid in the receiver. The higher boiling liquid remains in the distillation flask only. For further details about the fractional distillation
NCERT Exemplar Solutions for Class 9 Science Chapter 2 Is Matter Around Us Pure image - 6

Question 34.
(a) Under which category of mixtures will you classify alloys and why ?
(b) A solution is always a liquid. Comment.
(c) Can a solution be heterogeneous ?
Answer:
(a) Aloys are regarded as homogeneous mixtures since the constituting elements are uniformly mixed in an alloy.
(b) This statement is not true. There may also be solid solutions (solid acts as solvent) and gaseous solutions (gas acts as solvent).
(c) No, a solution is always a homogeneous mixture of two or more substances.

Question 35.
Iron filings and sulphur were mixed together and divided into two parts ‘A’ and ‘B’. Part ‘A’ was heated strongly while Part ‘B’ was not heated. Dilute hydrochloric acid was added to both the Parts and evolution of gas was seen in both the cases. How will you identify the gases evolved ?
Answer:

  1. In part A iron and sulphur will remain as such in the form of a mixture. On adding dilute hydrochlo¬ride acid iron will react to evolve hydrogen gas. The gas can be tested by bringing a burning splinter near its mouth. It will burn with a pop sound.
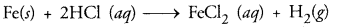
    NCERT Exemplar Solutions for Class 9 Science Chapter 2 Is Matter Around Us Pure image - 7
  2. In part ‘B’ iron and sulphur will combine on heating to form greyish black solid known as iron sulphide.
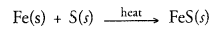
    NCERT Exemplar Solutions for Class 9 Science Chapter 2 Is Matter Around Us Pure image - 8
  3. When dilute hydrocloric acid is added to the greyish black mass taken in a tube, a gas with foul smell similar to that of the rotton eggs will evolve. This is hydrogen sulphide (H2S) Cover or Lid
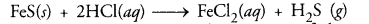
    NCERT Exemplar Solutions for Class 9 Science Chapter 2 Is Matter Around Us Pure image - 9

Question 36.
A child wanted to separate the mixture of dyes constituting a sample of ink. He marked a line by the ink on the filter paper and placed the filter paper in a glass containing water as shown in the fig . The filter paper was removed when the water moved near the top of the filter paper.
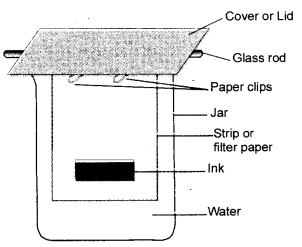
NCERT Exemplar Solutions for Class 9 Science Chapter 2 Is Matter Around Us Pure image - 10

  1. What would you expect to see, if the ink contains three different coloured components ?
  2. Name the technique used by the child.
  3. Suggest one more application of this technique

Answer:

  1. Three different bands will be seen on the filter papers.
  2. The technique is known as paper chromatography.
  3. It can be used to separate the coloured pigments from chlorophyll.

Question 37.
A group of students took an old shoe box and covered it with a black paper from all sides. They fixed a source of light (a torch) at one end of the box by making a hole in it and made another hole on the other side to view the light. They placed a milk sample contained in a beaker/tumbler in the box as shown in the figure.
They were amazed to see the milk taken in the tumbler was illuminated. They tried the same activity by taking a salt solution but found that light simply passed through it ?
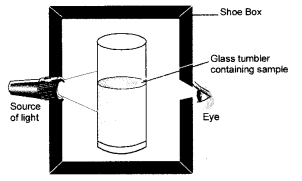
NCERT Exemplar Solutions for Class 9 Science Chapter 2 Is Matter Around Us Pure image - 11

  1. Explain why the milk sample was illuminated. Name the phenomenon involved.
  2. Same results were not observed with a salt solution. Explain.
  3. Can you suggest two more solutions which would show the same effect as shown by the milk solution ?

Answer:

  1. Milk sample is a colloidal sol also called emulsion. It got illuminated because of the scattering of light on passing through it. The phenomenon is known as Tyndall effect.
  2. The salt solution is a true solution and not a colloidal solution. It will not show any Tyndall effect.
  3. A solution of sulphur in water and a solution of starch in water.

Question 38.
Classify each of the following, as a physical or a chemical change. Give reasons.

  1. Drying of a shirt in the sun.
  2. Rising of hot air over a radiator.
  3. Burning of kerosene in a lantern.
  4. hange in the colour of black tea on adding lemon juice to it.
  5. Churning of milk cream to get butter.

Answer:

  1. It is a physical change. Moisture or water drops present on the shirt will evaporate or change into vapours.
  2. It is a physical change. On cooling, the level of air over the radiator will fall.
  3. It is a chemical change. The hydrocarbons present in kerosene will react chemically with oxygen to form new products.
  4. It is a chemical change. The acid present in lemon juice will react with the constituents (e.g. caffeine) present in black tea.
  5. It is a physical change. However, butter will not change to milk so easily.

Question 39.
During an experiment the students were asked to prepare a 10% (Mass/Mass) solution of sugar in water. Ramesh dissolved 10 g of sugar in 100 g of water while Sarika prepared it by dissolving 10 g of sugar in water to make 100 g of the solution.
(a) Are the two solutions of the same concentration
(b) Compare the mass % of the two solutions.
Answer:
(a) No, the two solutions have different concentrations.
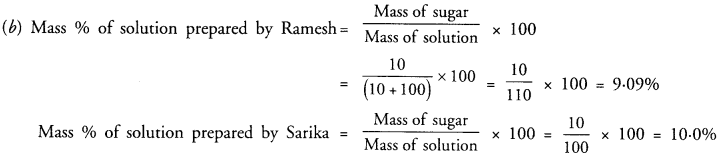
NCERT Exemplar Solutions for Class 9 Science Chapter 2 Is Matter Around Us Pure image - 12

Question 40.
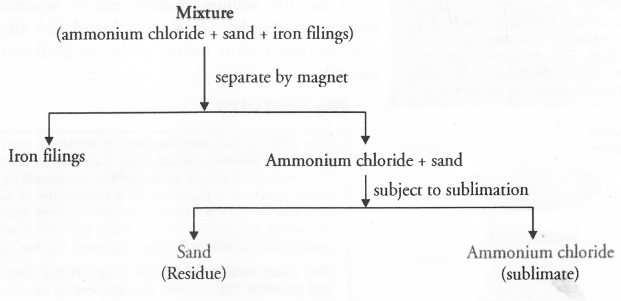
You are provided with a mixture containing sand, iron filings, ammonium chloride and sodium chloride. Describe the procedure you would use to separate these constituents from the mixture ?
Answer:
Separate the constituents from a mixture containing ammonium chloride, sand and iron-filings.
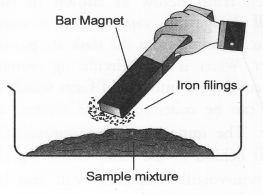
NCERT Exemplar Solutions for Class 9 Science Chapter 2 Is Matter Around Us Pure image - 13
Place the mixture on a paper or petridish. Move a magnet over it. Iron filings get attached to the magnet. Scrap off iron filings from the magnet and collect them separately. Transfer the remaining mixture to a china dish and subject it to the sublimation process. Ammonium chloride forms the sublimate while sand is left as residue in the dish.
NCERT Exemplar Solutions for Class 9 Science Chapter 2 Is Matter Around Us Pure image - 14

Question 41.
Arun has prepared 0301% (by mass) solution of sodium chloride in water. Which of the following correctly represents the composition of the solution ?
(a) 1.00 g of NaCl + 100 g of water
(b) 0.11 g of NaCl + 100 g of water
(c) 0.01 g of NaCl + 99.99 g of water
(d ) 0.10 g of NaCl + 99.90 g of water.
Answer:
By definition 0.01% (by mass) solution means that 0.01 g of sodium chloride is dissolved in 0.99 g (by mass) of water. Therefore (c) represents the correct composition of the solution. This can be further verified as follows :
NCERT Exemplar Solutions for Class 9 Science Chapter 2 Is Matter Around Us Pure image - 15

Question 42.
Calculate the mass of sodium sulphate required to prepare its 20% (mass percent) solution in 100 g of water ?
Answer:
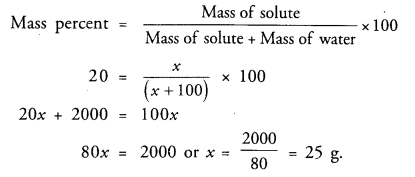
NCERT Exemplar Solutions for Class 9 Science Chapter 2 Is Matter Around Us Pure image - 16

Hope given NCERT Exemplar Solutions for Class 9 Science Chapter 2 Is Matter Around Us Pure are helpful to complete your science homework.

If you have any doubts, please comment below. Learn Insta try to provide online science tutoring for you.

RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.4

by

RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.4

These Solutions are part of RD Sharma Class 8 Solutions. Here we have given RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.4

Other Exercises

Question 1.
Write the possible unit’s digits of the square root of the following numbers. Which of these numbers are odd square roots ?
(i) 9801
(ii) 99856
(iii) 998001
(iv) 657666025
Solution:
(i)  In \(\sqrt { 9801 }\) ∴ the units digits is 1, therefore, the units digit of the square root can be 1 or 9
(ii) In \(\sqrt { 799356 }\) ∴ the units digit is 6
∴ The units digit of the square root can be 4 or 6
(iii) In \(\sqrt { 7998001 }\) ∴ the units digit is 1
∴ The units digit of the square root can be 1 or 9
(iv) In 657666025
∴ The unit digit is 5
∴ The units digit of the square root can be 5

Question 2.
Find the square root of each of the following by prime factorization.
(i) 441
(ii) 196
(iii) 529
(iv) 1764
(v) 1156
(vi) 4096
(vii) 7056
(viii) 8281
(ix) 11664
(x) 47089
(xi) 24336
(xii) 190969
(xiii) 586756
(xiv) 27225
(xv) 3013696
Solution:
RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.4 1
RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.4 2
RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.4 3
RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.4 4
RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.4 5
RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.4 6
RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.4 7

Question 3.
Find the smallest number by which 180 must be multiplied so that it becomes a perfect square. Also, find the square root of the perfect square so obtained.
Solution:
Factorising 180,
RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.4 8
180 = 2 x 2 x 3 x 3 x 5
Grouping the factors in pairs we see that factor 5 is left unpaired.
∴ Multiply 180 by 5, we get the product 180 x 5 = 900
Which is a perfect square
and square root of 900 = 2 x 3 x 5 = 30

Question 4.
Find the smallest number by which 147 must be multiplied so that it becomes a perfect square. Also, find the square root of the number so obtained.
Solution:
Factorising 147,
RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.4 9
147 = 3 x 7×7
Grouping the factors in pairs of the equal factors, we see that one factor 3 is left unpaired
∴ Multiplying 147 by 3, we get the product 147 x 3 = 441
Which is a perfect square
and its square root = 3×7 = 21

Question 5.
Find the smallest number by which 3645 must be divided so that it becomes a perfect square. Also, find the square root of the resulting number.
Solution:
Factorising 3645
RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.4 10
3645 = 3 x 3 3 x 3 x 3 x 3 x 5
Grouping the factors in pair of the equal factors, we see t at one factor 5 is left unpaired
∴ Dividing 3645 by 5, the quotient 729 will be the perfect square and square root of 729 = 27

Question 6.
Find the smallest number by which 1152 must be divided so that it becomes a perfect square. Also, find the square root of the number so obtained.
Solution:
Factorsing 1152,
RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.4 11
1152 = 2 x 2 x 2 x 2 x 2 x 2 x 2 x 3 x 3
Grouping the factors in pairs of the equal factors, we see that factor 2 is left unpaired.
∴ Dividing by 2, the quotient 576 is a perfect square .
∴ Square root of 576, it is 24

Question 7.
The product of two numbers is 1296. If one number is 16 times the others find the numbers.
Solution:
Product of two numbers = 1296
Let one number = x
Second number = 16x
RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.4 12
∴ First number = 9
and second number = 16 x 9 = 144

Question 8.
A welfare association collected Rs. 202500 as donation from the residents. If each paid as many rupees as there were residents find the number of residents.
Solution:
Total donation collected = Rs. 202500
Let number of residents = x
Then donation given by each resident = Rs. x
∴ Total collection = Rs. x x x
RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.4 13

Question 9.
A society collected Rs. 92.16. Each member collected as many paise as there were members. How many members were there and how much did each contribute?
Solution:
Total amount collected = Rs. 92.16 = 9216 paise
Let the number of members = x
Then amount collected by each member = x
paise
RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.4 14
∴ Number of members = 96
and each member collected = 96 paise

Question 10.
A school collected Rs. 2304 as fees from its students. If each student paid as many paise as there were students in the school, how many students were there in the school ?
Solution:
Total fee collected = Rs. 2304
Let number of students = x
Then fee paid by each student = Rs. x
∴ x x x = 2304 => x2 = 2304
∴ x = \(\sqrt { 2304 }\)
RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.4 15

Question 11.
The area of a square field is 5184 m2. A rectangular field, whose length is twice its breadth has its perimeter equal to the perimeter of the square field. Find the area of the rectangular field.
Solution:
The area of a square field = 5184 m2
Let side of the square = x
RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.4 16
∴ side of square= 72 m
∴ Perimeter, of square field = 72 x 4 m = 288 m
Perimeter of rectangle = 288 m
Let breadth of rectangular field (b) = x
Then length (l) = 2x
∴ Perimeter = 2 (l + b)
= 2 (2x + x) = 2 x 3x = 6x
= 2 (2x + x) = 2 x 3x = 6x
RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.4 17
∴ Length of rectangular field = 2x = 2 x 48 = 96 m
and breadth = 48 m
and area = l x b = 96 x 48 m2
= 4608 m2

Question 12.
Find the least square number, exactly divisible by each one of the numbers :
(i) 6, 9,15 and 20
(ii) 8,12,15 and 20
Solution:
RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.4 18
LCM of 6, 9, 15, 20 = 2 x 3 x 5 x 3 x 2 = 180
=2 x 2 x 3 x 3 x 5
We see that after grouping the factors in pairs, 5 is left unpaired
∴ Least perfect square = 180 x 5 = 900
RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.4 19
We see that after grouping the factors,
factors 2, 3, 5 are left unpaired
∴ Perfect square =120 x 2 x 3 x 5 = 120 x 30 = 3600

Question 13.
Find the square roots of 121 and 169 by the method of repeated subtraction.
Solution:
RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.4 20

Question 14.
Write the prime factorization of the following numbers and hence find their square roots. ^
(i) 7744
(ii) 9604
(iii) 5929
(iv) 7056
Solution:
Factorization, we get:
(i) 7744 = 2 x 2 x 2 x 2 x 2 x 2 x 11 x 11
RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.4 21
Grouping the factors in pairs of equal factors,
RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.4 22
Question 15.
The students of class VIII of a school donated Rs. 2401 for PM’s National Relief Fund. Each student donated as many rupees as the number of students in the class. Find the number of students in the class.
Solution:
Total amount of donation = 2401
Let number of students in VIII = x
∴ Amount donoted by each student = Rs. x
RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.4 23

Question 16.
A PT teacher wants to arrange maximum possible number of 6000 students in a Held such that the number of rows is equal to the number of columns. Find the number of rows if 71 were left out after arrangement.
Solution:
Number of students = 6000
Students left out = 71
∴ Students arranged in a field = 6000 – 71=5929
RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.4 24

Hope given RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.4 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.