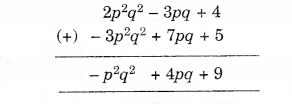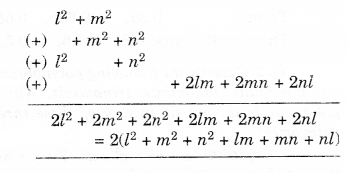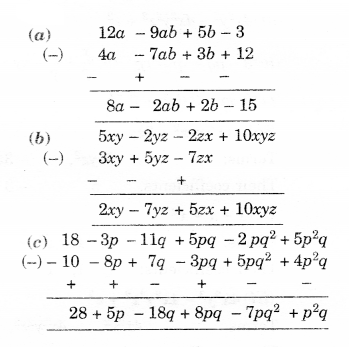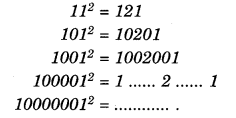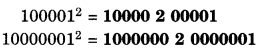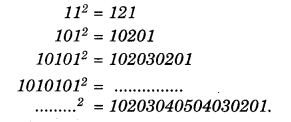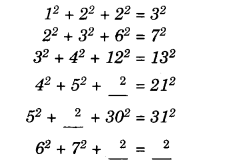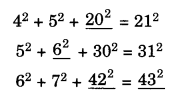NCERT Solutions for Class 8 Maths

NCERT Solutions for Class 8 Maths Chapter 10 Visualising Solid Shapes Ex 10.1 are part of NCERT Solutions for Class 8 Maths. Here we have given NCERT Solutions for Class 8 Maths Chapter 10 Visualising Solid Shapes Ex 10.1.

• Visualising Solid Shapes Class 8 Ex 10.2
• Visualising Solid Shapes Class 8 Ex 10.3

NCERT Solutions for Class 8 Maths Chapter 10 Visualising Solid Shapes Ex 10.1

Question 1.
For each of the given solid, the two views are given. Match for each solid the corresponding top and front views. The first one is done for you.

Solution.

Question 2.
For each of the given solid, the three views are given. Identify for each solid the corresponding top, front and side views.

Solution.

Question 3.
For each given solid, identify the top view, front view, and side view.

Solution.

Question 4.
Draw the front view, side view and top view of the given objects,

Solution.

We hope the NCERT Solutions for Class 8 Maths Chapter 10 Visualising Solid Shapes Ex 10.1 help you. If you have any query regarding NCERT Solutions for Class 8 Maths Chapter 10 Visualising Solid Shapes Ex 10.1, drop a comment below and we will get back to you at the earliest.

NCERT Solutions for Class 8 Maths Chapter 9 Algebraic Expressions and Identities Ex 9.1 are part of NCERT Solutions for Class 8 Maths. Here we have given NCERT Solutions for Class 8 Maths Chapter 9 Algebraic Expressions and Identities Ex 9.1.

• Algebraic Expressions and Identities Class 8 Ex 9.2
• Algebraic Expressions and Identities Class 8 Ex 9.3
• Algebraic Expressions and Identities Class 8 Ex 9.4
• Algebraic Expressions and Identities Class 8 Ex 9.5

NCERT Solutions for Class 8 Maths Chapter 9 Algebraic Expressions and Identities Ex 9.1

Question 1.
Identify the terms, their coefficients for each of the following expressions:
(i) \({ 5xyz }^{ 2 }-3zy\)
(ii) \(1+x+{ x }^{ 2 }\)
(iii) \(4{ x }^{ 2 }{ y }^{ 2 }-4{ x }^{ 2 }{ y }^{ 2 }{ z }^{ 2 }+{ z }^{ 2 }\)
(iv) 3 – pq + qr – rp
(v) \(\frac { x }{ 2 } +\frac { y }{ 2 } -xy\)
(vi) 0.3a – 0.6ab + 0.5b.
Solution.
(i) \({ 5xyz }^{ 2 }-3zy\)

(ii) \(1+x+{ x }^{ 2 }\)

(iii) \(4{ x }^{ 2 }{ y }^{ 2 }-4{ x }^{ 2 }{ y }^{ 2 }{ z }^{ 2 }+{ z }^{ 2 }\)

(iv) 3 – pq + qr – rp

(v) \(\frac { x }{ 2 } +\frac { y }{ 2 } -xy\)

(vi)0.3a – 0.6ab + 0.5b.

Question 2.
Classify the following polynomials as monomials, binomials, trinomials. Which polynomials do not fit in any of these three categories?

Solution.

Question 3.
Add the following.
(i) ab – be, be – ca, ca – ab
(ii) a -b + ab, b – c + be, c – a + ac
(iii) \(2{ p }^{ 2 }{ q }^{ 2 }-3pq+4,\quad 5+7pq-3{ p }^{ 2 }{ q }^{ 2 }\)
(iv) \({ l }^{ 2 }+{ m }^{ 2 },\quad { m }^{ 2 }+{ n }^{ 2 },\quad { n }^{ 2 }+{ l }^{ 2 }\), 2lm + 2mn + 2nl.
Solution.
(i) ab – be, be – ca, ca – ab

(ii) a -b + ab, b – c + be, c – a + ac

(iii) \(2{ p }^{ 2 }{ q }^{ 2 }-3pq+4,\quad 5+7pq-3{ p }^{ 2 }{ q }^{ 2 }\)

(iv) \({ l }^{ 2 }+{ m }^{ 2 },\quad { m }^{ 2 }+{ n }^{ 2 },\quad { n }^{ 2 }+{ l }^{ 2 }\), 2lm + 2mn + 2nl.

Question 4.
(a) Subtract 4a – 7ab + 3b + 12 from 12a – 9ab + 56 – 3
(b) Subtract 3xy + 5yz – 7zx from 5xy – 2yz – 2zx + 10xyz
(c) Subtract \(4{ p }^{ 2 }q-3pq+5p{ q }^{ 2 }-8p+7q-10\) from \(18-3p-11q+5pq-2p{ q }^{ 2 }+5{ p }^{ 2 }q\)
Solution.

We hope the NCERT Solutions for Class 8 Maths Chapter 9 Algebraic Expressions and Identities Ex 9.1 help you. If you have any query regarding NCERT Solutions for Class 8 Maths Chapter 9 Algebraic Expressions and Identities Ex 9.1, drop a comment below and we will get back to you at the earliest.

NCERT Solutions for Class 8 Maths Chapter 8 Comparing Quantities Ex 8.1 are part of NCERT Solutions for Class 8 Maths. Here we have given NCERT Solutions for Class 8 Maths Chapter 8 Comparing Quantities Ex 8.1.

• Comparing Quantities Class 8 Ex 8.2
• Comparing Quantities Class 8 Ex 8.3

NCERT Solutions for Class 8 Maths Chapter 8 Comparing Quantities Ex 8.1

Question 1.
Find ratio of the following:
(a) Speed of a cycle 15 km per hour to the speed of scooter 30 km per hour.
(b) 5 m to 10 km
(c) 50 paise ₹ 5
Solution.
(a)
Speed of a cycle 15 km per hour to the speed of scooter 30 km per hour
Ratio of the speed of cycle which is 15 km per hour to the speed of scooter which is 30 km per hour
= 15 km per hour : 30 km per hour = 15 : 30
= \(\frac { 15 }{ 30 } =\frac { 1 }{ 2 } \) or 1 : 2

(b)
5 m to 10 km
10 km = 10 x 1000 m = 10000 m
∴ Ratio of 5 m to 10 km
= 5 m : 10 km
= 5 m : 10000 m
= 5 : 10000
= \(\frac { 5 }{ 10000 } =\frac { 1 }{ 2000 } \) or 1 : 2000

(c)
50 paise to ₹ 5
₹ 5 = 5 x 100 = 500 paise
∴ Ratio of 50 paise to ₹ 5
= 50 paise : ₹ 5
= 50 paise : 500 paise
= 50 : 500
= \(\frac { 50 }{ 500 } =\frac { 1 }{ 10 } \) or 1 : 10

Question 2.
Convert the following ratios to percentages:
(a) 3: 4
(b) 2 : 3
Solution.
(a) 3: 4

(b) 2 : 3

Question 3.
72% of 25 students are good in mathematics. How many are not good in Mathematics?
Solution.
Total number of students = 25
Students good in mathematics = 72%
∴ Students who are not good in mathematics
= (100 – 72)% = 28%
∴ Number of those students who are not good in mathematics
= 28% of 25
= \(\frac { 28 }{ 100 } \times 25=7\)
Hence, 7 students are not good in mathematics.

Question 4.
A football team won 10 matches out of the total number of matches they played. If their win percentage was 40, then how many matches did they play in all?
Solution.
∵ If 40 matches were won, then the total number of matches played = 100
∴ If 1 match was won, then the total number of matches played = \(\frac { 100 }{ 40 } \)
∴ If 10 matches were won, then the total number of matches played = \(\frac { 100 }{ 40 } \times 10=25\)
Hence, they played 25 matches in all.
Aliter: According to the question, 40% of (total number of matches) = 10
⇒ \(\frac { 40 }{ 100 } \) x (total number of matches) = 10
⇒ Total number of matches = \(\frac { 10\times 100 }{ 40 } \) = 25
Hence, they played 25 matches in all.

Question 5.
If Chameli had ₹ 600 left after spending 75% of her money, how much did she have in the beginning?
Solution.
Percentage of money left = (100 – 75)% = 25%
∵ If Chameli had ₹ 25 left, then the money she had in the beginning = 100
∴ If Chameli had ₹ 1 left, then the money she had in the beginning = \(\frac { 100 }{ 25 } \)
∴ If Chameli has ₹ 600 left, then the money she had in the beginning = \(\frac { 100 }{ 25 } \times 600=2400\)
Hence, the money she had in the beginning was ₹ 2400.
Aliter:
According to the question, 25% of total money = ₹ 600
⇒ \(\frac { 25 }{ 100 } \) x total money = ₹ 600
⇒ Total money = ₹ \(\frac { 600\times 100 }{ 25 } \) = ₹ 2400
Hence, the money she had in the beginning was ₹ 2400

Question 6.
If 60% of people in a city like a cricket, 30% like football and the remaining like other games then what percent of the people like other games? If the total number of people are 50 lakh, find the exact number who like each type of game.
Solution.
People who like other games = [100 – (60 + 30)]%
= (100 – 90)% = 10%.
Total number of people = 50 lakh
= 5000000
∴ Number of people who like cricket = 60% of 5000000
= 5000000 x \(\frac { 60 }{ 100 } \)
= 3000000 = 30 lakh
Number of people who like football = 30% of 5000000
= 5000000 x \(\frac { 30 }{ 100 } \)
= 1500000 = 15 lakh
Number of people who like the other games
= 10% of 5000000
= 5000000 x \(\frac { 10 }{ 100 } \)
= 5,00,000 = 5 lakh

We hope the NCERT Solutions for Class 8 Maths Chapter 8 Comparing Quantities Ex 8.1 help you. If you have any query regarding NCERT Solutions for Class 8 Maths Chapter 8 Comparing Quantities Ex 8.1, drop a comment below and we will get back to you at the earliest.

NCERT Solutions for Class 8 Maths Chapter 7 Cubes and Cube Roots Ex 7.1 are part of NCERT Solutions for Class 8 Maths. Here we have given NCERT Solutions for Class 8 Maths Chapter 7 Cubes and Cube Roots Ex 7.1.

• Cubes and Cube Roots Class 8 Ex 7.2

NCERT Solutions for Class 8 Maths Chapter 7 Cubes and Cube Roots Ex 7.1

Question 1.
Which of the following numbers are not perfect cubes?
(i) 216
(ii) 128
(iii) 1000
(iv) 100
(v) 46656
Solution.
(i) 216

(ii) 128

(iii) 1000

(iv) 100

(v) 46656

Question 2.
Find the smallest number by which each of the following numbers must be multiplied to obtain a perfect cube.
(i) 243
(ii) 256
(iii) 72
(iv) 675
(v) 100
Solution.
(i) 243

(ii) 256

(iii) 72

(iv) 675

(v) 100

Question 3.
Find the smallest number by which each of the following numbers must be divided to obtain a perfect cube.
(i) 81
(ii) 128
(iii) 135
(iv) 192
(v) 704
Solution.
(i) 81

(ii) 128

(iii) 135

(iv) 192

(v) 704

Question 4.
Parikshit makes a cuboid of plasticine of sides 5 cm, 2 cm, 5 cm. How many such cuboids will he need to form a cube?
Solution.
Volume of a cuboid = 5 x 2 x 5 \({ cm }^{ 3 }\).
Since there is only one 2 and only two 5’s in the prime factorization, so, we need 2 x 2 x 5, i.e., 20 to make a perfect cube. Therefore, we need 20 such cuboids to make a cube.

We hope the NCERT Solutions for Class 8 Maths Chapter 7 Cubes and Cube Roots Ex 7.1 help you. If you have any query regarding NCERT Solutions for Class 8 Maths Chapter 7 Cubes and Cube Roots Ex 7.1, drop a comment below and we will get back to you at the earliest.

NCERT Solutions for Class 8 Maths Chapter 6 Squares and Square Roots Ex 6.1 are part of NCERT Solutions for Class 8 Maths. Here we have given NCERT Solutions for Class 8 Maths Chapter 6 Squares and Square Roots Ex 6.1.

• Squares and Square Roots Class 8 Ex 6.2
• Squares and Square Roots Class 8 Ex 6.3
• Squares and Square Roots Class 8 Ex 6.4

NCERT Solutions for Class 8 Maths Chapter 6 Squares and Square Roots Ex 6.1

Question 1.
What will be the unit digit of the squares of the following numbers ?
(i) 81
(ii) 272
(iii) 799
(iv) 3853
(v) 1234
(vi) 26387
(vii) 52698
(viii) 99880
(ix) 12796
(x) 55555
Solution.
(i) 81
∵ \(1\times 1\)
∴ The unit digit of the square of the number 81 will be 1.

(ii) 272
∵ \(2\times 2\)
∴ The unit digit of the square of the number 272 will be 4.

(iii) 799
∵ \(9\times 9\)
∴ The unit digit of the square of the number 799 will be 1.

(iv) 3853
∵ \(3\times 3\)
∴ The unit digit of the square of the number 3853 will be 9

(v) 1234
∵ \(4\times 4\)
∴ The unit digit of the square of the number 1234 will be 6.

(vi) 26387
∵ \(7\times 7\)
∴ The unit digit of the square of the number 26387 will be 9.

(vii) 52698
∵ \(8\times 8\)
∴ The unit digit of the square of the number 52698 will be 4.

(viii) 99880
∵ \(0\times 0\)
∴ The unit digit of the square of the number 99880 will be 0.

(ix) 12796
∵ \(6\times 6\)
∴ The unit digit of the square of the number 12796 will be 6.

(x) 55555
∵ \(5\times 5\)
∴ The unit digit of the square of the number 55555 will be 5.

Question 2.
The following numbers are obviously not perfect squares. Give reason.
(i) 1057
(ii) 23453
(iii) 7928
(iv) 222222
(v) 64000
(vi) 89722
(vii) 222000
(viii) 505050.
Solution.
(i) 1057
The number 1057 is not a perfect square because it ends with 7 at unit’s place whereas the square numbers end with 0, 1, 4, 5, 6 or 9 at unit’s place.

(ii) 23453
The number 23453 is not a perfect square because it ends with 3 at unit’s place whereas the square numbers end with 0, 1, 4, 5, 6 or 9 at unit’s place.

(iii) 7928
The number 7928 is not a perfect square because it ends with 8 at unit’s place whereas the square numbers end with 0, 1, 4, 5, 6 or 9 at unit’s place.

(iv) 222222
The number 222222 is not a perfect square because it ends with 2 at unit’s place whereas the Square numbers end with 0, 1, 4, 5, 6 or 9 at unit’s place.

(v) 64000
The number 64000 is not a square number because it has 3 (an odd number of) zeros at the end whereas the number of zeros at the end of a square number ending with zeros is always even.

(vi) 89722
The number 89722 is not a square number because it ends in 2 at unit’s place whereas the square numbers end with 0, 1, 4, 5, 6 or 9 at unit’s place.

(vii) 222000
The number 222000 is not a square number because it has 3 (an odd number of) zeros at the end whereas the number of zeros at the end of a square number ending with zeros is always even.

(viii) 505050
The number 505050 is not a square number because it has 1 (an odd number of) zeros at the end whereas the number of zeros at the end of a square number ending with zeros is always even.

Question 3.
The squares of which of the following would be odd numbers ?
(i) 431
(ii) 2826
(iii) 7779
(v) 82004.
Solution.
(i) 431
∵ 431 is an odd number
∴ Its square will also be an odd number.

(ii) 2826
∵ 2826 is an even number
∴ Its square will not be an odd number.

(iii) 7779
∵ 7779 is an odd number
∴ Its square will be an odd number.

(iv) 82004
∵ 82004 is an even number
∴ Its square will not be an odd number.

Question 4.
Observe the following pattern and find the missing digits:

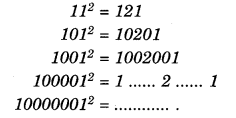
Solution.

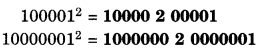
Question 5.
Observe the following pattern and supply the missing numbers:

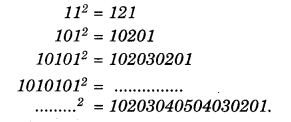
Solution.

Question 6.
Using the given pattern, find the missing numbers:

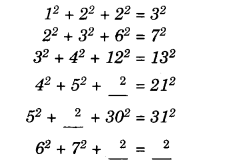
Solution.

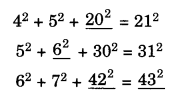
Question 7.
Without adding, find the sum:
(i) 1 + 3 + 5+7 + 9
(ii) 1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 +17 + 19
(iii) 1+3 + 5 + 7 + 9 + 11 + 13 + 15 + 17 + 19 + 21 +23.
Solution.
(i)
l + 3 + 5 + 7 + 9 = sum of first five odd natural numbers = \({ 5 }^{ 2 }\) = 25

(ii)
1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17 + 19 = sum of first ten odd natural numbers = \({ 10 }^{ 2 }\) = 100

(iii)
1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17 + 19 + 21 + 23 = sum of first twelve odd natural numbers = \({ 12 }^{ 2 }\)= 144.

Question 8.
(i) Express 49 as the sum of 7 odd numbers.
(ii) Express 121 as the sum of 11 odd numbers.
Solution.
(i)
49 (= \({ 7 }^{ 2 }\))
= 1 + 3 + 5 + 7 + 9 + 11 + 13

(ii)
121 (= \({ 11 }^{ 2 }\))
= 1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17 + 19 + 21.

Question 9.
How many numbers lie between squares of the following numbers ?
(i) 12 and 13
(ii) 25 and 26
(iii) 99 and 100.
Solution.
(i) 12 and 13
Here, n = 12
∴ 2n = 2 x 12 = 24
So, 24 numbers lie between squares of i the numbers 12 and 13.

(ii) 25 and 26
Here, n = 25
∴ 2n = 2 x 25 = 50
So, 50 numbers lie between squares of the numbers 25 and 26.

(iii) 99 and 100
Here, n = 99
∴ 2n = 2 x 99 = 198
So, 198 numbers lie between squares of of the numbers 99 and 100.

We hope the NCERT Solutions for Class 8 Maths Chapter 6 Squares and Square Roots Ex 6.1 are part help you. If you have any query regarding NCERT Solutions for Class 8 Maths Chapter 6 Squares and Square Roots Ex 6.1 are part, drop a comment below and we will get back to you at the earliest.