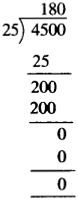NCERT Solutions for Class 6 Maths Chapter 1 Knowing Our Numbers Ex 1.2 are part of NCERT Solutions for Class 6 Maths. Here we have given NCERT Solutions for Class 6 Maths Chapter 1 Knowing Our Numbers Ex 1.2. https://mcqquestions.guru/ncert-solutions-for-class-6-maths-chapter-1-ex-1-2/
| Board |
CBSE |
| Textbook |
NCERT |
| Class |
Class 6 |
| Subject |
Maths |
| Chapter |
Chapter 1 |
| Chapter Name |
Knowing Our Numbers |
| Exercise |
Ex 1.2 |
| Number of Questions Solved |
12 |
| Category |
NCERT Solutions |
NCERT Solutions for Class 6 Maths Chapter 1 Knowing Our Numbers Ex 1.2
Question 1.
A book exhibition was held for four days in a school. The number of tickets sold at the counter on the first, second, third and final day was respectively 1094, 1812, 2050 and 2751. Find the total number of tickets sold on all four days.
Solution :
Number of tickets sold on the first day = 1094
Number of tickets sold on the second day =1812
Number of tickets sold on the third day = 2050
Number of tickets sold on the final day = 2751
Total number of tickets sold on all the four days = 1094 + 1812 + 2050 + 2751 = 7707.
Question 2.
Shekhar is a famous cricket player. He has so far scored 6980 runs in test matches. He wishes to complete 10000 runs. How many more runs does he need?
Solution :
Runs scored so far = 6980
Runs wished to be scored = 10000
Runs needed more = 10000 – 6980 = 3020.
Question 3.
In an election, the successful candidate registered 5,77,500 votes and his nearest rival secured 3,48,700 votes. By what margin did the successful candidate win the election?
Solution :
Votes registered by the successful candidate = 5,77,500
Votes secured by the nearest rival = 3,48.700
Margin by which the successful candidate won the election = 5,77,500 – 3,48,700 = 2,28,800.
Question 4.
Kirti bookstore sold books worth? 2,85,891 in the first week of June and books worth ?. 4,00,768 in the second week of the month. How much was the sale for the two weeks together? In which week was the sale greater and by how much?
Solution :
Sale of books in the first week = ₹ 2,85,891
Sale of books in the second week = ₹ 4,00,768
∴ Sale for the two weeks together = ₹ 2,85,891 + ₹ 4,00,768 = ₹ 6,86,659.
The sale was greater in the second week by ₹ 4,00,768 – ₹ 2,85,891 i.e., by ₹ 1,14,877.
Question 5.
Find the difference between the greatest and least numbers that can be written using the digits 6, 2, 7, 4, 3 each only once.
Sol.
Greatest number that can be written using the digits 6, 2, 7, 4, 3 each only once = 76,432
Least number that can be written using the digits 6, 2, 7, 4, 3 each only once = 23,467
∴ Difference between the greatest and least numbers that can be written using the digits 6,2,7,4, 3 each only once = 76,432 – 23,467 = 52,965.
Question 6.
A machine, on an average, manufactures 2,825 screws a day. How many screws did it produce in the month of January 2006?
Solution :
The number of screws manufactured by the machine a day on an average = 2,825.
Number of days in the month of January 2006 = 31
The number of screws produced by the machine in the month of January 2006 = 2,825 × 31 =87,575.
Question 7.
A merchant had ₹ 78,592 with her. She placed an order for purchasing 40 radio sets at ? 1200 each. How much money will remain with her after the purchase?
Sol.
Money which the merchant had = ₹ 78,592
Cost of 40 radio sets at ? 1200 each = ₹ 1200 × 40 = ₹ 48,000
Money that will remain with the merchant after the purchase = ₹ 78,592 – ₹ 48,000 = ₹ 30,592.
Question 8.
A student multiplied 7236 by 65 instead of multiplying by 56. By how much was his answer greater than the. correct answer?
[Hint: Do you need to do both the multiplications?]
Solution :
The wrong answer was greater than the correct answer by
= 7236 × 65 – 7236 × 56
= 7236 × (65 – 56)
= 7236 × 9 = 65.124
Question 9.
To stitch a shirt, 2 m 15 cm cloth is needed. Out of 40 m cloth, how many shirts can be stitched and how much cloth will remain ?
[Hint: convert data in cm.]
Solution :
2 m 15 cm = 2 m + 15 cm = 2 × 100 cm + 15 cm = 200 cm + 15 cm = 215 cm
40 m = 40 × 100 cm = 4000 cm

Hence, 18 shirts can be stitched and 130 cm,
i. e., 1 m 30 cm cloth will remain.
Question 10.
Medicine is packed in boxes, each weighing 4 kg 500 g. Mow many such boxes can be loaded in a van which cannot carry beyond 800 kg?
Solution :
4 kg 500 g = 4 kg + 500 g
= 4 × 1000 g + 500 g
= 4000 g + 500 g
= 4500 g 800 kg
= 800 × 1000 g = 800000 g

Hence, 177 such boxes can be loaded.
Question 11.
The distance between the school and the house of a student’s house is 1 km 875 m. Every day she walks both ways. Find the total distance covered by her in six days.
Solution :
1 km 875 m = 1 km + 875 m
= 1 × 1000 m + 875 m
= 1000 m + 875 m = 1875 m
Distance covered by her in a day in walking both ways between school and home = 1875 × 2 m = 3750 m
∴ Total distance covered by her in six days in walking both ways between school and home = 3750 m × 6 = 22500 m
= 22000 m + 500 m = \(\frac { 22000 }{ 1000 }\) km + 500 m
= 22 km + 500 m = 22 km 500 m.
Question 12.
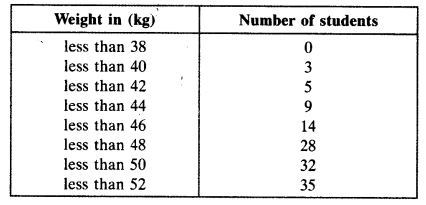
A vessel has 4 liters and 500 ml of curd. In how many glasses, each of 25 ml capacity, can it be filled?
Solution :
41500 ml = 41 + 500 ml
= 4 × 1000 ml + 500 ml
= 4000 ml + 500 ml = 4500 ml
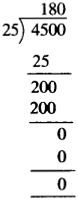
Hence, it can be filled in 180 glasses.
We hope the NCERT Solutions for Class 6 Maths Chapter 1 Knowing Our Numbers Ex 1.2 help you. If you have any query regarding NCERT Solutions for Class 6 Maths Chapter 1 Knowing Our Numbers Ex 1.2, drop a comment below and we will get back to you at the earliest.