NCERT Solutions for Class 8 Maths Chapter 1 Rational Numbers Ex 1.1 are part of NCERT Solutions for Class 8 Maths. Here we have given NCERT Solutions for Class 8 Maths Chapter 1 Rational Numbers Ex 1.1.
| Board | CBSE |
| Textbook | NCERT |
| Class | Class 8 |
| Subject | Maths |
| Chapter | Chapter 1 |
| Chapter Name | Rational Numbers |
| Exercise | Ex 1.1 |
| Number of Questions Solved | 11 |
| Category | NCERT Solutions |
NCERT Solutions for Class 8 Maths will help you to score more marks in your CBSE board Examination.
NCERT Solutions for Class 8 Maths Chapter 1 Rational Numbers Ex 1.1
Question 1.
Using appropriate properties find:
(i) \(-\frac { 2 }{ 5 } \times \frac { 3 }{ 5 } +\frac { 5 }{ 2 } -\frac { 3 }{ 5 } \times \frac { 1 }{ 6 } \)
(ii) \(\frac { 2 }{ 5 } \times \left( -\frac { 3 }{ 7 } \right) -\frac { 1 }{ 6 } \times \frac { 3 }{ 2 } +\frac { 1 }{ 14 } \times \frac { 2 }{ 5 } \)
Solution.
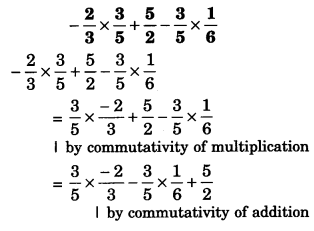
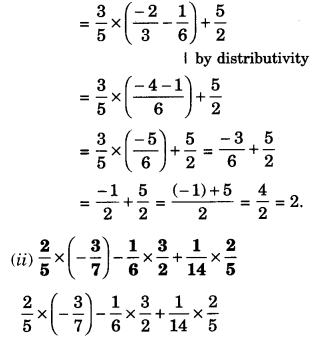

Question 2.
Write the additive inverse of each of the following:
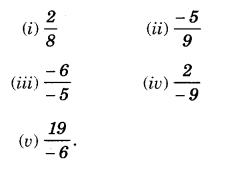
Solution.
(i) \(\frac { 2 }{ 8 } \)
Additive inverse of \(\frac { 2 }{ 8 } \) is \(\frac { 2 }{ 8 } \)
(ii) \(-\frac { 5 }{ 9 } \)
\(\frac { -6 }{ -5 } =\frac { 6 }{ 5 } \)
Additive inverse of \(\frac { -6 }{ -5 } \) is \(\frac { -6 }{ 5 } \)
(iii) \(\frac { -6 }{ -5 } \)
\(\frac { -6 }{ -5 } \)=\(\frac { 6 }{ 5 } \)
Additive inverse of \(\frac { -6 }{ -5 } \) is \(\frac { -6 }{ 5 } \)
(iv) \(\frac { 2 }{ -9 } \)
Additive inverse of \(\frac { 2 }{ -9 } \) is \(\frac { 2 }{ 9 }\)
(v) \(\frac { 19 }{ -6 } \)
Additive inverse of \(\frac { 19 }{ -6 } \) is \(\frac { 19 }{ 6 }\)
Question 3.
Verify that – (-x) = x for :
(i) \(x=\frac { 11 }{ 15 } \)
(ii) \(x=-\frac { 13 }{ 17 } \)
Solution.
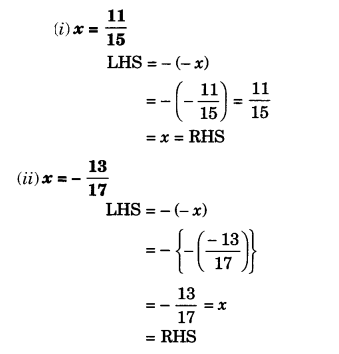
Question 4.
Find the multiplicative inverse of the following:
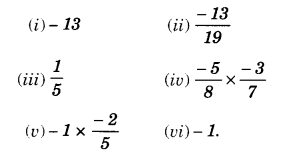
Solution.

Question 5.
Name the property under multiplication used in each of the following:
(i) \(\frac { -4 }{ 5 } \times \left( 1 \right) =1\times \frac { -4 }{ 5 } =-\frac { 4 }{ 5 } \)
(ii) \(-\frac { 13 }{ 17 } \times \frac { -2 }{ 7 } =\frac { -2 }{ 7 } \times \frac { -13 }{ 17 } \)
(iii) \(\frac { -19 }{ 29 } \times \frac { 29 }{ -19 } =1\)
Solution.
(i) 1 is the multiplicative identity
(ii) Commutativity of multiplication
(iii) Multiplicative inverse.
Question 6.
Multiply \(\frac { 6 }{ 13 } \) by the reciprocal of \(\frac { -7 }{ 16 } \)
Solution.
Reciprocal of \(\frac { -7 }{ 16 } \) is \(\frac { -16 }{ 7 } \)
Now,
\(\frac { 6 }{ 13 } \times \frac { -16 }{ 7 } =\frac { 6\times \left( -16 \right) }{ 13\times 7 } =\frac { -96 }{ 91 } \)
Question 7.
Tell what property allows you to compute : \(\frac { 1 }{ 3 } \times \left( 6\times \frac { 4 }{ 3 } \right) \) as \(\left( \frac { 1 }{ 3 } \times 6 \right) \times \frac { 4 }{ 3 } \)
Solution.
Associativity.
Question 8.
Is the \(\frac { 8 }{ 9 } \) multiplicative inverse of \(-1\frac { 1 }{ 8 } \) ? Why or why not?
Solution.
\(-1\frac { 1 }{ 8 } =-\frac { 9 }{ 8 } \)
Now, \(\frac { 8 }{ 9 } \times \frac { -9 }{ 8 } =-1\neq 1\)
So, No ; \(\frac { 8 }{ 9 } \) is not the multiplicative inverse of \(-1\frac { 1 }{ 8 } \left( =-\frac { 9 }{ 8 } \right) \) because the product of \(\frac { 8 }{ 9 } \) and -13(-) and \(-1\frac { 1 }{ 8 } \left( =-\frac { 9 }{ 8 } \right) \) is not 1.
Question 9.
Is 0.3 the multiplicative inverse of \(3\frac { 1 }{ 3 }\) ? Why or why not?
Solution.
Yes ; 0.3 is the multiplicative inverse of \(\frac { 10 }{ 3 } \) because
\(\frac { 3 }{ 10 } \times \frac { 10 }{ 3 } =\frac { 3\times 10 }{ 10\times 3 } =\frac { 30 }{ 30 } =1\)
Question 10.
Write :
(i) The rational number that does not have a reciprocal.
(ii) The rational numbers that are equal to their reciprocals.
(iii) The rational number that is equal to its negative.
Solution.
(i) The rational number ‘0′ does not have a reciprocal.
(ii) The rational numbers 1 and (-1) are equal to their own reciprocals.
(iii) The rational number 0 is equal to its negative.
Question 11.
Fill in the blanks :
(i) Zero has……….reciprocal.
(ii) The numbers……….and………are their own reciprocals.
(iii) The reciprocal of – 5 is.………….
(iv) Reciprocal of \(\frac { 1 }{ x } \), where \(x\neq 0\)
(v) The product of two rational numbers is always a.………
(vi) The reciprocal of a positive rational number is……….
Solution.
(i) Zero has no reciprocal.
(ii) The numbers 1 and -1 are their own reciprocals.
(iii) The reciprocal of – 5 is \(-\frac { 1 }{ 5 } \)
(iv) Reciprocal of \(\frac { 1 }{ x } \), where \(x\neq 0\) is x.
(v) The product of two rational numbers is always a rational number.
(vi) The reciprocal of a positive rational number is positive.
We hope the NCERT Solutions for Class 8 Maths Chapter 1 Rational Numbers Ex 1.1 help you. If you have any query regarding NCERT Solutions for Class 8 Maths Chapter 1 Rational Numbers Ex 1.1, drop a comment below and we will get back to you at the earliest.



 Scale:
Scale: