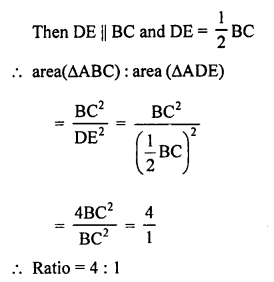
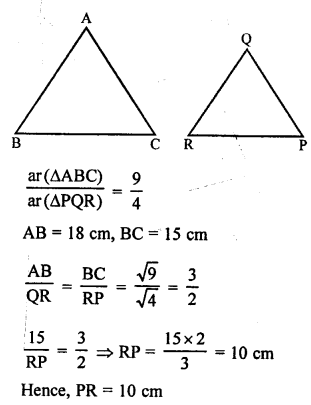
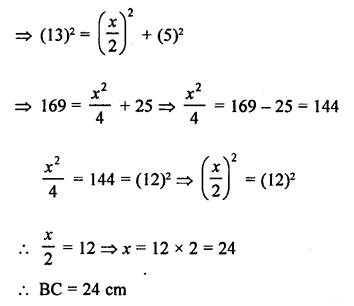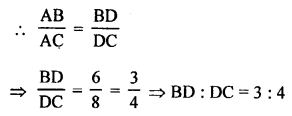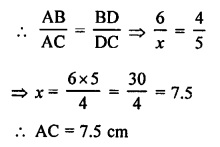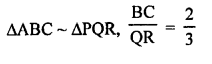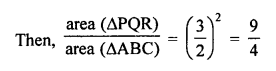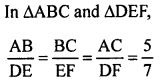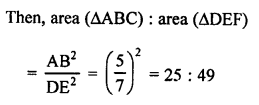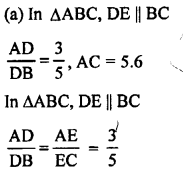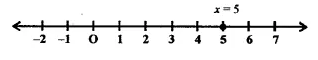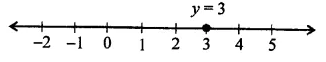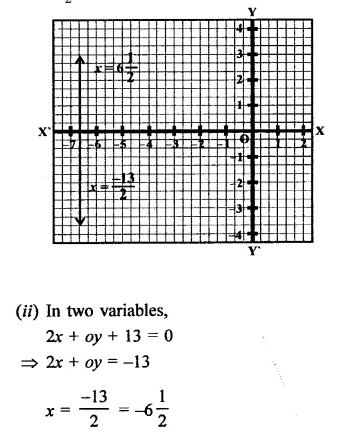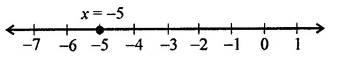RD Sharma Class 9 Solutions Chapter 7 Introduction to Euclid’s Geometry MCQS
These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 7 Introduction to Euclid’s Geometry MCQS
Other Exercises
- RD Sharma Class 9 Solutions Chapter 7 Introduction to Euclid’s Geometry Ex 7.1
- RD Sharma Class 9 Solutions Chapter 7 Introduction to Euclid’s Geometry Ex 7.2
- RD Sharma Class 9 Solutions Chapter 7 Introduction to Euclid’s Geometry Ex 7.3
- RD Sharma Class 9 Solutions Chapter 7 Introduction to Euclid’s Geometry Ex 7.4
- RD Sharma Class 9 Solutions Chapter 7 Introduction to Euclid’s Geometry VSAQS
- RD Sharma Class 9 Solutions Chapter 7 Introduction to Euclid’s Geometry MCQS
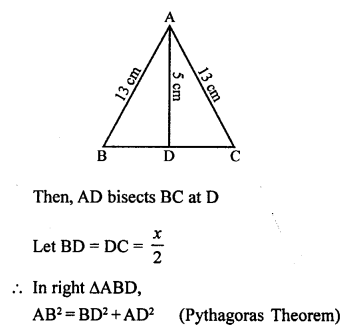
Mark the correct alternative in each of the following:
Question 1.
If (4, 19) is a solution of the equation y = ax + 3, then a =
(a) 3
(b) 4
(c) 5
(d) 6
Solution:
∵ (4, 19) is a solution of equation
y = ax + 3
∴ x = 4, y= 19 will satisfy the equation
∴ 19 = a x 4 + 3 = 4a + 3
4a = 19-3 = 16 ⇒ a= \(\frac { 16 }{ 4 }\) = 4
∴ a = 4 (b)
Question 2.
If (a, 4) lies on the graph of 3x + y = 10, then the value of a is
(a) 3
(b) 1
(c) 2
(d) 4
Solution:
∵ (a, 4) is the solution of the equation 3x + y = 10
∴ x = a, y = 4 will satisfy the equation
∴ Substituting the value of x and y in the equation
3 xa + 4= 10 ⇒ 3a =10- 4 = 6
⇒ a = \(\frac { 6 }{ 3 }\) = 2
∴ a = 2 (c)
Question 3.
The graph of the linear equation 2x – y= 4 cuts x-axis at
(a) (2, 0)
(b) (-2, 0)
(c) (0, -4)
(d) (0, 4)
Solution:
∵ graph of the equation,
2x – y = 4 cuts x-axis
∴ y = 0
∴ 2x – 0 = 4 ⇒ 2x = 4
⇒ x = \(\frac { 4 }{ 2 }\) = 2
∴ The line cuts x-axis at (2, 0) (a)
Question 4.
How many linear equations are satisfied by x = 2 and y = -3 ?
(a) Only one
(b) Two
(c) Three
(d) Infinitely many
Solution:
∵ From a point, infinitely number of lines can pass.
∴ The solution x = 2, y = -3 is the solution of infinitely many linear equations. (d)
Question 5.
The equation x – 2 = 0 on number line is represented by
(a) aline
(b) a point
(c) infinitely many lines
(d) two lines
Solution:
The equation x – 2 = 0
⇒ x = 2
∴ It is representing by a point on a number line. (b)
Question 6.
x = 2, y = -1 is a solution of the linear equation
(a) x + 2y = 0
(b) x + 2y = 4
(c) 2x + y = 0
(d) 2x + y = 5
Solution:
x = 2, y = -1
Substituting the values of x and y in the equations one by one, we get (a) x + 2y = 0
⇒ 2 + 2(-1) = 0
⇒ 2 – 2 = 0
⇒ 0 = 0 which is true (a)
Question 7.
If (2k – 1, k) is a solution of the equation 10x – 9y = 12, then k =
(a) 1
(b) 2
(c) 3
(d) 4
Solution:
∵ (2k – 1, k) is a solution of the equation 10x – 9y = 12
Substituting the value of x and y in the equation
10(2k – 1) – 9k = 12
⇒ 20k – 10-9k= 12
⇒ 20k – 9k = 12 + 10
⇒ 11k = 22
⇒ k =\(\frac { 22 }{ 11 }\) = 2
∴ k = 2 (b)
Question 8.
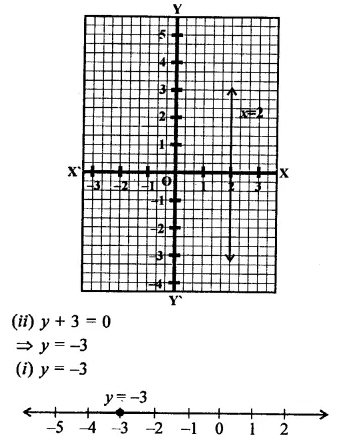
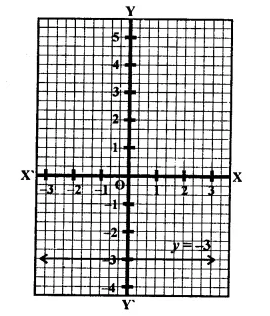
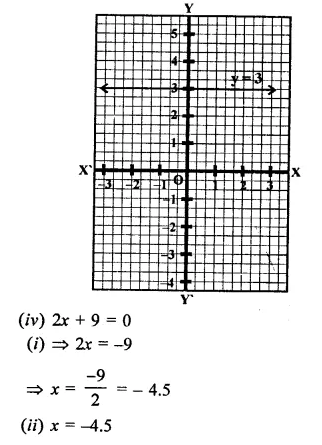
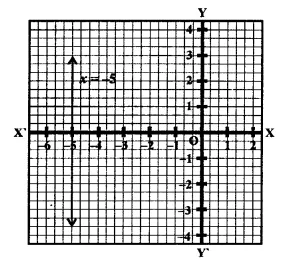
The distance between the graph of the equation x = – 3 and x = 2 is
(a) 1
(b) 2
(c) 3
(d) 5
Solution:
The distance between the graphs of the equation
x = -3 and x = 2 will be
2(-3) = 2+ 3 = 5 (b)
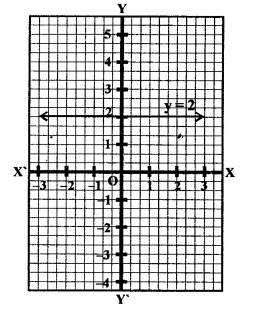
Question 9.
The distance between the graphs of the equations y = -1 and y = 3 is
(a) 2
(b) 4
(c) 3
(d) 1
Solution:
The distance between the graphs of the equation
y = -1 and y = 3
is 3 – (-1) = 3 + 1 = 4 (b)
Question 10.
If the graph of the equation 4x + 3y = 12 cuts the co-ordinate axes at A and B, then hypotenuse of right triangle AOB is of length
(a) 4 units
(b) 3 units
(c) 5 units
(d) none of these
Solution:
Equation is 4x + 3y = 12
If it cuts the x-axis, then y = 0
∴ 4x x 3 x 0 = 12
⇒ 4x = 12 ⇒ x = \(\frac { 12 }{ 4 }\) = 3
OA = 3 units
∴ The point of intersection of x-axis is (3, 0)
Again if it cuts the y-axis, then x = 0 , Y= 0
∴ 4x x 3 x 0 = 12
⇒ 4x = 12 ⇒ x = \(\frac { 12 }{ 3 }\) = 4
⇒ OB = 4 units
∴ The point of intersection is (0, 4)
∴ In right ΔAOB,
AB2 = AO2 + OB2
= (3)2 + (4)2
= 9 + 16 = 25
= (5)2
∴ AB = 5 units (c)
Hope given RD Sharma Class 9 Solutions Chapter 7 Introduction to Euclid’s Geometry MCQS are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.