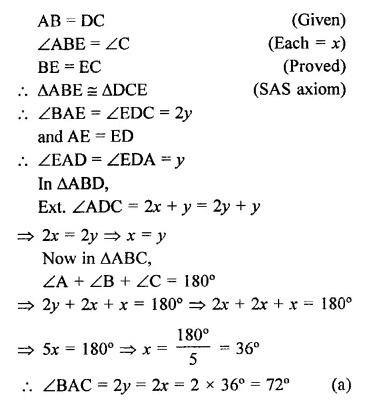Prasanna

RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula MCQS

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula MCQS

Other Exercises

• RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula Ex 12.1
• RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula Ex 12.2
• RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula Ex 12.3
• RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula Ex 12.4
• RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula Ex 12.5
• RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula Ex 12.6
• RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula VSAQS
• RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula MCQS

Mark the correct alternative in each of the following:
Question 1.
In ∆ABC ≅ ∆LKM, then side of ∆LKM equal to side AC of ∆ABC is
(a) LX
(b) KM
(c) LM
(d) None of these
Solution:
Side AC of ∆ABC = LM of ∆LKM (c)

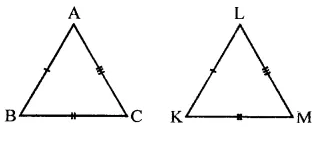
Question 2.
In ∆ABC ≅ ∆ACB, then ∆ABC is isosceles with
(a) AB=AC
(b) AB = BC
(c) AC = BC
(d) None of these
Solution:
∵ ∆ABC ≅ ∆ACB
∴ AB = AC (a)

Question 3.
In ∆ABC ≅ ∆PQR, then ∆ABC is congruent to ∆RPQ, then which of the following is not true:
(a) BC = PQ
(b) AC = PR
(c) AB = PQ
(d) QR = BC
Solution:
∵ ∆ABC = ∆PQR
∴ AB = PQ, BC = QR and AC = PR
∴ BC = PQ is not true (a)

Question 4.
In triangles ABC and PQR three equality relations between some parts are as follows: AB = QP, ∠B = ∠P and BC = PR State which of the congruence conditions applies:
(a) SAS
(b) ASA
(c) SSS
(d) RHS
Solution:
In two triangles ∆ABC and ∆PQR,
AB = QP, ∠B = ∠P and BC = PR
The condition apply : SAS (a)

Question 5.
In triangles ABC and PQR, if ∠A = ∠R, ∠B = ∠P and AB = RP, then which one of the following congruence conditions applies:
(a) SAS
(b) ASA
(c) SSS
(d) RHS
Solution:
In ∆ABC and ∆PQR,
∠A = ∠R
∠B = ∠P
AB = RP
∴ ∆ABC ≅ ∆PQR (ASA axiom) (b)

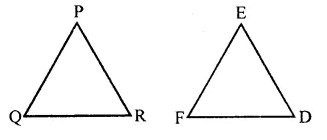
Question 6.
If ∆PQR ≅ ∆EFD, then ED =
(a) PQ
(b) QR
(c) PR
(d) None of these
Solution:
∵ ∆PQR = ∆EFD
∴ ED = PR (c)

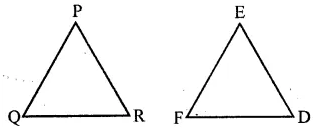
Question 7.
If ∆PQR ≅ ∆EFD, then ∠E =
(a) ∠P
(b) ∠Q
(c) ∠R
(d) None of these
Solution:
∵ ∆PQR ≅ ∆EFD
∴ ∠E = ∠P (a)

Question 8.
In a ∆ABC, if AB = AC and BC is produced to D such that ∠ACD = 100°, then ∠A =
(a) 20°
(b) 40°
(c) 60°
(d) 80°
Solution:
In ∆ABC, AB = AC
∴ ∠B = ∠C
But Ext. ∠ACD = ∠A + ∠B

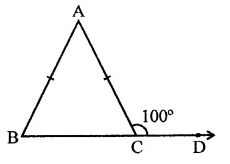
∠ACB + ∠ACD = 180° (Linear pair)
∴ ∠ACB + 100° = 180°
⇒ ∠ACB = 180°-100° = 80°
∴ ∠B = ∠ACD = 80°
But ∠A + ∠B 4- ∠C = 180°
∴ ∠A + 80° + 80° = 180°
⇒∠A+ 160°= 180°
∴ ∠A= 180°- 160° = 20° (a)

Question 9.
In an isosceles triangle, if the vertex angle is twice the sum of the base angles, then the measure of vertex angle of the triangle is
(a) 100°
(b) 120°
(c) 110°
(d) 130°
Solution:
In ∆ABC,
∠A = 2(∠B + ∠C)
= 2∠B + 2∠C

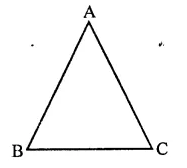
Adding 2∠A to both sides,
∠A + 2∠A = 2∠A + 2∠B + 2∠C
⇒ 3∠A = 2(∠A + ∠B + ∠C)
⇒ 3∠A = 2 x 180° (∵∠A + ∠B + ∠C = 180° )
⇒ 3∠A = 360°
⇒∠A = \(\frac { { 360 }^{ \circ } }{ 3 }\)  = 120°
∴ ∠A = 120° (b)

Question 10.
Which of the following is not a criterion for congruence of triangles?
(a) SAS
(b) SSA
(c) ASA
(d) SSS
Solution:
SSA is not the criterion of congruence of triangles. (b)

Question 11.
In the figure, the measure of ∠B’A’C’ is
(a) 50°
(b) 60°
(c) 70°
(d) 80°

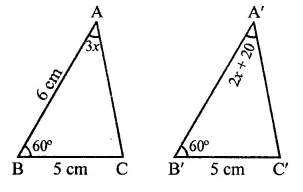
Solution:
In the figure,
∆ABC ≅ ∆A’B’C’
∴ ∠A = ∠A
⇒3x = 2x- + 20
⇒ 3x – 2x = 20
⇒ x = 20
∠B’A’C’ = 2x + 20 = 2 x 20 + 20
= 40 + 20 = 60° (b)

Question 12.
If ABC and DEF are two triangles such that ∆ABC ≅ ∆FDE and AB = 5 cm, ∠B = 40° and ∠A = 80°. Then, which of the following is true?
(a) DF = 5 cm, ∠F = 60°
(b) DE = 5 cm, ∠E = 60°
(c) DF = 5 cm, ∠E = 60°
(d) DE = 5 cm, ∠D = 40°
Solution:
∵ ∆ABC ≅ ∆FDE,
AB = 5 cm, ∠A = 80°, ∠B = 40°
∴ DF = 5 cm, ∠F = 80°, ∠D = 40°
∴ ∠C =180°- (80° + 40°) = 180° – 120° = 60°

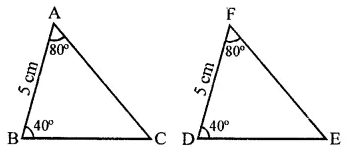
∴ ∠E = ∠C = 60°
∴ DF = 5 cm, ∠E = 60° (c)

Question 13.
In the figure, AB ⊥ BE and FE ⊥ BE. If BC = DE and AB = EF, then ∆ABD is congruent to
(a) ∆EFC
(b) ∆ECF
(c) ∆CEF
(d) ∆FEC

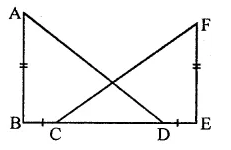
Solution:
In the figure, AB ⊥ BE, FE ⊥ BE
BC = DE, AB = EF,
then CD + BC = CD + DE BD = CE
In ∆ABD and ∆CEF,
BD = CE (Prove)
AB = FE (Given)
∠B = ∠E (Each 90°)
∴ ∆ABD ≅ ∆FCE (b)

Question 14.
In the figure, if AE || DC and AB = AC, the value of ∠ABD is
(a) 70°
(b) 110°
(c) 120°
(d) 130°

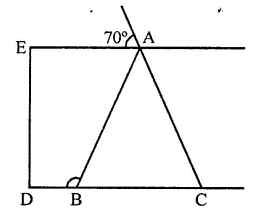
Solution:
In the figure, AE || DC
∴ ∠1 = 70° (Vertically opposite angles)
∴ ∠1 = ∠2 (Alternate angles)
∠2 = ∠ABC (Base angles of isosceles triangle)

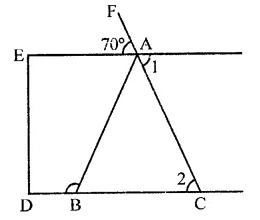
∴ ABC = 90°
But ∠ABC + ∠ABD = 180° (Linear pair)
⇒ 70° +∠ABD = 180°
⇒∠ABD = 180°-70°= 110°
∴ ∠ABD =110° (b)

Question 15.
In the figure, ABC is an isosceles triangle whose side AC is produced to E. Through C, CD is drawn parallel to BA. The value of x is
(a) 52°
(b) 76°
(c) 156°
(d) 104°

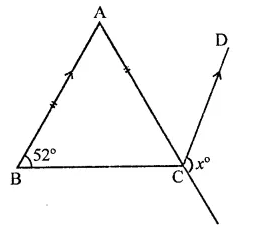
Solution:
In ∆ABC, AB = AC
AC is produced to E

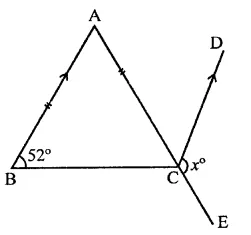
CD || BA is drawn
∠ABC = 52°
∴ ∠ACB = 52° (∵ AB = AC)
∴ ∠BAC = 180°-(52° +52°)
= 180°-104° = 76°
∵ AB || CD
∴ ∠ACD = ∠BAC (Alternate angles)
= 76°
and ∠BCE + ∠DCB = 180° (Linear pair)
∠BCE + 52° = 180°
⇒∠BCE = 180°-52°= 128°
∠x + ∠ACD = 380°
⇒ x + 76° = 180°
∴ x= 180°-76°= 104° (d)

Question 16.
In the figure, if AC is bisector of ∠BAD such that AB = 3 cm and AC = 5 cm, then CD =
(a) 2 cm
(b) 3 cm
(c) 4 cm
(d) 5 cm

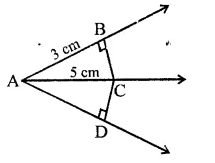
Solution:
In the figure, AC is the bisector of ∠BAD, AB = 3 cm, AC = 5 cm

In ∆ABC and ∆ADC,
AC = AC (Common)
∠B = ∠D (Each 90°)
∠BAC = ∠DAC (∵ AC is the bisector of ∠A)
∴ ∆ABC ≅ ∆ADC (AAS axiom)
∴ BC = CD and AB = AD (c.p.c.t.)
Now in right ∆ABC,
AC² = AB² + BC²
⇒ (5)² = (3)² + BC²
⇒25 = 9 + BC²
⇒ BC² = 25 – 9 = 16 = (4)²
∴ BC = 4 cm
But CD = BC
∴ CD = 4 cm (c)

Question 17.
D, E, F are the mid-point of the sides BC, CA and AB respectively of ∆ABC. Then ∆DEF is congruent to triangle
(a) ABC
(b) AEF
(c) BFD, CDE
(d) AFE, BFD, CDE
Solution:
In ∆ABC, D, E, F are the mid-points of the sides BC, CA, AB respectively
DE, EF and FD are joined

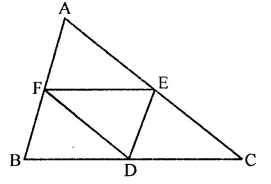
∵ E and F are the mid-points
AC and AB,
∴ EF = \(\frac { 1 }{ 2 }\) BC and EF || BC
Similarly,
DE = \(\frac { 1 }{ 2 }\) AB and DE || AB
DF = \(\frac { 1 }{ 2 }\) AC and DF || AC
∴ ∆DEF is congruent to each of the triangles so formed
∴ ∆DEF is congruent to triangle AFE, BFD, CDE (d)

Question 18.
ABC is an isosceles triangle such that AB = AC and AD is the median to base BC. Then, ∠BAD =
(a) 55°
(b) 70°
(c) 35°
(d) 110°

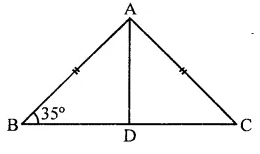
Solution:
In ∆ABC, AB = AC
AD is median to BC

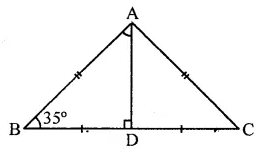
∴ BD = DC
In ∆ADB, ∠D = 90°, ∠B = 35°
But ∠B + BAD + ∠D = 180° (Sum of angles of a triangle)
⇒ 35° + ∠BAD + 90° = 180°
⇒∠BAD + 125°= 180°
⇒ ∠BAD = 180°- 125°
⇒∠BAD = 55° (a)

Question 19.
In the figure, X is a point in the interior of square ABCD. AXYZ is also a square. If DY = 3 cm and AZ = 2 cm, then BY =
(a) 5 cm
(b) 6 cm
(c) 7 cm
(d) 8 cm

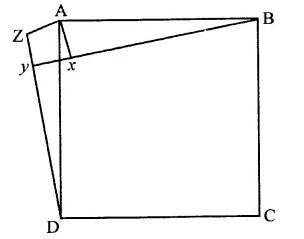
Solution:
In the figure, ABCD and AXYZ are squares
DY = 3 cm, AZ = 2 cm

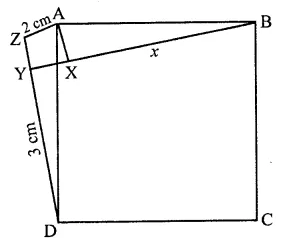
DZ = DY + YZ
= DY + Z = 3 + 2 = 5 cm
In ∆ADZ, ∠2 = 90°
AD² + AZ² + DZ² = 2² + 5² cm
= 4 + 25 = 29
In ∠ABX, ∠X = 90°
AB² = AX² + BX²
AD² = AZ² + BX²
(∵ AB = AD, AX = AZ sides of square)
29 = 2² + BX²
⇒ 29 = 4 + BX²
⇒ BX² = 29 – 4 = 25 = (5)²
∴ BX = 5 cm (a)

Question 20.
In the figure, ABC is a triangle in which ∠B = 2∠C. D is a point on side BC such that AD bisects ∠BAC and AB = CD. BE is the bisector of ∠B. The measure of ∠BAC is
(a) 72°
(b) 73°
(c) 74°
(d) 95°

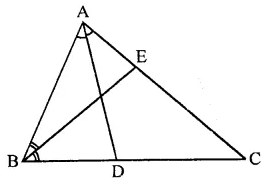
Solution:
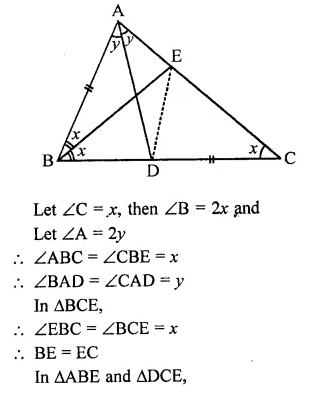
In the figure, ∠B = 2∠C, AD and BE are the bisectors of ∠A and ∠B respectively,
AB = CD

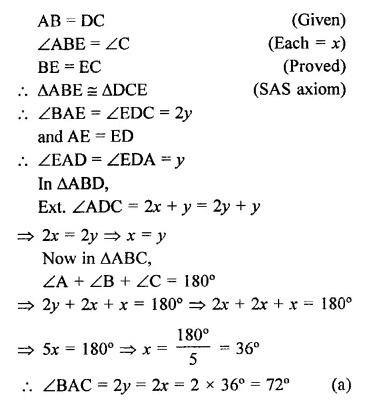
Hope given RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula MCQS are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula VSAQS

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula VSAQS

Other Exercises

• RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula Ex 12.1
• RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula Ex 12.2
• RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula Ex 12.3
• RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula Ex 12.4
• RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula Ex 12.5
• RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula Ex 12.6
• RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula VSAQS
• RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula MCQS

Question 1.
Solution:
In two congruent triangles ABC and DEF, if AB = DE and BC = EF. Name the pairs of equal angles.

In AABC and ADEF,
∆ABC ≅ ∆DEF
and AB = DE, BC = EF
∴ ∠A = ∠D, ∠B = ∠E and ∠C = ∠F

Question 2.
Solution:
In two triangles ABC and DEF, it is given that ∠A = ∠D, ∠B = ∠E and ∠C = ∠F. Are the two triangles necessarily congruent?

No, as the triangles are equiangular, so similar.

Question 3.
Solution:
If ABC and DEF are two triangles such that AC = 2.5 cm, BC = 5 cm, ∠C = 75°, DE = 2.5 cm, DF = 5 cm and ∠D = 75°. Are two triangles congruent?
Yes, triangles are congruent (SAS axiom)

Question 4.
Solution:
In two triangles ABC and ADC, if AB = AD and BC = CD. Are they congruent?
Yes, these are congruent
In two triangles ABC are ADC,
AB = AD (Given)
BC = CD (Given)
and AC = AC (Common)
∴ ∆sABC ≅ AADC (SSS axiom)

Question 5.
Solution:
In triangles ABC and CDE, if AC = CE, BC = CD, ∠A = 60°, ∠C – 30° and ∠D = 90°. Are two triangles congruent?
Yes, triangles are congruent because,
In ∆ABC, and ∆CDE,
AC = CE
BC = CD ∠C = 30°
∴ ∆ABC ≅ ∆CDE (SAS axiom)

Question 6.
Solution:
ABC is an isosceles triangle in which AB = AC. BE and CF are its two medians. Show that BE = CF.

Given : In ∆ABC, AB = AC
BE and CF are two medians

To prove : BE = CF
Proof: In ∆ABE and ∆ACF.
AB = AC (Given)
∠A = ∠A (Common)
AE = AF (Half of equal sides)
∴ ∆ABE ≅ ∆ACF (SAS axiom)
∴ BE = CF (c.p.c.t.)

Question 7.
Solution:
Find the measure of each angle of an equilateral triangle.

In ∆ABC,
AB = AC = BC

∵ AB = AC
∴ ∠C = ∠B …(i)
(Angles opposite to equal sides)
Similarly,
AC = BC
∴ ∠B = ∠A …(ii)
From (i) and (ii),
∠A = ∠B = ∠C
But ∠A + ∠B + ∠C = 180°
(Sum of angles of a triangle)
∴ ∠A + ∠B + ∠C = \(\frac { { 180 }^{ \circ } }{ 3 }\)  = 60°

Question 8.
Solution:
CDE is an equilateral triangle formed on a side CD of a square ABCD. Show that ∆ADE ≅ ∆BCE.

Given : An equilateral ACDE is formed on the side of square ABCD. AE and BE are joined

To prove : ∆ADE ≅ ∆BCE
Proof : In ∆ADE and ∆BCE,
AD = BC (Sides of a square)
DE = CE (Sides of equilateral triangle)
∠ADE = ∠BCE(Each = 90° + 60° = 150°)
∴ AADE ≅ ABCE (SAS axiom)

Question 9.
Solution:
Prove that the sum of three altitude of a triangle is less than the sum of its sides.

Given : In ∆ABC, AD, BE and CF are the altitude of ∆ABC

To prove : AD + BE + CF < AB + BC + CA
Proof : In right ∆ABD, ∠D = 90°
Then other two angles are acute
∵ ∠B < ∠D
∴ AD < AB …(i)
Similarly, in ∆BEC and ∆ABE we can prove thatBE and CF < CA …(iii)
Adding (i), (ii), (iii)
AD + BE -t CF < AB + BC + CA

Question 10.
Solution:
In the figure, if AB = AC and ∠B = ∠C. Prove that BQ = CP.

Given : In the figure, AB = AC, ∠B = ∠C
To prove : BQ = CP
Proof : In ∆ABQ and ∆ACP
AB = AC (Given)
∠A = ∠A (Common)
∠B = ∠C (Given)
∴ ∆ABQ ≅ ∆ACP (ASA axiom)
∴ BQ = CP (c.p.c.t.)

Hope given RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula VSAQS are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.