RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula Ex 12.3
These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula Ex 12.3
Other Exercises
- RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula Ex 12.1
- RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula Ex 12.2
- RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula Ex 12.3
- RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula Ex 12.4
- RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula Ex 12.5
- RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula Ex 12.6
- RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula VSAQS
- RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula MCQS
Question 1.
In two right triangles one side an acute angle of one are equal to the corresponding side and angle of the other. Prove that the triangles are congruent.
Solution:
Given : In ∆ABC and ∆DEF,
∠B = ∠E = 90°
∠C = ∠F
AB = DE
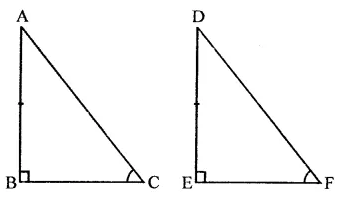
To prove : ∆ABC = ∆DEF
Proof : In ∆ABC and ∆DEF,
∠B = ∠E (Each = 90°)
∠C = ∠F (Given)
AB = DE (Given)
∆ABC = ∆DEF (AAS axiom)
Question 2.
If the bisector of the exterior vertical angle of a triangle be parallel to the base. Show that the triangle is isosceles.
Solution:
Given : In ∆ABC, AE is the bisector of vertical exterior ∠A and AE \(\parallel\) BC
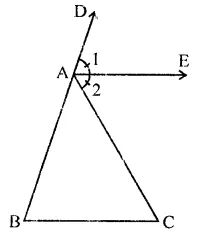
To prove : ∆ABC is an isosceles
Proof: ∵ AE \(\parallel\) BC
∴ ∠1 = ∠B (Corresponding angles)
∠2 = ∠C (Alternate angle)
But ∠1 = ∠2 (∵ AE is the bisector of ∠CAD)
∴ ∠B = ∠C
∴ AB = AC (Sides opposite to equal angles)
∴ ∆ABC is an isosceles triangle
Question 3.
In an isosceles triangle, if the vertex angle is twice the sum of the base angles, calculate the angles of the triangle.
Solution:
Given : In ∆ABC, AB = AC
∠A = 2(∠B + ∠C)
To calculate: Base angles,
Let ∠B = ∠C = x
Then ∠A = 2(∠B + ∠C)
= 2(x + x) = 2 x 2x = 4x
∵ Sum of angles of a triangle = 180°
∴ 4x + x + x – 180° ⇒ 6x = 180°
⇒ x= \(\frac { { 180 }^{ \circ } }{ 6 }\) = 30° o
∴ ∠B = ∠C = 30 and ∠A = 4 x 30° = 120
Question 4.
Prove that each angle of an equilateral triangle is 60°. [NCERT]
Solution:
Given : ∆ABC is an equilateral triangle
Proof: In ∆ABC,
AB = AC (Sides of an equilateral triangle)
∴ ∠C = ∠B …(i)
(Angles opposite to equal angles)
Similarly, AB = BC
∴ ∠C = ∠A …(ii)
From (i) and (ii),
∠A = ∠B = ∠C
But ∠A + ∠B + ∠C = 180° (Sum of angles of a triangle)
∴ ∠A = ∠B = ∠C = \(\frac { { 180 }^{ \circ } }{ 3 }\)= 60°
Question 5.
Angles A, B, C of a triangle ABC are equal to each other. Prove that ∆ABC is equilateral.
Solution:
Given : In ∆ABC, ∠A = ∠B = ∠C
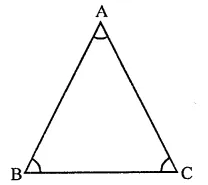
To prove : ∆ABC is an equilateral
Proof: In ∆ABC,
∴ ∠B = ∠C (Given)
∴ AC = AB …(i) (Sides opposite to equal angles)
Similarly, ∠C = ∠A
∴ BC =AB …(ii)
From (i) and (ii)
AB = BC = CA
Hence ∆ABC is an equilateral triangle
Question 6.
ABC is a right angled triangle in which ∠A = 90° and AB = AC. Find ∠B and ∠C.
Solution:
In ∆ABC, ∠A = 90°
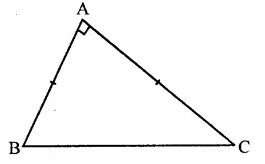
AB =AC (Given)
∴ ∠C = ∠B (Angles opposite to equal sides)
But ∠B + ∠C = 90° (∵ ∠B = 90°)
∴ ∠B = ∠C = \(\frac { { 90 }^{ \circ } }{ 2 }\) = 45°
Hence ∠B = ∠C = 45°
Question 7.
PQR is a triangle in which PQ = PR and S is any point on the side PQ. Through S, a line is drawn parallel to QR and intersecting PR at T. Prove that PS = PT.
Solution:
Given : In ∆PQR, PQ = PR
S is a point on PQ and PT || QR
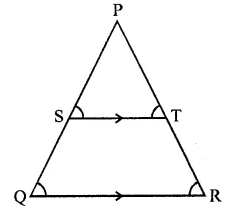
To prove : PS = PT
Proof : ∵ST || QR
∴ ∠S = ∠Q and ∠T = ∠R (Corresponding angles)
But ∠Q = ∠R (∵ PQ = PR)
∴ PS = PT (Sides opposite to equal angles)
Question 8.
In a ∆ABC, it is given that AB = AC and the bisectors of ∠B and ∠C intersect at O. If M is a point on BO produced, prove that ∠MOC = ∠ABC.
Solution:
Given : In ∆ABC, AB = AC the bisectors of ∠B and ∠C intersect at O. M is any point on BO produced.
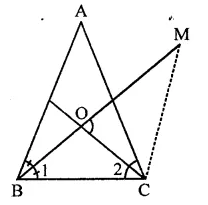
To prove : ∠MOC = ∠ABC
Proof: In ∆ABC, AB = BC
∴ ∠C = ∠B
∵ OB and OC are the bisectors of ∠B and ∠C
∴ ∠1 =∠2 = \(\frac { 1 }{ 2 }\)∠B
Now in ∠OBC,
Ext. ∠MOC = Interior opposite angles ∠1 + ∠2
= ∠1 + ∠1 = 2∠1 = ∠B
Hence ∠MOC = ∠ABC
Question 9.
P is a point on the bisector of an angle ∠ABC. If the line through P parallel to AB meets BC at Q, prove that triangle BPQ is isosceles.
Solution:
Given : In ∆ABC, P is a point on the bisector of ∠B and from P, RPQ || AB is draw which meets BC in Q
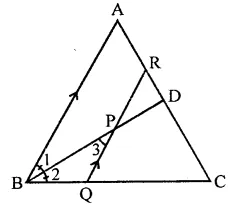
To prove : ∆BPQ is an isosceles
Proof : ∵ BD is the bisectors of CB
∴ ∠1 = ∠2
∵ RPQ || AB
∴ ∠1 = ∠3 (Alternate angles)
But ∠1 == ∠2 (Proved)
∴ ∠2 = ∠3
∴ PQ = BQ (sides opposite to equal angles)
∴ ∆BPQ is an isosceles
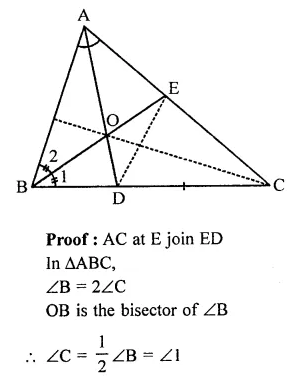
Question 10.
ABC is a triangle in which ∠B = 2∠C, D is a point on BC such that AD bisects ∠BAC = 72°.
Solution:
Given: In ∆ABC,
∠B = 2∠C, AD is the bisector of ∠BAC AB = CD
To prove : ∠BAC = 72°
Construction : Draw bisector of ∠B which meets AD at O

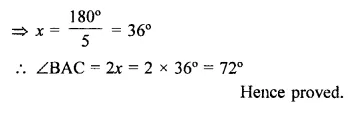
Hope given RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula Ex 12.3 are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.