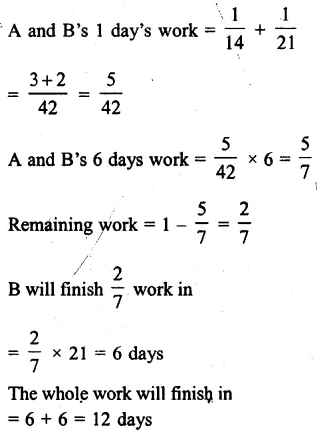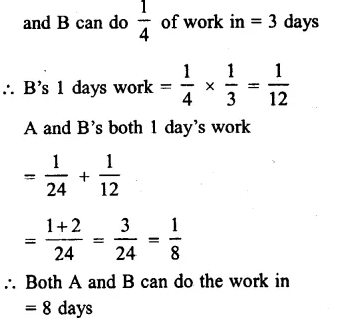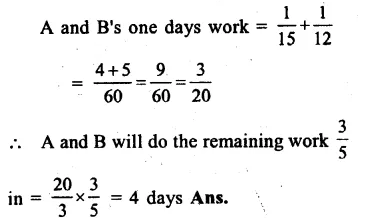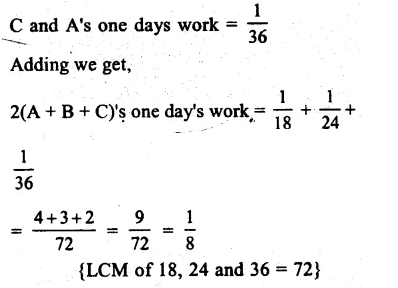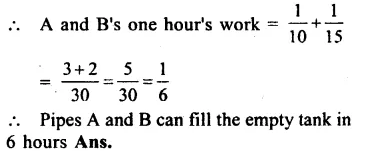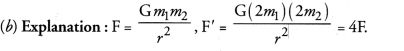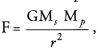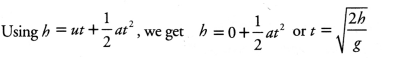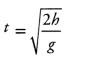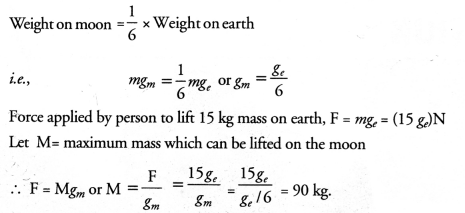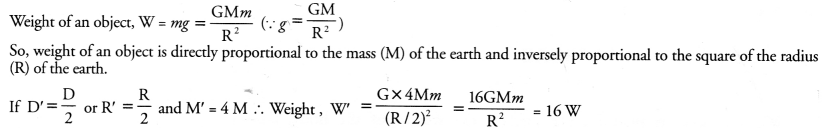Prasanna – Page 961 – MCQ Questions

RS Aggarwal Class 8 Solutions Chapter 13 Time and Work Ex 13A

January 5, 2022July 5, 2018 by Prasanna

RS Aggarwal Class 8 Solutions Chapter 13 Time and Work Ex 13A

These Solutions are part of RS Aggarwal Solutions Class 8. Here we have given RS Aggarwal Solutions Class 8 Chapter 13 Time and Work Ex 13A.

Other Exercises

Question 1.
Solution:
Rajan’s one day’s work = \(\\ \frac { 1 }{ 24 } \)
Amit’s one day’s work = \(\\ \frac { 1 }{ 30 } \)
RS Aggarwal Class 8 Solutions Chapter 13 Time and Work Ex 13A 1.1

Question 2.
Solution:
Ravi’s one hours = \(\\ \frac { 1 }{ 15 } \)
Both’s one day’s work = \(\\ \frac { 1 }{ 12 } \)
RS Aggarwal Class 8 Solutions Chapter 13 Time and Work Ex 13A 2.1
or 6 hours, 40 minutes.

Question 3.
Solution:
A and B both’s one day’s work = \(\\ \frac { 1 }{ 6 } \)
A’s alone’s one day’s work = \(\\ \frac { 1 }{ 9 } \)
RS Aggarwal Class 8 Solutions Chapter 13 Time and Work Ex 13A 3.1

Question 4.
Solution:
Raju and Siraj’s 1 hour work = \(\\ \frac { 1 }{ 6 } \)
Raju’s alone 1 hour work = \(\\ \frac { 1 }{ 15 } \)
RS Aggarwal Class 8 Solutions Chapter 13 Time and Work Ex 13A 4.1

Question 5.
Solution:
A’s one day’s work = \(\\ \frac { 1}{ 10 } \)
B’s one day’s work = \(\\ \frac { 1 }{ 12 } \)
RS Aggarwal Class 8 Solutions Chapter 13 Time and Work Ex 13A 5.1

Question 6.
Solution:
A’s 1 hour work = \(\\ \frac { 1 }{ 24 } \)
B’s 1 hour work = \(\\ \frac { 1 }{ 16 } \)
RS Aggarwal Class 8 Solutions Chapter 13 Time and Work Ex 13A 6.1

Question 7.
Solution:
A,B and C’s 1 hr work = \(\\ \frac { 1 }{ 8 } \)
A’s 1 hour work = \(\\ \frac { 1 }{ 20 } \)
B’s 1 hour work = \(\\ \frac { 1 }{ 24 } \)
RS Aggarwal Class 8 Solutions Chapter 13 Time and Work Ex 13A 7.1

Question 8.
Solution:
A’s one day’s work = \(\\ \frac { 1 }{ 16 } \)
B’s one days work = \(\\ \frac { 1 }{ 12 } \)
RS Aggarwal Class 8 Solutions Chapter 13 Time and Work Ex 13A 8.1

Question 9.
Solution:
A’s 1 day’s work = \(\\ \frac { 1 }{ 14 } \)
B’s 1 day’s work = \(\\ \frac { 1 }{ 21 } \)
RS Aggarwal Class 8 Solutions Chapter 13 Time and Work Ex 13A 9.1

Question 10.
Solution:
A can do \(\\ \frac { 2 }{ 3 } \) work in = 16 days
A’s 1 days work = \(\\ \frac { 2 }{ 3 } \) x \(\\ \frac { 1 }{ 16 } \) = \(\\ \frac { 1 }{ 24 } \)
RS Aggarwal Class 8 Solutions Chapter 13 Time and Work Ex 13A 10.1

Question 11.
Solution:
A’s one day’s work = \(\\ \frac { 1 }{ 15 } \)
B’s one day’s work = \(\\ \frac { 1 }{ 12 } \)
RS Aggarwal Class 8 Solutions Chapter 13 Time and Work Ex 13A 11.1

Question 12.
Solution:
A and B’s one day’s work = \(\\ \frac { 1 }{ 18 } \)
B and C’s one day’s work = \(\\ \frac { 1 }{ 24 } \)
RS Aggarwal Class 8 Solutions Chapter 13 Time and Work Ex 13A 12.1
A, B and C’s one days work = \(\frac { 1 }{ 2\times 2 } \)
= \(\\ \frac { 1 }{ 16 } \)
A, B and C can do the work in 16 days.

Question 13.
Solution:
A and B’s one days work = \(\\ \frac { 1 }{ 12 } \)
B and C’s one day’s work = \(\\ \frac { 1 }{ 15 } \)
RS Aggarwal Class 8 Solutions Chapter 13 Time and Work Ex 13A 13.1

Question 14.
Solution:
A’s one hr work =\(\\ \frac { 1 }{ 10 } \)
B’s one hr work = \(\\ \frac { 1 }{ 15 } \)
RS Aggarwal Class 8 Solutions Chapter 13 Time and Work Ex 13A 14.1

Question 15.
Solution:
Pipe A’s one hour’s work for filling the tank = \(\\ \frac { 1 }{ 5 } \)
Pipe B’s one hour’s work for emptying = \(\\ \frac { 1 }{ 6 } \)
RS Aggarwal Class 8 Solutions Chapter 13 Time and Work Ex 13A 15.1

Question 16.
Solution:
Tap A’s one hour’s work = \(\\ \frac { 1 }{ 6 } \)
Tap B’s one hour’s work = \(\\ \frac { 1 }{ 8 } \)
Tap C’s one hour’s work = \(\\ \frac { 1 }{ 12 } \)
A, B and C’s together one hour’s work
RS Aggarwal Class 8 Solutions Chapter 13 Time and Work Ex 13A 16.1

Question 17.
Solution:
Inlet A’s 1 minutes work = \(\\ \frac { 1 }{ 12 } \)
Inlet B’s 1 minutes work = \(\\ \frac { 1 }{ 15 } \)
RS Aggarwal Class 8 Solutions Chapter 13 Time and Work Ex 13A 17.1

Question 18.
Solution:
The inlet pipe’s 1 hour’s work = \(\\ \frac { 1 }{ 9 } \)
The leak and inlet’s 1 hours work = \(\\ \frac { 1 }{ 10 } \)
Leak’s 1 hour work = \(\frac { 1 }{ 9 } -\frac { 1 }{ 10 } \)
= \(\\ \frac { 10-9 }{ 90 } \)
= \(\\ \frac { 1 }{ 90 } \)
The leak can empty the cistern in = 90 hours Ans.

Question 19.
Solution:
Inlet pipe A’s one hour’s work = \(\\ \frac { 1 }{ 6 } \)
Inlet pipe B’s one hour’s work = \(\\ \frac { 1 }{ 8 } \)
RS Aggarwal Class 8 Solutions Chapter 13 Time and Work Ex 13A 19.1

Hope given RS Aggarwal Solutions Class 8 Chapter 13 Time and Work Ex 13A are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

NCERT Exemplar Solutions for Class 9 Science Chapter 10 Gravitation

January 5, 2022July 5, 2018 by Prasanna

NCERT Exemplar Solutions for Class 9 Science Chapter 10 Gravitation

These Solutions are part of NCERT Exemplar Solutions for Class 9 Science . Here we have given NCERT Exemplar Solutions for Class 9 Science Chapter 10 Gravitation

MULTIPLE CHOICE QUESTIONS

Question 1.
Two objects of different masses falling freely near the surface of moon would
(a) have same velocities at any instant
(b) have different accelerations
(c) experience forces of same magnitude
(d) undergo a change in their inertia.
Answer:
(a) Explanation : During free fall, acceleration remains the same irrespective of the mass of the object. Force is directly proportional to the mass of a freely falling object.

More Resources

Question 2.
The value of acceleration due to gravity
(a) is same on equator and poles
(b) is least on poles
(c) is least on equator
(d) increases from pole to equator.
Answer:
(c) Explanation :

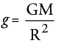
Equatorial radius (R) is more than the polar radius.

Question 3.
The gravitational force between two objects is F. If masses of both objects are halved without changing distance between them, then the gravitation force would become
(a) F/4
(b) F/2
(c) F
(d) 2F
Answer:
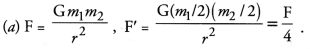
NCERT Exemplar Solutions for Class 9 Science Chapter 10 Gravitation image - 1

Question 4.
A boy is whirling a stone tied with a string in an horizontal circular path the string breaks, the stone
(a) will continue to move in the circular path
(b) will move along a straight line towards the centre of the circular path
(c) will move along a straight line tangential to the circular path
(d) will move along a straight line perpendicular to the circular path away from the boy.
Answer:
(c) Explanation : Due to inertia of directions.

Question 5.
In the relation F = G M m/d², the quantity G
(a) depends on the value of g at the place of observation
(b) is used only when the earth is one of the two masses
(c) is greatest at the surface of the earth
(d) is universal constant of nature.
Answer:
(d) Explanation : The value of ‘G’ is same throughout the universe.

Question 6.
Law of gravitation gives the gravitational force between
(a) the earth and a point mass only
(b) the earth and sun only
(c) any two bodies having some mass
(d) two charged bodies only.
Answer:

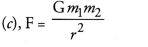
Question 7.
The value of quantity G in the law of gravitation
(a) depends on mass of earth only
(b) depends on radius of earth only
(c) depends on both mass and radius of earth
(d) is independent of mass and radius of the earth.
Answer:
(d) Explanation : G is universal constant.

Question 8.
Two particles are placed at some distance. If the mass of each of the two particles is doubled, keeping the distance between them unchanged, the value of gravitational force between them will be
(a) 1/4 times
(b) 4 times
(c) 1/2 times
(d) unchanged.
Answer:
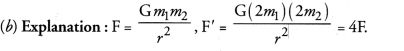
NCERT Exemplar Solutions for Class 9 Science Chapter 10 Gravitation image - 3

Question 9.
The atmosphere is held to the earth by
(a) gravity
(b) wind
(c) clouds
(d) earths magnetic field.
Answer:
(a).

Question 10.
The force of attraction between two unit point masses separated by a unit distance is called
(a) gravitational potential
(b) acceleration due to gravity
(c) gravitational field
(d) universal gravitational constant.
Answer:
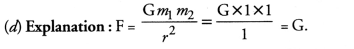
NCERT Exemplar Solutions for Class 9 Science Chapter 10 Gravitation image - 4

Question 11.
The weight of an object at the centre of the earth of radius R is
(a) zero
(b) infinite
(c) R times the weight at the surface of the earth
(d) 1/R² times the weight at surface of the earth.
Answer:
(a) Explanation : W = mg. The value of ‘g’ at the centre of earth is zero.

Question 12.
An apple falls from a tree because of gravitational attraction between the earth and apple. If F₁ is the magnitude of force exerted by the earth on the apple and F₂ is the magnitude of force exerted by apple on earth, then
(a) F₁ is very much greater than F₂
(b) F₂ is very much greater than F₁
(c) F₁ is only a little greater than F₂
(d) F₁ and F₂ are equal.
Answer:

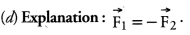
SHORT ANSWER Of QUESTIONS

Question 13.
What is the source of centripetal force that a planet requires to revolve around the sun ? On what factors does that force depend ?
Answer:
The source of centripetal force that a planet requires to revolve around the sun is the gravitational force between the sun and the planet. Thus,
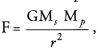
NCERT Exemplar Solutions for Class 9 Science Chapter 10 Gravitation image - 6
where m is the mass of the sun, is the mass of the planet and r is the distance between the sun and the planet.
Thus, the force depends upon

the mass of the sun,
the mass of the planet and
the distance between the sun and the planet.

Question 14.
On the earth, a stone is thrown from a height in a direction parallel to the earths surface while another stone is simultaneously dropped from the same height. Which stone would reach the ground first and why ?
Answer:
Both stones will reach the ground simultaneously. Initial velocity of both the stones in the downward direction is zero and the acceleration of both the stones in the downward direction is same and equal to g.
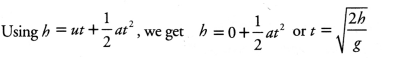
NCERT Exemplar Solutions for Class 9 Science Chapter 10 Gravitation image - 7
so both stones take same time to reach the ground.

Question 15.
Suppose gravity of earth suddenly becomes zero, then in which direction will the moon begin to move if no other celestial body affects it ?
Answer:
Gravity of earth provides necessary centripetal force to the moon to move in a circular path around the earth. If gravity becomes zero, there is no centripetal force and hence, the moon will begin to move in a straight line along to the tangent at the point on the circular path due to inertia of direction.

Question 16.
Identical packets are dropped from two aeroplanes. One above the equator and the other above the north pole both at height h. Assuming all conditions are identical will those packets take same time to reach the surface of earth. Justify your answer.
(CBSE Sample Paper)
Answer:
Time taken by an object to fall through height h at a place is given by
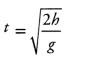
NCERT Exemplar Solutions for Class 9 Science Chapter 10 Gravitation image - 8
Since, value of ‘g’ at poles is greater than at the equator, therefore, packet dropped above the north pole will take less time than the packet dropped above the equator to reach the surface of the earth.

Question 17.
The weight of any person on the moon is about 1/6 times that on the earth. He can lift a mass of 15 kg on the earth. Whatwill be the maximum mass, which can be lifted by the same force applied by the person on the moon ? (CBSE Sample Paper)
Answer:
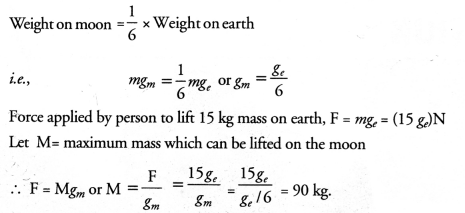
NCERT Exemplar Solutions for Class 9 Science Chapter 10 Gravitation image - 9

Question 18.
Calculate the average density of earth in terms of g, G,m?
Answer:
NCERT Exemplar Solutions for Class 9 Science Chapter 10 Gravitation image - 10

Question 19.
The earth is acted upon by gravitation of sun, even though it does not fall into the sun. Why ? (CBSE 2012)
Answer:
The earth revolves around the sun. The centripetal force is needed by the earth to revolve around the sun. This centripetal force is provided by the gravitational force between the sun and the earth. The earth keeps on moving around the sun as long as gravitational force between the earth and the sun acts on it.

Question 20.
How does the weight of an object vary with respect to mass and radius of the earth. In a hypothetical case, if the diameter of the earth becomes half of its present value and its mass becomes four times of its present value, then how would the weight of any object on the surface of the earth be affected ? (CBSE 2012)
Answer:
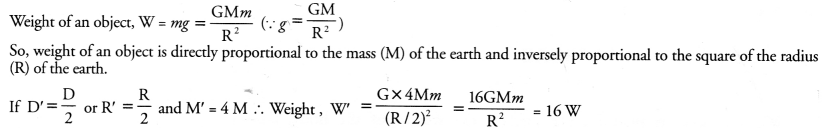
NCERT Exemplar Solutions for Class 9 Science Chapter 10 Gravitation image - 11

Question 21.
How does the force of attraction between two bodies depend upon their masses and distance between them ? A student thought that two bricks tied together would fall faster than a single one under the action of gravity. Do you agree with this hypothesis or not ? Comment.
Answer:
The force of attraction between two bodies of masses m₁ and m₂ and separated by a distance r is given by

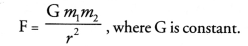
This force is known as gravitational force. The gravitational force is

directly proportional to the product of the masses of two bodies and
inversely proportional to the square of the distance between them.

The hypothesis is not correct. This is because, all bodies in the absence of any force of friction fall with the same acceleration (known as acceleration due to gravity) irrespective of their masses. Hence two bricks tied together will not fall faster than a single brick under the action of gravity.

Question 22.
Two objects of masses m₁ and m₂having the same size are dropped simultaneously from heights h₁ and h₂– respectively. Find out the ratio of time they would take in reaching the ground. Will this ratio remain the same if

one of the object is hollow and the other one is solid and
both of them are hollow, size remaining the same in each case. Give reason.

Answer:
NCERT Exemplar Solutions for Class 9 Science Chapter 10 Gravitation image - 13
Ratio will be same as it does not depend on the mass and size of objects.

Hope given NCERT Exemplar Solutions for Class 9 Science Chapter 10 Gravitation are helpful to complete your science homework.

If you have any doubts, please comment below. Learn Insta try to provide online science tutoring for you.

RS Aggarwal Class 8 Solutions Chapter 12 Direct and Inverse Proportions Ex 12C

January 5, 2022July 5, 2018 by Prasanna

RS Aggarwal Class 8 Solutions Chapter 12 Direct and Inverse Proportions Ex 12C

These Solutions are part of RS Aggarwal Solutions Class 8. Here we have given RS Aggarwal Solutions Class 8 Chapter 12 Direct and Inverse Proportions Ex 12C.

Other Exercises

OBJECTIVE QUESTIONS :
Tick the correct answer in each of the following :

Question 1.
Solution:
Answer = (d)
Cost of 14 kg of pulses = Rs 882
Cost of 1 kg of pulses Rs \(\\ \frac { 882 }{ 14 } \)
Cost of 22 kg of pulses = Rs \(\frac { 882\times 22 }{ 14 } \)
= 63 x 22
= Rs 1386

Question 2.
Solution:
Let x be oranges which can be bought for Rs. 33.80
8 : x : : 10.40 : 33.80
=> x × 10.40 = 8 x 33.80
=> \(\frac { 8\times 33.80 }{ 10.40 } \)
=> \(\frac { 8\times 3380 }{ 1040 } \)
= 26
∴ No. of oranges = 26 Ans. (c)

Question 3.
Solution:
No. of bottles 420 x
Time 3 5
More time, more bottles
By direct proportion
420 : x :: 3 : 5
x = \(\frac { 420\times 5 }{ 3 } \)
= 700
∴ No. of bottle will be 700 (b)

Question 4.
Solution:
Distance covered 75 km x
Time taken 60 min. 20 min.
Less time, less distance By direct proportion,
75 : x :: 60 : 20
x = \(\frac { 75\times 20 }{ 60 } \)
= 25
∴ Distance covered = 25 km (a)

Question 5.
Solution:
No. of sheets 12 : x
Weight 40 g : 1000 g
More weight, more sheets
By direct proportion 12 : x :: 40 : 1000
x = \(\frac { 12\times 1000 }{ 40 } \)
= 300
∴ No. of sheets = 300 (c)

Question 6.
Solution:
Let x be the height of tree
Height of pole 14 m : x m
Length of shadow 10 m : 7 m
Less shadow, less height
By direct proportion 14 : x :: 10 : 7
x = \(\frac { 14\times 7 }{ 10 } \)
= \(\\ \frac { 98 }{ 10 } \)
= 9.8 m
∴ Height of the = 9.8 m (b)

Question 7.
Solution:
Let actual length of bacteria = x cm
Enlarged (times) 50000
Length 5 cm
Then actual length (x)
Then \(\frac { x\times 50000 }{ -4 } \)
= 5
=> x = \(\\ \frac { 5 }{ 50000 } \)
= \(\\ \frac { 1 }{ 10000 } \)
= 10 cm (c)

Question 8.
Solution:
No. of pipes 6 : 5
Time taken to 120 min : x min
fill the tank
Less pipes, more time
By inverse proportion 6 : 5 :: x : 120
x = \(\frac { 6\times 120 }{ 5 } \)
= 144 (b)
∴ Time taken = 144 minutes

Question 9.
Solution:
Let number of days = x, then
Persons 3 : 4
(Time taken to build a wall) 4 : x
More person, less time take
By inverse proportion,
3 : 4 :: x : 4
x = \(\frac { 4\times 3 }{ 4 } \)
= 3 (b)
∴ Time taken to build the wall = 3 days

Question 10.
Solution:
Let time taken will be x hrs
Speed 60 km/h : 80 km/h
Time taken to 2hr : x
reach
(More speed, less time)
By inverse proportion 60 : 80 :: x : 2
x = \(\frac { 60\times 2 }{ 80 } \)
= \(\\ \frac { 3 }{ 2 } \)
∴ Time take \(\\ \frac { 3 }{ 2 } \) hours or 1 hr. 30 m in. (a)

Hope given RS Aggarwal Solutions Class 8 Chapter 12 Direct and Inverse Proportions Ex 12C are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

Value Based Questions in Science for Class 9 Chapter 10 Gravitation

January 5, 2022July 4, 2018 by Prasanna

Value Based Questions in Science for Class 9 Chapter 10 Gravitation

These Solutions are part of Value Based Questions in Science for Class 9. Here we have given Value Based Questions in Science for Class 9 Chapter 10 Gravitation

Question 1.
A spring balance for measuring weight of the range 0-0.5 kg wt has total 10 divisions on its scale. What is the least count of the spring balance ?
Answer:
Least count of the spring balance = Value of 1 division on its scale.
Here, 10 divisions = 0.5 kg wt

Therefore, least count of the spring balance = 0.05 kg wt.

More Resources

Question 2.
A spring balance of the range 0-1 kg wt has total 100 divisions on its scale. What is the least count of the spring balance ?
Answer:
100 divisions = 1 kg wt

Therefore, least count of the spring balance = 0.01 kg wt.

Question 3.
A spring balance of the range 0-2 kg wt has total 100 divisions on its scale. The pointer of the spring balance is in front of 10th division, when an object is suspended with the hook of the spring balance. What is the weight of the object ?
Answer:
100 divisions = 2 kg wt
Value Based Questions in Science for Class 9 Chapter 10 Gravitation image - 3

Hope given Value Based Questions in Science for Class 9 Chapter 10 Gravitation are helpful to complete your science homework.

If you have any doubts, please comment below. Learn Insta try to provide online science tutoring for you.

RD Sharma Class 9 Solutions Chapter 18 Surface Areas and Volume of a Cuboid and Cube Ex 18.1

January 5, 2022July 4, 2018 by Prasanna

RD Sharma Class 9 Solutions Chapter 18 Surface Areas and Volume of a Cuboid and Cube Ex 18.1

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 18 Surface Areas and Volume of a Cuboid and Cube Ex 18.1

Other Exercises

Question 1.
Find the lateral surface area and total surface area of a cuboid of length 80 cm, breadth 40 cm and height 20 cm.
Solution:
Length of cuboid (l) = 80 cm
Breadth (b) = 40 cm
Height (h) = 20 cm
(i) ∴ Lateral surface area = 2h(l + b)
= 2 x 20(80 + 40) cm²
= 40 x 120 = 4800 cm²
(ii) Total surface area = 2(lb + bh + hl)
= 2(80 x 40 + 40 x 20 + 20 x 80) cm²
= 2(3200 + 800 + 1600) cm²
= 5600 x 2 = 11200 cm²

Question 2.
Find the lateral surface area and total surface area of a cube of edge 10 cm.
Solution:
Edge of cube (a) = 10 cm
(i) ∴ Lateral surface area = 4a²
= 4 x (10)² = 4 x 100 cm²= 400 cm²
(ii) Total surface area = 6a² = 6 x(10)² cm²
= 6 x 100 = 600 cm²

Question 3.
Find the ratio of the total surface area and lateral surface area of a cube.
Solution:
Let a be the edge of the cube, then Total surface area = 6a2²
and lateral surface area = 4a²
Now ratio between total surface area and lateral surface area = 6a² : 4a² = 3 : 2

Question 4.
Mary wants to decorate her Christmas tree. She wants to place the tree on a wooden block covered with coloured paper with picture of Santa Claus on it. She must know the exact quantity of paper to buy for this purpose. If the box has length, breadth and height as 80 cm, 40 cm and 20 cm respectively. How many square sheets of paper of side 40 cm would she require? [NCERT]
Solution:
Length of box (l) = 80 cm
Breadth (b) = 40 cm
and height (h) = 20 cm
∴ Total surface area = 2(lb + bh + hl)
= 2[80 x 40 + 40 x 20 + 20 x 80] cm²
= 2[3200 + 800 + 1600] cm² = 2 x 5600 = 11200 cm²
Size of paper sheet = 40 cm
∴ Area of one sheet = (40 cm)² = 1600 cm²
∴ No. of sheets required for the box = 11200 = 1600 = 7 sheets

Question 5.
The length, breadth and height of a room are 5 m, 4 m and 3 m respectively. Find the cost of white washing the walls of the room and the ceiling at the rate of ₹7.50 m².
Solution:
Length of a room (l) = 5m
Breadth (b) = 4 m
and height (h) = 3 m
∴ Area of 4 walls = 2(l + b) x h
= 2(5 + 4) x 3 = 6 x 9 = 54 m²
and area of ceiling = l x b = 5 x 4 = 20 m²
∴ Total area = 54 + 20 = 74 m2
Rate of white washing = 7.50 per m²
∴ Total cost = ₹74 x 7.50 = ₹555

Question 6.
Three equal cubes are placed adjacently in a row. Find the ratio of total surface area of the new cuboid to that of the sum of the surface areas of the three cubes.
Solution:
Let each side of a cube = a cm
Then surface area = 6a² cm²
and surface area of 3 such cubes = 3 x 6a² = 18a² cm²
By placing three cubes side by side we get a cuboid whose,
Length (l) = a x 3 = 3a
Breadth (b) = a
Height (h) = a
∴ Total surface area = 2(lb + bh + hf)
= 2[3a x a+a x a+a x 3a] cm²
= 2[3a² + a² + 3a²] = 14 a²
∴ Ratio between their surface areas = 14a² : 18a² = 7 : 9

Question 7.
A 4 cm cube is cut into 1 cm cubes. Calculate the total surface area of all the small cubes.
Solution:
Side of cube = 4 cm
But cutting into 1 cm cubes, we get = 4 x 4 x 4 = 64
Now surface area of one cube = 6 x (1)²
= 6 x 1=6 cm²
and surface area of 64 cubes = 6 x 64 cm² = 384 cm²

Question 8.
The length of a hall is 18 m and the width 12 m. The sum of the areas of the floor and the flat roof is equal to the sum of the areas of the four walls. Find the height of the hall.
Solution:
Let h be the height of the room
Length (l) = 18 m
and width (b) = 12 m
Now surface area of floor and roof = 2 x lb = 2 x 18 x 12 m²
= 432 m²
and surface area of 4-walls = 2h (l + b)
= 2h(18 + 12) = 2 x 30h m² = 60h m²
∵ The surface are of 4-walls and area of floor and roof are equal
∴ 60h = 432
⇒ h = \(\frac { 432 }{ 60 }\) = \(\frac { 72 }{ 10 }\) m
∴ Height = 7.2m

Question 9.
Hameed has built a cubical water tank with lid for his house, with each other edge 1.5m long. He gets the outer surface of the tank excluding the base, covered with square tiles of side 25 cm. Find how much he would spend for the tiles, if the cost of tiles is ₹360 per dozen. [NCERT]
Solution:
Edge of cubical tank = 1.5 m
∴ Area of 4 walls = 4 (side)² = 4(1.5)² m² = 4 x 225 = 9 m²
Area of floor = (1.5)² = 2.25 m²
∴ Total surface area = 9 + 2.25 = 11.25 m²
Edge of square tile = 25 m = 0.25 m²
∴ Area of 1 tile = (0.25)2 = .0625 m²
RD Sharma Class 9 Solutions Chapter 18 Surface Areas and Volume of a Cuboid and Cube Ex 18.1 Q9.1

Question 10.
Each edge of a cube is increased by 50%. Find the percentage increase in the surface area of the cube.
Solution:
Let edge of a cube = a
Total surface area = 6a2
By increasing edge at 50%,
RD Sharma Class 9 Solutions Chapter 18 Surface Areas and Volume of a Cuboid and Cube Ex 18.1 Q10.1

Question 11.
A closed iron tank 12 m long, 9 m wide and 4 m deep is to be made. Determine the cost of iron sheet used at the rate of ₹5 per metre sheet, sheet being 2 m wide.
Solution:
Length of iron tank (l) = 12 m
Breadth (b) = 9 m
Depth (h) = 4 cm
RD Sharma Class 9 Solutions Chapter 18 Surface Areas and Volume of a Cuboid and Cube Ex 18.1 Q11.1

Question 12.
Ravish wanted to make a temporary shelter for his car by making a box-like structure with tarpaulin that covers all the four sides and the top of tire car (with the front face as a flap which can be rolled up). Assuming that the stitching margins are very small, and therefore negligible, how much tarpaulin would be required to make (he shelter of height 2.5 m with base dimensions 4 m x 3 m? [NCERT]
Solution:
Length of base (l) = 4m
Breadth (b) = 3 m
Height (h) = 2.5 m
RD Sharma Class 9 Solutions Chapter 18 Surface Areas and Volume of a Cuboid and Cube Ex 18.1 Q12.1

Question 13.
An open box is made of wood 3 cm thick. Its external length, breadth and height are 1.48 m, 1.16 m and 8.3 dm. Find the cost of painting the inner surface of ₹50 per sq. metre.
Solution:
Length of open wood box (L) = 1.48 m = 148 cm
Breadth (B) = 1.16 m = 116 cm
and height (H) = 8.3 dm = 83 cm
Thickness of wood = 3 cm
RD Sharma Class 9 Solutions Chapter 18 Surface Areas and Volume of a Cuboid and Cube Ex 18.1 Q13.1

Question 14.
The dimensions of a room are 12.5 m by 9 m by 7 m. There are 2 doors and 4 windows in the room; each door measures 2.5 m by 1.2 m and each window 1.5 m by 1 m. Find the cost of painting the walls at ₹3.50 per square metre.
Solution:
Length of room (l) = 12.5 m
Breadth (b) = 9 m
and height (h) = 7 m
∴ Total area of walls = 2h(l + b)
= 2 x 7[12.5 + 9] = 14 x 21.5 m² = 301 m²
Area of 2 doors of 2.5 m x 1.2 m
= 2 x 2.5 x 1.2 m² = 6 m²
and area of 4 window of 1.5 m x 1 m
= 4 x 1.5 x 1 = 6 m²
∴ Remaining area of walls = 301 – (6 + 6)
= 301 – 12 = 289 m²
Rate of painting the walls = ₹3.50 per m²
∴ Total cost = 289 x 3.50 = ₹1011.50

Question 15.
The paint in a certain container is sufficient to paint on area equal to 9.375 m2. How many bricks of dimension 22.5 cm x 10 cm x 7.5 cm can be painted out of this container? [NCERT]
Solution:
Area of place for painting = 9.375 m²
Dimension of one brick = 22.5 cm x 10 cm x 7.5 cm
∴ Surface area of one bricks = 2 (lb + bh + hl)
= 2[22.5 x 10 + 10 x 7.5 + 7.5 x 22.5] cm2
= 2[225 + 75 + 168.75]
= 2 x 468.75 cm² = 937.5 cm²
RD Sharma Class 9 Solutions Chapter 18 Surface Areas and Volume of a Cuboid and Cube Ex 18.1 Q15.1

Question 16.
The dimensions of a rectangular box are in the ratio of 2 : 3 : 4 and the difference between the cost of covering it with sheet of paper at the rates of ₹8 and ₹9.50 per m2 is ₹1248. Find the dimensions of the box.
Solution:
Ratio in the dimensions of a cuboidal box = 2 : 3 : 4
Let length (l) = 4x
Breadth (b) = 3.v
and height (h) = 2x
∴ Total surface area = 2 [lb + bh + hl]
RD Sharma Class 9 Solutions Chapter 18 Surface Areas and Volume of a Cuboid and Cube Ex 18.1 Q16.1

Question 17.
The cost of preparing the walls of a room 12 m long at the rate of ₹1.35 per square metre is ₹340.20 and the cost of matting the floor at 85 paise per square metre is ₹91.80. Find the height of the room.
Solution:
Cost of preparing walls of a room = ₹340.20
RD Sharma Class 9 Solutions Chapter 18 Surface Areas and Volume of a Cuboid and Cube Ex 18.1 Q17.1

Question 18.
The length and breadth of a hall are in the ratio 4 : 3 and its height is 5.5 metres. The cost of decorating its walls (including doors and windows) at ₹6.60 per square metre is ₹5082. Find the length and breadth of the room
Solution:
Ratio in length and breadth = 4:3
and height (h) = 5.5 m
Cost of decorating the walls of a room including doors and windows = ₹5082
Rate = ₹6.60 per m²
RD Sharma Class 9 Solutions Chapter 18 Surface Areas and Volume of a Cuboid and Cube Ex 18.1 Q18.1

Question 19.
A wooden bookshelf has external dimensions as follows: Height =110 cm, Depth = 25 cm, Breadth = 85 cm (see figure). The thickness of the plank is 5 cm everywhere. The external faces are to be polished and the inner faces are to be painted. If the rate of polishing is 20 paise per cm2 and the rate of painting is 10 paise per cm2. Find the total expenses required for polishing and painting the surface of the bookshelf. [NCERT]
Solution:
Length (l) = 85 cm
Breadth (b) = 25 cm
and height (h) = 110 cm
Thickness of plank = 5 cm
Surface area to be polished
= [(100 x 85) + 2 (110 x 25) + 2 (85 x 25) + 2 (110 x 5) + 4 (75 x 5)]
= (9350 + 5500 + 4250 + 1100 + 1500) cm² = 21700 cm²
RD Sharma Class 9 Solutions Chapter 18 Surface Areas and Volume of a Cuboid and Cube Ex 18.1 Q19.1

Hope given RD Sharma Class 9 Solutions Chapter 18 Surface Areas and Volume of a Cuboid and Cube Ex 18.1 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.