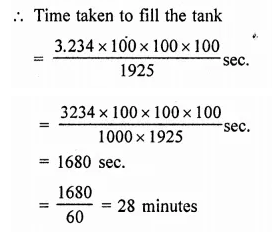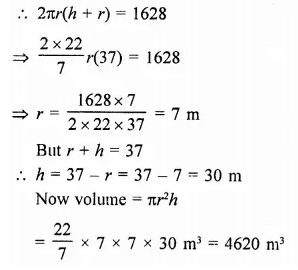Prasanna

NCERT Exemplar Solutions for Class 9 Science Chapter 11 Work, Power and Energy

by

NCERT Exemplar Solutions for Class 9 Science Chapter 11 Work, Power and Energy

These Solutions are part of NCERT Exemplar Solutions for Class 9 Science . Here we have given NCERT Exemplar Solutions for Class 9 Science Chapter 11 Work, Power and Energy

MULTIPLE CHOICE QUESTIONS

Question 1.
When a body falls freely towards the earth, then its total energy
(a) increases
(b) decreases
(c) remains constant
(d) first increases and then decreases,
Answer:
(c) Total energy = K.E. + P.E.
When a body falls freely, its K.E. increases and P.E. decreases but the sum of K.E and P.E. remains the same.

More Resources

Question 2.
A car is accelerated on a levelled road and attains a velocity 4 times of its initial velocity. In this process, the potential energy of the car
(a) does not change
(b) becomes twice to that of initial
(c) becomes 4 times that of initial
(d) becomes 16 times that of initial.
Answer:
(a). Potential energy does not depend on the velocity of a body.

Question 3.
In case of negative work, the angle between the force and displacement is
(a) 0°
(b) 45°
(c) 90°
(d) 180°.
Answer:
(d) Explanation : W = FS cos θ. When θ = 180°, cos 180° = – 1 and W = – FS

Question 4.
An iron sphere of mass 10 kg has the same diameter as an aluminium sphere of mass is 3.5 kg. Both spheres are dropped simultaneously from a tower.
When they are 10 m above the ground, they have the same
(a) acceleration
(b) momenta
(c) potential energy
(d) kinetic energy.
Answer:
(a). Freely falling bodies moves with constant acceleration.

Question 5.
A girl is carrying a school bag of 3 kg mass on her back and moves 200 m on a levelled road. The work done against the gravitational force will be (g = 10 m s-2)
(a) 6 x 103 J
(b) 6 J
(c) 0.6 J
(d) zero.
Answer:
(d) Explanation : W = FS cos 90° = 0.

Question 6.
Which one of the following is not the unit of energy ?
(a) joule
(b) newton metre
(c) kiiowatt
(d) kolwatt hour.
Answer:
(c) It is the unit of power.

Question 7.
The work done on an object does not depend upon the
(a) displacement
(b) force applied
(c) angle between force and displacement
(d) initial velocity of the object.
Answer:
(d) W = FS cos θ.

Question 8.
Water stored in a dam possesses
(a) no energy
(b) electrical energy
(c) kinetic energy
(d) potential energy
Answer:
(d). The energy possessed by a body by virtue of its position is called potential energy.

Question 9.
A body is falling from a height h. After it has fallen a height h/2, it will possess
(a) only potential energy
(b) only kinetic energy
(c) half potential and half kinetic energy
(d) more kinetic and less potential energy.
Answer:
(c).

SHORT ANSWER QUESTIONS

Question 10.
A rocket is moving up with a velocity u. If the velocity of this rocket is suddenly tripled, what will be the ratio of two kinetic energies ?
Answer:
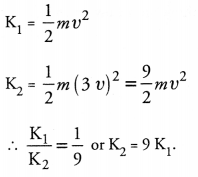
NCERT Exemplar Solutions for Class 9 Science Chapter 11 Work, Power and Energy image - 1

Question 11.
Avinash can run with a speed of 8 m s-1 against the frictional force of 10 N, and Kapil can move with a speed of 3 m s-1 against the frictional force of 25 N. Who is more powerful and why ?
Answer:
P = Fu
Power of Avinash = 10 x 8 = 80 W
Power of Kapil = 25 x 3 = 75 W
So, Avinash is more powerful.

Question 12.
A boy is moving on a straight road against a frictional force of 5 N. After travelling a distance of 1.5 km he forgot the correct path at a round about (Fig. 1) of radius 100 m.
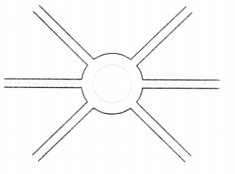
NCERT Exemplar Solutions for Class 9 Science Chapter 11 Work, Power and Energy image - 2
Answer:
However, he moves on the circular path for one and half cycle and then he moves forward upto 2.0 km. Calculate the work done by him.
Here, F = 5N, Distance travelled S = 1500 + 3 π r + 2000 = 4442.86 m
∴ W = F x S = 5 x 4442.86 = 22214.3 J.

Question 13.
Can any object have mechanical energy even if its momentum is zero ? Explain.
Answer:
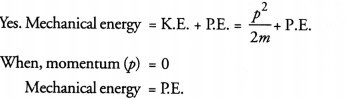
NCERT Exemplar Solutions for Class 9 Science Chapter 11 Work, Power and Energy image - 3

Question 14.
Can any object have momentum even if its mechanical energy is zero ? Explain.
Answer:
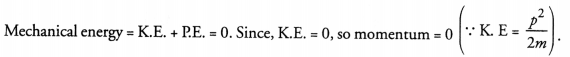
NCERT Exemplar Solutions for Class 9 Science Chapter 11 Work, Power and Energy image - 4

Question 15.
The power of a motor pump is 2 kW. How much water per minute the pump can raise to a height of 10 m ? (Given g = 10 m s-2).
Answer:
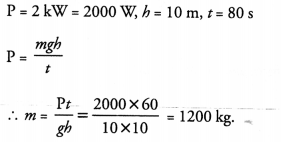
NCERT Exemplar Solutions for Class 9 Science Chapter 11 Work, Power and Energy image - 5

Question 16.
The weight of a person on a planet A is about half that on the earth. He can jump upto 0.4 m height on the surface of the earth. How high he can jump on the planet A ?
Answer:
NCERT Exemplar Solutions for Class 9 Science Chapter 11 Work, Power and Energy image - 6

Question 17.
The velocity of a body moving in a straight line is increased by applying a constant force F, for some distance in the direction of the motion. Prove that the increase in the kinetic energy of the body is equal to the work done by the force on the body.
Answer:
Consider a body or an object of mass m moving with velocity u. Let a force F be applied on the body so that the velocity attained by the body after travelling a distance S is v (Figure 5).
NCERT Exemplar Solutions for Class 9 Science Chapter 11 Work, Power and Energy image - 7
Work done by the force on the body is given by
W =      FS                                                                               …(i)
Since velocity of the body changes so the body is accelerated. Let a be the acceleration of the body. Therefore, according to Newton’s second law of motion,
F =     ma                                                                             …(ii)
Using eqn. (ii) in eqn. (i), we get
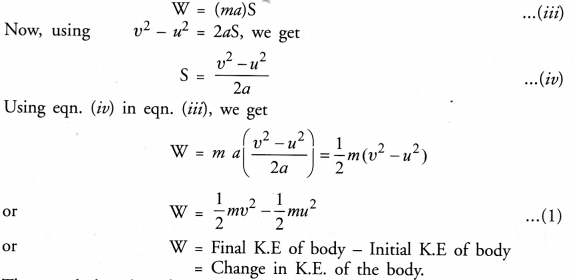
NCERT Exemplar Solutions for Class 9 Science Chapter 11 Work, Power and Energy image - 8
Thus, work done by a force on a body is equal to the change in kinetic energy of the body This is known as work-energy theorem.

Question 18.
Is it possible that an object is in the state of accelerated motion due to external force acting on it, but no work is being done by the force. Explain it with an example.
Answer:
Yes. When body moves in a circular path.

Question 19.
A ball is dropped from a height of 10 m. If the energy of the ball reduces by 40% after striking the ground, how much high can the ball bounce back ? (g = 10 m s-2). (CBSE 2013)
Answer:
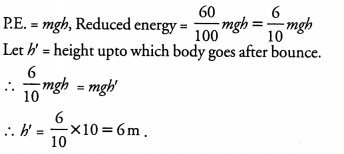
NCERT Exemplar Solutions for Class 9 Science Chapter 11 Work, Power and Energy image - 9

Question 20.
If an electric iron of 1200 W is used for 30 minutes everyday, find electric energy consumed in the month of April.
Answer:
Energy consumed in one day = P x t= 1200 W x ½ h = 600 Wh
Energy consumed in 30 days = 600 Wh x 30 = 1800 Wh =18 kWh.

LONG ANSWER QUESTIONS

Question 21.
A light and a heavy object have the same momentum. Find out the ratio of their kinetic energies. Which one has a larger kinetic energy ?
Answer:
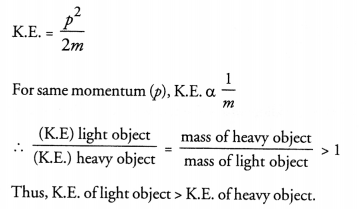
NCERT Exemplar Solutions for Class 9 Science Chapter 11 Work, Power and Energy image - 10

Question 22.
An automobile engine propels a 1000 kg car (A) along a levelled road at a speed of 36 km h-1. Find power if the opposing frictional force is 100 N. Now, suppose after travelling a distance of 200 m, this car collides with another stationary car (B) of same mass and comes to rest. Let its engine also stops at the same time. Now car (B) starts moving on the same level road without getting its engine started. Find the speed of car (B) just after the collision.
Answer:
Force = 100 N, v = 36 km h-1 = 36 x (5/18) = 10 m s-1
∴ Power, P = Force x velocity = 100 x 10 = 1000 W
According to law of conservation of linear momentum
Momentum of car A + Mementum of car B before collision = momentum of car A + momentum of car B after collision
i.e. 1000 x 10 + 1000 x 0 = 1000 x 0 + 1000 x v
∴ v = 10 m s-1
Thus, speed of car B just after collision =10 ms-1

Question 23.
A girl having mass of 35 kg sits on a trolley of mass 5 kg. The trolley is given an initial velocity of 4 ms-1 by applying a force. The trolley comes to rest after travelling a distance of 16m.
(a) How much work is done on the trolley ?
(b) How much work is done by the girl ?
Answer:
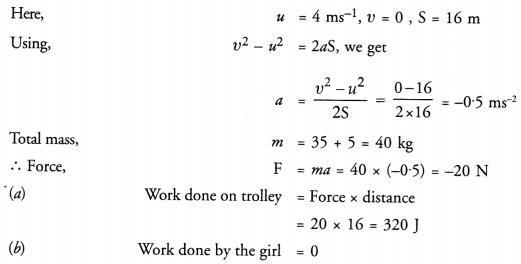
NCERT Exemplar Solutions for Class 9 Science Chapter 11 Work, Power and Energy image - 11

Question 24.
Four men lift a 250 kg box to a height of 1 m and hold it without raising or lowering it.
(a) How much work is done by the men in lifting the box ?
(b) How much work do they do in just holding it ?
(c) Why do they get tired while holding it ? (g = 10m s-2)
Answer:

Question 25.
(a) W = F x S = mgS= 250 x 10 x 1 =25.0 J.
(b) Zero. This is because displacement of box is zero.
(c) They get tired because muscular force applied by them is needed to balance the weight of the box.
Answer:
The Jog Falls in Karnataka State are nearly 200m high. 2000 tonnes of water falls from it in a minute. Calculate the equivalent power if all this energy can be utilized ? (g = 10 ms-2)
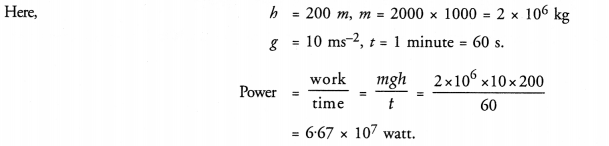
NCERT Exemplar Solutions for Class 9 Science Chapter 11 Work, Power and Energy image - 12

Question 26.
How is the power related to the speed at which a body can be lifted ? How many kilograms will a man working at the power of 100 W, be able to lift at constant speed of 1 ms-1 vertically ? (g = 10 ms-2)
Answer:
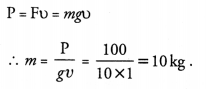
NCERT Exemplar Solutions for Class 9 Science Chapter 11 Work, Power and Energy image - 13

Question 27.
Define watt. Express kilowatt in terms of joule per second. A 150 kg car engine develops 500 W for each kg. What force does it exert in moving the car at a speed of 20 m s-1 ?
Answer:
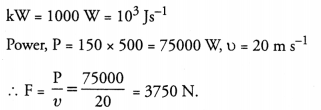
NCERT Exemplar Solutions for Class 9 Science Chapter 11 Work, Power and Energy image - 14

Question 28.
Compare the power at which each of the following is moving upwards against the force of gravity ? (given g = 10 ms-2)

  1. a butterfly of mass 1.0 g that flies upward at a rate of 0.5 m s-1 .
  2. a 250 g squirrel climbing up on a tree at a rate of 0.5 m s-1.

Answer:

  1. P = Fv = mgv = 1 x 10-3 x 10 x 0.5 = 5 x 10-3 W
  2. P = Fv = mg= 250 x 10-3 x 10 x 0.5 = 1.25 W.

Hope given NCERT Exemplar Solutions for Class 9 Science Chapter 11 Work, Power and Energy are helpful to complete your science homework.

If you have any doubts, please comment below. Learn Insta try to provide online science tutoring for you.

RS Aggarwal Class 8 Solutions Chapter 16 Parallelograms Ex 16B

by

RS Aggarwal Class 8 Solutions Chapter 16 Parallelograms Ex 16B

These Solutions are part of RS Aggarwal Solutions Class 8. RS Aggarwal Solutions Class 8 Chapter 16 Parallelograms Ex 16B.

Other Exercises

Questions Tick the correct answer in each of the following.

Question 1.
Solution:
Answer = (c)
The diagonals of a rhombus are not necessarily equal but the diagonals in rectangle, square and isosceles trapezium are always equal.

Question 2.
Solution:
Answer = (c)
Each side of a rhombus
RS Aggarwal Class 8 Solutions Chapter 16 Parallelograms Ex 16B 2.1

Question 3.
Solution:
Answer = (b)
The sum of adjacent angles of a || gm = 180°
2x + 25° + 3x – 5° = 180°
=> 5x + 20° = 180°
=> 5x = 180° – 20° = 160°
=> x = \(\\ \frac { 160 }{ 5 } \)
= 32°

Question 4.
Solution:
Answer = (a)
The diagonals in rhombus, kite intersect each other at right angles.
But the diagonals of parallelogram do not necessarily intersect at right angles.

Question 5.
Solution:
Answer = (c)
Let l = 4x, b = 3x,
Then (diagonal)² = l² + b²
=> (25)² = 16x² + 9x²
=> 25x² = 625
=> x² = 25
=> x = 5
=> l = 4x = 4 x 5 = 20cm
b = 3x = 3 x 5 = 15cm
Perimeter = 2(l + b) = 2 (20 + 15)
= 2 x 35 = 70 cm

Question 6.
Solution:
Answer = (d)
AP and BP are the bisector of ∠A and ∠B
Sum of two adjacent angles of a ||gm = 180°
or ∠A + ∠B = 180°
RS Aggarwal Class 8 Solutions Chapter 16 Parallelograms Ex 16B 6.1
But ∠1 = \(\\ \frac { 1 }{ 2 } \) ∠A and ∠2 =\(\\ \frac { 1 }{ 2 } \) ∠B
∠1 + ∠2 = \(\\ \frac { 1 }{ 2 } \) ∠A + \(\\ \frac { 1 }{ 2 } \) ∠B
= \(\\ \frac { 1 }{ 2 } \) (∠A + ∠B)
= 180° x \(\\ \frac { 1 }{ 2 } \) = 90°
∠P = 180° – (∠1 + ∠2)
= 180° – 90° = 90°

Question 7.
Solution:
Answer = (b)
Let one adjacent angle = x
Then second angle (smallest) = \(\frac { 2 }{ 3 } x \)
x + \(\frac { 2 }{ 3 } x \) = 180°
= \(\frac { 5 }{ 3 } x \) = 180°
=> x = 180° x \(\\ \frac { 3 }{ 5 }\) = 108°
=> Smallest angle = 108° x \(\\ \frac { 2 }{ 3 }\) = 72°

Question 8.
Solution:
Answer = (a)
The diagonals of square, rhombus bisect the interior angle but the diagonals of a rectangle do not.

Question 9.
Solution:
Answer = (d)
Sides of a square are equal
2x + 3 = 3x – 5
=> 3x – 2x = 3 + 5
=> x = 8

Question 10.
Solution:
Answer = (c)
Let smallest angle = x
then largest angle = 2x – 24°
But x + 2x – 24° = 180°
=> 3x – 24° = 180°
=> 3x = 180° + 24 = 204°
=> x = \(\\ \frac { 204 }{ 3 }\) = 68°
largest angle = 180° – 68° = 112°

Hope given RS Aggarwal Solutions Class 8 Chapter 16 Parallelograms Ex 16B are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 9 Solutions Chapter 19 Surface Areas and Volume of a Circular Cylinder Ex 19.2

by

RD Sharma Class 9 Solutions Chapter 19 Surface Areas and Volume of a Circular Cylinder Ex 19.2

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 19 Surface Areas and Volume of a Circular Cylinder Ex 19.2

Other Exercises

Question 1.
A soft drink is available in two packs – (i) a tin can with a rectangular base of length 5 cm and width 4 cm, having a height of 15 cm and
(ii) a plastic cylinder with circular base of diameter 7 cm and height 10 cm. Which container has greater capacity and by how much? [NCERT]
Solution:
In first case, in a rectangular container of soft drink, the length of base = 5 cm
and Width = 4 cm
Height = 15 cm
∴ Volume of soft drink = lbh = 5 x 4 x 15 = 300 cm3
and in second case, in a cylindrical container, diameter of base = 7 cm
RD Sharma Class 9 Solutions Chapter 19 Surface Areas and Volume of a Circular Cylinder Ex 19.2 Q1.1
∴ The soft drink in second container is greater and how much greater = 385 cm – 380 cm2 = 85 cm2

Question 2.
The pillars of a temple are cylindrically shaped. If each pillar has a circular base of radius 20 cm and height 10 m. How much concrete mixture would be required to build 14 such pillars? [NCERT]
Solution:
Radius of each pillar (r) = 20 cm
RD Sharma Class 9 Solutions Chapter 19 Surface Areas and Volume of a Circular Cylinder Ex 19.2 Q2.1

Question 3.
The inner diameter of a cylindrical wooden pipe is 24 cm and its outer diameter is 28 cm. The length of the pipe is 35 cm. Find the mass of the pipe, if 1 cm3 of wood has a mass of 0.6 gm. [NCERT]
Solution:
Inner diameter of a cylindrical wooden pipe = 24 cm
RD Sharma Class 9 Solutions Chapter 19 Surface Areas and Volume of a Circular Cylinder Ex 19.2 Q3.1

Question 4.
If the lateral surface of a cylinder is 94.2 cm2 and its height is 5 cm, find:
(i) radius of its base
(ii) volume of the cylinder [Use π = 3.14] [NCERT]
Solution:
Lateral surface area of a cylinder = 94.2 cm2
RD Sharma Class 9 Solutions Chapter 19 Surface Areas and Volume of a Circular Cylinder Ex 19.2 Q4.1

Question 5.
The capacity of a closed cylindrical vessel of height 1 m is 15.4 litres. How many square metres of metal sheet would be needed to make it? [NCERT]
Solution:
The capacity of a closed cylindrical vessel = 15.4 l
RD Sharma Class 9 Solutions Chapter 19 Surface Areas and Volume of a Circular Cylinder Ex 19.2 Q5.1

Question 6.
A patient in a hospital is given soup daily in a cylindrical bowl of diameter 7 cm. If the bowl is filled with soup to a height of 4 cm, how much soup the hospital has to prepare daily to serve 250 patients? [NCERT]
Solution:
Diameter of the cylindrical bowl = 7 cm
∴ Radius (r) = \(\frac { 7 }{ 2 }\)cm
Level of soup in it = 4 cm
∴ Volume of soup in one bowl for one patient
RD Sharma Class 9 Solutions Chapter 19 Surface Areas and Volume of a Circular Cylinder Ex 19.2 Q6.1

Question 7.
A hollow garden roller, 63 cm wide with a girth of 440 cm, is made of 4 cm thick iron. Find the volume of the iron.
Solution:
Width of hollow cylinder (A) = 63 cm
Girth = 440 cm
RD Sharma Class 9 Solutions Chapter 19 Surface Areas and Volume of a Circular Cylinder Ex 19.2 Q7.1

Question 8.
The cost of painting the total outside surface of a closed cylindrical oil tank at 50 paise per square decimetre is ₹ 198. The height of the tank is 6 times the radius of the base of the tank. Find the volume corrected to 2 decimal places.
Solution:
Rate of painting = 50 paise per dm2
Total cost = ₹198
RD Sharma Class 9 Solutions Chapter 19 Surface Areas and Volume of a Circular Cylinder Ex 19.2 Q8.1
RD Sharma Class 9 Solutions Chapter 19 Surface Areas and Volume of a Circular Cylinder Ex 19.2 Q8.2

Question 9.
The radii of two cylinders are in the ratio 2 : 3 and their heights are in the ratio 5:3. Calculate the ratio of their volumes and the ratio of their curved surfaces.
Solution:
Ratio in radii of two cylinders = 2:3
and ratio in their heights = 5:3
Let radius of the first cylinder (r1) = 2x
and radius of second cylinder (r2) = 3x
and height of first cylinders (h1) = 5y
and height of second cylinder (h2) = 3y
(i) Now volume of the first cylinder = πr2h = π(2x)2 x 5y = 20πx22y
and volume of tlie second cylinder = π(3x)2 x 3y = π x 9×2 x 3y = 27πx2y
Now ratio in their volume
= 20πx2y : 21πx2y = 20 : 27
(ii) Curved surface area of first cylinder = 2πrh = 2π x 2x x 5y =20πxy
and curved surface area of second cylinder = 2π x 3x x = 1 8πxy
∴ Ratio in their curved surface area
= 20πxy : 18πxy = 10 : 9

Question 10.
The ratio between the curved surface area and the total surface area of a right circular cylinder is 1 : 2. Find the volume of the cylinder, if its total surface area is 616 cm2.
Solution:
Ratio in curved surface area and total surface area of a cylinder =1:2
Total surface area = 616 cm2
RD Sharma Class 9 Solutions Chapter 19 Surface Areas and Volume of a Circular Cylinder Ex 19.2 Q10.1

Question 11.
The curved surface area of a cylinder is 1320 cm2 and its base had diameter 21 cm. Find the height and the volume of the cylinder. [Use π = 22/7]
Solution:
Curved surface area of a cylinder = 1320 cm2
Diameter of the base = 21 cm
RD Sharma Class 9 Solutions Chapter 19 Surface Areas and Volume of a Circular Cylinder Ex 19.2 Q11.1

Question 12.
The ratio between the radius of the base and the height of a cylinder is 2 : 3. Find the total surface area of the cylinder, if its volume is 1617 cm3.
Solution:
Ratio between radius and height of a cylinder = 2:3
Volume =1617 cm3
Let radius (r) = 2x
Then height (h) = 3x
∴ Volume = πr2h
RD Sharma Class 9 Solutions Chapter 19 Surface Areas and Volume of a Circular Cylinder Ex 19.2 Q12.1
RD Sharma Class 9 Solutions Chapter 19 Surface Areas and Volume of a Circular Cylinder Ex 19.2 Q12.2

Question 13.
A rectangular sheet of paper, 44 cm x 20 cm, is rolled along its length of form a cylinder. Find the volume of the cylinder so formed.
Solution:
Length of sheet = 44 cm
Breadth = 20 cm
By rolling along length, the height of cylinder (h) = 20cm
and circumference of the base = 44cm
RD Sharma Class 9 Solutions Chapter 19 Surface Areas and Volume of a Circular Cylinder Ex 19.2 Q13.1

Question 14.
The curved surface area of a cylindrical pillar is 264 m2 and its volume is 924 m3. Find the diameter and the height of the pillar.
Solution:
Curved surface area of a pillar = 264 m2
and volume = 924 m3
Let r be the radius and It be height, then 2πrh = 264
RD Sharma Class 9 Solutions Chapter 19 Surface Areas and Volume of a Circular Cylinder Ex 19.2 Q14.1
RD Sharma Class 9 Solutions Chapter 19 Surface Areas and Volume of a Circular Cylinder Ex 19.2 Q14.2

Question 15.
Two circular cylinders of equal volumes have their heights in the ratio 1 : 2. Find the ratio of their radii.
Solution:
Volumes of two cylinders are equal Ratio in their height h1 :h2 = 1: 2
RD Sharma Class 9 Solutions Chapter 19 Surface Areas and Volume of a Circular Cylinder Ex 19.2 Q15.1

Question 16.
The height of a right circular cylinder is 10.5 m. Three times the sum of the areas of its two circular faces is twice the” area of the curved surface. Find the volume of the cylinder.
Solution:
Height of a right circular cylinder = 10.5 m
3 x sum of areas of two circular faces
= 2 x area of curved surface
Let r be that radius,
RD Sharma Class 9 Solutions Chapter 19 Surface Areas and Volume of a Circular Cylinder Ex 19.2 Q16.1

Question 17.
How many cubic metres of earth must be dugout to sink a well 21 m deep and 6 m diameter? Find the cost of plastering the inner surface of the well at ₹9.50 per m2.
Solution:
Diameter of a well = 6 m
∴ Radius (r) = \(\frac { 6 }{ 2 }\) = 3 m
Depth (h) = 21 m
∴ Volume of earth dugout = πr2h
RD Sharma Class 9 Solutions Chapter 19 Surface Areas and Volume of a Circular Cylinder Ex 19.2 Q17.1

Question 18.
The trunk of a tree is cylindrical and its circumference is 176 cm. If the length of the trunk is 3 m. Find the volume of the timber that can be obtained from the trunk.
Solution:
Circumference of a cylindrical trunk of a tree = 176 cm
RD Sharma Class 9 Solutions Chapter 19 Surface Areas and Volume of a Circular Cylinder Ex 19.2 Q18.1

Question 19.
A cylindrical container with diameter of base 56 cm contains sufficient water to submerge a rectangular solid of iron with dimensions 32 cm x 22 cm x 14 cm. Find the rise in the level of the water when the solid is completely submerged.
Solution:
Diameter of cylindrical container = 56 cm
∴ Radius (r) = \(\frac { 56 }{ 2 }\) = 28 cm
Dimensions of a rectangular solid are = 32 cm x 22 cm x 14 cm
∴ Volume of solid = lbh
= 32 x 22 x 14 = 9856 cm3
∴ Volume of water in the container = 9856 cm3
Let h be the level of water, then
πr2h = 9856
RD Sharma Class 9 Solutions Chapter 19 Surface Areas and Volume of a Circular Cylinder Ex 19.2 Q19.1

Question 20.
A cylindrical tube, open at both ends, is made of metal. The internal diameter of the tube is 10.4 cm and its length is 25 cm. The thickness of the metal is 8 mm everywhere. Calculate the volume of the metal.
Solution:
Length of metallic tube = 25 cm
Inner diameter = 10.4 cm
∴ Radius (r) = \(\frac { 10.4 }{ 2 }\) = 5.2 cm
Thickness of metal = 8 mm
∴ Outer radius (R) = 5.2 + 0.8 = 6.0 cm
Volume of metal used = π(R2 – r2) x h
RD Sharma Class 9 Solutions Chapter 19 Surface Areas and Volume of a Circular Cylinder Ex 19.2 Q20.1

Question 21.
From a tap of inner radius 0.75 cm, water flows at the rate of 7 m per second. Find the volume in litres of water delivered by the pipe in one hour.
Solution:
Inner radius of a tap = 0.75 cm
Speed of flow of water in it = 7 m/s
Time = 1 hour
∴ Length of flow of water (h)
= 7 x 60 x 60 m = 25200 m
∴ Volume of water = πr2h
RD Sharma Class 9 Solutions Chapter 19 Surface Areas and Volume of a Circular Cylinder Ex 19.2 Q21.1

Question 22.
A rectangular sheet of paper 30 cm x 18 cm can be transformed into the curved surface of a right circular cylinder in two ways i.e., either by rolling the paper along its length or by rolling it along its breadth. Find the ratio of the volumes of the two cylinders thus formed.
Solution:
Size of rectangular sheet = 30 cm x 18 cm
∴ Length of sheet = 30 cm
and breadth = 18 cm
By folding length wise,
Height = 18 cm
and circumference = 30 cm
RD Sharma Class 9 Solutions Chapter 19 Surface Areas and Volume of a Circular Cylinder Ex 19.2 Q22.1
RD Sharma Class 9 Solutions Chapter 19 Surface Areas and Volume of a Circular Cylinder Ex 19.2 Q22.2

Question 23.
How many litres of water flow out of a pipe having an area of cross-section of 5 cm2 in one minute, if the speed of water in the pipe is 30 cm/sec?
Solution:
Area of the cross-section of the pipe = 5 cm2
Speed of water flow = 30 cm/sec
Period = 1 minute
∴ Flow of water in 1 minute = 30 x 60 cm = 1800 cm
Area of mouth of pipe = 5 cm2
∴ Volume = 1800 x 5 = 9000 cm3
Volume of water in litres = 9000 ml
RD Sharma Class 9 Solutions Chapter 19 Surface Areas and Volume of a Circular Cylinder Ex 19.2 Q23.1

Question 24.
Find the cost of sinking a tubewell 280 m deep, having diameter 3 m at the rate of ₹3.60 per cubic metre. Find also the cost of cementing its inner curved surface at ₹2.50 per square metre.
Solution:
Depth of well (h) = 280 m
Diameter = 3 m
RD Sharma Class 9 Solutions Chapter 19 Surface Areas and Volume of a Circular Cylinder Ex 19.2 Q24.1

Question 25.
Find the length of 13.2 kg of copper wire of diameter 4 mm, when 1 cubic cm of copper weighs 8.4 gm.
Solution:
Weights of copper wire = 13.2 kg
Diamter = 4 mm
RD Sharma Class 9 Solutions Chapter 19 Surface Areas and Volume of a Circular Cylinder Ex 19.2 Q25.1

Question 26.
A solid cylinder has a total surface area of 231 cm2. Its curved surface area is \(\frac { 2 }{ 3 }\) of the total surface area. Find the volume of the cylinder.
Solution:
Surface area of solid cylinder = 231 cm2
and curved surface area = \(\frac { 2 }{ 3 }\) of 231 cm2
RD Sharma Class 9 Solutions Chapter 19 Surface Areas and Volume of a Circular Cylinder Ex 19.2 Q26.1
RD Sharma Class 9 Solutions Chapter 19 Surface Areas and Volume of a Circular Cylinder Ex 19.2 Q26.2

Question 27.
A well with 14 m diameter is dug 8 m deep. The earth taken out of it has been evenly spread all around it to a width of 21 m to form an embankment. Find the height of the embankment.
Solution:
Diameter of a well = 14 m
∴ Radius (r) = y = 7 m
Depth (h) = 8 m
∴ Volume of the earth dugout = πr2h
RD Sharma Class 9 Solutions Chapter 19 Surface Areas and Volume of a Circular Cylinder Ex 19.2 Q27.1
RD Sharma Class 9 Solutions Chapter 19 Surface Areas and Volume of a Circular Cylinder Ex 19.2 Q27.2

Question 28.
The difference between inside and outside surfaces of a cylindrical tube 14 cm long is 88 sq. cm. If the volume of the tube is 176 cubic cm, find the inner and outer radii of the tube.
Solution:
Length of cylindrical tube = 14 cm
Difference betveen the outer surface and inner surface = 88 cm2
and volume of the tube = 176 cm3
Let R and r be the outer and inner radius of the tube
RD Sharma Class 9 Solutions Chapter 19 Surface Areas and Volume of a Circular Cylinder Ex 19.2 Q28.1
RD Sharma Class 9 Solutions Chapter 19 Surface Areas and Volume of a Circular Cylinder Ex 19.2 Q28.2

Question 29.
Water flows out through a circular pipe whose internal diameter is 2 cm, at the rate of 6 metres per second into a cylindrical tank. The radius of whose base is 60 cm. Find the rise in the level of water in 30 minutes?
Solution:
Internal diameter of the pipe = 2 cm
∴ Radius (r) = \(\frac { 2 }{ 2 }\) = 1 cm
Speed of water flow = 6m per second Water in 30 minutes (h) = 6 x 60 x 30 m = 10800 m
Volume of water = πr2h
RD Sharma Class 9 Solutions Chapter 19 Surface Areas and Volume of a Circular Cylinder Ex 19.2 Q29.1

Question 30.
A cylindrical water tank of diameter 1.4 m and height 2.1 m is being fed by a pipe of diameter 3.5 cm through which water flows at the rate of 2 metre per second. In how much time the tank will be filled?
Solution:
Diameter of cylindrical tank = 1.4 m
∴ Radius (r) = \(\frac { 1.4 }{ 2 }\) = 0.7 m
and height (h) = 2.1 m
∴ Volume of water in the tank = πr2h
RD Sharma Class 9 Solutions Chapter 19 Surface Areas and Volume of a Circular Cylinder Ex 19.2 Q30.1
RD Sharma Class 9 Solutions Chapter 19 Surface Areas and Volume of a Circular Cylinder Ex 19.2 Q30.2

Question 31.
The sum of the radius of the base and height of a solid cylinder is 37 m. If the total surface area of the solid cylinder is 1628 m2. Find the volume of the cylinder.
Solution:
Sum of radius and height of a cylinder = 37 m
Let r be the radius and h be the height, then r + h = 37m …(i)
Total surface area of a solid cylinder = 1628m3
RD Sharma Class 9 Solutions Chapter 19 Surface Areas and Volume of a Circular Cylinder Ex 19.2 Q31.1

Question 32.
A well with 10 m inside diameter is dug 8.4 m deep. Earth taken out of it is spread all around it to a width of 7.5 m to form an embankment. Find the height of the embankment.
Solution:
Diameter of the well = 10 m 10
∴ Radius (r) = \(\frac { 10 }{ 2 }\) = 5 m
Depth (h) = 8.4 m
∴ Volume of earth dugout = πr2h
RD Sharma Class 9 Solutions Chapter 19 Surface Areas and Volume of a Circular Cylinder Ex 19.2 Q32.1

Hope given RD Sharma Class 9 Solutions Chapter 19 Surface Areas and Volume of a Circular Cylinder Ex 19.2 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 8 Solutions Chapter 16 Parallelograms Ex 16A

by

RS Aggarwal Class 8 Solutions Chapter 16 Parallelograms Ex 16A

These Solutions are part of RS Aggarwal Solutions Class 8. RS Aggarwal Solutions Class 8 Chapter 16 Parallelograms Ex 16A.

Other Exercises

Question 1.
Solution:
In ||gm ABCD,
∠A = 110°
But ∠ C = ∠ A {Opposite angles of a ||gm are equal}
RS Aggarwal Class 8 Solutions Chapter 16 Parallelograms Ex 16A 1.1
∴ ∠C = 110°
But ∠A + ∠B = 180°
(Sum of adjacent angles)
=> 110° + ∠B = 180°
=> ∠B – 180° – 110° = 70°
But ∠ D = ∠ B (opposite angles)
∴ ∠ D = 70°
Hence ∠B = 70°, ∠C = 110° and ∠D = 70° Ans.

Question 2.
Solution:
In a parallelogram, sum of two adjacent angles is 180°
But these are equal to each other
∴ Each angle will be \(\frac { 180^{ o } }{ 2 } \)
= 90° Ans.

Question 3.
Solution:
The ratio between two adjacent angles of a ||gm ABCD are in the ratio 4 : 5
RS Aggarwal Class 8 Solutions Chapter 16 Parallelograms Ex 16A 3.1
Let ∠ A = 4x and ∠ B = 5x
But ∠A + ∠B = 180°
=> 4x + 5x = 180°
=> 9x = 180°
∴ x = \(\frac { 180^{ o } }{ 9 } \)
= 20°
∴ ∠A = Ax = 4 x 20° = 80°
∠B = 5x = 5 x 20 = 100° Ans.

Question 4.
Solution:
In || gm ABCD, ∠ A and ∠ B are two adjacent angles
Let ∠ A = (3x – 4)° and ∠ B = (3x + 16)°
But ∠A + ∠B = 180°
RS Aggarwal Class 8 Solutions Chapter 16 Parallelograms Ex 16A 4.1
=> (3x – 4)° + (3x + 16) = 180°
=> 3x – 4° + 3x + 16° = 180°
=> 6x + 12° = 180°
=> 6x= 180° – 12°
=> 6x = 168
=> x = \(\\ \frac { 168 }{ 6 } \) = 28°
∴ x = 28°
Now ∠A = 3x – 4 = 3 x 28° – 4° = 84° – 4° = 80°
∠B = 3x + 16
= 3 x 28 + 16
= 84°+ 16° = 100°
But ∠C = ∠A (opposite angles of ||gm)
∴ ∠ C = 80°
Similarly ∠ D = ∠ B = 100°
Hence ∠A = 80°, ∠B = 100°, ∠C = 80° and ∠D= 100° Ans.

Question 5.
Solution:
In ||gm ABCD, ∠A and ∠C are opposite angles.
∴ ∠A = ∠C= 130°
RS Aggarwal Class 8 Solutions Chapter 16 Parallelograms Ex 16A 5.1
But ∠A = ∠C (opposite angles)
∴ ∠A = ∠C
= \(\frac { 130^{ o } }{ 2 } \)
= 65°
But ∠A + ∠B = 180°
(sum of adjacent angles)
=> 65° + ∠B = 180°
=> ∠B = 180° – 65° = 115°
But ∠ D = ∠ B (opposite angles)
∴ ∠D = 115°
Hence ∠A = 65°, ∠B = 115°, ∠C = 65° and ∠ D = 115° Ans.

Question 6.
Solution:
Let ABCD is a parallelogram in which AB : BC = 5:3
Let AB = 5x: and BC = 3x.
RS Aggarwal Class 8 Solutions Chapter 16 Parallelograms Ex 16A 6.1
But perimeter = 64 cm.
∴ 2(5x + 3x) = 64
=> 2 x 8x = 64
=> 16x = 64
x = \(\\ \frac { 64 }{ 16 } \)
= 4
∴ AB = 5x = 5 x 4 = 20 cm
BC = 3x = 3 x 4=12 cm
But CD = AB and AD = BC
(opposite sides of ||gm)
∴ CD = 20 cm and AD = 12 cm Ans.

Question 7.
Solution:
Perimeter of parallelogram ABCD = 140 cm.
=> ∴ 2 (AB + BC) = 140 cm.
=> AB + BC = \(\\ \frac { 140 }{ 2 } \) = 70 cm.
Let BC = x
RS Aggarwal Class 8 Solutions Chapter 16 Parallelograms Ex 16A 7.1
then AB = x + 10
∴ x + x + 10 = 70
=> 2x + 10 = 70
=> 2x = 70 – 10 = 60
=>x = \(\\ \frac { 60 }{ 2 } \) = 30
∴ BC = 30 cm. and
AB = 30 + 10 = 40 cm.
But AD = BC and CD = AB
(Opposite sides of parallelogram)
∴ AD = 30 cm. and CD = 40 cm.

Question 8.
Solution:
In rectangle ABCD, AC is diagonal BM ⊥ AC and DN ⊥ AC.
Now, we have to prove that
∆BMC ≅ ∆DNA
In ∆BMC and ∆DNA,
BC = AD (opposite sides of the rectangle)
∠M = ∠N (each = 90°)
∠BCM = ∠D AN (Alternate angles)
∴ ∆BMC ≅ ∆DNA
(S.A.A. axiom of congruency)
∴ BM = DN (c.p .c.t.)

Question 9.
Solution:
ABCD is a parallelogram.
AE and CF are the bisectors of ∠A and ∠C respectively.
In ∆ADE and ∆CBF,
AD = BC
(Opposite sides of the parallelogram)
∠D = ∠B
(Opposite angles of the parallelogram)
∠DAE = ∠FCB (\(\\ \frac { 1 }{ 2 } \) of equal angles)
∴ ∆ADE ≅ ∆CBF
(S.A.A. axiom of congruency)
∴ DE = BF (c.p.c.t.)
But CD = AB
(Opposite sides of the parallelogram)
∴ CD – DE = AB – BF
=> EC = AF
and AB || CD
∴ AFCE is a parallelogram
∴ AE || CF.

Question 10.
Solution:
Let ABCD is a rhombus AC and BD are its diagonals which bisect each other at right angles at O.
AC = 16cm and BD = 12cm
∴ AO = \(\\ \frac { 16 }{ 2 } \) = 8cm
RS Aggarwal Class 8 Solutions Chapter 16 Parallelograms Ex 16A 10.1
BO = \(\\ \frac { 12 }{ 2 } \) = 6 cm
Now, in right ∆AOB
AB² = AO² + BO²
(Pythagorus Theorem)
= (8)² + (6)²
= 64 + 36 = 100 = (10)²
∴ AB = 10 cm
But all the sides of a rhombus are equal
∴ Each side will be 10 cm Ans.

Question 11.
Solution:
In square ABCD, AC is its diagonal
∴ Diagonals of a square bisect each angle at the vertex
∴ ∠ CAD = ∠ CAB
But ∠ DAB = 90° (Angle of a square)
∴ ∠ CAD = ∠ CAB = \(\\ \frac { 1 }{ 2 } \) ∠ DAB
= \(\\ \frac { 1 }{ 2 } \) x 90° = 45°
Hence ∠ CAD = 45° Ans.

Question 12.
Solution:
Let ABCD is a rectangle
AB : BC = 5 : 4
Let AB = 5x and BC = 4x.
But perimeter = 90cm
RS Aggarwal Class 8 Solutions Chapter 16 Parallelograms Ex 16A 12.1
2(AB + BC) = 90
=> 2(5x + 4x) = 90
=> 2 x 9x = 90
=> 18x = 90
x = \(\\ \frac { 90 }{ 18 } \) = 5
∴ Length (AB) = 5x = 5 x 5 = 25 cm
Breadth (BC) = 4x = 4 x 5 = 20 cm Ans.

Question 13.
Solution:
(i) It is a rectangle
(ii) Square
(iii) rhombus
(iv) rhombus
(v) square
(vi) rectangle.

Question 14.
Solution:
(i) False
(ii) False
(iii) False
(iv) False
(v) False
(vi) True
(vii) True
(viii) True
(ix) False
(x) True

 

Hope given RS Aggarwal Solutions Class 8 Chapter 16 Parallelograms Ex 16A are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 8 Solutions Chapter 15 Quadrilaterals Ex 15

by

RS Aggarwal Class 8 Solutions Chapter 15 Quadrilaterals Ex 15

These Solutions are part of RS Aggarwal Solutions Class 8. Here we have given RS Aggarwal Class 8 Solutions Chapter 15 Quadrilaterals Ex 15.

Question 1.
Solution:
(i) Four
(ii) Four
(iii) 4, collinear
(iv) two
(v) opposite
(vi) 360°

Question 2.
Solution:
(i) There are four pairs of adjacent sides which are (AB, BC), (BC, CD), (CD, DA) and (DA, AB)
(ii) There are two pairs of opposite sides which are (AB, CD) and (BC, AD)
(iii) There are four pairs of adjacent angles which are (∠ A, ∠ B), (∠ B, ∠ C), (∠ C, ∠ D) and (∠ D, ∠ A)
(iv) There are two pairs of opposite angles which are (∠A, ∠C) and (∠B, ∠D)
(v) There are two diagonals which are AC and BD.

Question 3.
Solution:
Given : ABCD is a quadrilateral
RS Aggarwal Class 8 Solutions Chapter 15 Quadrilaterals Ex 15 3.1
To prove : ∠A + ∠B + ∠C + ∠D = 360°
Construction : Join BD
Proof : In ∆ ABD,
∠ A + ∠1 + ∠ 4 = 180° (sum of angles of a triangle)
Similarly ∠2 + ∠C + ∠ 3 = 180° Adding we get,
∠ A + ∠1 + ∠4 + ∠2 + ∠C + ∠ 3
= 180° + 180°
=> ∠A + ∠1 + ∠2 + ∠C + ∠3 + ∠4 = 360°
=> ∠A + ∠B + ∠C + ∠D = 360° Hence proved.

Question 4.
Solution:
We know that
Sum of 4 angles of a quadrilateral = 360°
But sum of 3 angles = 76° + 54° + 108°
= 238°
4th angle = 360 – 238°
= 122°
Hence, measure of fourth angle = 122° Ans

Question 5.
Solution:
Ratio of four angles of a quadrilateral = 3 : 5 : 7 : 9
Let these angles be 3x, 5x, 7x and 9x
then 3x + 5x + 7x + 9x = 360° (sum of angles)
=> 24x = 360°
First angle = 3x = 3 x 15° = 45°
Second angle = 5x = 5 x 15° = 75°
Third angle = 7x = 7 x 15° = 105°
Fourth angle = 9x = 9 x 15° = 135° Ans.

Question 6.
Solution:
Three acute angles of a quadrilateral are 75° each
Sum of three angles = 3 x 75° = 225°
But sum of 4 angles = 360°
Fourth angle = 360° – 225°
= 135° Ans.

Question 7.
Solution:
Sum of 4 angles of a quadrilateral 360°
One angles = 120°
Sum of other three angles = 360° – 120° = 240°
But each of these 3 angles are equal
Each of equal angles = \(\frac { 240^{ o } }{ 3 } \)
= 80°

Question 8.
Solution:
Sum of 4 angles of a quadrilateral = 360°
Sum of two angles = 85° + 75° = 160°
Sum of other two angles = 360° – 160° = 200°
But each of these two angles are equal
Measure of each equal angle = \(\frac { 200^{ o } }{ 2 } \)
= 100° Ans.

Question 9.
Solution:
In quadrilateral ABCD
∠C = 100°, ∠D = 60°
and ∠A + ∠B + ∠C + ∠D = 360°
(sum of angles of a quadrilateral)
∴ ∠ A + ∠ B = 360° – (100° + 60°)
= 360° – 160° = 200°
But AP and BP are the bisectors of ∠ A and ∠ B
∴ \(\\ \frac { 1 }{ 2 } \) – (∠ A + ∠B) = 200° x \(\\ \frac { 1 }{ 2 } \) = 100°
i.e. ∠ 1 + ∠2 = 100°
But in ∆ APB,
∠1 + ∠2 + ∠P = 180°
=> 100° + ∠P = 180°
=> ∠P = 180° – 100° = 80°
or ∠APB = 80° Ans.

 

Hope given RS Aggarwal Class 8 Solutions Chapter 15 Quadrilaterals Ex 15 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for yo