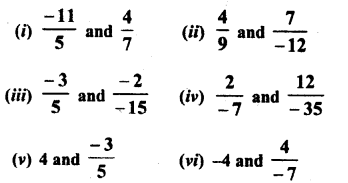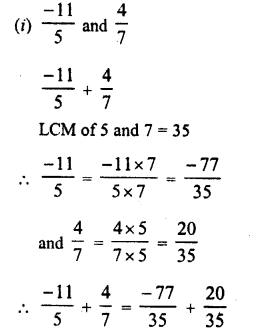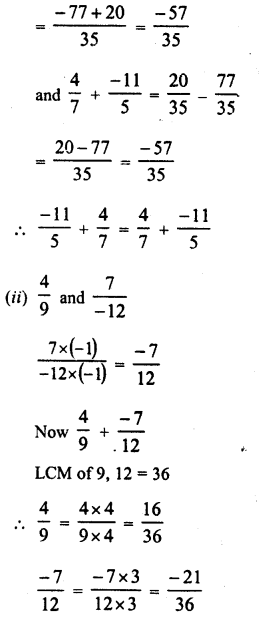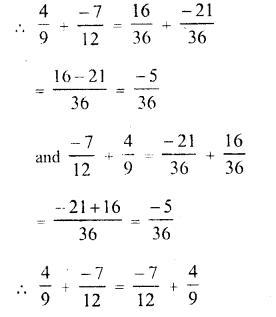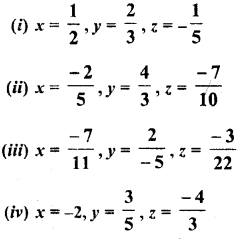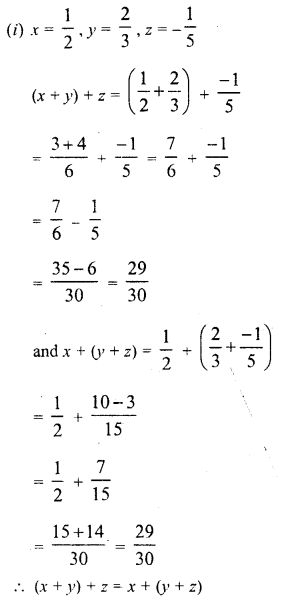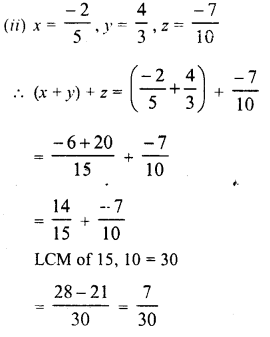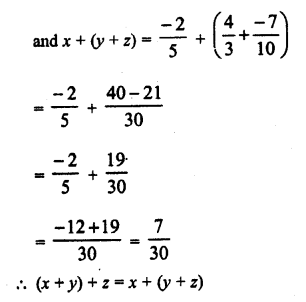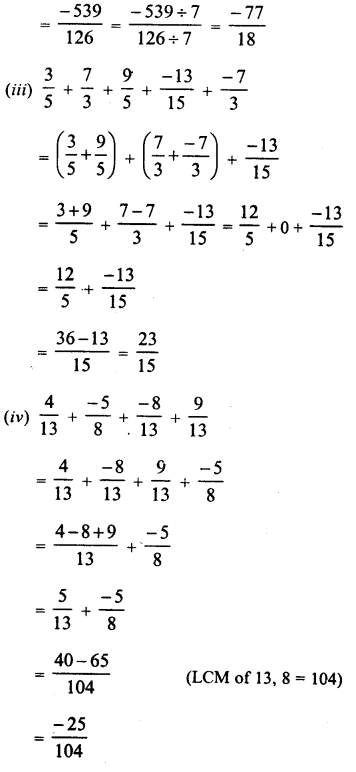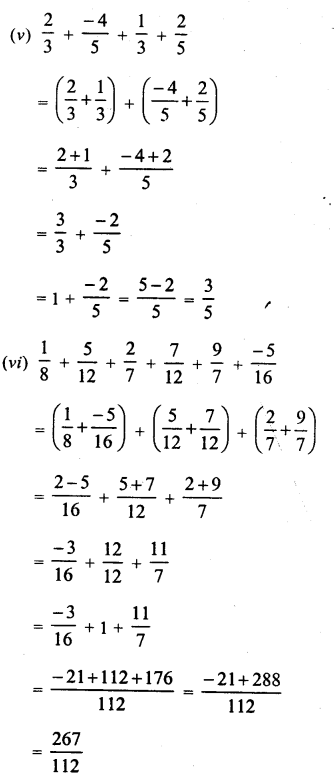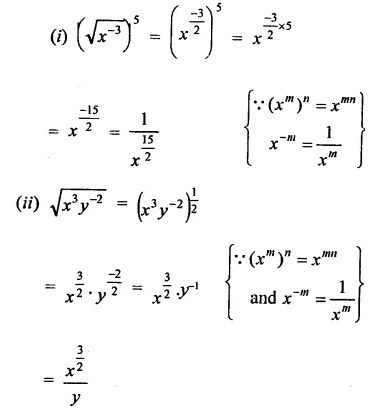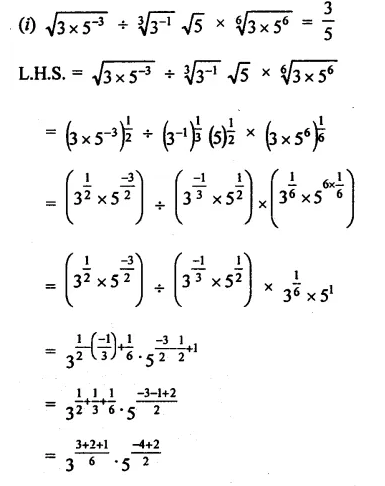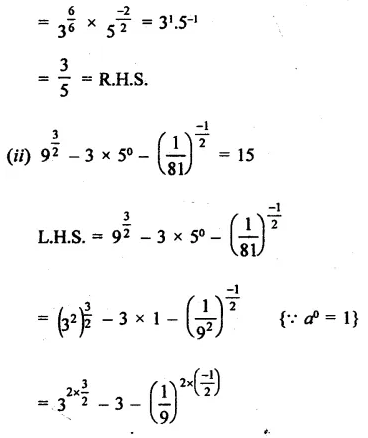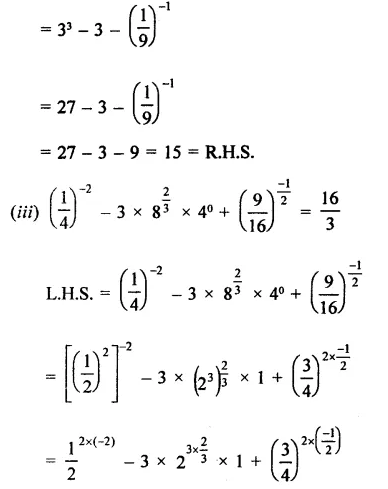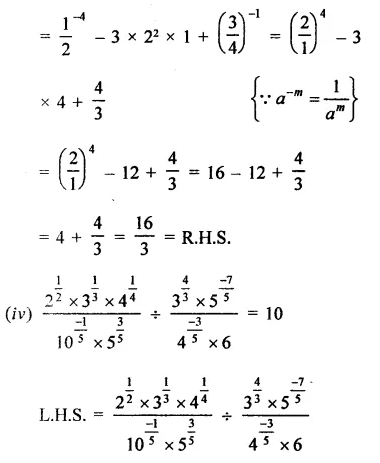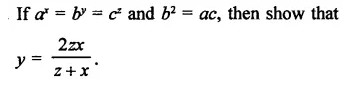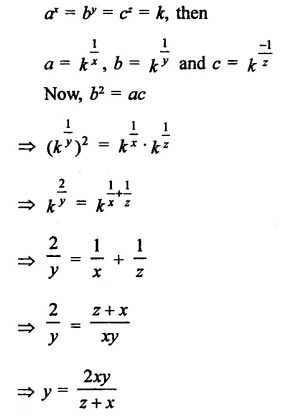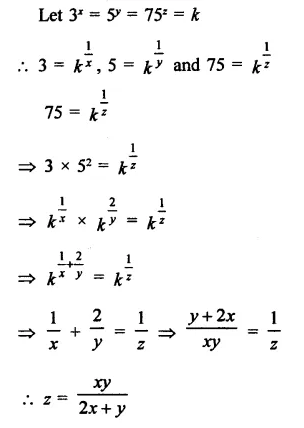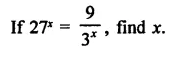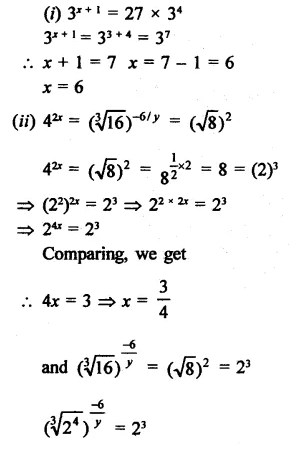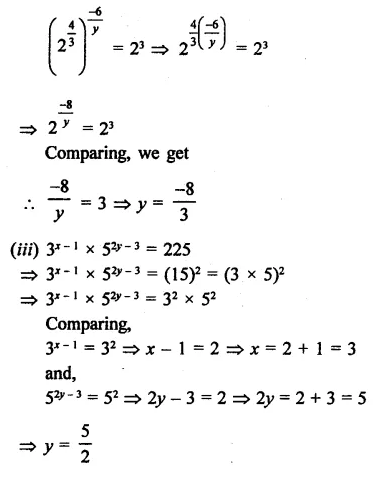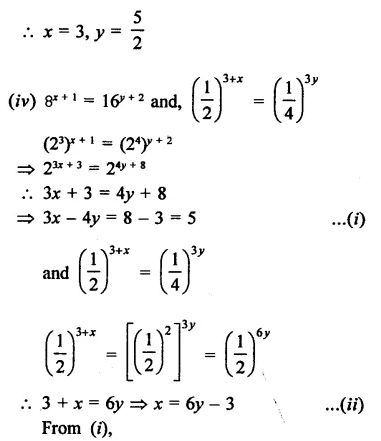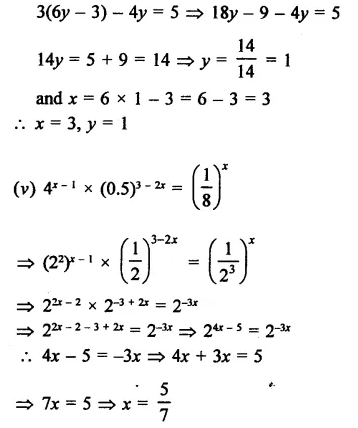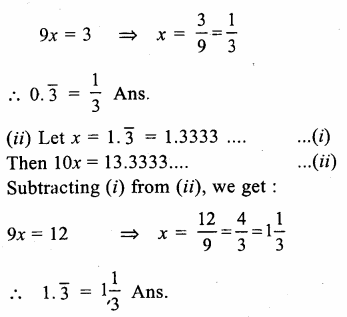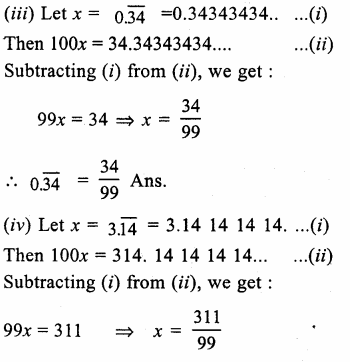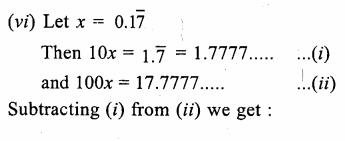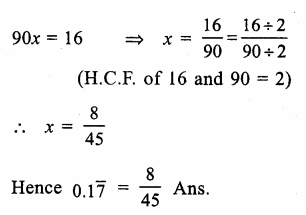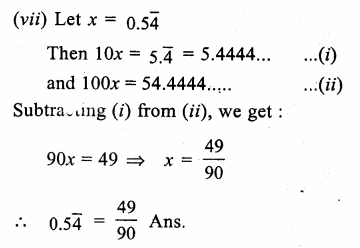Prasanna

RS Aggarwal Class 9 Solutions Chapter 1 Real Numbers Ex 1C

These Solutions are part of RS Aggarwal Solutions Class 9. Here we have given RS Aggarwal Solutions Class 9 Chapter 1 Real Numbers Ex 1C.

Other Exercises

• RS Aggarwal Solutions Class 9 Chapter 1 Real Numbers Ex 1A
• RS Aggarwal Solutions Class 9 Chapter 1 Real Numbers Ex 1B
• RS Aggarwal Solutions Class 9 Chapter 1 Real Numbers Ex 1C
• RS Aggarwal Solutions Class 9 Chapter 1 Real Numbers Ex 1D
• RS Aggarwal Solutions Class 9 Chapter 1 Real Numbers Ex 1E
• RS Aggarwal Solutions Class 9 Chapter 1 Real Numbers Ex 1F

Question 1.
Solution:
Irrational numbers : Numbers which are not rational numbers, are called irrational numbers. Rational numbers can be expressed in terminating decimals or repeating decimals while irrational number can’t.
\(\frac { 1 }{ 2 } \) , \(\frac { 2 }{ 3 } \) , \(\frac { 7 }{ 5 } \) etc.are rational numbers and π, √2, √3, √5, √6….etc are irrational numbers

Question 2.
Solution:
(i) √4 = ±2, it is a rational number
(ii) √196 = ±14 it is a rational number
(iii) √21 It is irrational number.
(iv) √43 It is irrational number.
(v) 3 + √3 It is irrational number because sum of a rational and an irrational number is irrational
(vi) √7 – 2 It is irrational number because difference of a rational and irrational number is irrational
(vii) \(\frac { 2 }{ 3 } \)√6 . It is irrational number because product of a rational and an irrational number is an irrational number.
(viii) 0.\(\overline { 6 } \) = 0.6666…. It is rational number because it is a repeating decimal.
(ix) 1.232332333…. It is irrational number because it not repeating decimal
(x) 3.040040004…. It is irrational number because it is not repeating decimal.
(xi) 3.2576 It is rational number because it is a terminating decimal.
(xii) 2.3565656…. = 2.3 \(\overline { 56 } \) It is rational number because it is a repeating decimal.
(xiii) π It is an irrational number
(xiv) \(\frac { 22 }{ 7 } \). It is a rational number which is in form of \(\frac { p }{ q } \) Ans.

Question 3.
Solution:
(i) Let X’OX be a horizontal line, taken as the x-axis and let O be the origin. Let O represent 0.
Taken OA = 1 unit and draw AB ⊥ OA such that AB = 1 unit. Join OB, Then,

Question 4.
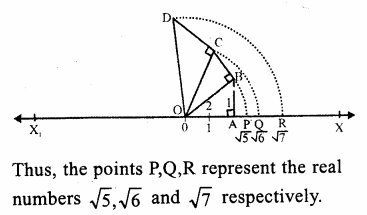
Solution:
Firstly we represent √5 on the real line X’OX. Then we will find √6 and √7 on that real line.
Now, draw a horizontal line X’OX, taken as x-axis

Question 5.
Solution:
(i) 4 + √5 : It is irrational number because in it, 4 is a rational number and √5 is irrational and sum of a rational and an irrational is also an irrational.
(ii) (-3 + √6) It is irrational number because in it, -3 is a rational and √6 is irrational and sum or difference of a rational and irrational is an irrational.
(iii) 5√7 : It is irrational because 5 is rational and √7 is irrational and product of a rational and an irrational is an irrational.
(iv) -3√8 : It is irrational because -3 is a rational and √8 is an irrational and product of a rational and an irrational is also an irrational.
(v) \(\frac { 2 }{ \sqrt { 5 } } \) It is irrational because 2 is a rational and √5 is an irrational and quotient of a rational and an irrational is also an irrational.
(vi) \(\frac { 4 }{ \sqrt { 3 } } \) It is irrational because 4 is a rational and √3 is an irrational number and quotient of a rational and irrational is also an irrational.

Question 6.
Solution:
(i) True.
(ii) False, as the sum of two irrational number is irrational is not always true.
(iii) True.
(iv) False, as the product of two irrational numbers is irrational is not always true.
(v) True.
(vi) True.
(vii) False as a real number can be either rational or irrational.

Hope given RS Aggarwal Solutions Class 9 Chapter 1 Real Numbers Ex 1C are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 10 Solutions Chapter 1 Real Numbers Ex 1D

These Solutions are part of RS Aggarwal Solutions Class 10. Here we have given RS Aggarwal Solutions Class 10 Chapter 1 Real Numbers Ex 1D. You must go through NCERT Solutions for Class 10 Maths to get better score in CBSE Board exams along with RS Aggarwal Class 10 Solutions.

Question 1.
Solution:
(i) Rational numbers: Numbers in the form of \(\frac { p }{ q }\) where p and q are integers and q ≠ 0, are called rational numbers.
(ii) Irrational numbers : The numbers which are not rationals, are called irrational numbers. Irrational numbers can be expressed in decimal form as non terminating non-repeating decimal.
(iii) Real numbers : The numbers which are rational or irrational, are called real numbers.

Question 2.
Solution:
(i) \(\frac { 22 }{ 7 }\)
It is a rational number as it is in the form of \(\frac { p }{ q }\)
(ii) 3.1416
It is a rational number as it is a terminating decimal.
(iii) π
It is an irrational number as it is nonterminating non-repeating decimal.
(iv) \(3.\bar { 142857 }\)
It is a rational number as it is nonterminating repeating decimal.
(v) 5.636363… = 5.63
It is a rational number as it is nonterminating repeating decimal.
(vi) 2.040040004…
It is an irrational number as it is nonterminating non-repeating decimal.
(vii) 1.535335333…
It is an irrational number as it is non terminating non-repeating decimal.
(viii) 3.121221222…
It is an irrational number as it is nonterminating non-repeating decimal.
(ix) √21
It is an irrational number aS it is not in the form of \(\frac { p }{ q }\)
(x) \(\sqrt [ 3 ]{ 3 }\)
It is an irrational number as it is not in the form of \(\frac { p }{ q }\)

Question 3.
Solution:
(i) √6 is irrational.
Let √6 is not an irrational number, but it is a rational number in the simplest form of \(\frac { p }{ q }\)
√6 = \(\frac { p }{ q }\) (p and q have no common factors)
Squaring both sides,
6 = \(\frac { { p }^{ 2 } }{ { q }^{ 2 } }\)
p² = 6q²
p² is divisible by 6
=> p is divisible by 6
Let p = 6a for some integer a
6q² = 36a²
=> q² = 6a²
q² is also divisible by 6
=> q is divisible by 6
6 is common factors of p and q
But this contradicts the fact that p and q have no common factor
√6 is irrational
(ii) (2 – √3) is irrational
Let (2 – √3) is a rational and 2 is also rational, then
2 – (2 – √3 ) is rational (Difference two rationals is rational)
=> 2 – 2 + √3 is rational
=> √3 is rational
But it contradicts the fact
(2 – √3) is irrational
(iii) (3 + √2 ) is irrational
Let (3 + √2 ) is rational and 3 is also rational
(3 + √2 ) – 3 is rational (Difference of two rationals is rational)
=> 3 + √2 – 3 is rational
=> √2 is rational
But it contradicts the fact (3 + √2 ) is irrational
(iv) (2 + √5 ) is irrational
Let (2 + √5 ) is rational and 2 is also rational
(2 + √5) – 2 is rational (Difference of two rationals is rational)
=> 2 + √5 – 2 is rational
=> √5 is rational
But it contradicts the fact (2 + √5) is irrational
(v) (5 + 3√2 ) is irrational
Let (5 + 3√2 ) is rational and 5 is also rational
(5 + 3√2 ) – 5 is rational (Difference of two rationals is rational)
=>5 + 3√2 – 5 is rational
=> 3√2 is rational
Product of two rationals is rational
3 is rational and √2 is rational
√2 is rational
But it contradicts the fact
(5 + 3√2 ) is irrational
(vi) 3√7 is irrational
Let 3√7 is rational
3 is rational and √7 is rational (Product of two rationals is rational)
But √7 is rational, it contradicts the fact
3√7 is irrational
(vii) \(\frac { 3 }{ \surd 5 }\) is irrational
Let \(\frac { 3 }{ \surd 5 }\) is rational
\(\frac { 3\times \surd 5 }{ \surd 5\times \surd 5 } =\frac { 3\surd 5 }{ 5 }\) is rational
\(\frac { 3 }{ 5 }\) is rational and √5 is rational
But √5 is a rational, it contradicts the fact
\(\frac { 3 }{ \surd 5 }\) is irrational
(viii)(2 – 3√5) is irrational
Let 2 – 3√5 is rational, 2 is also rational
2 – (2 – 3√5) is rational (Difference of two rationals is rational)
2 – 2 + 3√5 is rational
=> 3√5 is rational
3 is rational and √5 is rational (Product of two rationals is rational)
√5 is rational
But it contradicts the fact
(2 – 3√5) is irrational
(ix) (√3 + √5) is irrational
Let √3 + √5 is rational
Squaring,
(√3 + √5)² is rational
=> 3 x 5 + 2√3 x √5 is rational
=> 8 + 2√15 is rational
=> 8 + 2√15 – 8 is rational (Difference of two rationals is rational)
=> 2√15 is rational
2 is rational and √15 is rational (Product of two rationals is rational)
√15 is rational
But it contradicts the fact
(√3 + √5) is irrational

Question 4.
Solution:
Let \(\frac { 1 }{ \surd 3 }\) is rational
= \(\frac { 1 }{ \surd 3 } \times \frac { \surd 3 }{ \surd 3 } =\frac { \surd 3 }{ 3 } = \frac { 1 }{ 3 } \surd 3\) is rational
\(\frac { 1 }{ 3 }\) is rational and √3 is rationals (Product of two rationals is rational)
√3 is rational But it contradicts the fact
\(\frac { 1 }{ \surd 3 }\) is irrational

Question 5.
Solution:
(i) We can take two numbers 3 + √2 and 3 – √2 which are irrationals
Sum = 3 + √2 + 3 – √2 = 6 Which is rational
3 + √2 and 3 – √2 are required numbers
(ii) We take two. numbers
5 + √3 and 5 – √3 which are irrationals
Now product = (5 + √3) (5 – √3)
= (5)² – (√3 )² = 25 – 3 = 22 which is rational
5 + √3 and 5 – √3 are the required numbers

Question 6.
Solution:
(i) True.
(ii) True.
(iii) False, as sum of two irrational can be rational number also such as
(3 + √2) + (3 – √2) = 3 + √2 + 3 – √2 = 6 which is rational.
(iv) False, as product of two irrational numbers can be rational also such as
(3 + √2)(3 – √2 ) = (3)2 – (√2 )2 = 9 – 2 = 7
which is rational
(v) True.
(vi) True.

Question 7.
Solution:
Let (2√3 – 1) is a rational number and 1 is a rational number also.
Then sum = 2√3 – 1 + 1 = 2√3
In 2√3, 2 is rational and √3 is rational (Product of two rational numbers is rational)
But √3 is rational number which contradicts the fact
(2√3 – 1) is an irrational.

Question 8.
Solution:
Let 4 – 5√2 is a rational number and 4 is also a rational number
Difference of two rational number is a rational numbers
4 – (4 – 5√2 ) is rational
=> 4 – 4 + 5√2 is rational
=> 5√2 is rational
Product of two rational number is rational
5 is rational and √2 is rational
But it contradicts the fact that √2 is rational √2 is irrational
Hence, 4 – 5√2 is irrational

Question 9.
Solution:
Let (5 – 2√3) is a rational number and 5 is also a rational number
Difference of two rational number is rational
=> 5 – (5 – 2√3) is rational
=> 5 – 5 + 2√3 or 2√3 is rational
Product of two rational number is rational
2 is rational and √3 is rational
But it contradicts the fact
(5 – 2√3) is an irrational number.

Question 10.
Solution:
Let 5√2 is a rational
Product of two rationals is a rational
5 is rational and √2 is rational
But it contradicts the fact
5√2 is an irrational.

Question 11.
Solution:
\(\frac { 2 }{ \surd 7 } =\frac { 2\surd 7 }{ \surd 7\times \surd 7 } =\frac { 2\surd 7 }{ 7 } =\frac { 2 }{ 7 } \surd 7\)
Let \(\frac { 2 }{ 7 } \surd 7\) is a rational number, then
\(\frac { 2 }{ 7 }\) is rational and √7 is rational
But it contradicts the fact \(\frac { 2 }{ \surd 7 }\) is an irrational number.

Hope given RS Aggarwal Solutions Class 10 Chapter 1 Real Numbers Ex 1D are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 9 Solutions Chapter 1 Real Numbers Ex 1B

These Solutions are part of RS Aggarwal Solutions Class 9. Here we have given RS Aggarwal Solutions Class 9 Chapter 1 Real Numbers Ex 1B.

Other Exercises

• RS Aggarwal Solutions Class 9 Chapter 1 Real Numbers Ex 1A
• RS Aggarwal Solutions Class 9 Chapter 1 Real Numbers Ex 1B
• RS Aggarwal Solutions Class 9 Chapter 1 Real Numbers Ex 1C
• RS Aggarwal Solutions Class 9 Chapter 1 Real Numbers Ex 1D
• RS Aggarwal Solutions Class 9 Chapter 1 Real Numbers Ex 1E
• RS Aggarwal Solutions Class 9 Chapter 1 Real Numbers Ex 1F

Question 1.
Solution:
We know that a fraction \(\frac { p }{ q } \) is terminating if prime factors of q are 2 and 5 only.
Hence.
(i) \(\frac { 13 }{ 80 } \) and \(\frac { 16 }{ 125 } \) are the terminating decimals.

Question 2.
Solution:

Question 3.
Solution:
(i) Let,x = 0.\(\overline { 3 } \) = 0.3333…(i)
Then, 10x = 3.3333….

Question 4.
Solution:
(i) True, because set of natural numbers is a subset of whole number.
(ii) False, because the number 0 does not belong to the set of natural numbers.
(iii) True, because a set of integers is a subset of a rational numbers.
(iv) False, because the set of rational numbers is not a subset of whole numbers.
(v) True, because rational number can be expressed as terminating or repeating decimals.
(vi) True, because every rational number can be express as repeating decimals.
(vii) True, because 0 = \(\frac { 0 }{ 1 } \), which is a rational number Ans.

Hope given RS Aggarwal Solutions Class 9 Chapter 1 Real Numbers Ex 1B are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.