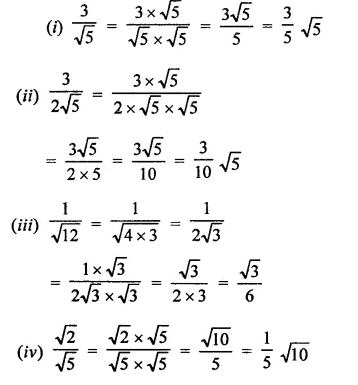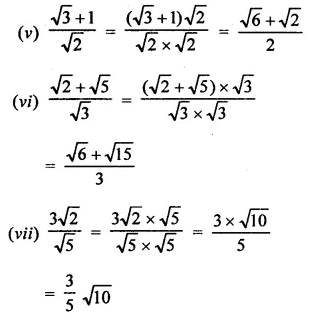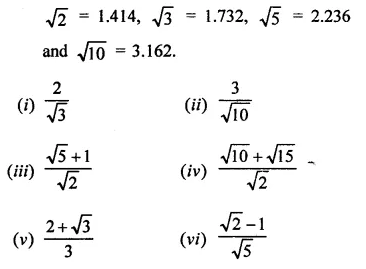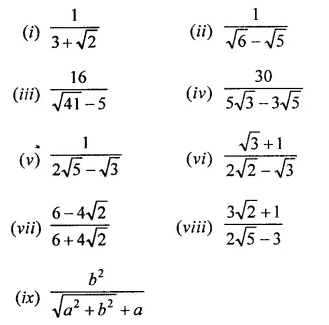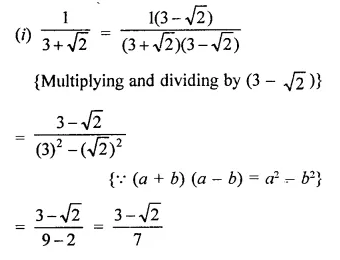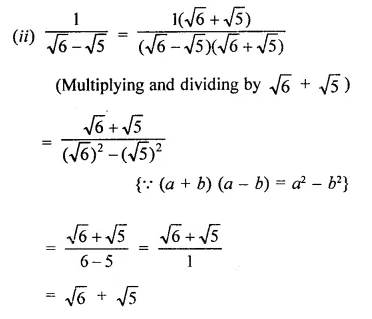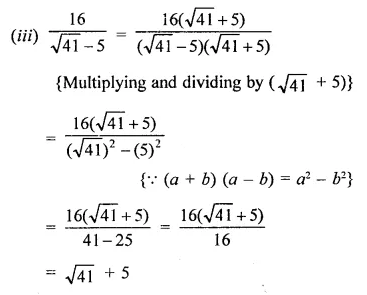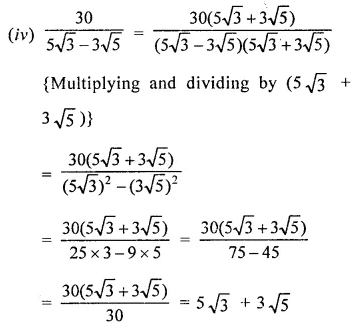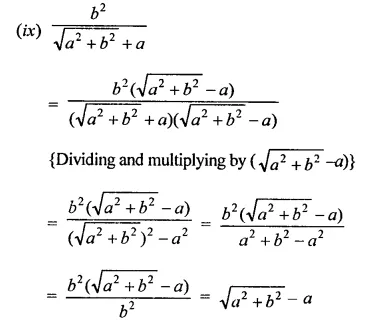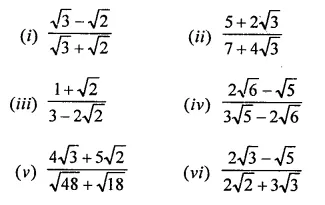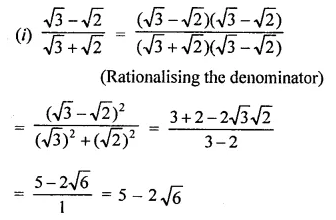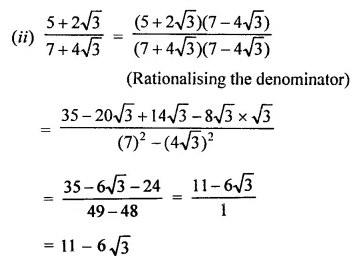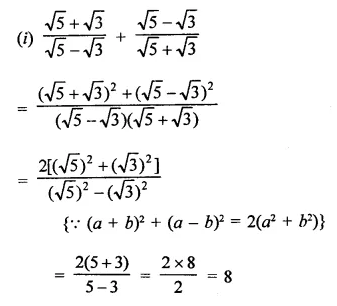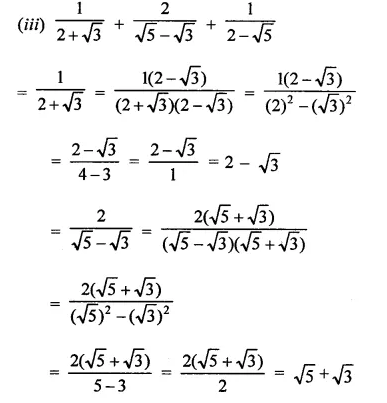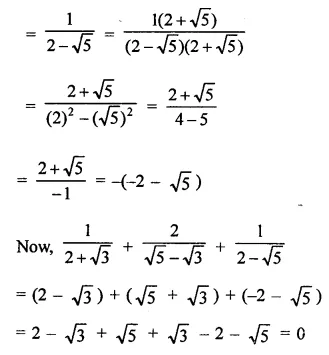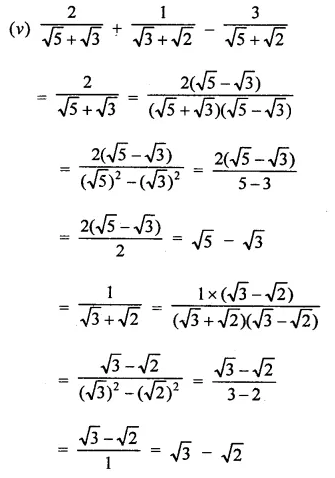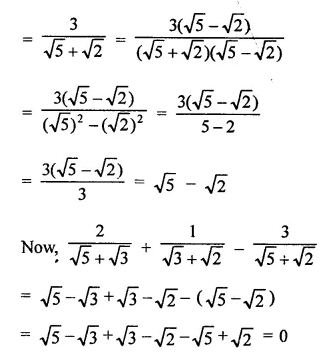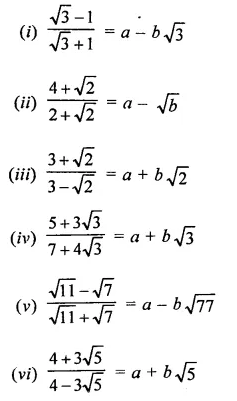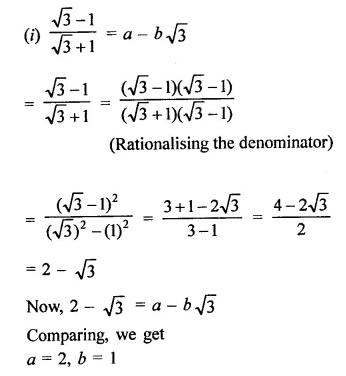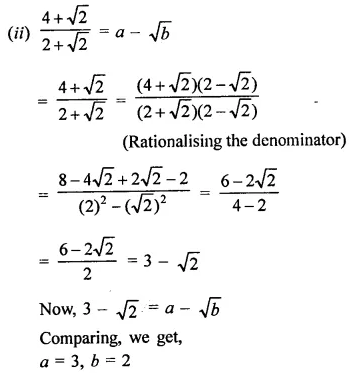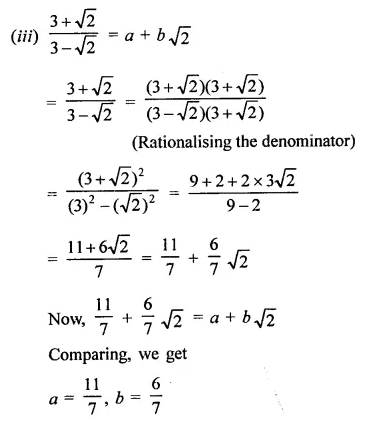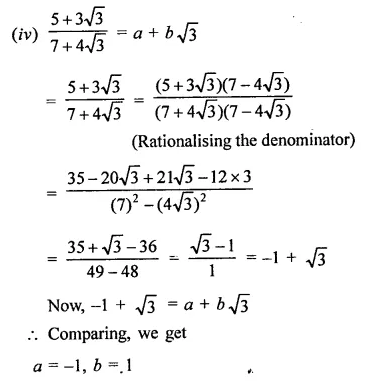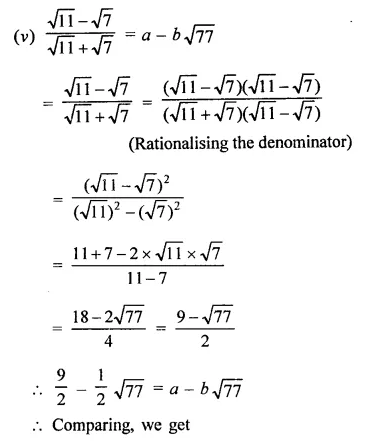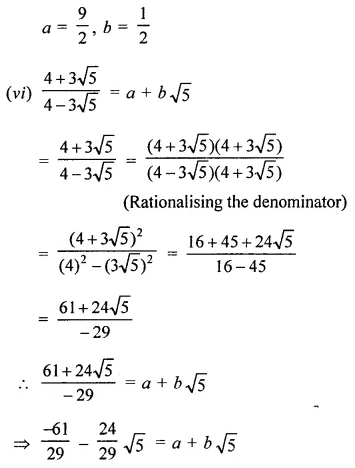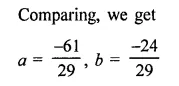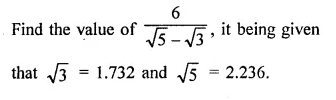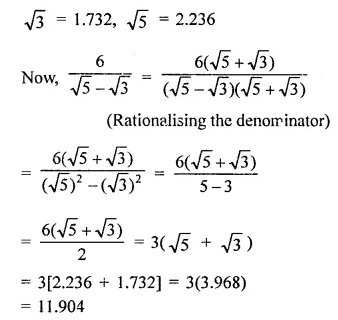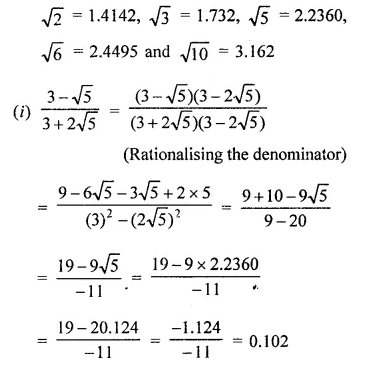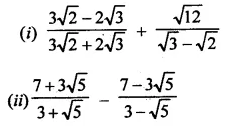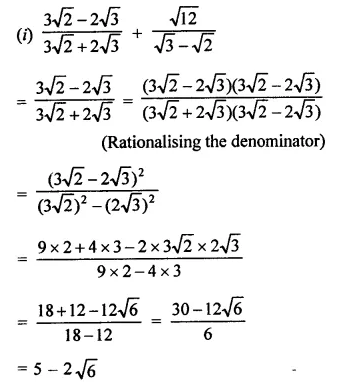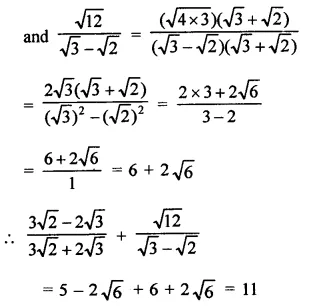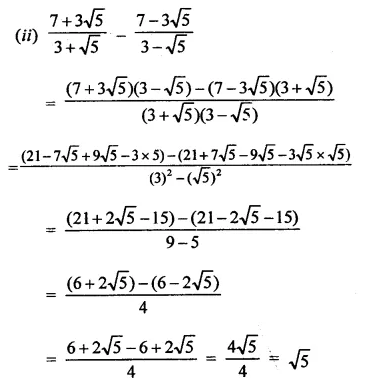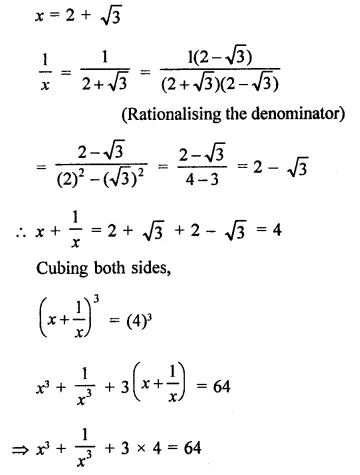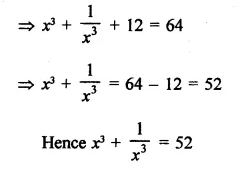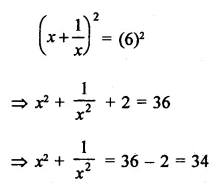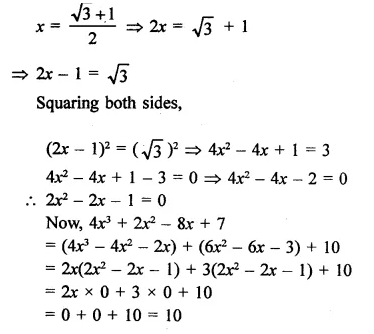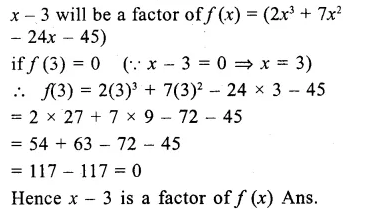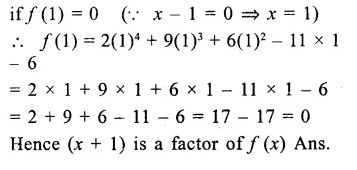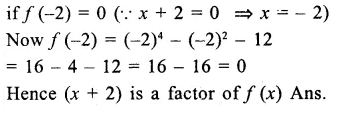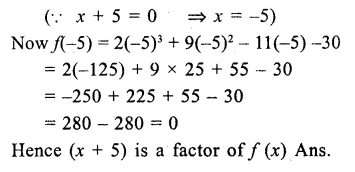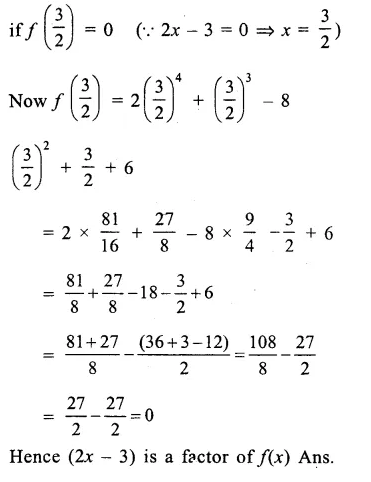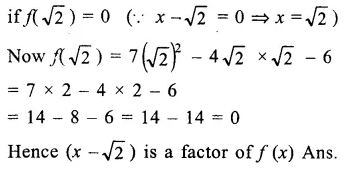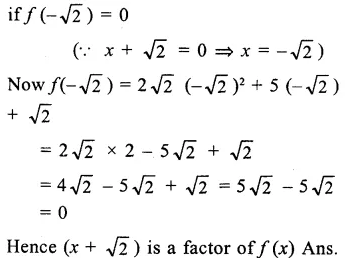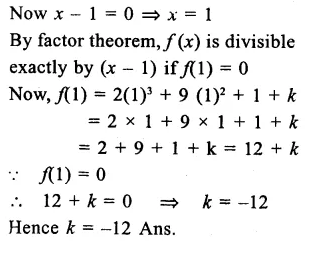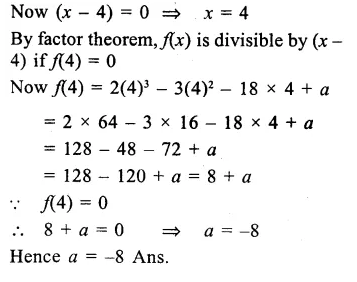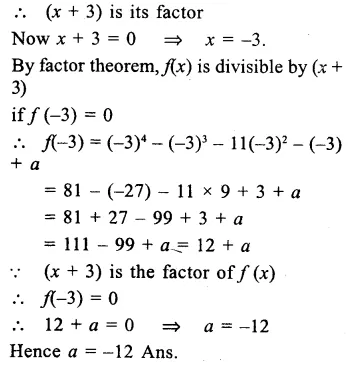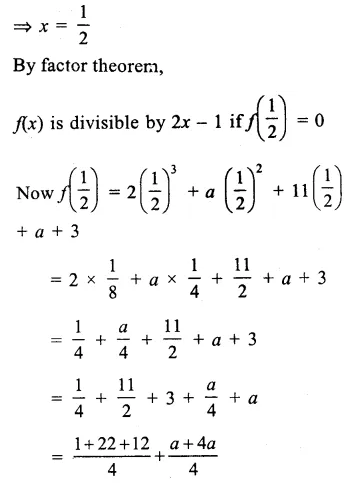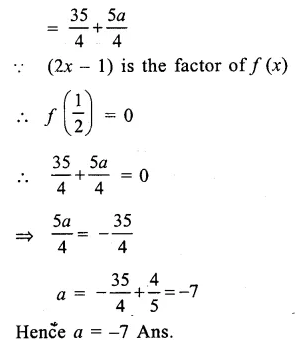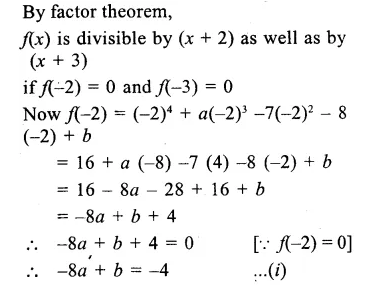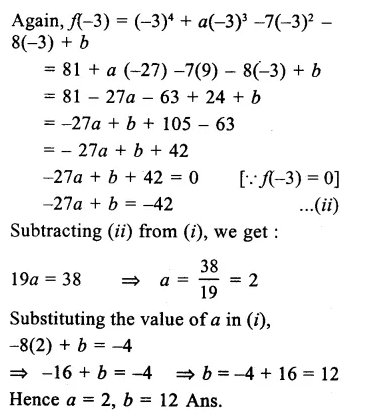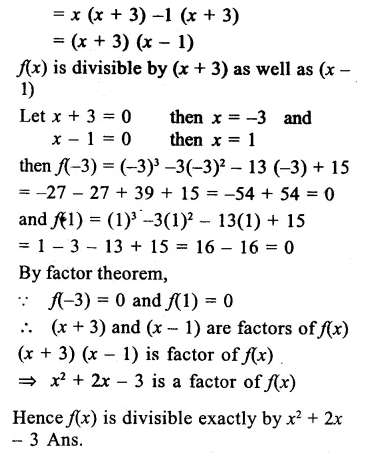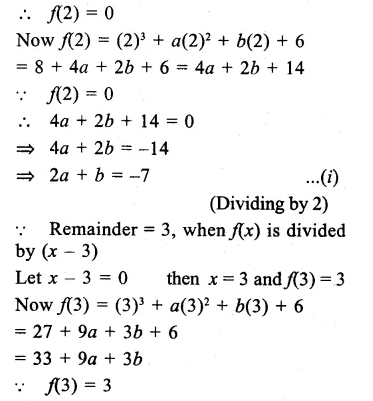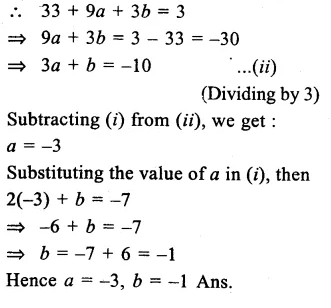Prasanna – Page 1014 – MCQ Questions

RD Sharma Class 9 Solutions Chapter 3 Rationalisation VSAQS

January 5, 2022June 18, 2018 by Prasanna

RD Sharma Class 9 Solutions Chapter 3 Rationalisation VSAQS

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 3 Rationalisation VSAQS

Question 1.
Write the value of (2 + \(\sqrt { 3 } \) ) (2 – \(\sqrt { 3 } \)).
Solution:
(2+ \(\sqrt { 3 } \) )(2- \(\sqrt { 3 } \) ) = (2)²-(\(\sqrt { 3 } \) )²{∵ (a + b) (a – b) = a² – b²}
= 4-3=1

Question 2.
Write the reciprocal of 5 + \(\sqrt { 2 } \).
Solution:
RD Sharma Class 9 Solutions Chapter 3 Rationalisation VSAQS Q2.1

Question 3.
Write the rationalisation factor of 7 – 3\(\sqrt { 5 } \) .
Solution:
Rationalising factor of 7 – 3\(\sqrt { 5 } \) is 7 + 3\(\sqrt { 5 } \)
{∵ (\(\sqrt { a } \) + \(\sqrt { b } \) ) (\(\sqrt { a } \) – \(\sqrt { b } \)) = a-b}

Question 4.
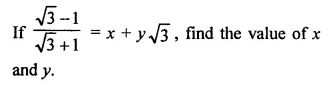
RD Sharma Class 9 Solutions Chapter 3 Rationalisation VSAQS Q4.1
Solution:

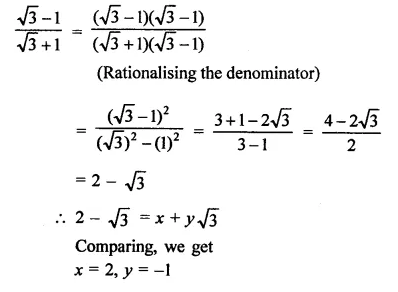
Question 5.
If x =\(\sqrt { 2 } \) – 1 then write the value of \(\frac { 1 }{ x }\).
Solution:
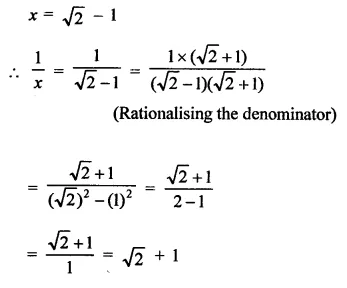
RD Sharma Class 9 Solutions Chapter 3 Rationalisation VSAQS Q5.1

Question 6.
If a = \(\sqrt { 2 } \) + h then find the value of a –\(\frac { 1 }{ a }\)
Solution:
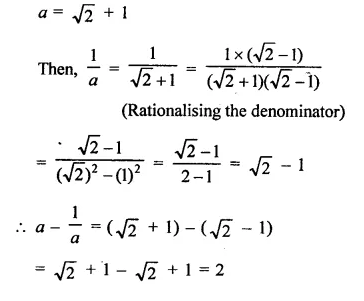
RD Sharma Class 9 Solutions Chapter 3 Rationalisation VSAQS Q6.1

Question 7.
If x = 2 + \(\sqrt { 3 } \), find the value of x + \(\frac { 1 }{ x }\).
Solution:
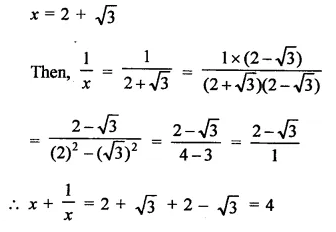
RD Sharma Class 9 Solutions Chapter 3 Rationalisation VSAQS Q7.1

Question 8.
Write the rationalisation factor of \(\sqrt { 5 } \) – 2.
Solution:
Rationalisation factor of \(\sqrt { 5 } \) – 2 is \(\sqrt { 5 } \) + 2 as
(\(\sqrt { a } \) + \(\sqrt { b } \))(\(\sqrt { a } \) – \(\sqrt { b } \)) = a – b

Question 9.
Simplify : \(\sqrt { 3+2\sqrt { 2 } }\).
Solution:
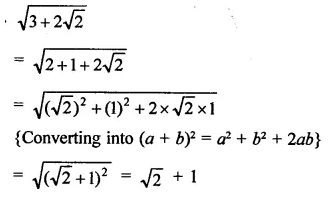
RD Sharma Class 9 Solutions Chapter 3 Rationalisation VSAQS Q9.1

Question 10.
Simplify : \(\sqrt { 3-2\sqrt { 2 } }\).
Solution:
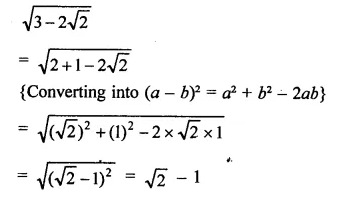
RD Sharma Class 9 Solutions Chapter 3 Rationalisation VSAQS Q10.1

Question 11.
If x = 3 + 2 \(\sqrt { 2 } \), then find the value of \(\sqrt { x } \) – \(\frac { 1 }{ \sqrt { x } }\).
Solution:
RD Sharma Class 9 Solutions Chapter 3 Rationalisation VSAQS Q11.1

Hope given RD Sharma Class 9 Solutions Chapter 3 Rationalisation VSAQS are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 8 Solutions Chapter 1 Rational Numbers Ex 1.6

January 5, 2022June 18, 2018 by Prasanna

RD Sharma Class 8 Solutions Chapter 1 Rational Numbers Ex 1.6

These Solutions are part of RD Sharma Class 8 Solutions. Here we have given RD Sharma Class 8 Solutions Chapter 1 Rational Numbers Ex 1.6

Other Exercises

Question 1.
Verify the property : x x y = y x x by taking :
RD Sharma Class 8 Solutions Chapter 1 Rational Numbers Ex 1.6 1
Solution:

Question 2.
Verify the property : x x (y x z) = (x x y) x z by taking :
RD Sharma Class 8 Solutions Chapter 1 Rational Numbers Ex 1.6 5
Solution:

Question 3.
Verify the property :xx(y + 2) = xxy + x x z by taking :
RD Sharma Class 8 Solutions Chapter 1 Rational Numbers Ex 1.6 9
Solution:

Question 4.
Use the distributivity of multiplication of rational numbers over their addition to simplify :
RD Sharma Class 8 Solutions Chapter 1 Rational Numbers Ex 1.6 11
Solution:

Question 5.
Find the multiplicative inverse (reciprocal) of each of the following rational numbers :
RD Sharma Class 8 Solutions Chapter 1 Rational Numbers Ex 1.6 14

Solution:

Question 6.
Name the property of multiplication of rational numbers illustrated by the following statements :
RD Sharma Class 8 Solutions Chapter 1 Rational Numbers Ex 1.6 18
Solution:

Question 7.
(i) The product of two positive rational numbers is always______.
(ii) The product of a positive rational number and a negative rational number is always________.
(iii) The product of two negative rational numbers is always________.
(iv) The reciprocal of a positive rational number is________.
(v) The reciprocal of a negative rational number is________.
(vi) Zero has reciprocal. The product of a rational number and its reciprocal is______.
(viii) The numbers and are their own reciprocals______.
(ix) If a is reciprocal of b, then the reciprocal of b is______.
(x) The number 0 is the reciprocal of any number______.
(xi) Reciprocal of \(\frac { 1 }{ a }\), a≠ 0 is______.
(xii) (17 x 12)^-1 = 17^-1 x________ .

Solution:
The product of two positive rational numbers is always positive.
(ii) The product of a positive rational number and a negative rational number is always negative.
(iii) The product of two negative rational numbers is always positive.
(iv) The reciprocal of a positive rational number is positive.
(v) The reciprocal of a negative rational number is negative.
(vi) Zero has no reciprocal.
(vii) The product of a rational number and its reciprocal is 1.
(viii)The numbers 1 and -1 are their own reciprocals.
(ix) If a is reciprocal of b, then the reciprocal of b is a.
(x) The number 0 is not the reciprocal of any number.
(xi) Reciprocal of \(\frac { 1 }{ a }\), a≠ 0 is a.
(xii) (17 x 12)^-1 = 17^-1 x________ .

Question 8.
Fill in the blanks :
RD Sharma Class 8 Solutions Chapter 1 Rational Numbers Ex 1.6 21

Solution:
Fill in the blanks :

Hope given RD Sharma Class 8 Solutions Chapter 1 Rational Numbers Ex 1.6 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 10 Solutions Chapter 2 Polynomials Ex 2B

January 5, 2022June 18, 2018 by Prasanna

NCERT Maths Solutions for Ex 2.2 class 10 Polynomials is the perfect guide to boost up your preparation during CBSE 10th Class Maths Examination.

RS Aggarwal Class 10 Solutions Chapter 2 Polynomials Ex 2B

These Solutions are part of RS Aggarwal Solutions Class 10. Here we have given RS Aggarwal Class 10 Solutions Chapter 2 Polynomials Ex 2B. You must go through NCERT Solutions for Class 10 Maths to get better score in CBSE Board exams along with RS Aggarwal Class 10 Solutions.

Question 1.
Solution:
Zeros are 3, -2, 1 of
p(x) = x³ – 2x² – 5x + 6
Here, a = 1, b = -2, c = -5, d = 6
We know that if α, β and γ are the roots of
f(x) = ax³ + bx² + cx + d, then
RS Aggarwal Class 10 Solutions Chapter 2 Polynomials Ex 2B 1

Question 2.
Solution:
Zeros are 5, -2 and \(\frac { 1 }{ 3 }\) of
RS Aggarwal Class 10 Solutions Chapter 2 Polynomials Ex 2B 2

Question 3.
Solution:
RS Aggarwal Class 10 Solutions Chapter 2 Polynomials Ex 2B 3

Question 4.
Solution:
RS Aggarwal Class 10 Solutions Chapter 2 Polynomials Ex 2B 4

Question 5.
Solution:
RS Aggarwal Class 10 Solutions Chapter 2 Polynomials Ex 2B 6

Find the quotient and the remainder when:
Question 6.
Solution:
RS Aggarwal Class 10 Solutions Chapter 2 Polynomials Ex 2B 7

Question 7.
Solution:
RS Aggarwal Class 10 Solutions Chapter 2 Polynomials Ex 2B 8

Question 8.
Solution:
RS Aggarwal Class 10 Solutions Chapter 2 Polynomials Ex 2B 9

Question 9.
Solution:
f(x) = 2x⁴ + 3x³ – 2x² – 9x – 12
g(x) = x² – 3
Quotient [q(x)] = 2x² + 3x + 4
Remainder [r(x)] = 0
Remainder is zero.
x² – 3 is a factor of f(x)
RS Aggarwal Class 10 Solutions Chapter 2 Polynomials Ex 2B 10

Question 10.
Solution:
RS Aggarwal Class 10 Solutions Chapter 2 Polynomials Ex 2B 11

Question 11.
Solution:
RS Aggarwal Class 10 Solutions Chapter 2 Polynomials Ex 2B 12

Question 12.
Solution:
RS Aggarwal Class 10 Solutions Chapter 2 Polynomials Ex 2B 13
= (x + 1) (x + 4) (x – 3)
If x + 4 = 0, then x = -4
If x – 3 = 0, then x = 3
Zeros are -1, -4, 3

Question 13.
Solution:
RS Aggarwal Class 10 Solutions Chapter 2 Polynomials Ex 2B 14

Question 14.
Solution:
RS Aggarwal Class 10 Solutions Chapter 2 Polynomials Ex 2B 15
=> (x – 3) (x + 3) [x (x + 2) – 1 (x + 2)]
=> (x – 3) (x + 3) (x + 2) (x – 1)
Other zeros will be
If x + 2 = 0 then x = -2
and if x – 1 =0, then x = 1
Zeros are 3, -3, -2, 1

Question 15.
Solution:
2 and -2 are the two zeros of the polynomial
f(x) = x⁴ + x³ – 34x² – 4x + 120,
Then (x – 2) (x + 2) or x² – 4 will its the factor of f(x)
Now dividing f(x) by x² – 4, we get
RS Aggarwal Class 10 Solutions Chapter 2 Polynomials Ex 2B 16
f(x) = (x – 2) (x + 2) (x² + x – 30)
= (x – 2)(x + 2)[x² + 6x – 5x – 30]
= (x – 2) (x + 2)[x(x + 6) – 5(x + 6)]
= (x – 2) (x + 2) (x + 6) (x – 5)
Other two zeros are
If x + 6 = 0, then x = -6 and
if x – 5 = 0, then x = 5
Roots of f(x) are 2, -2, -6, 5

Question 16.
Solution:
RS Aggarwal Class 10 Solutions Chapter 2 Polynomials Ex 2B 17
Other two zeros are :
if x + 5 = 0, then x = -5
and if x – 4 = 0, then x = 4
Hence, all the zeros of f(x) are : √3, – √3, 4, -5

Question 17.
Solution:
√3 and – √3 are the zeros of the polynomial
f(x) = 2x⁴ – 3x³ – 5x² + 9x – 3
=> (x – √3) (x + √3) or (x² – 3) is a factor of f(x)
Now, dividing f(x) by x² – 3, we get
RS Aggarwal Class 10 Solutions Chapter 2 Polynomials Ex 2B 18

Question 18.
Solution:
RS Aggarwal Class 10 Solutions Chapter 2 Polynomials Ex 2B 19

Question 19.
Solution:
RS Aggarwal Class 10 Solutions Chapter 2 Polynomials Ex 2B 21

Hope given RS Aggarwal Solutions Class 10 Chapter 2 Polynomials Ex 2B are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 9 Solutions Chapter 3 Rationalisation Ex 3.2

January 5, 2022June 18, 2018 by Prasanna

RD Sharma Class 9 Solutions Chapter 3 Rationalisation Ex 3.2

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 3 Rationalisation Ex 3.2

Question 1.
Rationalise the denominators of each of the following(i – vii):
RD Sharma Class 9 Solutions Chapter 3 Rationalisation Ex 3.2 Q1.1 >
Solution:

Question 2.
Find the value to three places of decimals of each of the following. It is given that
RD Sharma Class 9 Solutions Chapter 3 Rationalisation Ex 3.2 Q2.1
Solution:

Question 3.
Express each one of the following with rational denominator:
RD Sharma Class 9 Solutions Chapter 3 Rationalisation Ex 3.2 Q3.1
Solution:

Question 4.
Rationales the denominator and simplify:
RD Sharma Class 9 Solutions Chapter 3 Rationalisation Ex 3.2 Q4.1
Solution:

Question 5.
Simplify:
RD Sharma Class 9 Solutions Chapter 3 Rationalisation Ex 3.2 Q5.1
Solution:

Question 6.
In each of the following determine rational numbers a and b:
RD Sharma Class 9 Solutions Chapter 3 Rationalisation Ex 3.2 Q6.1
Solution:

Question 7.
RD Sharma Class 9 Solutions Chapter 3 Rationalisation Ex 3.2 Q7.1
Solution:

Question 8.
Find the values of each of the following correct to three places of decimals, it being given that \(\sqrt { 2 } \) = 1.4142, \(\sqrt { 3 } \) = 1-732, \(\sqrt { 5 } \) = 2.2360, \(\sqrt { 6 } \) = 2.4495 and \(\sqrt { 10 } \) = 3.162.
RD Sharma Class 9 Solutions Chapter 3 Rationalisation Ex 3.2 Q8.1
Solution:

Question 9.
Simplify:
RD Sharma Class 9 Solutions Chapter 3 Rationalisation Ex 3.2 Q9.1
Solution:

Question 10.
RD Sharma Class 9 Solutions Chapter 3 Rationalisation Ex 3.2 Q10.1
Solution:

Question 11.
RD Sharma Class 9 Solutions Chapter 3 Rationalisation Ex 3.2 Q11.1
Solution:

Question 12.
RD Sharma Class 9 Solutions Chapter 3 Rationalisation Ex 3.2 Q12.1
Solution:

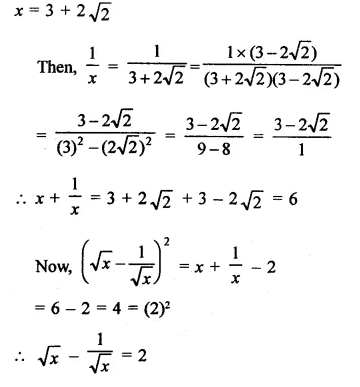
Hope given RD Sharma Class 9 Solutions Chapter 3 Rationalisation Ex 3.2 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 9 Solutions Chapter 2 Polynomials Ex 2D

January 5, 2022June 18, 2018 by Prasanna

RS Aggarwal Class 9 Solutions Chapter 2 Polynomials Ex 2D

These Solutions are part of RS Aggarwal Solutions Class 9. Here we have given RS Aggarwal Solutions Class 9 Chapter 2 Polynomials Ex 2D.

Other Exercises

Using factor theorem, show that :

Question 1.
Solution:
By factor theorem, x – 2 will be a factor of f(x) = x³ – 8 if f(2) = 0
(∴ x-2 = 0=>x = 2)
Now f(2) = (2)³ – 8 = 8- 8 = 0
Hence (x – 2) is a factor of f(x) Ans.

Question 2.
Solution:
By factor theorem,
RS Aggarwal Class 9 Solutions Chapter 2 Polynomials Ex 2D Q2.1

Question 3.
Solution:
By factor theorem,
(x – 1) is a factor of f(x)=(2x⁴ + 9x³ + 6x²– 11x – 6)
RS Aggarwal Class 9 Solutions Chapter 2 Polynomials Ex 2D Q3.1

Question 4.
Solution:
By factor theorem, (x + 2) will
a factor of f (x) = x⁴ – x⁴ + 2
RS Aggarwal Class 9 Solutions Chapter 2 Polynomials Ex 2D Q4.1

Question 5.
Solution:
By factor theorem, (x + 5) will be a factor of f(x) = 2x³ + 9x² – 11x – 30 if f(-5) = 0
RS Aggarwal Class 9 Solutions Chapter 2 Polynomials Ex 2D Q5.1

Question 6.
Solution:
By factor theorem, (2x – 3) is a factor of f(x) = 2x⁴ + x³ – 8x² – x + 6
RS Aggarwal Class 9 Solutions Chapter 2 Polynomials Ex 2D Q6.1

Question 7.
Solution:
By factor theorem, (x – √2 ) will be a factor of f(x) = 7x² – 4√2x – 6
RS Aggarwal Class 9 Solutions Chapter 2 Polynomials Ex 2D Q7.1

Question 8.
Solution:
By factor theorem, (x + √2) will be a factor of f(x) = 2√2 x³ + 5x + √2
RS Aggarwal Class 9 Solutions Chapter 2 Polynomials Ex 2D Q8.1

Question 9.
Solution:
Let f(x) = 2x³ + 9x² + x + k and x – 1 is a factor of f(x)
RS Aggarwal Class 9 Solutions Chapter 2 Polynomials Ex 2D Q9.1

Question 10.
Solution:
Let f(x) = 2x³ – 3x² – 18x + a and x – 4 is its factor
RS Aggarwal Class 9 Solutions Chapter 2 Polynomials Ex 2D Q10.1

Question 11.
Solution:
Let f(x) – x⁴ – x³ – 11x² – x + a
f(x) is divisible by (x + 3)
RS Aggarwal Class 9 Solutions Chapter 2 Polynomials Ex 2D Q11.1

Question 12.
Solution:
Let f(x) = 2x³ + ax² + 11x + a + 3
and (2x – 1) is its factor
Let 2x – 1 = 0 then 2x = 1
RS Aggarwal Class 9 Solutions Chapter 2 Polynomials Ex 2D Q12.1

Question 13.
Solution:
Let f(x) = x³ – 10x² + ax + b and (x – 1) and (x – 2) are its factors
∴ x – 1 = 0 =>x=1
and x – 2 = 2 =>x=2
RS Aggarwal Class 9 Solutions Chapter 2 Polynomials Ex 2D Q13.1

Question 14.
Solution:
Let f(x) = x⁴ + ax³ – 7x² – 8x + b ,
and (x + 2) and (x + 3) are its factors
∴x + 2 = 0 => x = -2
and x + 3= 0 => x = -3
RS Aggarwal Class 9 Solutions Chapter 2 Polynomials Ex 2D Q14.1

Question 15.
Solution:
Let f(x) = x³ – 3x² – 13x + 15
Now x² + 2x – 3 = x² + 3x – x – 3
RS Aggarwal Class 9 Solutions Chapter 2 Polynomials Ex 2D Q15.1

Question 16.
Solution:
Let f(x) = x³ + ax² + bx + 6 and (x – 2) is its factor
Let x – 2 = 0 then x = 2
RS Aggarwal Class 9 Solutions Chapter 2 Polynomials Ex 2D Q16.1

Hope given RS Aggarwal Solutions Class 9 Chapter 2 Polynomials Ex 2D are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.
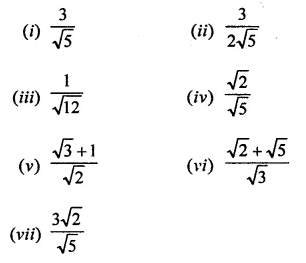