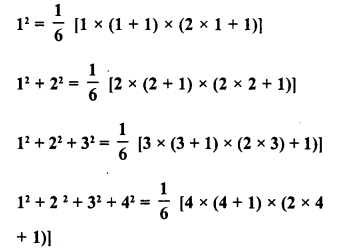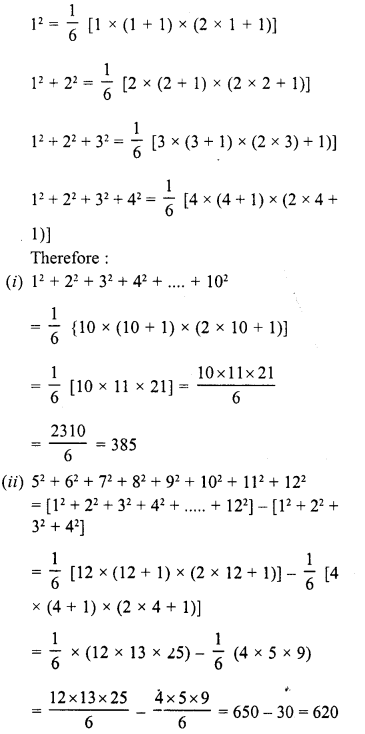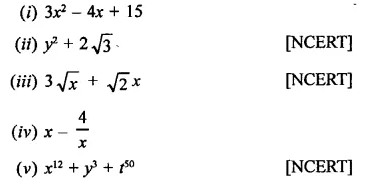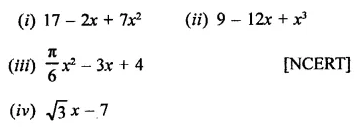Prasanna

Value Based Questions in Science for Class 9 Chapter 2 Is Matter Around Us Pure

by

Value Based Questions in Science for Class 9 Chapter 2 Is Matter Around Us Pure

These Solutions are part of Value Based Questions in Science for Class 9. Here we have given Value Based Questions in Science for Class 9 Chapter 2 Is Matter Around Us Pure

Question 1.
A student was asked by his teacher to separate an impure sample of sulphur containing sand as the impurity. He tried to purify it with the help of sublimation. But he was not successful. Particles of sulphur could not be separated completely from sand.

  1. Why did not the sublimation process succeed ?
  2. Suggest an alternate method to affect the separation.
  3. What is the value based information associated with this ?

Answer:

  1. Sulphur is not of volatile nature. Upon heating, it melts. Therefore, sublimation process could not succeed.
  2. The student should have dissolved the impure sample in carbon disulphide. It is a liquid in which sulphur completely dissolves while iron does not. From the solution, sulphur can be recovered with the help of crystallization process.
  3. The process of sublimation is useful only if one of the constituents present in the mixture can sublime while the others do not undergo sublimation.

More Resources

Question 2:
Amit was asked by his teacher to separate a liquid mixture of acetone and ethyl alcohol. He set up a distillation apparatus and tried to distil the mixture. To his surprise, both the liquids got distilled. Teacher told Amit to repeat the experiment by using a fractionating column in the distillation flask. Amit followed the advice of the teacher and he was able to separate the two liquids.

  1. Why was Amit not successful in separating the liquid mixture earlier ?
  2. Why did teacher ask him to use the fractionating column ?
  3. Which liquid was distilled first ?
  4. As a student of chemistry, what value based information you have gathered ?

Answer:

  1. The difference in boiling point temperatures of acetone (56°C) and ethyl alcohol (78°C) is only 22°C. Therefore, process of simple distillation fails in this case.
  2. Fractionating column is quite effective in this case because it obstructs the distillation of ethyl alcohol which is high boiling and at the same time helps in the distillation of acetone which is low boiling.
  3. Acetone was distilled first since it has comparatively low boiling point.
  4. The process of simple distillation can be used only in case, the liquids present in the mixture differ in their boiling point by 25°C or more.

Question 3.
A housewife got a cut on her finger while working in the Kitchen. She tried to stop the bleeding by applying dettol on it but it was not effective. By chance, her friend was also there. She asked her to rub alum on the cut which she did. The bleeding immediately stopped.

  1. Why was not dettol effective in stopping bleeding ?
  2. Why was alum effective ?
  3. What valuable service was done by the friend to the housewife ?

Answer:

  1. Blood is a colloidal solution and the colloidal particles of RBCs carry charge. Dettol is an organic compound. It could not neutralise the charge on the colloidal particles. Therefore, bleeding did not stop.
  2. Alum is a salt in which charged ions are present. When alum was applied on the cut, the charged ions neutralised the charge on the colloidal particles. In the absence of charge, blood became thick and bleeding stopped. In otherwords, blood got coagulated.
  3. The friend has a proper knowledge of colloidal solutions. She must be a student of chemistry. Timely help by her stopped the bleeding. Otherwise, there would have been a further loss of blood.

Question 4.
Mallika’s mother was suffering from cold and cough. Mallika prepared tea for her mother. She boiled water in a pan, then she added tea leaves, sugar and milk to it. She filtered the tea in a cup and served to her mother.

  1. Explain the values shown by Mallika.
  2. Identify solute, solvent, residue and filtrate in this activity. (CBSE 2013)

Answer:

  1. Mallika used the knowledge of chemistry to provide relief to her mother. Actually she prepared an extract of tea leaves which is helpful in curing cold and cough and gives warmth to the body.
  2. Solute : tea leaves and sugar ; Solvent : water and milk; Filtrate : homogeneous mixture of water, milk, sugar and extract of tea leaves.

Question 5.
Nikhil’s father was suffering from high blood pressure and cardiac problems. Doctor suggested him to take low fat milk. Nikhil churned the milk and separated the butter (fat) from it and then he served that milk to his father. Answer the following questions based on above information :

  1. Name the technique by which Nikhil separated butter from milk.
  2. Write any other application of that technique.
  3. Which values are reflected in Nikhil’s behaviour ?

Answer:

  1. It is called centrifugation carried in a centrifugal machine.
  2. Washing machines that are used for washing dirty clothes are centrifugal machines.
  3. Nikhil had the proper knowledge of chemistry. He used this to separate fat from milk with the help of the centrifugal machine. In this way, he rendered proper service to his father.

Hope given Value Based Questions in Science for Class 9 Chapter 2 Is Matter Around Us Pure are helpful to complete your science homework.

If you have any doubts, please comment below. Learn Insta try to provide online science tutoring for you.

RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.2

by

RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.2

These Solutions are part of RD Sharma Class 8 Solutions. Here we have given RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.2

Other Exercises

Question 1.
The following numbers are not perfect squares. Give reason :
(i) 1547
(ii) 45743
(iii) 8948
(iv) 333333

Solution:
We know that if the units digit is 2, 3, 7 or 8 of a number, then the number is not a perfect square.

(i) ∴ 1547 has 7 as units digit.
∴ It is not a perfect square.

(ii) 45743 has 3 as units digit
∴ It is not a perfect square.

(iii)  ∴ 8948 has 8 as units digit
∴ It is not a perfect square.

(iv)  ∴ 333333 has 3 as units digits
∴ It is not a perfect square.

Question 2.
Show that the following numbers are not perfect squares :
(i) 9327
(ii) 4058
(iii) 22453
(iv) 743522

Solution:
(i) 9327
∴ The units digit of 9327 is 7
∴ This number can’t be a perfect square.

(ii) 4058
∴ The units digit of 4058 is 8
∴ This number can’t be a perfect square.

(iii) 22453
∴ The units digit of 22453 is 3
.∴ This number can’t be a perfect square.

(iv) 743522
∴ The units digit of 743522 is 2
∴ This number can’t be a perfect square.

Question 3.
The square of which of the following numbers would be an odd number ?
(i) 731
(ii) 3456
(iii) 5559
(iv) 42008
Solution:
We know that the square of an odd number is odd and of even number is even. Therefore
(i) Square of 731 would be odd as it is an odd number.
(ii) Square of 3456 should be even as it is an even number.
(iii) Square of 5559 would be odd as it is an odd number.
(iv) The square of 42008 would be an even number as it is an even number.
Therefore suqares of (i) 731 and (ii) 5559 will be odd numbers.

Question 4.
What will be the units digit of the squares of the following numbers ?
(i) 52
(ii) 977
(iii) 4583
(iv) 78367
(v) 52698
(vi) 99880
(vii) 12796
(viii) 55555
(ix) 53924

Solution:

(i) Square of 52 will be 2704 or (2)2 = 4
∴ Its units digit is 4.

(ii) Square of 977 will be 954529 or (7)2 = 49 .
∴ Its units digit is 9

(iii) Square of 4583 will be 21003889 or (3)2 = 9
∴ Its units digit is 9

(iv) IS 78367, square of 7 = 72 = 49
∴ Its units digit is 9

(v) In 52698, square of 8 = (8)2 = 64
∴ Its units digit is 4

(vi) In 99880, square of 0 = 02 = 0
∴ Its units digit is 0

(vii) In 12796, square of 6 = 62 = 36
∴ Its units digit is 6

(viii) In In 55555, square of 5 = 52 = 25
∴ Its units digit is 5

(ix) In 53924, square pf 4 = 42 = 16
∴ Its units digit is 6

Question 5.
Observe the following pattern
1 + 3 = 22
1 + 3 + 5 = 32
1+34-5 + 7 = 42
and write the value of 1 + 3 + 5 + 7 + 9 +…………upto n terms.
Solution:
The given pattern is
1 + 3 = 22
1 + 3 + 5 = 32
1+3 + 5 + 7 = 42
1+3 + 5 + 7 + 9 +……………… upto n terms (number of terms)2 = n2

Question 6.
Observe the following pattern :
22 – 12 = 2 + 1
32 – 22 = 3 + 2
42 – 32 = 4 + 3
52 – 42 = 5 + 4
Find the value of
(i) 1002 – 992
(ii) 1112 – 1092
(iii) 992 – 962
Solution:
From the given pattern,
22 – 12 = 2 + 1
32 – 22 = 3 + 2
42 – 32 = 4 + 3
52 – 42 = 5 + 4
Therefore
(i) 1002-99° = 100 + 99

(ii) 1112 – 1092 = 1112 – 1102– 1092
= (1112 – 1102) + (1102 – 1092)
= (111 + 110) + (110+ 109)
= 221 + 219 = 440

(iii) 992 – 962 = 992 – 982 + 982 – 972 + 972 – 962
= (992 – 982) + (982 – 972) + (972 – 962)
= (99 + 98) + (98 + 97) + (97 + 96)
= 197 + 195 + 193 = 585

Question 7.
Which of the following triplets are Pythagorean ?
(i) (8, 15, 17)
(ii) (18, 80, 82)
(iii) (14, 48, 51)
(iv) (10, 24, 26)
(vi) (16, 63, 65)
(vii) (12, 35, 38)
Solution:
A pythagorean triplet is possible if (greatest number)2 = (sum of the two smaller numbers)

(i) 8, 15, 17
Here, greatest number =17
∴ (17)2 = 289
and (8)2 + (15)2 = 64 + 225 = 289
∴ 82 + 152 = 172
∴ 8, 15, 17 is a pythagorean triplet

(ii) 18, 80, 82
Greatest number = 82
∴ (82)2 = 6724
and 182 + 802 = 324 + 6400 = 6724
∴ 182 + 802 = 822
∴ 18, 80, 82 is a pythagorean triplet

(iii) 14, 48, 51
Greatest number = 51
∴ (51)2 = 2601
and 142 + 482 = 196 + 2304 = 25 00
∴ 512≠ 142 + 482
∴ 14, 48, 51 is not a pythagorean triplet

(iv) 10, 24, 26
Greatest number is 26
∴ 262 = 676
and 102 + 242 = 100 + 576 = 676
∴ 262 = 102 + 242
∴ 10, 24, 26 is a pythagorean triplet

(vi) 16, 63, 65
Greatest number = 65
∴ 652 = 4225
and 162 + 632 = 256 + 3969 = 4225
∴ 652 = 162 + 632
∴ 16, 63, 65 is a pythagorean triplet

(vii) 12, 35, 38
Greatest number = 38
∴ 382 = 1444
and 122 + 352 = 144 + 1225 = 1369
∴ 382 ≠122 + 352
∴ 12, 35, 38 is not a pythagorean triplet.

Question 8.
Observe the following pattern
RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.2 1
Solution:
From the given pattern
RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.2 2

Question 9.
Observe the following pattern
RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.2 3
and find the values of each of the following :
(i) 1 + 2 + 3 + 4 + 5 +….. + 50
(ii) 31 + 32 +… + 50
Solution:
From the given pattern,
RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.2 4

Question 10.
Observe the following pattern
RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.2 5
and find the values of each of the following :
(i) 12 + 22 + 32 + 42 +…………… + 102
(ii) 52 + 62 + 72 + 82 + 92 + 102 + 122
Solution:
From the given pattern,
RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.2 6
Question 11.
Which of the following numbers are squares of even numbers ?
121,225,256,324,1296,6561,5476,4489, 373758
Solution:
We know that squares of even numbers is also are even number. Therefore numbers 256, 324,1296, 5476 and 373758 have their units digit an even number.
∴ These are the squares of even numbers.

Question 12.
By just examining the units digits, can you tell which of the following cannot be whole squares ?

  1. 1026
  2. 1028
  3. 1024 
  4. 1022
  5. 1023
  6. 1027

Solution:
We know that a perfect square cam at ends with the digit 2, 3, 7, or 8
∴ By examining the given number, we can say that 1028, 1022, 1023, 1027 can not be perfect squares.

Question 13.
Write five numbers for which you cannot decide whether they are squares.
Solution:
A number which ends with 1,4, 5, 6, 9 or 0
can’t be a perfect square
2036, 4225, 4881, 5764, 3349, 6400

Question 14.
Write five numbers which you cannot decide whether they are square just by looking at the unit’s digit.
Solution:
A number which does not end with 2, 3, 7 or 8 can be a perfect square
∴ The five numbers can be 2024, 3036, 4069, 3021, 4900

Question 15.
Write true (T) or false (F) for the following statements.
(i) The number of digits in a square number is even.
(ii) The square of a prime number is prime.
(iii) The sum of two square numbers is a square number.
(iv) The difference of two square numbers is a square number.
(vi) The product of two square numbers is a square number.
(vii) No square number is negative.
(viii) There is not square number between 50 and 60.
(ix) There are fourteen square number upto 200. 

Solution:
(i) False : In a square number, there is no condition of even or odd digits.
(ii) False : A square of a prime is not a prime.
(iii) False : It is not necessarily.
(iv) False : It is not necessarily.
(vi) True.
(vii) True : A square is always positive.
(viii) True : As 72 = 49, and 82 = 64.
(ix) True : As squares upto 200 are 1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144, 169, 196 which are fourteen in numbers.

Hope given RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.2 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials Ex 6.1

by

RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials Ex 6.1

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials Ex 6.1

Other Exercises

Question 1.
Which of the following expressions are polynomials in one variable and which are not? State reasons for your answer:
RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials Ex 6.1 Q1.1
Solution:
(i) 3x2 – 4x + 15,
(ii) y2 + 2\(\sqrt { 3 } \) are polynomial is one variable. Others are not polynomial or polynomials in one variable.

Question 2.
Write the coefficient of x2 in each of the following:
RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials Ex 6.1 Q2.1
Solution:
Coefficient of x2,
in (i) is 7
in (ii) is 0 as there is no term of x2 i.e. 0 x2
RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials Ex 6.1 Q2.2

Question 3.
Write the degrees of each of the following polynomials:
(i) 7x3 + 4x2 – 3x + 12
(ii) 12 – x + 2x3
(iii) 5y – \(\sqrt { 2 } \)
(iv) 7
(v) 0
Solution:
(i) Degree of the polynomial 7x3 + 4x2 – 3x + 12 is 3
(ii) Degree of the polynomial 12 – x + 2x3 is 3
(iii) Degree of the polynomial 5y – \(\sqrt { 2 } \)is 1
(iv) Degree of the polynomial 7 is 0
(v) Degree of the polynomial 0 is 0 undefined.

Question 4.
Classify the following polynomials as linear, quadratic, cubic and biquadratic polynomials:
(i) x + x2 + 4
(ii) 3x – 2
(iii) 2x + x2 [NCERT]
(iv) 3y
(v) t2 + 1
(v) 7t4 + 4t3 + 3t – 2
Solution:
(i)  x + x2 + 4 It is a quadratic polynomial.
(ii) 3x – 2 : It is a linear polynomial.
(iii) 2x + x2: It is a quadratic polynomial.
(iv) 3y It is a linear polynomial.
(v) t2+ 1 It is a quadratic polynomial.
(vi) 7t4 + 4t3 + 3t – 2 It is a biquadratic polynomial.

Question 5.
Classify the following polynomials as polynomials in one-variable, two-variables etc.
(i) x2-xy +7y2
(ii) x2 – 2tx + 7t2 – x + t
(iii) t3 -3t2 + 4t-5
(iv) xy + yz + zx
Solution:
(i) x2 – xy + 7y2: It is a polynomial in two j variables x, y.
(ii) x2 – 2tx + 7t2 – x + t: It is a polynomial in two variables in x, t.
(iii) t3 – 3t2 + 4t – 5 : It is a polynomial in one variable in t.
(iv) xy +yz + zx : It is a polynomial in 3 variables in x, y and

Question 6.
Identify polynomials in the following:
RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials Ex 6.1 Q6.1
Solution:
RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials Ex 6.1 Q6.2

Question 7.
Identify constant, linear, quadratic and cubic polynomials from the following polynomials:
RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials Ex 6.1 Q7.1
Solution:
(i) f(x) = 0 : It is a constant polynomial as it has no variable.
(ii) g(x) = 2x3 – 7x + 4 : It is a cubic polynomial.
(iii) h(x) = -3x + \(\frac { 1 }{ 2 }\) : It is a linear polynomial.
(iv) p(x) = 2x2 – x + 4 : It is a quadratic polynomial.
(v) q(x) = 4x + 3 : It is linear polynomial.
(vi) r(x) = 3x3 + 4x2 + 5x – 7 : It is a cubic polynomial.

Question 8.
Give one example each of a binomial of degree 35 and of a monomial of degree 100.   [NCERT]
Solution:
Example of a binomial of degree 35 = 9x35 + 16
Example of a monomial of degree 100 = 2y100

 

Hope given RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials Ex 6.1 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

HOTS Questions for Class 9 Science Chapter 2 Is Matter Around Us Pure

by

HOTS Questions for Class 9 Science Chapter 2 Is Matter Around Us Pure

These Solutions are part of HOTS Questions for Class 9 Science. Here we have given HOTS Questions for Class 9 Science Chapter 2 Is Matter Around Us Pure.

Question 1.
A house wife churned full cream with a milk churner

  1. What will she observe after churning the milk ?
  2. What could be the possible reason for the observation ?

Answer:

  1. Churning of milk is a centrifugation process. As a result, lighter particles of cream or butter will move upwards and collect at the top. Heavier residual particles will remain at the bottom. This is a very common process used to separate cream from milk or butter from yogurt.
  2. The separation is based on the principle that lighter particles move upwards while denser particle downwards upon centrifugation.

More Resources

Question 2.
Based on separation techniques, complete the following. The first one is done for you.
HOTS Questions for Class 9 Science Chapter 2 Is Matter Around Us Pure image - 1
Answer:
2. Homogeneous, Evaporation, Difference in nature.
3. Hetereogeneous, Filtration, Difference in solubility in water
4. Homogeneous, Chromatography, Difference in adsorption of different components.

Question 3.
The table given below shows number of grams of five different solids dissolving in 100 g of the solvents : water, alcohol and chloroform (all at 20°C).
HOTS Questions for Class 9 Science Chapter 2 Is Matter Around Us Pure image - 2

  1. Which solid dissolves best in water at 20°C ?
  2. Which solid is maximum soluble in alcohol ?
  3. Which solid is insoluble in all the three solvents ?

Answer:

  1. Sugar is best soluble in water at 20°C
  2. Iodine is maximum soluble in alcohol.
  3. Chalk is insoluble in all the three solvents.

Question 4.
Some solids dissolve easily in liquids while the others donot

  1. What is the name given to the liquids which dissolve solids ?
  2. What is the name given to the clear liquid formed when a solid dissolves in a liquid ?
  3. What is the name given to the liquid which contains in it some suspended particles ?

Answer:

  1. The liquids are known as solvents
  2. The clear liquid is called solution or true solution. .
  3. The liquid is known as dispersion medium or dispersing medium.

Question 5.
Butter is an example of one type of colloidal solution. Name it. Give a reason for your choice.
Answer:
The colloidal solution is an example in which solid acts as the dispersion medium while liquid as the dispersed phase. It is also called gel.
Reason for the choice. On pressing butter, liquid drops come out of it leaving behind a solid. This clearly shows that butter is a gel.

Question 6.

  1. The solubility of sodium chloride in water increases with rise in temperature while that of lithium carbonate decreases. Assign reason.
  2. Water containing 88-8% oxygen and 11-2% hydrogen is often used as a fire extinguisher. Can a mixture containing the two gases in the same ratio by mass be used for extinguishing fire ?
  3. The melting point of a solid when determined experimentally comes out to be 160°C. But its actual melting point as given in standard books is 150°C. Predict the nature of the solid.

Answer:

  1. When sodium chloride is dissolved in water, the process is endothermic in nature. This means that heat energy is absorbed in the process. Therefore, solubility increases with rise in the temperature. In case of lithium carbonate, the process of dissolution is exothermic. This means that heat is evolved in the process. Therefore, its solubility in water decreases with rise in temperature.
  2. No, it cannot be used. Actually, in water the two elements are chemically combined with each other. They therefore, lose their identity. But in the mixture, no chemical combination between hydrogen and oxygen has taken place. Even water cannot be formed on mixing the gases. Therefore, the mixture does not extinguish any fire.
  3. Since the experimentally determined melting point of the solid is more than the standard value of the melting point, this means that the solid is not in pure state. It has some impurities present. Please note that the purity of a solid can be determined by finding its melting point and comparing it with the standard value.

Hope given HOTS Questions for Class 9 Science Chapter 2 Is Matter Around Us Pure are helpful to complete your science homework.

If you have any doubts, please comment below. Learn Insta try to provide online science tutoring for you.

RD Sharma Class 9 Solutions Chapter 5 Factorisation of Algebraic Expressions MCQS

by

RD Sharma Class 9 Solutions Chapter 5 Factorisation of Algebraic Expressions MCQS

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 5 Factorisation of Algebraic Expressions MCQS

Other Exercises

Mark the correct alternative in each of the following:
Question 1.
The factors of x3 – x2y -xy2 + y3 are
(a) (x + y) (x2 -xy + y2)
(b) (x+y)(x2 + xy + y2)
(c) (x + y)2 (x – y)
(d) (x – y)2 (x + y)
Solution:
x3 – x2y – xy2 + y3
= x3 + y3 – x2y – xy2
= (x + y) (x2 -xy + y2)- xy(x + y)
= (x + y) (x2 – xy + y2 – xy)
= (x + y) (x2 – 2xy + y2)
= (x + y) (x – y)2         (d)

Question 2.
The factors of x3 – 1 +y3 + 3xy are
(a) (x – 1 + y)  (x2 + 1 + y2 + x + y – xy)
(b) (x + y + 1)  (x2 + y2 + 1- xy – x – y)
(c) (x – 1 + y)   (x2 – 1 – y2 + x + y + xy)
(d) 3(x + y – 1) (x2 + y2 – 1)
Solution:
x3 – 1 + y3 + 3xy
= (x)3 + (-1)3 + (y)3 – 3 x  x  x (-1) x y
= (x – 1 + y) (x2 + 1 + y2 + x + y – xy)
= (x- 1 + y) (x2+ 1 + y2 + x + y – xy)      (a)

Question 3.
The factors of 8a3 + b3 – 6ab + 1 are
(a) (2a + b – 1) (4a2 + b2 + 1 – 3ab – 2a)
(b) (2a – b + 1) (4a2 + b2 – 4ab + 1 – 2a + b)
(c) (2a + b+1) (4a2 + b2 + 1 – 2ab – b – 2a)
(d) (2a – 1 + b)(4a2 + 1 – 4a – b – 2ab)
Solution:
8a3 + b3 – 6ab + 1
= (2a)3 + (b)3 + (1)3 – 3 x 2a x b x 1
= (2a + b + 1) [(2a)2 + b2+1-2a x b- b x 1 – 1 x 2a]
= (2a + b + 1) (4a2 + b2+1-2ab-b- 2a)            (c)

Question 4.
(x + y)3 – (x – v)3 can be factorized as
(a) 2y (3x2 + y2)                
(b) 2x (3x2 + y2)
(c) 2y (3y2 + x2)                
(d) 2x (x2 + 3y2)
Solution:
(x + y)3 – (x – y)3
= (x + y -x + y) [(x + y)2 + (x +y) (x -y) + (x – y)2]
= 2y(x2 + y2 + 2xy + x2-y2 + x2+y2 – 2xy)
= 2y(3x2 + y2)          (a)

Question 5.
The expression (a – b)3 + (b – c)3 + (c – a)3 can be factorized as
(a) (a -b) (b- c) (c – a) 
(b) 3(a – b) (b – c) (c – a)
(c) -3(a – b) (b – c) (a – a)
(d) (a + b + c) (a2 + b2 + c2 – ab – bc – ca)
Solution:
(a – b)3 + (b – c)3 + (c – a)3
Let a – b = x, b – a = y, c – a = z
∴ x3 + y3 + z3
x+y + z = a- b + b- c + c – a = 0
∴ x3 +y3 + z3 = 3xyz
(a – b)3 + (b – a)3 + (c – a)3
= 3 (a – b) (b – c) (c – a)        (b)

Question 6.
RD Sharma Class 9 Solutions Chapter 5 Factorisation of Algebraic Expressions MCQS Q6.1
Solution:
RD Sharma Class 9 Solutions Chapter 5 Factorisation of Algebraic Expressions MCQS Q6.2

Question 7.
RD Sharma Class 9 Solutions Chapter 5 Factorisation of Algebraic Expressions MCQS Q7.1
Solution:
RD Sharma Class 9 Solutions Chapter 5 Factorisation of Algebraic Expressions MCQS Q7.2

Question 8.
The factors of a2 – 1 – 2x – x2 are
(a) (a – x + 1) (a – x – 1)                                
(b) (a + x – 1) (a – x + 1)
(c) (a + x + 1) (a – x – 1)                               
(d) none of these
Solution:
a2 – 1- 2x – x2
⇒ a2 – (1 + 2x + x2)
= (a)2 – (1 + x)2
= (a + 1 + x) (a – 1 – x)                         (c)

Question 9.
The factors of x4 + x2 + 25 are
(a) (x2 + 3x + 5) (x2 – 3x + 5)                      
(b) (x2 + 3x + 5) (x2 + 3x – 5)
(c) (x2 + x + 5) (x2 – x + 5)                           
(d) none of these
Solution:
x4 + x2 + 25 = x4 + 25 +x2
= (x2)2 + (5)2 + 2 x x2 x 5- 9x2
= (x2 + 5)2 – (3x)2
= (x2 + 5 + 3x) (x2 + 5 – 3x)
= (x2 + 3x + 5) (x2 – 3x + 5)                 (a)

Question 10.
The factors of x2 + 4y2 + 4y – 4xy – 2x – 8 are
(a) (x – 2y – 4) (x – 2y + 2)                            
(b)  (x – y  +   2) (x – 4y – 4)
(c) (x + 2y – 4) (x + 2y + 2)                         
(d)    none of these
Solution:
x2 + 4y2 + 4y – 4xy – 2x – 8
⇒  x2 + 4y + 4y – 4xy – 2x – 8
= (x)2 + (2y)2– 2 x x x 2y + 4y-2x-8
= (x – 2y)2 – (2x – 4y) – 8
= (x – 2y)2 – 2 (x – 2y) – 8
Let x – 2y = a, then
a2– 2a – 8 = a2– 4a + 2a – 8
= a(a – 4) + 2(a – 4)
= (a-4) (a + 2)
= (x2 -2y-4) (x2 -2y + 2)                       (a)

Question 11.
The factors of x3 – 7x + 6 are
(a) x(x – 6) (x – 1)                                           
(b) (x2 – 6) (x – 1)
(c) (x + 1) (x + 2) (x – 3)                               
(d) (x – 1) (x + 3) (x – 2)
Solution:
x3 -7x + 6= x3-1-7x + 7
= (x – 1) (x2 + x + 1) – 7(x – 1)
= (x – 1) (x2 + x + 1 – 7)
= (x – 1) (x2 + x – 6)
= (x – 1) [x2 + 3x – 2x – 6]
= (x – 1) [x(x + 3) – 2(x + 3)]
= (x – 1) (x+ 3) (x – 2)                           (d)

Question 12.
The expression x4 + 4 can be factorized as
(a) (x2 + 2x + 2) (x2 – 2x + 2)                       
(b) (x2 + 2x + 2) (x2 + 2x – 2)
(c) (x2 – 2x – 2) (x2 – 2x + 2)                         
(d) (x2 + 2) (x2 – 2)
Solution:
x4 + 4 = x4 + 4 + 4x2 – 4x2                (Adding and subtracting 4x2)
= (x2)2 + (2)2 + 2 x x2 x 2 – (2x)2
= (x2 + 2)2 – (2x)2
= (x2 + 2 + 2x) (x2 + 2 – 2x)                {∵ a2 – b2 = (a + b) (a – b)}
= (x2 + 2x + 2) (x2 – 2x + 2)                  (a)

Question 13.
If 3x = a + b + c, then the value of (x – a)3 + (x –    bf + (x – cf – 3(x – a) (x – b) (x – c) is
(a) a + b + c                                                
(b) (a – b) {b – c) (c – a)
(c) 0                                                                  
(d) none of these
Solution:
3x = a + b + c                                                                      .
⇒ 3x-a-b-c = 0
Now, (x – a)3+ (x – b)3 + (x – c)3 – 3(x – a) (x -b)  (x – c)
= {(x – a) + (x – b) + (x – c)} {(x – a)2 + (x – b)2 + (x – c)2  – (x – a) (x – b) (x – b) (x – c) – (x – c) (x – a)}
= (x – a + x – b + x – c) {(x – a)2 + (x – b)2  + (x – c)2 – (x – a) (x – b) – (x – b) (x – c) – (x – c) (x – a)}
= (3x – a – b -c) {(x – a)2 + (x -b)2+ (x – c)2 – (x – a) (x – b) – (x – b) (x – c) – (x – c) (x – a)}
But 3x-a-b-c = 0, then
= 0 x {(x – a)2 + (x – b)2 + (x – c)2 – (x – a) (x – b) – (x – b) (x – c) – (x – c) (x – a)}
= 0                                                         (c)

Question 14.
If (x + y)3 – (x – y)3 – 6y(x2 – y2) = ky2, then k =
(a) 1                                   
(b) 2                                
(c) 4                                     
(d) 8
Solution:
(x + y)3 – (x – y)3 – 6y(x2 – y2) = ky2
LHS = (x + y)3 – (x – y)3 – 3 x (x + y) (x – y) [x + y – x + y]
= (x+y-x + y)3       {∵ a3 – b3 – 3ab (a – b) = a3 – b3}
= (2y)3 = 8y3
Comparing with ky3, k = 8                     (d)

Question 15.
If x3 – 3x2 + 3x – 7 = (x + 1) (ax2 + bx + c), then a + b + c =
(a) 4                                   
(b) 12                             
(c) -10                                 
(d) 3
Solution:
x3 – 3x2 + 3x + 7 = (x + 1) (ax2 + bx + c)
= ax3 + bx2 + cx + ax2 + bx + c
x3 – 3x2 + 3x – 7 = ax3 + (b + a)2 + (c + b)x + c
Comparing the coefficient,
a = 1
b + a = -3 ⇒ b+1=-3 ⇒ b = -3-1=-4
c + b = 3 ⇒ c- 4 = 3 ⇒ c = 3 + 4 = 7
a + b + c = 1- 4 + 7 = 8- 4 = 4             (a)

Hope given RD Sharma Class 9 Solutions Chapter 5 Factorisation of Algebraic Expressions MCQS are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.