RD Sharma Class 9 Solutions Chapter 5 Factorisation of Algebraic Expressions VSAQS

by

RD Sharma Class 9 Solutions Chapter 5 Factorisation of Algebraic Expressions VSAQS

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 5 Factorisation of Algebraic Expressions VSAQS

Other Exercises

Question 1.
If a + b + c = 0, then write the value of a3 + b2 + c2.
Solution:
∵ a + b + c = 0,                                                       ‘
Then a3 + b2 + c3 = 3 abc

Question 2.
If a2 + b2 + c2 = 20 and a + b + c = 0, find ab + bc + ca.
Solution:
a2 + b2 + c2 = 20, a + b + c = 0
∴ (a + b + c)2 = 0
a2 + b2 + c2 + 2(ab + bc + ca) = 0
⇒  20 + 2(ab + be + ca) = 0
⇒  2(ab + bc + ca) = -20
ab + bc + ca = \(\frac { -20 }{ 2 }\) = -10

Question 3.
If a + b + c = 9 and ab + bc + ca = 40, find a2 + b2 + c2.
Solution:
a + b + c = 9, ab + bc + ca = 40
Squaring both sides,
(a + b + c)2 = (9)2
a2 + b2 + c2 + 2{ab + bc + ca)  = 81
⇒ a2 + b2 + c2 + 2 x 40 = 81
⇒  a2 + b2 + c2 + 80 = 81
a2 + b2 + c2 = 81 – 80 = 1

Question 4.
If a2 + b2 + c2 = 250 and ab + bc + ca = 3, find a + b + c.
Solution:
a2 + b2 + c2 = 250, ab + bc + ca = 3
(a + b + c)2 = a2 + b2 + c2 + 2(ab + bc + ca)
= 250 + 2 x 3 = 250 + 6 = 256
= (±16)2
∴ a + b + c = ±16

Question 5.
Write the value of 253 – 753 + 503.
Solution:
253 – 753 + 503
Let a = 25, b = -75 and c = 50
∵  a + b + c = 25 – 75 + 50 = 0
∴ a3 + b2 + c3 = 3abc
⇒  253 + (-75)3 + 503
= 3 x 25 x (-75)- x 50 = -281250

Question 6.
Write the value of 483 – 303 – 183.
Solution:
483 – 303 – 183
Let a = 48, b = -30, c = -18
∵ a + b + c = 48 – 30 – 18 = 0
∴  a2 + b2 + c2 = 3abc
⇒  483 – 303 – 183
= 3 x 48 x (-30) (-18)
= 77760

Question 7.
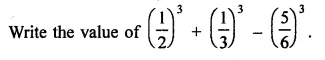
RD Sharma Class 9 Solutions Chapter 5 Factorisation of Algebraic Expressions VSAQS Q7.1
Solution:
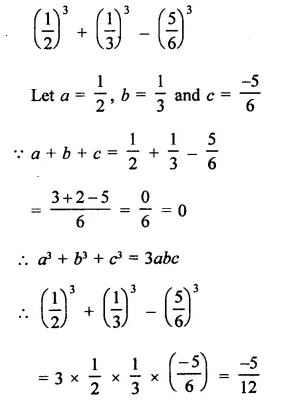
RD Sharma Class 9 Solutions Chapter 5 Factorisation of Algebraic Expressions VSAQS Q7.2

Question 8.
Write the value of 303 + 203 – 503.
Solution:
303 + 203 – 503
Let a = 30, b – 20, c = -50
∵  a + b + c = 30 + 20 -50 = 50 – 50 = 0
∴ a3 + b3 + c3 = 3 abc
⇒  303 + 203 – 503 = 3 x 30 x 20 x (-50)
= 90000

Question 9.
Factorize: x4 + x2 + 25.
Solution:
x4 + x2 + 25
⇒  (x2)2 + (5)2 + 2x2 x 5 – 2x2 x 5 +x2
⇒  (x2)2 + (5)2 + 10x2 – 10x2 + x2
= (x2)2 + (5)2 + 10x2 – 9x2
= (x2 + 5)2 – (3x)2    {∵ a2-b2 = (a + b) (a – b)}
= (x2 + 5 – 3x) (x2 + 5 + 3x)
= (x2 – 3x + 5) (x2 + 3x + 5)

Question 10.
Factorize: x2 – 1 – 2a – a2.
Solution:
x2 – 1 – 2 a – a2
= x2 – (1 +2a + a2) – (x)2 – (1 + a)2 {∵ a2 – b2 = (a + b) (a – b)}
= (x + 1 + a) (x – 1 – a)
= (x + a + 1) (x – a – 1)

Hope given RD Sharma Class 9 Solutions Chapter 5 Factorisation of Algebraic Expressions VSAQS are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.