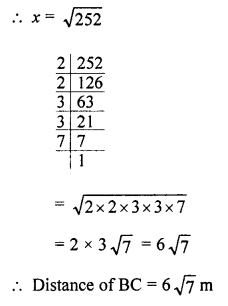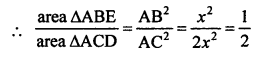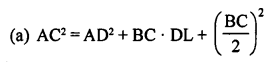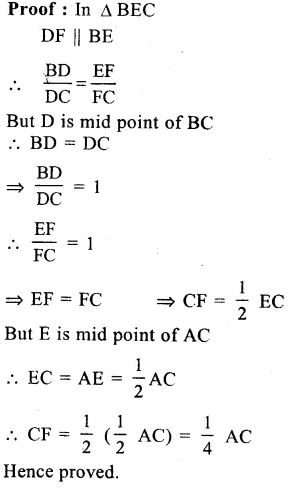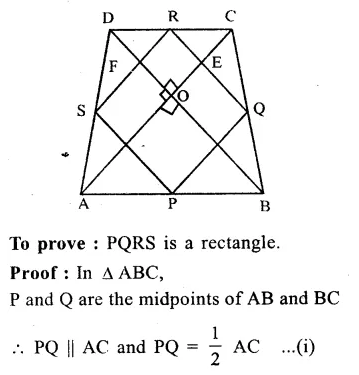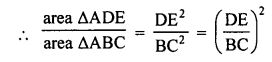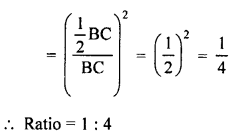Prasanna

RS Aggarwal Class 9 Solutions Chapter 10 Area Ex 10A

These Solutions are part of RS Aggarwal Solutions Class 9. Here we have given RS Aggarwal Class 9 Solutions Chapter 10 Area Ex 10A.

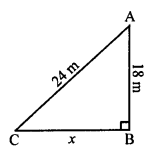
Question 1.
Solution:
Given : In the figure, ABCD is a quadrilateral and
AB = CD = 5cm

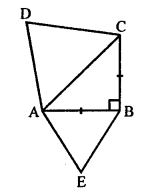
Question 2.
Solution:
In ||gm ABCD,
AB = 10cm, altitude DL = 6cm
and BM is altitude on AD, and BM = 8 cm.

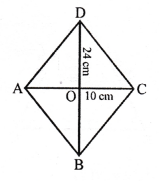
Question 3.
Solution:
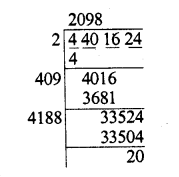
Diagonals of rhombus are 16cm and 24 cm.
Area = \(\frac { 1 }{ 2 } \) x product of diagonals
= \(\frac { 1 }{ 2 } \) x 1st diagonal x 2nd diagonal
= \(\frac { 1 }{ 2 } \) x 16 x 24
= 192 cm² Ans.

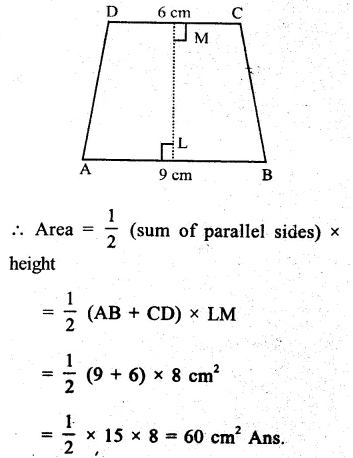
Question 4.
Solution:
Parallel sides of a trapezium are 9cm and 6cm and distance between them is 8cm

Question 5.
Solution:
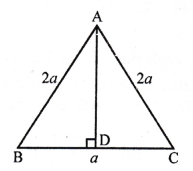
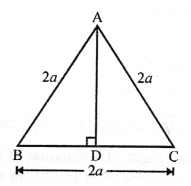
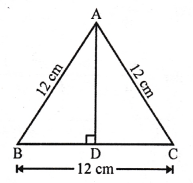
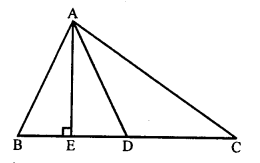
from the figure
(i) In ∆ BCD, ∠ DBC = 90°

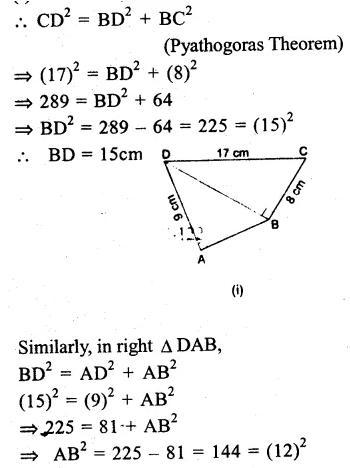
Question 6.
Solution:
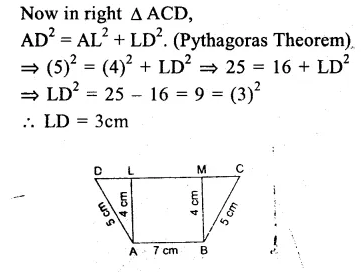
In the fig, ABCD is a trapezium. AB || DC
AB = 7cm, AD = BC = 5cm.
Distance between AB and DC = 4 cm.
i.e. ⊥AL = ⊥BM = 4cm.

Question 7.
Solution:
Given : In quad. ABCD. AL⊥BD and CM⊥BD.
To prove : ar(quad. ABCD)

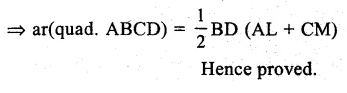
Question 8.
Solution:
In quad. ABCD, BD is its diagonal and AL⊥BD, CM⊥BD

Question 9.
Solution:
Given : ABCD is a trapezium in which AB || DC and its diagonals AC and BD intersect each other at O.
To prove : ar(∆ AOD) = ar(∆ BOC)

Question 10.
Solution:
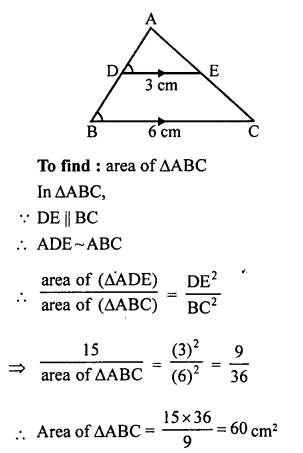
Given : In the figure,
DE || BC.

Question 11.
Solution:
Given : In ∆ ABC, D and E are the points on AB and AC such that
ar( ∆ BCE) = ar( ∆ BCD)
To prove : DE || BC.
Proof : (∆ BCE) = ar(∆ BCD)
But these are on the same base BC.
Their altitudes are equal.
Hence DE || BC
Hence proved.

Question 12.
Solution:
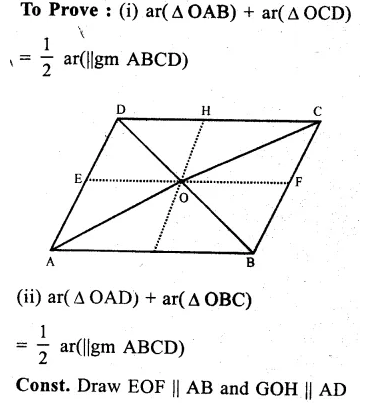
Given : In ||gm ABCD, O is any. point inside the ||gm. OA, OB, OC and OD are joined.

Question 13.
Solution:
Given : In quad. ABCD.
A line through D, parallel to AC, meets ‘BC produced in P. AP in joined which intersects CD at E.
To prove : ar( ∆ ABP) = ar(quad. ABCD).
Const. Join AC

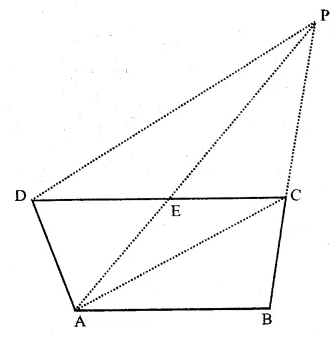
Question 14.
Solution:
Given : ∆ ABC and ∆ DBC are on the same base BC with points A and D on , opposite sides of BC and
ar( ∆ ABC) = ar( ∆ DBC).

Question 15.
Solution:
Given : In ∆ ABC, AD is the median and P is a point on AD
BP and CP are joined
To prove : (i) ar(∆BDP) = ar(∆CDP)
(ii) ar( ∆ ABP) = ar( ∆ ACP)

Question 16.
Solution:
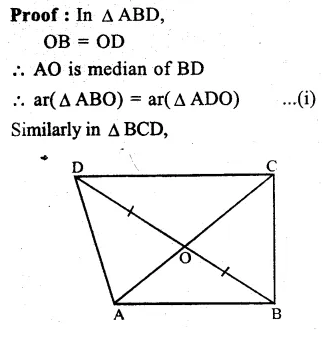
Given : In quad. ABCD, diagonals AC and BD intersect each other at O and BO = OD
To prove : ar(∆ ABC) = ar(∆ ADC)
Proof : In ∆ ABD,

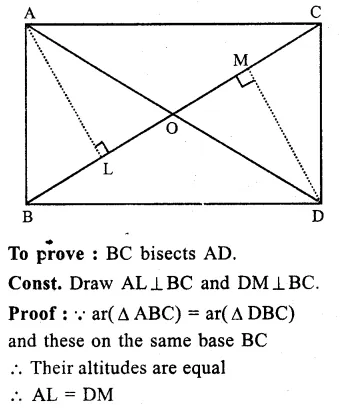
Question 17.
Solution:
In ∆ ABC,D is mid point of BC
and E is midpoint of AD and BE is joined.

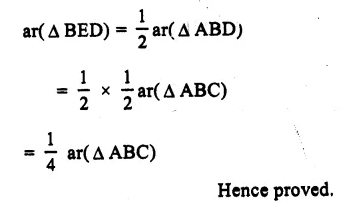
Question 18.
Solution:
Given : In ∆ ABC. D is a point on AB and AD is joined. E is mid point of AD EB and EC are joined.
To prove : ar( ∆ BEC) = \(\frac { 1 }{ 2 } \) ar( ∆ ABC)
Proof : In ∆ ABD,
E is midpoint of AD
BE is its median
ar(∆ EBD) = ar(∆ ABE)

Question 19.
Solution:
Given : In ∆ ABC, D is midpoint of BC and E is die midpoint of BO is the midpoint of AE.
To prove that ar( ∆ BOE) = \(\frac { 1 }{ 8 } \) ar(∆ ABC).

Question 20.
Solution:
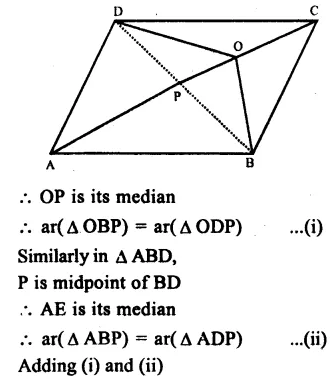
Given : In ||gm ABCD, O is any point on diagonal AC.
To prove : ar( ∆ AOB) = ar( ∆ AOD)
Const. Join BD which intersects AC at P
Proof : In ∆ OBD,
P is midpoint of BD
(Diagonals of ||gm bisect each other)

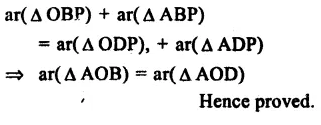
Question 21.
Solution:
Given : ABCD is a ||gm.
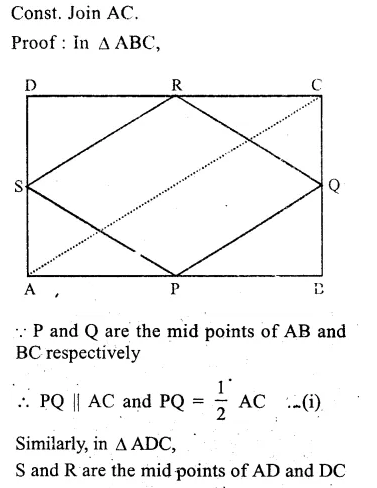
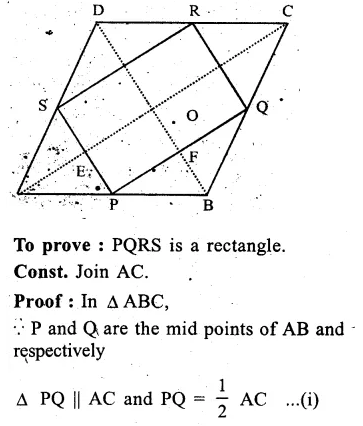
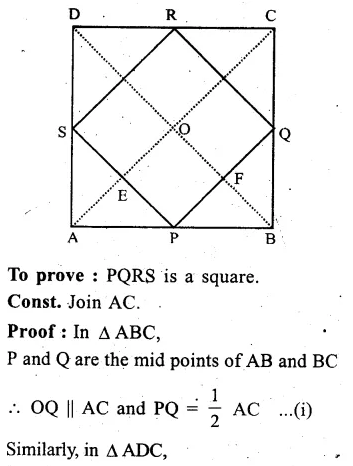
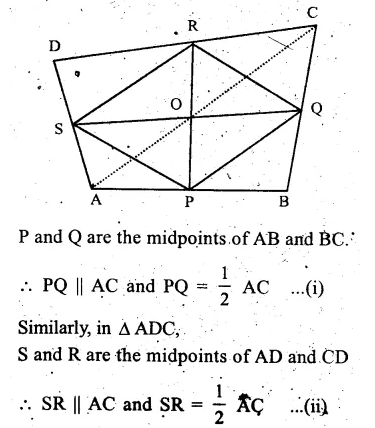
P, Q, R and S are the midpoints of sides AB, BC, CD, DA respectively.
PQ, QR, RS and SP are joined.

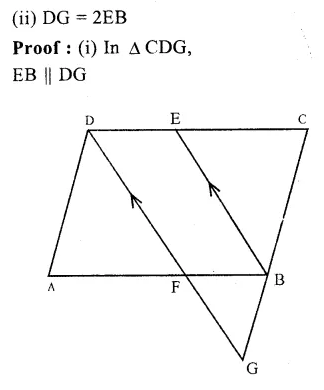
Question 22.
Solution:
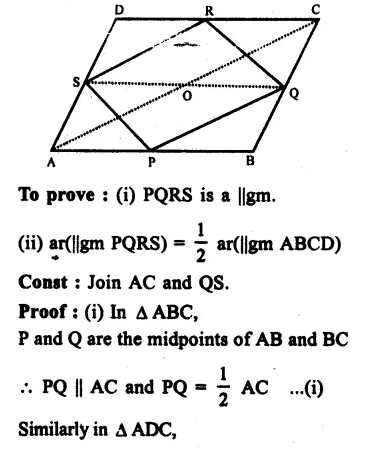
Given : In pentagon ABCDE,
EG || DA meets BA produced and
CF || DB, meets AB produced.
To prove : ar(pentagon ABCDE) = ar(∆ DGF)

Question 23.
Solution:
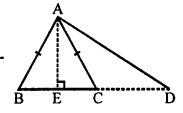
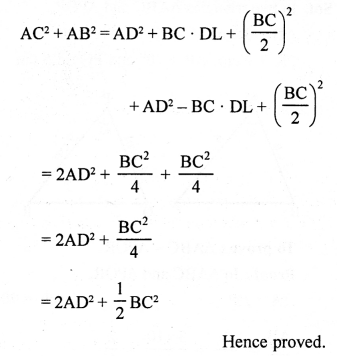
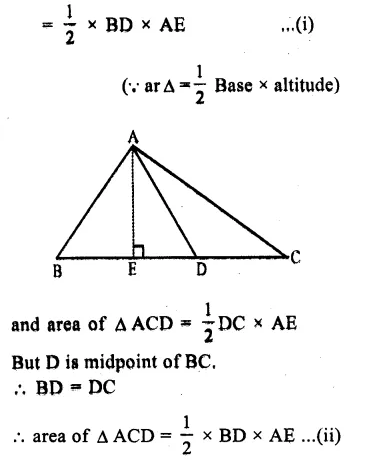
Given ; A ∆ ABC in which AD is the median.
To prove ; ar( ∆ ABD) = ar( ∆ ACD)
Const : Draw AE⊥BC.
Proof : Area of ∆ ABD

Question 24.
Solution:
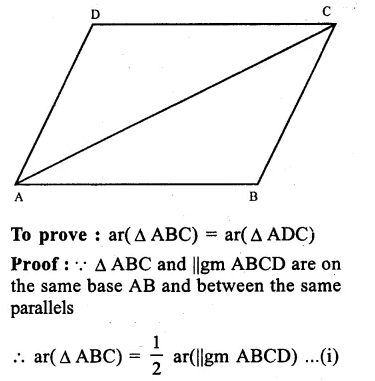
Given : A ||gm ABCD in which AC is its diagonal which divides ||gm ABCD in two ∆ ABC and ∆ ADC.

Question 25.
Solution:
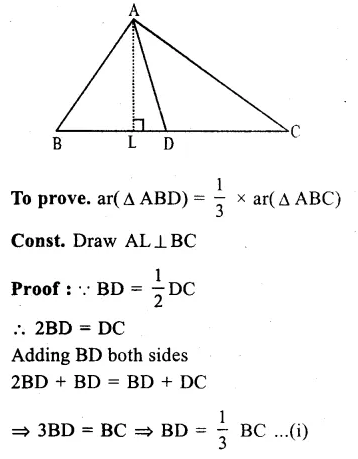
Given : In ∆ ABC,
D is a point on BC such that
BD = \(\frac { 1 }{ 2 } \) DC
AD is joined.

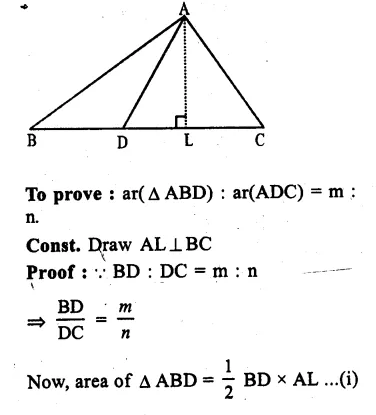
Question 26.
Solution:
Given : In ∆ ABC, D is a point on BC such that
BD : DC = m : n
AD is joined.

Hope given RS Aggarwal Class 9 Solutions Chapter 10 Area Ex 10A are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 10 Solutions Chapter 4 Triangles Ex 4D

These Solutions are part of RS Aggarwal Solutions Class 10. Here we have given RS Aggarwal Solutions Class 10 Chapter 4 Triangles Ex 4C.

Other Exercises

• RS Aggarwal Solutions Class 10 Chapter 4 Triangles Ex 4A
• RS Aggarwal Solutions Class 10 Chapter 4 Triangles Ex 4B
• RS Aggarwal Solutions Class 10 Chapter 4 Triangles Ex 4C
• RS Aggarwal Solutions Class 10 Chapter 4 Triangles Ex 4D
• RS Aggarwal Solutions Class 10 Chapter 4 Triangles Ex 4E
• RS Aggarwal Solutions Class 10 Chapter 4 Triangles MCQS
• RS Aggarwal Solutions Class 10 Chapter 4 Triangles Test Yourself

Question 1.
Solution:
For the given triangle to be right-angled, the sum of the squares of the two smaller sides must be equal to the square of the largest side.
(i) 9 cm, 16 cm, 18 cm
Longest side = 18
Now (18)² = 324
and (9)² + (16)² = 81 + 256 = 337
324 ≠ 337
It is not a right triangle.
(ii) 1 cm, 24 cm, 25 cm
Here longest side = 25 cm
(25)² = 625
and (7)² x (24)² = 49 + 576 = 625
625 = 625
It is a right triangle
(iii) 1.4 cm, 4.8 cm, 5 cm
Here longest side = 5 cm
(5)² = 25
and (1.4)² + (4.8)² = 1.96 + 23.04 = 25.00 = 25
25 = 25
It is a right triangle
(iv) 1.6 cm, 3.8 cm, 4 cm
Here longest side = 4 cm
(4 )² = 16
and (1.6)² + (3.8)² = 2.56 + 14.44 = 17.00 = 17
16 ≠ 17
It is not a right triangle
(v) (a- 1) cm, 2√a cm, (a + 1) cm
Here longest side = (a + 1) cm
(a + 1)² = a² + 2a + 1
and (a – 1)² + (2 √a )² = a² – 2a + 1 + 4a = a² + 2a + 1
a² + 2a + 1 = a² + 2a + 1
It is a right triangle.

Question 2.
Solution:
A man goes 80 m from O to east side and reaches A, then he goes 150 m due north from A and reaches B.
Join OB.

In right ∆OAB,
OB² = OA²+² (Pythagoras Theorem) = (80)² + (150)² = 6400 + 22500 = 28900
⇒ OB = √28900 = 170

He is 170 m away from the starting point.

Question 3.
Solution:
A man goes 10 m due south from O and reaches A and then 24 m due west from A and reaches B.
Join OB.

Question 4.
Solution:
Length of a ladder = 13 m
Height of the window = 12 m
Distance between the foot of the ladder and building.
In the figures,

AB is ladder, A is window of building AC
AB² = AC² + BC² (Pythagoras Theorem)
⇒ (13)² = (12)² + x²
⇒ 169 = 144 + x²
⇒ x² = 169 – 144 = 25 = (5)²
x = 5
Hence, distance between foot of ladder and building = 5 m.

Question 5.
Solution:
Let length of ladder AB = x m
Height of window AC = 20 m
and distance between the foot of the ladder and the building (BC) = 15 m

AB² = AC² + BC² (Pythagoras Theorem)
⇒ x² = 20² + 15² = 400 + 225 = 625 = (25)²
x = 25
Length of ladder = 25 m

Question 6.
Solution:
Height of first pole AB = 9 m
and of second pole CD = 14 m

Let distance between their tops CA = x m
From A, draw AE || BD meeting CD at E.
Then EA = DB = 12 m CE = CD – ED = CD – AB = 14-9 = 5 m
In right ∆AEC,
AC² = AE² + CE² = 122 + 52 = 144 + 25 = 169 = (13)²
AC = 13
Distance between their tops = 13 m

Question 7.
Solution:
Height of the pole AB = 18 m
and length of wire AC = 24 m

Distance between the base of the pole and other end of the wire
BC = x m (suppose)
In right ∆ABC,
AC² = AB² + BC² (Pythagoras Theorem)
(24)² = (18)² + x²
⇒ 576 = 324 + x²
⇒ x² = 576 – 324 = 252

Question 8.

Solution:
In ∆PQR, O is a point in it such that
OP = 6 cm, OR = 8 cm and ∠POR = 90°
PQ = 24 cm, QR = 26 cm
To prove : ∆PQR is a right angled.
In ∆POR, ∠O = 90°
PR² = PO² + OR² = (6)² + (8)² = 36 + 64 = 100 = (10)²
PR = 10
Greatest side QR is 26 cm
QR² = (26)² = 676
and PQ² + PR² = (24)² + (10)² = 576 + 100 = 676
676 = 676
QR² = PQ² + PR²
∆PQR is a right angled triangle and right angle at P.

Question 9.
Solution:
In isosceles ∆ABC, AB = AC = 13 cm
AL is altitude from A to BC
and AL = 5 cm

Now, in right ∆ALB
AB² = AL² + BL²
(13)² = (5)² + BL²
⇒ 169 = 25 + BL²
⇒ BL² = 169 – 25 = 144 = (12)²
BL = 12 cm
L is mid point of BC
BC = 2 x BC = 2 x 12 = 24 cm

Question 10.
Solution:
In an isosceles ∆ABC in which
AB = AC = 2a units, BC = a units

Question 11.
Solution:
∆ABC is an equilateral triangle
and AB = BC = CA = 2a

AD ⊥ BC
D is mid point of BC
BD = DC = \(\frac { 1 }{ 2 }\) BC
= \(\frac { 1 }{ 2 }\) x 2a = a
Now, in right ∆ADB,
AB² = AD² + BD² (Pythagoras Theorem)
(2a)² = AD² + a²
⇒ 4a² – a² = AD²
⇒ AD² = 3a² = (√3 a)²
AD = √3 a = a√3 units

Question 12.
Solution:
∆ABC is an equilateral triangle in which
AB = BC = CA = 12 cm

AD ⊥ BC which bisects BC at D
BD = DC = \(\frac { 1 }{ 2 }\) BC = \(\frac { 1 }{ 2 }\) x 12 = 6cm
Now, in right ∆ADB,
AB² = AD² + BD²
⇒ (12)² = AD² + (6)²
⇒ 144 = AD² + 36
AD² = 144 – 36 = 108
AD = √108 = √(36 x 3) = 6√3 cm

Question 13.
Solution:
Let ABCD is a rectangle in which adjacent sides.
AB = 30 cm and BC = 16 cm

AC is its diagonal.
In right ∆ABC,
AC² = AB² + BC² (Pythagoras Theorem)
= (30)² + (16)² = 900 + 256 = 1156 = (34)²
Diagonal AC = 34 cm

Question 14.
Solution:
ABCD is a rhombus
Its diagonals AC and BD bisect each other at O.

AO = OC = \(\frac { 1 }{ 2 }\) AC.
and BO = OD = \(\frac { 1 }{ 2 }\) BD
BD = 24 cm and AC = 10 cm
BO = \(\frac { 1 }{ 2 }\) x BD = \(\frac { 1 }{ 2 }\) x 24 = 12 cm
AO = \(\frac { 1 }{ 2 }\) x AC = \(\frac { 1 }{ 2 }\) x 10 = 5 cm
Now, in right ∆AOB,
AB² = AO² + BO² = (5)² + (12)² = 144 + 25 = 169 = (13)²
AB = 13
Hence, each side of rhombus = 13 cm

Question 15.
Solution:
Given : In ∆ABC, AC > AB.
D is the mid point of BC and AE ⊥ BC.
AD is joined.

To prove: AB² = AD² – BC x DE + \(\frac { 1 }{ 4 }\) BC2
Proof: In ∆AEB, ∠E = 90°
AB² = AE² + BE² …..(i) (Pythagoras Theorem)
In ∆AED, ∠E = 90°
AD² = AE² + DE²
⇒ AE² = AD² – DE² …..(ii)
Now, substitute eq. (ii) in eq. (i)
AB² = AE² + BE²
AB² = AD² – DE² + BE² [from (ii)]
AB² = (AD² – DE²) + (BD – DE)² [BE = BD – DE²]

Question 16.
Solution:

Question 17.
Solution:
Given : In ∆ABC, D is the mid point of BC, AE ⊥ BC,
BC = a, AC = b, AB = c, ED = x, AD =p and AE =
AD is joined.
To prove :

Question 18.
Solution:
Given : In ∆ABC, AB =AC
BC is produced to D and AD is joined.
To prove : (AD² – AC²) = BD x CD
Construction : Draw AE ⊥ BC.

Proof: In ∆ABC,
AB = AC and AE ⊥ BC
BE = EC
Now, in right ∆AED, ∠E = 90°
AD² = AE² + ED² …..(i)
and in right ∆AEC, ∠E = 90°
AC² = AE² + EC² …..(ii)
Now, subtracting (i) and (ii),
AD² – AC² = (AE² + ED²) – (AE² + EC²)
= AE² + ED² – AE² – EC²
= ED² – EC²
= (ED + EC) (ED – EC) (BE = EC proved above)
= BD x CD = BD x CD
AD² – AC² = BD x CD
Hence proved.

Question 19.
Solution:
Given : In ∆ABC, AB = BC and ∠ABC = 90°
∆ACD and ∆ABE are similar to each other.

To prove : Ratio between area ∆ABE and area ∆ACD.
Proof: Let AB = BC = x
Now, in right ∆ABC,
⇒ AC² = AB² + BC² = AB² + AB² = 2AB² = 2x²
∆ABE and ∆ACD are similar

Ratio between the areas of ∆ABE and ∆ACD = 1 : 2

Question 20.
Solution:
An aeroplane flies from airport to north at the speed of 1000 km/hr.
Another aeroplane flies from the airport to west at the speed of 1200 km/hr.
Period = 1\(\frac { 1 }{ 2 }\) hours
Distance covered by the first plane in 1\(\frac { 1 }{ 2 }\) hours = 1000 x \(\frac { 3 }{ 2 }\) km = 1500 km
and distance covered by another plane in 1\(\frac { 1 }{ 2 }\) hours = 1200 x \(\frac { 3 }{ 2 }\) km = 1800 km
At present, the distance between them
AB² = (BO)² + (AO)²
= (1800)² + (1500)²
= 3240000 + 2250000
= 5490000

Question 21.
Solution:
Given : In ∆ABC,
D is the mid point of BC and AL ⊥ BC
AD is joined.
To prove:

Question 22.
Solution:
AM is rod and BC is string out of rod.
In ∆BMC,
BC² = BM² + CM² = (1.8)² + (2.4)²

Hope given RS Aggarwal Solutions Class 10 Chapter 4 Triangles Ex 4D are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 9 Solutions Chapter 9 Quadrilaterals and Parallelograms Ex 9C

These Solutions are part of RS Aggarwal Solutions Class 9. Here we have given RS Aggarwal Class 9 Solutions Chapter 9 Quadrilaterals and Parallelograms Ex 9C.

Other Exercises

• RS Aggarwal Solutions Class 9 Chapter 9 Quadrilaterals and Parallelograms Ex 9A
• RS Aggarwal Solutions Class 9 Chapter 9 Quadrilaterals and Parallelograms Ex 9B
• RS Aggarwal Solutions Class 9 Chapter 9 Quadrilaterals and Parallelograms Ex 9C

Question 1.
Solution:
Given : In trapezium ABCD,
AB || DC and E is the midpoint of AD.
A line EF ||AB is drawn meeting BC at F.
To prove : F is midpoint of BC

Question 2.
Solution:
Given : In ||gm ABCD, E and F are the mid points of AB and CD respectively. A line segment GH is drawn which intersects AD, EF and BC at G, P and H respectively.
To prove : GP = PH

Question 3.
Solution:
Given : In trapezium ABCD, AB || DC
P, Q are the midpoints of sides AD and BC respectively
DQ is joined and produced to meet AB produced at E
Join AC which intersects PQ at R.

Question 4.
Solution:
Given : In ∆ ABC,
AD is the mid point of BC
DE || AB is drawn. BE is joined.
To prove : BE is the median of ∆ ABC.
Proof : In ∆ ABC

Question 5.
Solution:
Given : In ∆ ABC, AD and BE are the medians. DF || BE is drawn meeting AC at F.
To prove : CF = \(\frac { 1 }{ 4 } \) BC.

Question 6.
Solution:
Given : In ||gm ABCD, E is mid point of DC.
EB is joined and through D, DEG || EB is drawn which meets CB produced at G and cuts AB at F.
To prove : (i)AD = \(\frac { 1 }{ 2 }\) GC

Question 7.
Solution:

Given : In ∆ ABC,
D, E and F are the mid points of sides BC, CA and AB respectively
DE, EF and FD are joined.

Question 8.
Solution:
Given : In ∆ ABC, D, E and F are the mid points of sides BC, CA and AB respectively

Question 9.
Solution:
Given : In rectangle ABCD, P, Q, R and S are the midpoints of its sides AB, BC, CD and DA respectively PQ, QR, RS and SP are joined.
To prove : PQRS is a rhombus.

Question 10.
Solution:
Given : In rhombus ABCD, P, Q, R and S are the mid points of sides AB, BC, CD and DA respectively PQ, QR, RS and SP are joined.

Question 11.
Solution:
Given : In square ABCD, P,Q,R and S are the mid points of sides AB, BC, CD and DA respectively. PQ, QR, RS and SP are joined.

Question 12.
Solution:
Given : In quadrilateral ABCD, P, Q, R and S are the midpoints of PQ, QR, RS and SP respectively PR and QS are joined.
To prove : PR and QS bisect each other
Const. Join PQ, QR, RS and SP and AC
Proof : In ∆ ABC,


But diagonals of a ||gm bisect each other PR and QS bisect each other.
∴ PR and QS bisect each other

Question 13.
Solution:
Given : ABCD is a quadrilateral. Whose diagonals AC and BD intersect each other at O at right angles.
P, Q, R and S are the mid points of sides AB, BC, CD and DA respectively. PQ, QR, QS and SP are joined.

Hope given RS Aggarwal Class 9 Solutions Chapter 9 Quadrilaterals and Parallelograms Ex 9C are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 10 Solutions Chapter 4 Triangles Ex 4C

These Solutions are part of RS Aggarwal Solutions Class 10. Here we have given RS Aggarwal Solutions Class 10 Chapter 4 Triangles Ex 4C.

Other Exercises

• RS Aggarwal Solutions Class 10 Chapter 4 Triangles Ex 4A
• RS Aggarwal Solutions Class 10 Chapter 4 Triangles Ex 4B
• RS Aggarwal Solutions Class 10 Chapter 4 Triangles Ex 4C
• RS Aggarwal Solutions Class 10 Chapter 4 Triangles Ex 4D
• RS Aggarwal Solutions Class 10 Chapter 4 Triangles Ex 4E
• RS Aggarwal Solutions Class 10 Chapter 4 Triangles MCQS
• RS Aggarwal Solutions Class 10 Chapter 4 Triangles Test Yourself

Question 1.
Solution:
Given : Area of ∆ABC = 64 cm²
and area of ∆DEF =121 cm²
EF = 15.4 cm

Question 2.
Solution:

Question 3.
Solution:
∆ABC ~ ∆PQR
ar (∆ABC) = 4ar (∆PQR),

Question 4.
Solution:
Areas of two similar triangles are 169 cm² and 121 cm²
Longest side of largest triangle = 26 cm
Let longest side of smallest triangle = x
∆s are similar

Question 5.
Solution:
Area of ∆ABC = 100 cm²
and area of ∆DEF = 49 cm²

Question 6.
Solution:
Given : Corresponding altitudes of two similar triangles are 6 cm and 9 cm
We know that the areas of two similar triangles are in the ratio of the squares of their corresponding altitudes.
Ratio in the areas of two similar triangles = (6)² : (9)² = 36 : 81 = 4 : 9 (Dividing by 9)

Question 7.
Solution:
The areas of two similar triangles are 81 cm² and 49 cm²
Altitude of the first triangle = 6.3 cm
Let altitude of second triangle = x cm
The areas of two similar triangles are in the ratio of the squares on their corresponding altitude,
Let area of ∆ABC = 81 cm²
and area of ∆DEF = 49cm²
Altitude AL = 6 – 3 cm
Let altitude DM = x cm

Question 8.
Solution:
Areas of two similar triangles are 100 cm² and 64 cm²
Let area of ∆ABC = 100 cm²
and area of ∆DEF = 64 cm²
Median DM of ∆DEF = 5.6 cm
Let median AL of ∆ABC = x
The areas of two similar triangles is proportional to the squares of their corresponding median.

Question 9.
Solution:
Given : In ∆ABC, PQ is a line which meets AB in P and AC in Q.
AP = 1 cm, PB = 3 cm, AQ = 1.5 cm QC = 4.5 cm

Question 10.
Solution:
In ∆ABC,
DE || BC
DE = 3 cm, BC = 6 cm
area (∆ADE) = 15 cm²

Question 11.
Solution:
Given : In right ∆ABC, ∠A = 90°
AD ⊥ BC
BC = 13 cm, AC = 5 cm
To find : Ratio in area of ∆ABC and ∆ADC
In ∆ABC and ∆ADC
∠C = ∠C (common)
∠BAC = ∠ADC (each 90°)
∆ABC ~ ∆ADC (AA axiom)

Question 12.
Solution:
In the given figure ∆ABC,
DE || BC and DE : BC = 3 : 5.
In ∆ABC and ∆ADE,
DE || BC
∆ABC ~ ∆ADE

Question 13.
Solution:
In ∆ABC, D and E are the midpoints of sides AB and AC respectively.
DE || BC and DE = \(\frac { 1 }{ 2 }\) BC
∆ADE ~ ∆ABC

Hope given RS Aggarwal Solutions Class 10 Chapter 4 Triangles Ex 4C are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.