RD Sharma Class 9 Solutions Chapter 13 Linear Equations in Two Variables Ex 13.3
These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 13 Linear Equations in Two Variables Ex 13.3
Other Exercises
- RD Sharma Class 9 Solutions Chapter 13 Linear Equations in Two Variables Ex 13.1
- RD Sharma Class 9 Solutions Chapter 13 Linear Equations in Two Variables Ex 13.2
- RD Sharma Class 9 Solutions Chapter 13 Linear Equations in Two Variables Ex 13.3
- RD Sharma Class 9 Solutions Chapter 13 Linear Equations in Two Variables Ex 13.4
- RD Sharma Class 9 Solutions Chapter 13 Linear Equations in Two Variables VSAQS
- RD Sharma Class 9 Solutions Chapter 13 Linear Equations in Two Variables MCQS
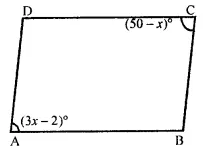
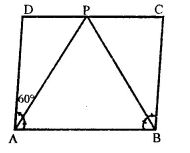
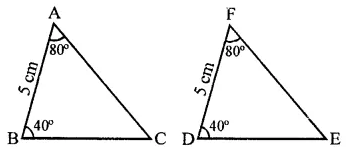
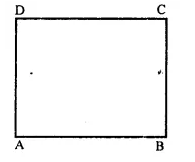
Question 1.
In a parallelogram ABCD, determine the sum of angles ZC and ZD.
Solution:
In a ||gm ABCD,
∠C + ∠D = 180°
(Sum of consecutive angles)
Question 2.
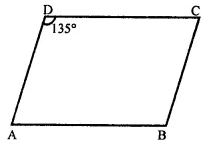
In a parallelogram ABCD, if ∠B = 135°, determine the measures of its other angles.
Solution:
In a ||gm ABCD, ∠B = 135°
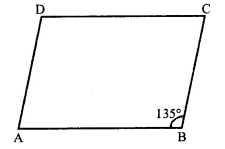
∴ ∠D = ∠B = 135° (Opposite angles of a ||gm)
But ∠A + ∠B = 180° (Sum of consecutive angles)
⇒ ∠B + 135° = 180°
∴ ∠A = 180° – 135° = 45°
But∠C = ∠B = 45° (Opposite angles of a ||gm)
∴ Angles are 45°, 135°, 45°, 135°.
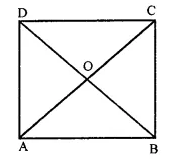
Question 3.
ABCD is a square, AC and BD intersect at O. State the measure of ∠AOB.
Solution:
In a square ABCD,
Diagonal AC and BD intersect each other at O
∵ Diagonals of a square bisect each other at right angle
∵∠AOB = 90°
Question 4.
ABCD is a rectangle with ∠ABD = 40°. Determine ∠DBC.
Solution:
In rectangle ABCD,
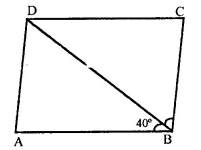
∠B = 90°, BD is its diagonal
But ∠ABD = 40°
and ∠ABD + ∠DBC = 90°
⇒ 40° + ∠DBC = 90°
⇒ ∠DBC = 90° – 40° = 50°
Hence ∠DBC = 50°
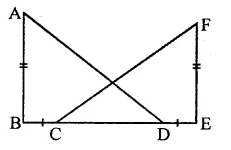
Question 5.
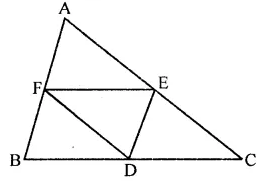
The sides AB and CD of a parallelogram ABCD are bisected at E and F. Prove that EBFD is a parallelogram.
Solution:
Given : In ||gm ABCD, E and F are the mid points of the side AB and CD respectively
DE and BF are joined
To prove : EBFD is a ||gm
Construction : Join EF
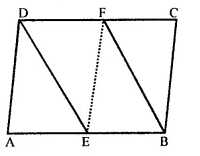
Proof : ∵ ABCD is a ||gm
∴ AB = CD and AB || CD
(Opposite sides of a ||gm are equal and parallel)
∴ EB || DF and EB = DF (∵ E and F are mid points of AB and CD)
∴ EBFD is a ||gm.
Question 6.
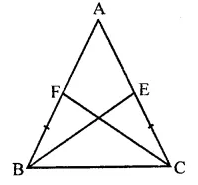
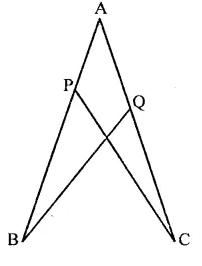
P and Q are the points of trisection of the diagonal BD of the parallelogram ABCD. Prove that CQ is parallel to AP. Prove also that AC bisects PQ.
Solution:
Given : In ||gm, ABCD. P and Q are the points of trisection of the diagonal BD
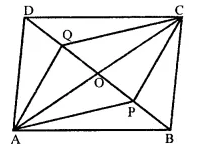
To prove : (i) CQ || AP
AC bisects PQ
Proof: ∵ Diagonals of a parallelogram bisect each other
∴ AO = OC and BO = OD
∴ P and Q are point of trisection of BD
∴ BP = PQ = QD …(i)
∵ BO = OD and BP = QD …(ii)
Subtracting, (ii) from (i) we get
OB – BP = OD – QD
⇒ OP = OQ
In quadrilateral APCQ,
OA = OC and OP = OQ (proved)
Diagonals AC and PQ bisect each other at O
∴ APCQ is a parallelogram
Hence AP || CQ.
Question 7.
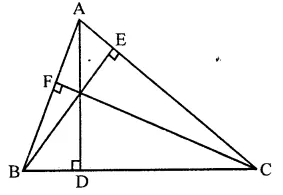
ABCD is a square. E, F, G and H are points on AB, BC, CD and DA respectively, such that AE = BF = CG = DH. Prove that EFGH is a square.
Solution:
Given : In square ABCD
E, F, G and H are the points on AB, BC, CD and DA respectively such that AE = BF = CG = DH
To prove : EFGH is a square
Proof : E, F, G and H are points on the sides AB, BC, CA and DA respectively such that
AE = BF = CG = DH = x (suppose)
Then BE = CF = DG = AH = y (suppose)
Now in ∆AEH and ∆BFE
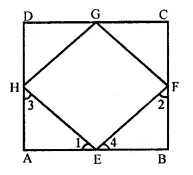
AE = BF (given)
∠A = ∠B (each 90°)
AH = BE (proved)
∴ ∆AEH ≅ ∆BFE (SAS criterion)
∴ ∠1 = ∠2 and ∠3 = ∠4 (c.p.c.t.)
But ∠1 + ∠3 = 90° and ∠2 + ∠4 = 90° (∠A = ∠B = 90°)
⇒ ∠1 + ∠2 + ∠3 + ∠4 = 90° + 90° = 180°
⇒ ∠1 + ∠4 + ∠1 + ∠4 = 180°
⇒ 2(∠1 + ∠4) = 180°
⇒ ∠1 + ∠4 = \(\frac { { 180 }^{ \circ } }{ 2 }\) = 90°
∴ ∠HEF = 180° – 90° = 90°
Similarly, we can prove that
∠F = ∠G = ∠H = 90°
Since sides of quad. EFGH is are equal and each angle is of 90°
∴ EFGH is a square.
Question 8.
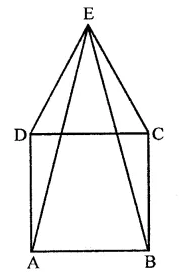
ABCD is a rhombus, EABF is a straight line such that EA = AB = BF. Prove that ED and FC when produced meet at right angles.
Solution:
Given : ABCD is a rhombus, EABF is a straight line such that
EA = AB = BF
ED and FC are joined
Which meet at G on producing
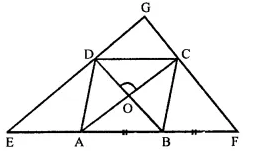
To prove: ∠EGF = 90°
Proof : ∵ Diagonals of a rhombus bisect
each other at right angles
AO = OC, BO = OD
∠AOD = ∠COD = 90°
and ∠AOB = ∠BOC = 90°
In ∆BDE,
A and O are the mid-points of BE and BD respectively.
∴ AO || ED
Similarly, OC || DG
In ∆ CFA, B and O are the mid-points of AF and AC respectively
∴ OB || CF and OD || GC
Now in quad. DOCG
OC || DG and OD || CG
∴ DOCG is a parallelogram.
∴ ∠DGC = ∠DOC (opposite angles of ||gm)
∴ ∠DGC = 90° (∵ ∠DOC = 90°)
Hence proved.
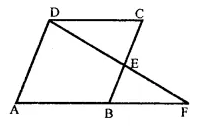
Question 9.
ABCD is a parallelogram, AD is produced to E so that DE = DC = AD and EC produced meets AB produced in F. Prove that BF = BC.
Solution:
Given : In ||gm ABCD,
AB is produced to E so that
DE = DA and EC produced meets AB produced in F.
To prove : BF = BC
Proof: In ∆ACE,
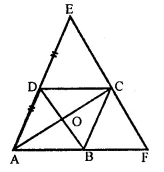
O and D are the mid points of sides AC and AE
∴ DO || EC and DB || FC
⇒ BD || EF
∴ AB = BF
But AB = DC (Opposite sides of ||gm)
∴ DC = BF
Now in ∆EDC and ∆CBF,
DC = BF (proved)
∠EDC = ∠CBF
(∵∠EDC = ∠DAB corresponding angles)
∠DAB = ∠CBF (corresponding angles)
∠ECD = ∠CFB (corresponding angles)
∴ AEDC ≅ ACBF (ASA criterion)
∴ DE = BC (c.p.c.t.)
⇒ DC = BC
⇒ AB = BC
⇒ BF = BC (∵AB = BF proved)
Hence proved.
Hope given RD Sharma Class 9 Solutions Chapter 13 Linear Equations in Two Variables Ex 13.3 are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.