RD Sharma Class 9 Solutions Chapter 13 Linear Equations in Two Variables VSAQS
These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 13 Linear Equations in Two Variables VSAQS
Other Exercises
- RD Sharma Class 9 Solutions Chapter 13 Linear Equations in Two Variables Ex 13.1
- RD Sharma Class 9 Solutions Chapter 13 Linear Equations in Two Variables Ex 13.2
- RD Sharma Class 9 Solutions Chapter 13 Linear Equations in Two Variables Ex 13.3
- RD Sharma Class 9 Solutions Chapter 13 Linear Equations in Two Variables Ex 13.4
- RD Sharma Class 9 Solutions Chapter 13 Linear Equations in Two Variables VSAQS
- RD Sharma Class 9 Solutions Chapter 13 Linear Equations in Two Variables MCQS
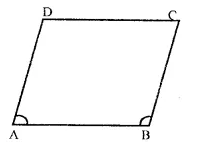
Question 1.
In a parallelogram ABCD, write the sum of angles A and B.
Solution:
In ||gm ABCD,
∠A + ∠B = 180°
(Sum of consecutive angles of a ||gm)
Question 2.
In a parallelogram ABCD, if ∠D = 115°, then write the measure of ∠A.
Solution:
In ||gm ABCD,
∠D = 115°
But ∠A + ∠D = 180°
(Sum of consecutive angles of a ||gm)
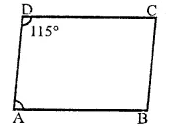
⇒ ∠A + 115°= 180° ∠A = 180°- 115°
∴ ∠A = 65°
Question 3.
PQRS is a square such that PR and SQ intersect at O. State the measure of ∠POQ.
Solution:
In a square PQRS,
Diagonals PR and QS intersects each other at O.
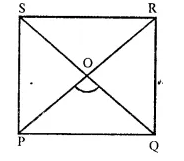
∵ The diagonals of a square bisect each other at right angles.
∴ ∠POQ = 90°
Question 4.
If PQRS is a square then write the measure of ∠SRP.
Solution:
In square PQRS,
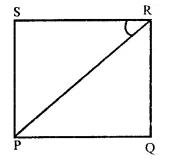
Join PR,
∵Diagonals of a square bisect are opposite angles
∴∠SRP = \(\frac { 1 }{ 2 }\)x ∠SRQ
= \(\frac { 1 }{ 2 }\) x 90° = 45°
Question 5.
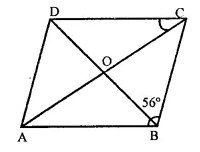
If ABCD is a rhombus with ∠ABC = 56°, find the measure of ∠ACD.
Solution:
In rhombus ABCD,
Diagonals bisect each other at 0 at right angles.
∠ABC = 56°
But ∠ABC + ∠BCD = 180° (Sum of consecutive angles)
⇒ 56° + ∠BCD = 180°
⇒ ∠BCD = 180° – 56° = 124°
∵ Diagonals of a rhombus bisect the opposite angle
∴ ∠ACD = \(\frac { 1 }{ 2 }\) ∠BCD = \(\frac { 1 }{ 2 }\) x 124°
= 62°
Question 6.
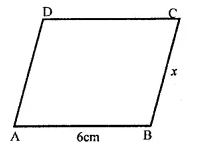
The perimeter of a parallelogram is 22 cm. If the longer side measures 6.5 cm, what is the measure of the shorter side.
Solution:
Perimeter of a ||gm ABCD = 22cm
∴ Sum of two consecutive sides = \(\frac { 22 }{ 2 }\)
= 11cm
i.e. AB + BC = 11 cm
AB = 6.5 cm and let BC = x cm
∴ 6.5 + x = 11 cm
x = 11 – 6.5 = 4.5
∴ Shorter side = 4.5 cm
Question 7.
If the angles of a quadrilateral are in the ratio 3 : 5 : 9 : 13. Then find the measure of the smallest angle.
Solution:
Ratio in the angles of a quadrilateral = 3 : 5 : 9 : 13
Let first angle = 3x
Second angle = 5x
Third angle = 9x
and fourth angle = 13x
∵ The sum of angles of a quadrilateral = 360°
∴ 3x + 5x + 9x + 13x = 360°
⇒ 30x = 360° ⇒ x = \(\frac { { 360 }^{ \circ } }{ 30 }\) = 12
∴ Smallest angle = 3x = 3 x 12° = 36°
Question 8.
In parallelogram ABCD if ∠A = (3x – 20°), ∠B = (y + 15)°, ∠C = (x + 40°), then find the value of x and y.
Solution:
In a ||gm ABCD,
∠A = (3x – 20°), ∠B = y + 15°,
∠C = x + 40°
Now, ∠A = ∠C (Opposite angles of a ||gm)
⇒ 3x – 20 = x + 40°
⇒ 3x – x = 40° + 20° ⇒ 2x = 60°
⇒ x = \(\frac { { 60 }^{ \circ } }{ 2 }\) = 30°
and ∠A + ∠B = 180° (Sum of the consecutive angles)
⇒ 3x-20° + y + 15° = 180°
⇒ 3x + y – 5° = 180°
⇒ 3 x 30° +y- 5° = 180°
⇒ 90° – 5° + y = 180
y = 180° – 90° + 5 = 95°
∴ x = 30°, y = 95°
Question 9.
If measures opposite angles of a parallelogram are (60 – x)° and (3x – 4)°, then find the measures of angles of the parallelogram.
Solution:
Opposite angles of a ||gm ABCD are (60 – x)° and (3x – 4°)
But opposite angles of a ||gm are equal, the
60° – x° = 3x – 4° ⇒ 60° + 4° = 3x + x
⇒ 4x = 64° ⇒ x = \(\frac { { 64 }^{ \circ } }{{ 4 }^{ \circ } }\) = 16°
∴ ∠A = 60° – x = 60° – 16° = 44°
But ∠A + ∠B = 180° (sum of consecutive angle)
⇒ 44° + ∠B = 180°
⇒ ∠B = 180° – 44°
⇒ ∠B = 136°
But ∠A = ∠C and ∠B = ∠D (Opposite angles)
∴ Angles are 44°, 136°, 44°, 136°
Question 10.
In a parallelogram ABCD, the bisectors of ∠A also bisect BC at x, find AB : AD.
Solution:
In ||gm ABCD,
Bisectors of ∠A meets BC at X and BX = XC
Draw XY ||gm AB meeting AD at Y
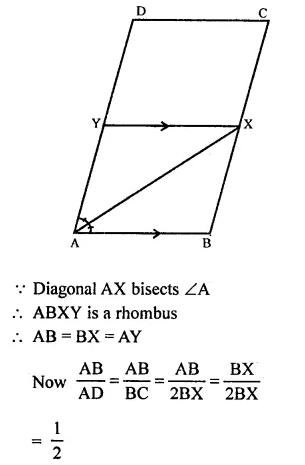
![]()
Question 11.
In the figure, PQRS in an isosceles trapezium find x and y.
Solution:
∵ PQRS is an isosceles trapezium in which
SP = RQ and SR || PQ
∴ ∠P + ∠S = 180° (Sum of co-interior angles)
3x + 2x = 180° ⇒ 5x = 180°
⇒ x = \(\frac { { 180 }^{ \circ } }{ 5 }\) = 36°
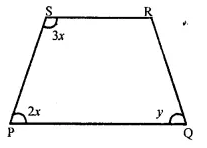
But ∠P = ∠Qm (Base angles of isosceles trapezium)
y = 2x = 2 x 36° = 12°
∴ y = 12°
Hence x = 36°, y = 12°
Question 12.
In the figure ABCD is a trapezium. Find the values of x and y.
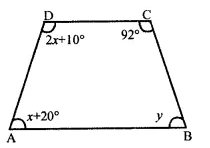
Solution:
In trapezium ABCD,
AB || CD
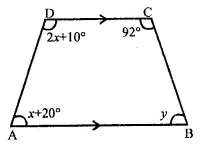
∴ ∠A + ∠D = 180° (Sum of cointerior angles)
x + 20° + 2x + 10° = 180°
3x + 30° = 180°
⇒ 3x= 180° – 30°
3x = 150°
x = \(\frac { { 150 }^{ \circ } }{ 3 }\) = 50°
Similarly, ∠B + ∠C = 180°
⇒ y + 92° = 180°
⇒ y = 180° – 92° = 88°
∴ x = 50°, y = 88°
Question 13.
In the figure, ABCD and AEFG are two parallelograms. If ∠C = 58°, find ∠F.
Solution:
In the figure, ABCD and AEFG are two parallelograms ∠C = 58°
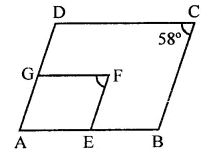
∵ DC || GF and CB || FE (Sides of ||gms)
∴ ∠C = ∠F
But ∠C = 58°
∴ ∠F = 58°
Question 14.
Complete each of the following statements by means of one of those given in brackets against each:
(i) If one pair of opposite sides are equal and parallel, then the figure is ……… (parallelogram, rectangle, trapezium)
(ii) If in a quadrilateral only one pair of opposite sides are parallel, the quadrilateral is …….. (square, rectangle, trapezium)
(iii) A line drawn from the mid-point of one side of a triangle ………. another side intersects the third side at its mid-point, (perpendicular to, parallel to, to meet)
(iv) If one angle of a parallelogram is a right angle, then it is necessarily a …….. (rectangle, square, rhombus)
(v) Consecutive angle of a parallelogram are ……… (supplementary, complementary)
(vi) If both pairs of opposite sides of a quadrilateral are equal, then it is necessarily a ……… (rectangle, parallelogram, rhombus)
(vii) If opposite angles of a quadrilateral are equal, then it is necessarily a ………. (parallelogram, rhombus, rectangle)
(viii)If consecutive sides of a parallelogram are equal, then it is necessarily a …….. (kite, rhombus, square)
Solution:
(i) If one pair of opposite sides are equal and parallel, then the figure is parallelogram.
(ii) If in a quadrilateral only one pair of opposite sides are parallel, the quadrilateral is trapezium.
(iii) A line drawn from the mid-point of one side of a triangle parallel to another side intersects the third side at its mid-point,
(iv) If one angle of a parallelogram is a right angle, then it is necessarily a rectangle.
(v) Consecutive angle of a parallelogram are supplementary.
(vi) If both pairs of opposite sides of a quadrilateral are equal, then it is necessarily a parallelogram.
(vii) If opposite angles of a quadrilateral are equal, then it is necessarily a parallelogram.
(viii) If consecutive sides of a parallelogram are equal, then it is necessarily a rhombus.
Question 15.
In a quadrilateral ABCD, bisectors of A and B intersect at O such that ∠AOB = 75°, then write the value of ∠C + ∠D.
Solution:
In quadrilateral ABCD,
Bisectors of ∠A and ∠B meet at O and ∠AOB = 75°
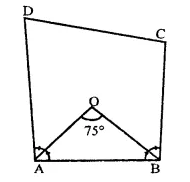
In AOB, ∠AOB = 75°
∴ ∠OAB + ∠OBA = 180° – 75° = 105°
But OA and OB are the bisectors of ∠A and ∠B.
∴ ∠A + ∠B = 2 x 105° = 210°
But ∠A + ∠B + ∠C + ∠D = 360° (Sum of angles of a quad.)
∴ 210° + ∠C + ∠D = 360°
⇒ ∠C + ∠D = 360° – 210° = 150°
Hence ∠C + ∠D = 150°
Question 16.
The diagonals of a rectangle ABCD meet at O. If ∠BOC = 44° find ∠OAD.
Solution:
In rectangle ABCD,
Diagonals AC and BD intersect each other at O and ∠BOC = 44°
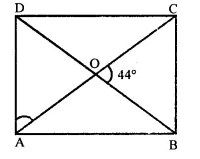
But ∠AOD = ∠BOC (Vertically opposite angles)
∴ ∠AOD = 44°
In ∆AOD,
∠AOD + ∠OAD + ∠ODA = 180° (Sum of angles of a triangle)
⇒ 44° + ∠OAD + ∠OAD = 180° [∵ OA = OD, ∠OAD = ∠ODA]
⇒ 2∠OAD = 180° – 44° = 136°
∴ ∠OAD = \(\frac { { 136 }^{ \circ } }{ 2 }\) = 68°
Question 17.
If ABCD is a rectangle with ∠BAC = 32°, find the measure if ∠DBC.
Solution:
In rectangle ABCD,
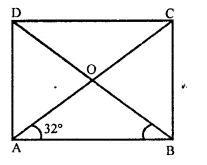
Diagonals bisect each other at O
∠BAC = 32°
∵ OA = OB
∴ ∠OBA Or ∠DBA = ∠BAC = 32°
But ∠ABC = 90° (Angle of a rectangles)
∴ ∠DBC = ∠ABC – ∠DBA
= 90° – 32° = 58°
Question 18.
If the bisectors of two adjacent angles A and B of a quadrilateral ABCD intersect at a point O. Such that ∠C + ∠D = k(∠AOB), then find the value of k.
Solution:
In quadrilateral ABCD,
Bisectors of ∠A and ∠B meet at O
Such that ∠C + ∠D = k (∠AOB)
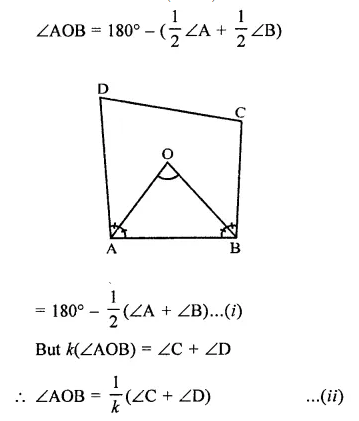
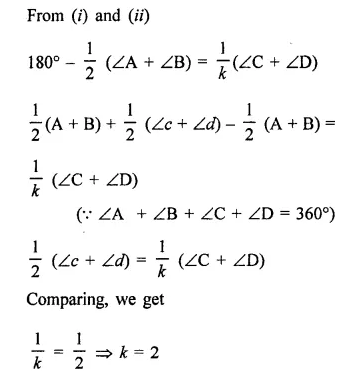
Question 19.
In the figure, PQRS is a rhombus in which the diagonal PR is produced to T. If ∠SRT = 152°, find x, y and z.
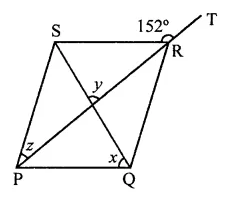
Solution:
In rhombus PQRS,
Diagonal PR and SQ bisect each other at right angles and PR is produced to T such that ∠SRT = 152°
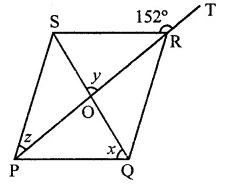
But ∠SRT + ∠SRP = 180° (Linear pair)
⇒ 152° +∠SRP = 180°
⇒ ∠SRP =180°- 152° = 28°
But ∠SPR = ∠SRP (∵ PR bisects ∠P and ∠R)
⇒ z = 28°
y = 90° (∵ Diagonals bisect each other at right angles)
∠RPQ = z = 28°
∴ In ∆POQ,
z + x = 90° ⇒ 28° + x = 90°
⇒ x = 90° – 28° = 62°
∴ x = 62°, y = 90°, z = 28°
Question 20.
In the figure, ABCD is a rectangle in which diagonal AC is produced to E. If ∠ECD = 146°, find ∠AOB.
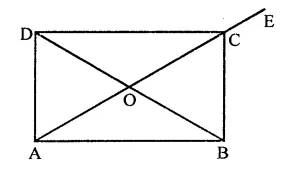
Solution:
In rectangle ABCD,
Diagonals AC and BD bisect each other at O
AC is produced to E and ∠DCE = 146°
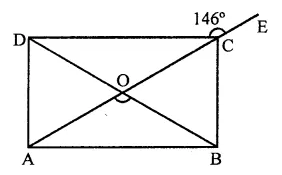
∠DCE + ∠DCA = 180° (Linear pair)
⇒ 146°+ ∠DCA= 180°
⇒ ∠DCA = 180°- 146°
⇒ ∠DCA = 34°
∴ ∠CAB = ∠DCA (Alternate angles)
= 34°
Now in ∆AOB,
∠AOB = 180° – (∠DAB + ∠OBA)
= 180° – (34° + 34°)
= 1803 – 68° = 112°
Hope given RD Sharma Class 9 Solutions Chapter 13 Linear Equations in Two Variables VSAQS are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.