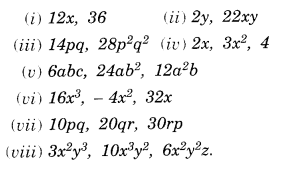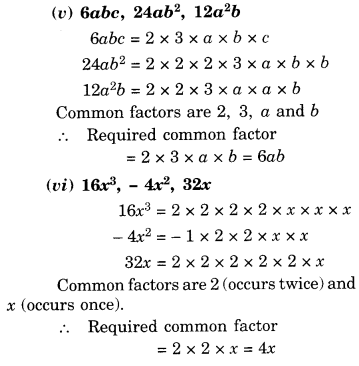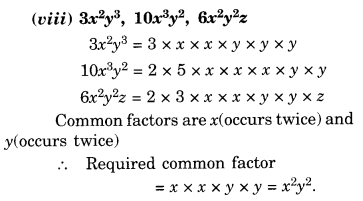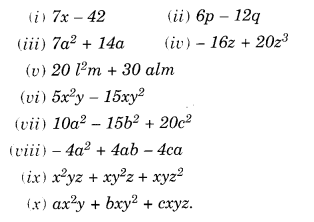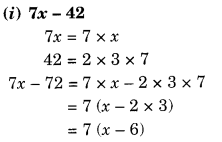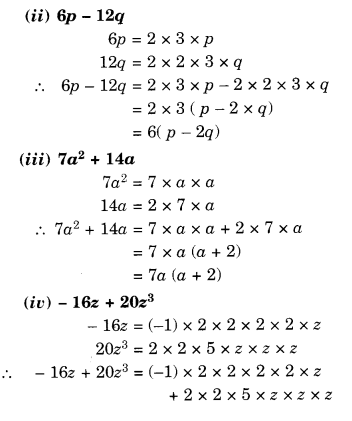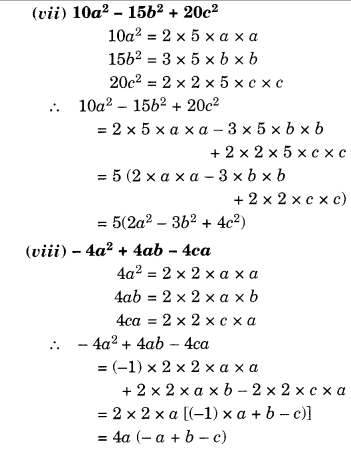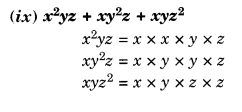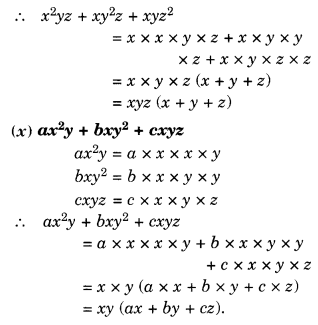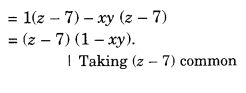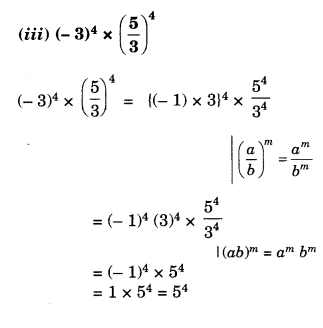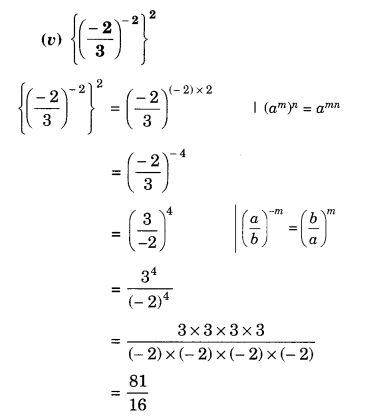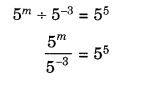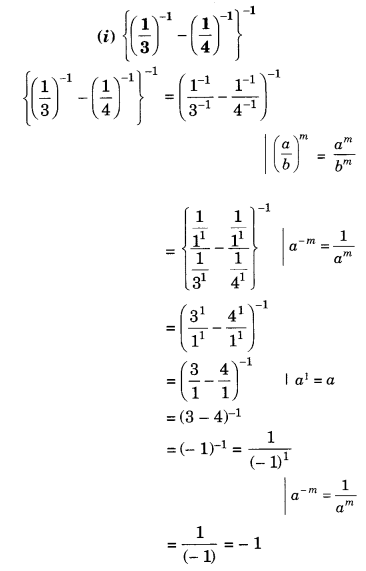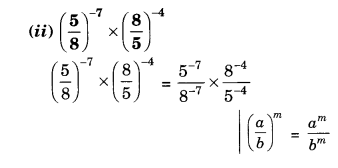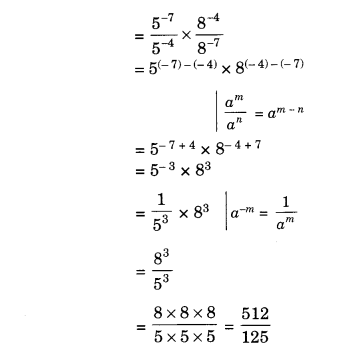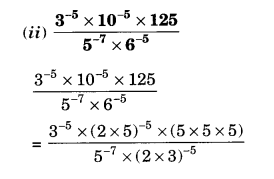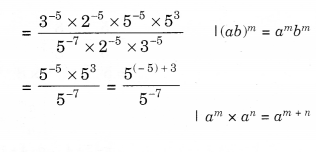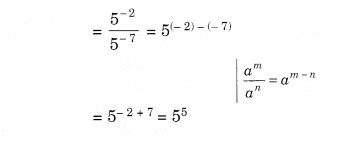NCERT Solutions for Class 8 Maths

NCERT Solutions for Class 8 Maths Chapter 15 Introduction to Graphs Ex 15.1 are part of NCERT Solutions for Class 8 Maths. Here we have given NCERT Solutions for Class 8 Maths Chapter 15 Introduction to Graphs Ex 15.1.

• Introduction to Graphs Class 8 Ex 15.2
• Introduction to Graphs Class 8 Ex 15.3

NCERT Solutions for Class 8 Maths Chapter 15 Introduction to Graphs Ex 15.1

Question 1.
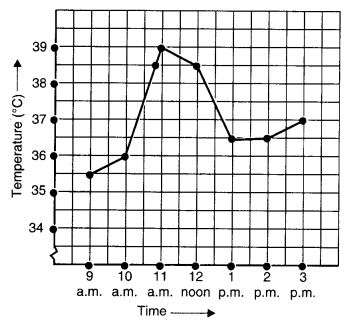
The following graph shows the temperature of a patient in a hospital, recorded every hour.
(a) What was the patient’s temperature at 1 p.m.?
(b) When was the patient’s temperature 38.5°C?
(c) The patient’s temperature was the same two times during the period given. What were these two times?
(d) What was the temperature at 1.30 p.m.? How did you arrive at your answer?
(e) During which periods did the patient’s temperature showed an upward trend?

Solution.
(а) The patient’s temperature at 1 p.m. was 36.5°C.
(b) The patient’s temperature was 38.5°C at 10.50 a.m. and 12 noon.
(c) The two times when the patient’s temperature was the same were 1 p.m. and 2 p.m.
(d) The temperature at 1.30 p.m. was 36.5°C.
From the graph, we see that the temperature was constant from 1 p.m. to 2 p.m. Since 1.30 p.m. comes in between 1 p.m. and 2 p.m., therefore we arrived at our answer.
(e) The patient’s temperature showed an upward trend during the periods 9 a.m. to 10 a.m., 10 a.m. to 11 a.m. and 2 p.m. to 3 p.m.

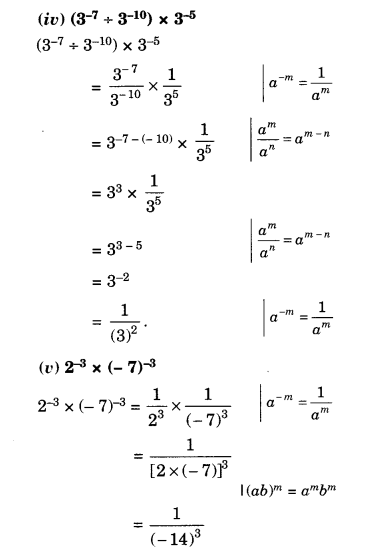
Question 2.
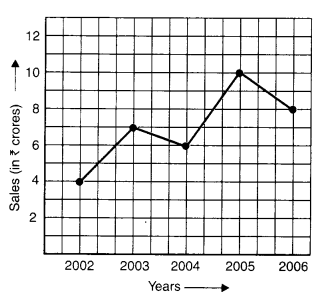
The following line graph shows the yearly sales figures for a manufacturing company.
(a) What were the sales in
(i) 2002
(ii) 2006?

(b) What were the sales in
(i) 2003
(ii) 2005?

(c) Compute the difference between sales in 2002 and 2006.
(d) In which year was there the greatest difference between the sales as compared to its previous year?

Solution.
(а) The sales in
(i) 2002 were ₹ 4 crores and in
(ii) 2006 were ₹ 8 crores.

(b) The sales in
(i) 2003 were ₹ 7 crores and in
(ii) 2005 were ₹ 10 crores.

(c) The difference between the sales in 2002 and 2006
= ₹ 8 crores – ₹ 4 crores = ₹ 4 crores

(d) The difference between sales in 2002 and 2003
= ₹ 7 crores – ₹ 4 crores = ₹ 3 crores
The difference between sales in 2003 and 2004
= ₹ 7 crores – ₹ 6 crores = ₹ 1 crore
The difference between the sales in 2004 and 2005
= ₹ 10 crores – ₹ 6 crores = ₹ 4 crores
The difference between sales in 2005 and 2006
= ₹ 10 crores – ₹ 8 crores = ₹ 2 crores
Therefore, in year 2005 the difference between the sales as compared to its previous year was the greatest.

Question 3.
For an experiment in Botany, two different plants, plant A and plant B were grown under similar laboratory conditions. Their heights were measured at the end of each week for 3 weeks. The results are shown by the following graph.

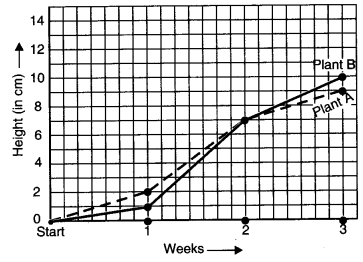
(a) How high was Plant A after
(i) 2 weeks
(ii) 3 weeks?

(b) How high was Plant B after
(i) 2 weeks
(ii) 3 weeks?

(c) How much did Plant A grow during
(d) How much did Plant B grow from the end of the 2nd week to the end of the 3rd week?
(e) During which week did Plant A grow most?
(f) During which week did Plant B grow least?
(g) Were the two plants of the same height during any week shown here? Specify.
Solution.
(а) The Plant A
after (i) 2 weeks was 7 cm high and
after (ii) 3 weeks was 9 cm high.

(b) The Plant B
after (i) 2 weeks was 7 cm high and
after (ii) 3 weeks was 10 cm high.

(c) The Plant A grew 9 cm – 7 cm = 2 cm during the 3rd week.

(d) From the end of the 2nd week to the end of the 3rd week, Plant B grew
= 10 cm – 7 cm = 3 cm.

(e) The Plant A grew in 1st week
= 2 cm – 0 cm = 2 cm
The Plant A grew in 2nd week
= 7 cm – 2 cm = 5 cm
The Plant A grew in 3rd week
= 9 cm – 7 cm = 2 cm
Therefore, Plant A grew mostly in the second week.

(f) Plant B grew in 1st week
= 1 cm – 0 cm = 1 cm
Plant B grew in 2nd week
= 7 cm – 1 cm = 6 cm
Plant B grew in 3rd week
= 10 cm – 7 cm = 3 cm
Therefore, Plant B grew least in the first week.

(g) At the end of 2nd week, the two plants shown here were of the same height.

Question 4.
The following graph shows the temperature forecast and the actual temperature for each day of a week:

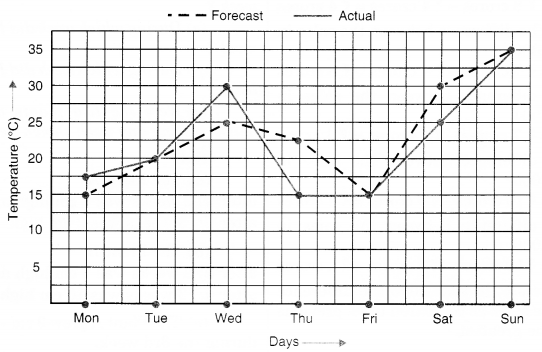
(a) On which days was the forecast temperature the same as the actual temperature?
(b) What was the maximum forecast temperature during the week?
(c) What was the minimum actual temperature during the week?
(d) On which day did the actual temperature differ the most from the forecast temperature?
Solution.
(a) The forecast temperature was the same as the actual temperature on Tuesday, Friday and Sunday.
(b) The maximum forecast temperature during the week was 35°C.
(c) The minimum actual temperature during the week was 15°C.
(d)

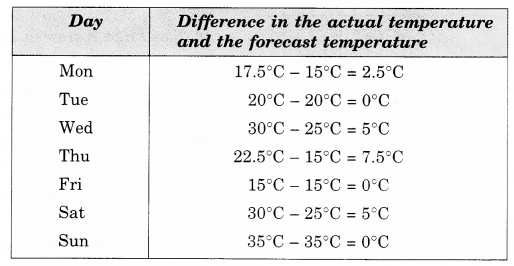
Therefore, the actual temperature differed the most from the forecast temperature on Thursday.

Question 5.
Use the tables below to draw linear graphs.
(a) The number of days a hill side city received snow in different years.

(b) Population (in thousands) of men and women in a village in different years.

Solution.
(a)

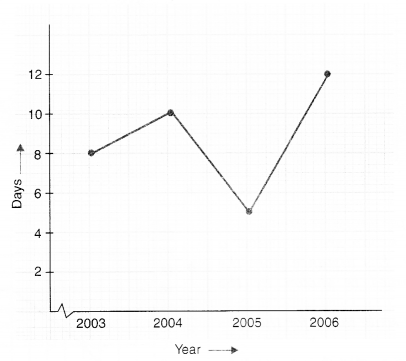
(b)

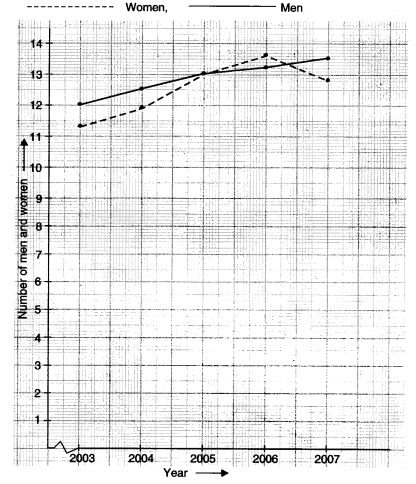
Question 6.
Courier-person cycles from a town to a neighboring suburban area to deliver a parcel to a merchant. His distance from the town at different times is shown by the following graph.
(a) What is the scale taken for the time axis?
(b) How much time did the person take for the travel?
(c) How far is the place of the merchant from the town?
(d) Did the person stop on his way? Explain.
(e) During which period did he ride fastest?

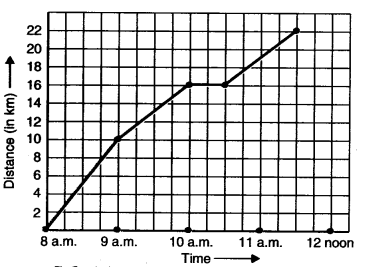
Solution.
(a) The scale taken for the time axis is 4 units = 1 hour.
(b) The time taken by the person for the travel 8 a.m. to 11.30 a.m. = \(3\frac { 1 }{ 2 } \) hours.
(c) The place of the merchant from the town in 22 km.
(d) Yes. This is indicated by the hori¬zontal part of the graph (10 a.m. – 10.30 a.m.)
(e) He rides fastest between 8 a.m. and 9 a.m. (As line is more steep in this period).

Question 7.
Can there be a time-temperature graph as follows ? Justify your answer.


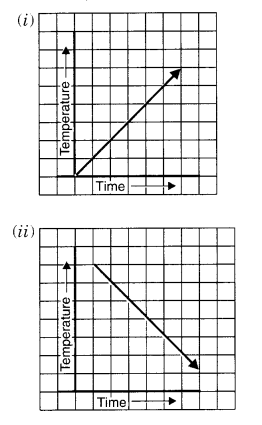
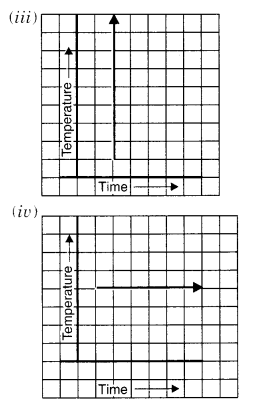
Solution.
(i) Yes; it can be
It shows a time-temperature graph. It shows an increase in temperature with an increase in time.
(ii) Yes; it can be
It shows a time-temperature graph.
It shows a decrease in temperature with increase in time.
(iii) It cannot be a time-temperature graph because it shows infinitely many different temperatures at one particular time which is not possible.
(iv) Yes; it can be
It shows a time-temperature graph,
It shows a fixed temperature at different times.

We hope the NCERT Solutions for Class 8 Maths Chapter 15 Introduction to Graphs Ex 15.1 help you. If you have any query regarding NCERT Solutions for Class 8 Maths Chapter 15 Introduction to Graphs Ex 15.1, drop a comment below and we will get back to you at the earliest.

NCERT Solutions for Class 8 Maths Chapter 14 Factorisation Ex 14.1 are part of NCERT Solutions for Class 8 Maths. Here we have given NCERT Solutions for Class 8 Maths Chapter 14 Factorisation Ex 14.1.

• Factorisation Class 8 Ex 14.2
• Factorisation Class 8 Ex 14.3
• Factorisation Class 8 Ex 14.4

NCERT Solutions for Class 8 Maths Chapter 14 Factorisation Ex 14.1

Question 1.
Find the common factors of the given terms:

Solution.

Question 2.
Factorise the following expressions:

Solution.

Question 3.
Factorise:

Solution.

We hope the NCERT Solutions for Class 8 Maths Chapter 14 Factorisation Ex 14.1 help you. If you have any query regarding NCERT Solutions for Class 8 Maths Chapter 14 Factorisation Ex 14.1, drop a comment below and we will get back to you at the earliest.

NCERT Solutions for Class 8 Maths Chapter 13 Direct and Indirect Proportions Ex 13.1 are part of NCERT Solutions for Class 8 Maths. Here we have given NCERT Solutions for Class 8 Maths Chapter 13 Direct and Indirect Proportions Ex 13.1.

• Direct and Indirect Proportions Class 8 Ex 13.2

NCERT Solutions for Class 8 Maths Chapter 13 Direct and Indirect Proportions Ex 13.1

Question 1.
Following are the car parking charges near a railway station up to
4 hours ₹ 60
8 hours ₹ 100
12 hours ₹ 140
24 hours ₹ 180
Check if the parking charges are in direct proportion to the parking time.
Solution.
We have
\(\frac { 60 }{ 4 } =\frac { 15 }{ 1 } \)
\(\frac { 100 }{ 8 } =\frac { 25 }{ 2 } \)
\(\frac { 140 }{ 12 } =\frac { 35 }{ 3 } \)
\(\frac { 180 }{ 24 } =\frac { 15 }{ 2 } \)
Since all the values are not the same, therefore, the parking charges are not in direct proportion to the parking time.

Question 2.
A mixture of paint is prepared by mixing 1 part of red pigments with 8 parts of the base. In the following table, find the parts othe f base that need to be added.

Solution.
Sol. Let the number of parts of red pigment is x and the number of parts of the base is y.
As the number of parts of red pigment increases, a number of parts of the base also increases in the same ratio. So it is a case of direct proportion.
We make use of the relation of the type

Question 3.
In Question 2 above, if 1 part of a red pigment requires 75 mL of the base, how much red pigment should we mix with 1800 mL of base?
Solution.
Let the number of parts of red pigment is x and the amount of base be y mL.
As the number of parts of red pigment increases, the amount of base also increases in the same ratio. So it is a case of direct proportion. We make use of the relation of the type.

Question 4.
A machine in a soft drink factory fills 840 bottles in six hours. How many bottles will it fill in five hours?
Solution.
Let the machine fill x bottles in five hours. We put the given information in the form of a table as shown below :
Number of bottles filled 840 x2
Number of hours 6 5
More the number of hours, more the number of bottles would be filled. So, the number of bottles filled and the number of hours are directly proportional to each other.
So, \(\frac { { x }_{ 1 } }{ { x }_{ 2 } } =\frac { { y }_{ 1 } }{ { y }_{ 2 } } \)
⇒ \(\frac { 840 }{ { x }_{ 2 } } =\frac { 6 }{ 5 } \)
⇒ \(6{ x }_{ 2 }=840\times 5\)
⇒ \({ x }_{ 2 }=\frac { 840\times 5 }{ 6 } \)
⇒ \({ x }_{ 2 }=700\)
Hence, 700 bottles will be filled.

Question 5.
A photograph of a bacteria enlarged 50,000 times attains a length of 5 cm as shown in the diagram. What is the actual length of the bacteria ? If the photograph is enlarged 20,000 times only, what would be its enlarged length?

Solution.
Actual length of the bacteria
= \(\frac { 5 }{ 50000 } \)cm
= \(\frac { 1 }{ 10000 } \) = \({ 10 }^{ -4 }\)cm
10000
Let the enlarged length be y2 cm. We put the given information in the form of a table as shown below:
Number of times Length attained
photograph enlarged (in cm)
50.000 5
20.000 y₂
More the number of times a photograph of a bacteria is enlarged, more the length attained. So, the number of times a photograph of a bacteria is enlarged and the length attained are directly proportional to each other.
So,\(\frac { { x }_{ 2 } }{ { y }_{ 2 } } =\frac { { x }_{ 2 } }{ { y }_{ 2 } } \)
⇒ \(\frac { 50000 }{ 5 } =\frac { 20000 }{ { y }_{ 2 } } \)
⇒ \(50000{ y }_{ 2 }=5\times 20000\)
⇒ \({ y }_{ 2 }=\frac { 5\times 20000 }{ 50000 } \)
⇒ \({ y }_{ 2 }=2\)
Hence, its enlarged length would be
2 cm.

Question 6.
In a model of a ship, the mast is 9 cm high, while the mast of the actual ship is 12 m high. If the length of the ship is 28 m, how long is the model ship ?

Solution.

Question 7.
Suppose 2 kg of sugar contains 9 x 106 crystals. How many sugar crystals are there in
(i) 5 kg of sugar?
(ii) 1.2 kg of sugar?
Solution.
Suppose the amount of sugar is x kg and the number of crystals is y.
We put the given information in the form of a table as shown below:

As the amount of sugar increases, the number of crystals also increases in the same ratio. So it is a case of direct proportion. We make use of the relation of the type \(\frac { { x }_{ 1 } }{ { y }_{ 1 } } =\frac { { x }_{ 2 } }{ { y }_{ 2 } } \)

Question 8.
Rashmi has a roadmap with a scale of 1 cm representing 18 km. She drives on a T’oad for 72 km. What would be her distance covered in the map?
Solution.
Let the distance covered in the map be x cm. Then,
1 : 18 = x : 72
⇒ \(\frac { 1 }{ 18 } =\frac { x }{ 72 }\)
⇒ \(x=\frac { 72 }{ 18 } \)
⇒ x = 4
Hence, the distance covered in the map would be 4 cm.

Question 9.
A5 m 60 cm high vertical pole casts a shadow 3 m 20 cm long. Find at the same time
(i) the length of the shadow cast by another pole 10 m 50 cm high
(ii) the height of a pole which casts a shadow 5 m long.
Solution.
Let the height of the vertical pole be x m and the length of the shadow be y m.
We put the given information in the form of a table as shown below:

Question 10.
A loaded truck travels 14 km. in 25 minutes. If the speed remains the same, how far can it travel in 5 hours?
Solution.
Two quantities x and y which vary in direct proportion have the relation

We hope the NCERT Solutions for Class 8 Maths Chapter 13 Direct and Indirect Proportions Ex 13.1 help you. If you have any query regarding NCERT Solutions for Class 8 Maths Chapter 13 Direct and Indirect Proportions Ex 13.1, drop a comment below and we will get back to you at the earliest.

NCERT Solutions for Class 8 Maths Chapter 12 Exponents and Powers Ex 12.1 are part of NCERT Solutions for Class 8 Maths. Here we have given NCERT Solutions for Class 8 Maths Chapter 12 Exponents and Powers Ex 12.1.

• Exponents and Powers Class 8 Ex 12.2

NCERT Solutions for Class 8 Maths Chapter 12 Exponents and Powers Ex 12.1

Question 1.
Evaluate :
(i) \({ 3 }^{ -2 }\)
(ii) \({ -4 }^{ -2 }\)
(iii) \(({ \frac { 1 }{ 2 } ) }^{ -5 }\)
Solution.

Question 2.
Simplify and express the result in power notation with positive exponent.

Solution.

Question 3.
Fmd the value of:

Solution.

Question 4.
Evaluate
(i) \(\frac { { 8 }^{ -1 }\times { 5 }^{ 3 } }{ { 2 }^{ -4 } } \)
(ii) \(({ 5 }^{ -1 }\times { 2 }^{ -1 })\times { 6 }^{ -1 }\)
Solution.

Question 5.
Find the value of m for which \({ 5 }^{ m }+{ 5 }^{ -3 }={ 5 }^{ 5 }\)
Solution.

Question 6.
Evaluate :

Solution.

Question 7.
Simplify:
(i) \(\frac { 25\times { t }^{ -4 } }{ { 5 }^{ -3 }\times 10\times { t }^{ -8 } } \) (t ≠ 0)
(ii) \(\frac { { 3 }^{ -5 }\times { 10 }^{ -5 }\times 125 }{ { 5 }^{ -7 }\times { 6 }^{ -5 } } \)
Solution.

We hope the NCERT Solutions for Class 8 Maths Chapter 12 Exponents and Powers Ex 12.1 help you. If you have any query regarding NCERT Solutions for Class 8 Maths Chapter 12 Exponents and Powers Ex 12.1, drop a comment below and we will get back to you at the earliest.

NCERT Solutions for Class 8 Maths Chapter 11 Mensuration Ex 11.1 are part of NCERT Solutions for Class 8 Maths. Here we have given NCERT Solutions for Class 8 Maths Chapter 11 Mensuration Ex 11.1.

• Mensuration Class 8 Ex 11.2
• Mensuration Class 8 Ex 11.3
• Mensuration Class 8 Ex 11.4

NCERT Solutions for Class 8 Maths Chapter 11 Mensuration Ex 11.1

Question 1.
A square and a rectangular field with measurements as given in the figure have the same perimeter. Which field has a larger area?


Solution.
Area of the square field = a x a
= 60 m x 60 m = 3,600 \({ m }^{ 2 }\)
Perimeter of the square field = 4a
= 4 x 60 m = 240 m
∴ Perimeter of rectangular field = 240 m
⇒ 2(l + b) = 240
⇒ 2(80 + b) = 240
where b m is the breadth of the rectangular field
⇒ 80 + b = \(\frac { 240 }{ 2 } \) ⇒ 80 + bx = 120
⇒ b = 120 – 80 = 40
∴ Breadth = 40 m
∴ Area of rectangular field
= l x b = 80 m x 40 m = 3,200 \({ m }^{ 2 }\)
So, the square field (a) has a larger area

Question 2.
Mrs. Kaushik has a square plot ‘ with the measurement as shown in the figure. She wants to construct a house in the middle of the plot. A garden is developed around the house. Find the total cost of developing a: garden around the house at the rate of ₹ 55 per \({ m }^{ 2 }\).
Solution.
Area of the square plot = a x a
= 25 x 25 \({ m }^{ 2 }\) = 625 \({ m }^{ 2 }\)
Area of the house = a x b
= 20 x 15 \({ m }^{ 2 }\) = 300 \({ m }^{ 2 }\)
∴ Area of the garden
= Area of the square plot – Area of the house
= 625 \({ m }^{ 2 }\) – 300 \({ m }^{ 2 }\)
= 325 \({ m }^{ 2 }\)
∵ The cost of developing the garden per square metre = ₹ 55.
∴ Total cost of developing the garden
= ₹ 325 x 55
= ₹ 17,875.

Question 3.
The shape of a garden is rectangular in the middle and semicircular at the ends as shown in the diagram. Find the area and the perimeter of this garden.

Solution.

Question 4.
A flooring tile has the shape of a parallelogram whose base is 24 cm and the cor-responding height is 10 cm. How many such tiles are required to cover a floor of area 1080 m2? (If required you can split the tiles in whatever way you want to fill up the corners).
Solution.
Area of a flooring tile = bh
= 24 x 10 \({ cm }^{ 2 }\)
= 240 \({ cm }^{ 2 }\)
Area of the floor
= 1080 \({ m }^{ 2 }\)
= 1080 x 100 x 100 \({ cm }^{ 2 }\)
∵ m2 = 100 x 100 \({ cm }^{ 2 }\)

∴ Number of tiles required to cover the floor
=\(\frac { Area\quad of\quad the\quad floor\quad }{ Area\quad of\quad a\quad flooring\quad tile } \)
= \(\frac { 1080\times 100\times 100\quad }{ 240 } \)
= 45000.

Question 5.
An ant is moving around a few food pieces of different shapes scattered on the floor. For which food-piece would the ant have to take a longer round? Remember, the circumference of a circle can be obtained by using the expression c = 2πr, where r is the radius of the circle.


Solution.

We hope the NCERT Solutions for Class 8 Maths Chapter 11 Mensuration Ex 11.1 help you. If you have any query regarding NCERT Solutions for Class 8 Maths Chapter 11 Mensuration Ex 11.1, drop a comment below and we will get back to you at the earliest.