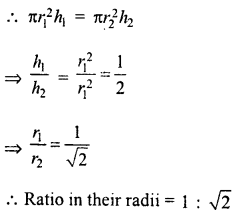Maths RD Sharma Solutions Class 8

RD Sharma Class 8 Solutions Chapter 21 Mensuration II (Volumes and Surface Areas of a Cubiod and a Cube) Ex 21.1

These Solutions are part of RD Sharma Class 8 Solutions. Here we have given RD Sharma Class 8 Solutions Chapter 21 Mensuration II Ex 21.1

Other Exercises

• RD Sharma Class 8 Solutions Chapter 21 Mensuration II Ex 21.1
• RD Sharma Class 8 Solutions Chapter 21 Mensuration II Ex 21.2
• RD Sharma Class 8 Solutions Chapter 21 Mensuration II Ex 21.3
• RD Sharma Class 8 Solutions Chapter 21 Mensuration II Ex 21.4

Question 1.
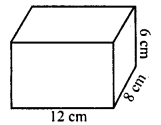
Find the volume of a cuboid whose
(i) length = 12 cm, breadth = 8 cm, height = 6 cm
(ii) length = 1.2 m, breadth = 30 cm, height = 15 cm
(iii) length = 15 cm, breadth = 2.5 dm, height = 8 cm

Solution:
In a cuboid,
(i) Length (l) = 12 cm
Breadth (b) = 8 cm
Height (h) = 6 cm
∴ Volume = Ibh = 12 x 8 x 6 cm³ = 576 cm³
(ii) Length (l) = 1.2 m = 120 cm
breadth (6) = 30 cm
Height (h) = 15 cm
∴ Volume = Ibh = 120 x 30 x 15 cm³ = 54000 cm³
(iii) Length (l) = 15 cm
Breadth (b) = 2.5 dm = 25 cm
Height (h) = 8 cm
∴ Volume = Ibh
= 15 x 25 x 8 cm³ = 3000 cm²

Question 2.
Find the volume of the cube whose side is
(i) 4 cm
(ii) 8 cm
(iii) 1.5 dm
(iv) 1.2 m
(v) 25 mm.
Solution:
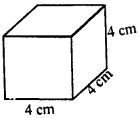
(i) Side of a cube (a) = 4 cm
∴ Volume = a3 = (4)³ cm³ = 4 x 4 x 4 = 64 cm³

(ii) Side of cube (a) = 8 cm
∴ Volume = a3 = (8)³ 4 cm
= 8 x 8 x 8 cm³ = 512 cm³
(iii) Side of cube (a) = 1.5 dm = 15 cm
∴ Volume = a³ = (1.5)3 dm² = (15)³ cm³
= 15 x 15 x 15 = 3375 cm³
(iv) Side of cube (a) = 1.2 m = 120 cm
∴ Volume = a³ = (120)³ cm³
= 120 x 120 x 120 = 1728000 cm³
(v) Side of cube (a) = 25 mm = 2.5 cm.
∴ Volume = a³ = (2.5)³ cm³
= 2.5 x 2.5 x 2.5 cm³ = 15.625 cm³

Question 3.
Find the height of a cuboid of volume 100 cm3 whose length and breadth are 5 cm and 4 cm respectively.
Solution:
Volume of a cuboid =100 cm³
Length (1) = 5 cm
and breadth (b) = 4 cm

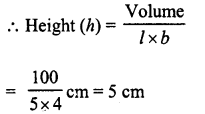
Question 4.
A cuboidal vessel is 10 cm long and 5 cm wide, how high it must be made to hold 300 cm3 of a liquid ?
Solution:
Volume of the liquid in the vessel = 300 cm³
Length (l)= 10 cm
Breadth (b) = 5 cm

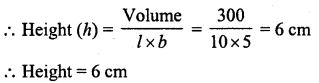
Question 5.
A milk container is 8 cm long and 50 cm wide. What should be its height so that it can hold 4 litres of milk ?
Solution:
Capacity of milk = 4 litres
∴ Volume of the container = 4 x 1000 cm³ = 4000 cm³
Length (l) = 8 cm
Width (b) = 50 cm

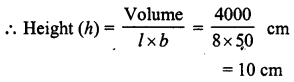
Question 6.
A cuboidal wooden block contains 36 cm³ wood. If it be 4 cm long and 3 cm wide, find its height.
Solution:
Volume of wooden cuboid block = 36 cm³
Length (l) = 4 cm
Breadth (b) = 3 cm

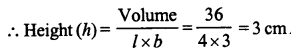
Question 7.
What will happen to the volume of a cube, if its edge is (i) halved (ii) trebled ?
Solution:
Let side of original cube = a cm
∴ Volume = a³ cm³
(i) In first case,

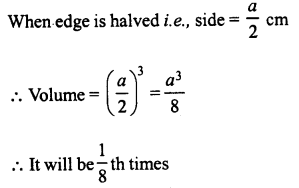
(ii) In second case, when side (edge) is trebled, then side = 3a
∴ Volume = (3a)³ = 27a³
∴ It will be 27 times

Question 8.
What will happen to the volume of a cuboid if its (i) Length is doubled, height is same and breadth is halved ? (ii) Length is doubled, height is doubled and breadth is same ?
Solution:
Let l, b and h be the length, breadth and height of the given cuboid respectively.
∴ Volume = lbh.
(i) Length is doubled = 21

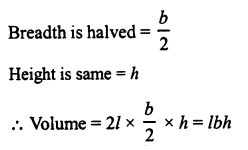
∴ The volume will be the same.
(ii) Length is doubled = 21
breadth is same = b height is doubled = 2h
∴ Volume = 2l x b x 2h = 4 lbh
∴ Volume will be 4 times

Question 9.
Three cuboids of dimensions 5 cm x 6 cm x 7 cm, 4 cm x 7 cm * 8 cm and 2 cm x 3 cm x 13 cm are melted and a cube is made. Find the side of cube.
Solution:
Dimensions of first cuboid = 5 cm x 6 cm x 7 cm
∴ Volume = 5 x 6 x 7 = 210 cm³
Dimensions of second cuboid = 4 cm x 7 cm x 8 cm
∴ Volume = 4x 7 x 8 = 224 cm³
Dimensions of third cuboid = 2 cm x 3 cm x 13 cm
∴ Volume = 2 x 3 x 13 = 78 cm³
Total volume of three cubes = 210 + 224 + 78 cm3 = 512 cm³
∴ Volume of cube = 512 cm³

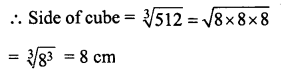
Question 10.
Find the weight of solid rectangular iron piece of size 50 cm x 40 cm x 10 cm, if 1 cm3 of iron weighs 8 gm.
Solution:
Dimension of cuboidal iron piece = 50 cm x 40 cm x 10 cm
∴ Volume = 50 x 40 x 10 = 20000 cm³
Weight of 1 cm³ = 8 gm
∴ Total weight of piece = 20000 x 8 gm

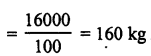
Question 11.
How many wooden cubical blocks of side 25 cm can be cut from a log of wood of size 3 m by 75 cm by 50 cm, assuming that there is no wastage ?
Solution:
Length of log (l) = 3 m = 300 cm.
Breadth (b) = 75 cm
and height (h) = 50 cm
∴ Volume of log = lbh = 300 x 75 x 50 cm3 = 1125000 cm³
Side of cubical block = 25 cm
∴ Volume of one block = a² = 25 x 25 x 25 cm3 = 15625 cm³
∴ Number of blocks to be cut out

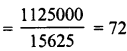
Question 12.
A cuboidal block of silver is 9 cm long, 4 cm broad and 3.5 cm in height. From it, beads of volume 1.5 cm² each are to be made. Find the number of beads that can be made from the block ?
Solution:
Length of block (l) = 9 cm
Breadth (b) = 4 cm
and height (h) = 3.5 cm
∴ Volume = l x b x h = 9 x 4 x 3.5 cm³ = 126 cm³
Volume of one bead = 1.5 cm³
∴ Number of beads = \(\frac { 126 }{ 105 }\) = 84

Question 13.
Find the number of cuboidal boxes measuring 2 cm by 3 cm by 10 cm which can be stored in a carton whose dimensions are 40 cm, 36 cm and 24 cm.
Solution:
Length of cuboidal box (l) = 2 cm
breadth (b) = 3 cm
and height (h) = 10 cm
∴ Volume = lx b x h = 2 x 3 x 10 = 60 cm³
Volume of carton = 40 x 36 x 24 cm³
= 34560 cm³
∴ Number of boxes to be height in the carton

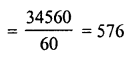
Question 14.
A cuboidal block of solid iron has dimensions 50 cm, 45 cm and 34 cm. How many cuboids of size 5 cm by 3 cm by 2 cm can be obtained from the block ? Assume cutting causes no wastage.
Solution:
Dimensions of block = 50 cm, 45 cm, 34 cm
∴ Volume = 50 x 45 x 34 = 76500 cm³
Size of cuboid = 5 cm x 3 cm x 2 cm
∴ Volume of cuboid =  5 x 3 x 2 = 30 cm³

Question 15.
A cube A has side thrice as long as that of cube B ? What is the ratio of the volume of cube A to that of cube B ?
Solution:
Let side of cube B = a
Then Volume = a³
and side of cube A = 3a
Volume = (3a)³ = 3a x 3a x 2a = 27a³
∴ Ratio of volume’s A and B = 27a³ : a³
= 27 : 1

Question 16.
An ice-cream brick measures 20 cm by 10 cm by 7 cm. How many such bricks can be stored in a deep fridge whose inner dimensions are 100 cm by 50 cm by 42 cm ?
Solution:
Dimensions of ice cream brick = 20 cm x 10 cm x 7 cm
∴ Volume = 20 x 10 x 7 cm³ = 1400 cm³
Dimensions of inner of fridge = 100 cm x 50 cm x 42 cm = 210000 cm³
∴ Number of bricks to be kept in the fridge

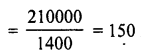
Question 17.
Suppose that there are two cubes, having edges 2 cm and 4 cm, respectively. Find the volume V₁ and V₂ of the cubes and compare them.
Solution:
Side of first cube (a) = 2 cm
∴ Volume (V₁) = a³ = (2) = 8 cm³
Similarly side of second cube = 4 cm
and volume (V₂) = (4)³ = 64 cm³
Now V₂ = 64 cm³ = 8 x 8 cm³
= 8 x V₁
⇒ V₂ = 8V₁

Question 18.
A tea-packet measures 10 cm x 6 cm x 4 cm.How many such tea-packets can be placed in a cardboard box of dimensions 50 cm x 30 cm x 0.2 m ?
Solution:
Dimensions of tea-packet = 10cm x 6cm x 4 cm
∴ Volume =10 x 6 x 4 = 240 cm³
Dimensions of box = 50 cm x 30 cm x 0.2 m
= 50 cm x30 cm x20 cm
∴ Volume = 50 x 30 x 20 = 30000 cm³
∴ Number of tea-packets to be kept = \(\frac { 30000 }{ 240 }\)

Question 19.
The weight of a metal block of size 5 cm by 4 cm by 3 cm is 1 kg. Find the weight of a block of the same metal of size 15 cm by 8 cm by 3 cm.
Solution:
Dimensions of a metal block = 5 cm x 4 cm x 3 cm = 5 x 4 x 3 = 60 cm³
Dimensions of a second block = 15 cm x 8 cm x 3 cm = 15 x 8 x 3 = 360 cm³
But weight of first block = 1 kg
∴ Weight of second block
= \(\frac { 1 }{ 16 }\) x 360 = 6 kg

Question 20.
How many soap cakes can be placed in a box of size 56 cm x 0.4 m x 0.25 m, it the size of soap cake is 7 cm x 5 cm x 2.5 cm ?
Solution:
Size of box = 56 cm x 0.4 m x 0.25 m = 56 cm x 40 cm x 25 cm
∴ Volume = 56 x 40 x 25 cm³ = 56000 cm³
Size of a soap cake = 7 cm x 5 cm x 2.5 cm
∴ Volume = 7 x 5 x 2.5 cm³ = 87.5 cm³
∴ Number of cakes to be kept in the box
= \(\frac { 56000 }{ 87.5 }\) = 640

Question 21.
The volume of a cuboid box is 48 cm3. If its height and length are 3 cm and 4 cm respectively, find its breadth.
Solution:
Volume of cuboid box = 48 cm³
Length (l) = 4 cm
Height = (h) = 3 cm

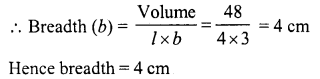
Hope given RD Sharma Class 8 Solutions Chapter 21 Mensuration II Ex 21.1 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 8 Solutions Chapter 22 Mensuration III (Surface Area and Volume of a Right Circular Cylinder) Ex 22.2

These Solutions are part of RD Sharma Class 8 Solutions. Here we have given RD Sharma Class 8 Solutions Chapter 22 Mensuration III Ex 22.2

Other Exercises

• RD Sharma Class 8 Solutions Chapter 22 Mensuration III Ex 22.1
• RD Sharma Class 8 Solutions Chapter 22 Mensuration III Ex 22.2

Question 1.
Find the volume of a cuboid whose
(i) r = 3.5 cm, h = 40 cm
(ii) r = 2.8 m, h = 15 m
Solution:
(i) Radius (r) = 3.5 cm
Height (h) = 40 cm
Volume of cylinder = πr²h

Question 2.
Find the volume of a cylinder, if the diameter (d) of its base and its altitude (h) are:
(i) d= 21 cm, h = 10 cm
(ii) d = 7 m, h = 24 m.
Solution:
(i) Diameter (d) = 21 cm

Question 3.
The area of the base of a right circular cylinder is 616 cm3 and its height is 25 cm. Find the volume of the cylinder.
Solution:
Base area of cylinder = 616 cm²
Height (h) = 25 cm.
∴ Volume = Area of base x height
= 616 x 25 cm³ = 15400 cm³

Question 4.
The circumference of the base of a cylinder is 88 cm and its height is 15 cm. Find the volume of the cylinder.
Solution:
Circumference of the base of cylinder = 88 cm
Let r be the radius

Question 5.
A hollow cylindrical pipe is 21 dm long. Its outer and inner diameters are 10 cm and 6 cm respectively. Find the volume of the copper used in making the pipe.
Solution:
Length (Height) of hollow cylindrical pipe = 21 dm = 210 cm
Inner diameter = 6 cm
Outer diameter = 10 cm

Question 6.
Find the (i) curved surface area (ii) total surface area and (iii) volume of a right circular cylinder whose height is 15 cm and the radius of the base is 7 cm
Solution:
Radius of the cylider (r) = 7 cm
and height (h) = 15 cm
(i) Curved surface area = 2πrh

Question 7.
The diameter of the base of a right circular cylinder is 42 cm and its height is 10 cm. Find the volume of the cylinder.
Solution:
Diameter of the base of cylinder = 42 cm

Question 8.
Find the volume of a cylinder, the diameter of whose base is 7 cm and height being 60 cm. Also, find the capacity of the cylinder in litres.
Solution:
Diameter of cylinder = 7 cm

Question 9.
A rectangular strip 25 cm x 7 cm is rotated about the longer side. Find the volume of the solid, thus generated.
Solution:
Size of rectangular strip = 25 cm x 7 cm
By rotating, about the longer side, we find a right circular cylinder,
then the radius of cylinder (r) = 7 cm

Question 10.
A rectangular sheet of paper 44 cm x 20 cm, is rolled along its length to form a cylinder. Find the volume of the cylinder so formed.
Solution:
Size of sheet of paper = 44 cm x 20 cm
By rolling along length, a cylinder is formed in which circumference of its base = 20 cm
and height (h) = 44 cm

Question 11.
The volume and the curved surface area of a cylinder are 1650 cm3 and 660 cm2 respectively. Find the radius and height of the cylinder.
Solution:
Volume of cylinder = 1650 cm³
and curved surface area = 660 cm²
Let r be the radius and h be the height of the cylinder, then

Question 12.
The radii of two cylinders are in the ratio 2 :3 and their heights are in the ratio 5 : 3. Calculate the ratio of their volumes.
Solution:
Ratio in radii = 2:3
and in heights = 5:3
Let r₁,h₁ and r₂, h₂ are the radii and heights of two cylinders respectively.

Question 13.
The ratio between the curved surface area and the total surface area of a right circular cylinder is 1 : 2. Find the volume of the cylinder, if its total surface area is 616 cm².
Solution:
Ratio in curved surface are and total surface area =1 : 2
Let r be the radius and h be the height.
Then 2πrh : 2πr (h + r)= 1 : 2

Question 14.
The curved surface area of a cylinder is 1320 cm2 and its base has diameter 21 cm. Find the volume of the cylinder.
Solution:
Curved surface area of a cylinder = 1320 cm²
Diameter of base = 21 cm

Question 15.
The ratio between the radius of the base and the height of a cylinder is 2 : 3. Find the total surface area of the cylinder, if its volume is 1617 cm³.
Solution:
Ratio between radius and height of a cylinder = 2:3
Volume = 1617 cm³
Let r be the radius and A be the height of the cylinder, then

Question 16.
The curved surface area of a cylindrical pillar is 264 m² and its volume is 924 m³. Find the diameter and the height of the pillar.
Solution:
Let r be the radius and A be the height of the cylinder, then
2πrh = 264 …(i)
and πr2h= 924 …(ii)
Dividing (ii) by (i),

Question 17.
Two circular cylinders of equal volumes have their heights in the ratio 1 : 2. Find the ratio of their radii.
Solution:
Volumes of two cylinders are equal.
Let r1, r2 are the radii and h₁, h₂ are their heights, then

Now, volume of first cylinder = πr₁²h₁
and Volume of second cylinder = πr₂²h₂
Their volumes are equal

Question 18.
The height of a right circular cylinder is 10.5 m. Three times the sum of the areas of its two circular faces is twice the area of the curved surface. Find the volume of the cylinder.
Solution:
Height of cylinder (A) = 10.5 m.
Let r be the radius, then
Sum of areas of two circular faces = 2π²
and curved surface area = 2πrh
According to the condition,

Question 19.
How many cubic metres of earth must be dug-out to sink a well 21 m deep and 6 m diameter ?
Solution:
Diameter of well = 6 m

Question 20.
The trunk of a tree is cylindrical and its circumference is 176 cm. If the length of the trunk is 3 m, find the volume of the timber that can be obtained from the trunk.
Solution:
Circumference of cylindrical trunk = 176 cm

Question 21.
A well is dug 20 m deep and it has a diameter of 7 m. The earth which is so dug out is spread out on a rectangular plot 22 m long and 14 m broad, what is the height of the platform so formed ?
Solution:
Diameter of the well = 7 m
∴ Radius (r) = \(\frac { 7 }{ 2 }\) m
Depth (h) = 20 m
= Volume of earth dug out = πr²h

Question 22.
A well with 14 m diameter is dug 8 m deep. The earth taken out of it has been evenly spread all around it to a width of 21 m to form an embankment. Find the height of the embankment.
Solution:
Diameter of the well = 14 m

Question 23.
A cylindrical container with diameter of base 56 cm contains sufficient water to submerge a rectangular solid of iron with dimensions 32 cm x 22 cm x 14 cm. Find the rise in the level of the water when the solid is completely submerged.
Solution:
Diameter of the base of a cylindrical container = 56 cm

Dimensions of the rectangular solid = 32 cm x 22 cm x 14 cm
∴ Volume of solid = 32 x 22 x 14 cm³ = 9856 cm³
∴Volume of water rose up = 9856 cm³
Let h be the height of water, then πr²h = 9856

Question 24.
A rectangular sheet of paper 30 cm x 18 cm can be transformed into the curved surface of a right circular cylinder in two ways Le., either by rolling the paper along its length or by rolling it along its breadth. Find the ratio of the volumes of the two cylinders thus formed.
Solution:
Size of paper = 30 cm and 18 cm.

(i) By rolling length wise,
The circumference of base = 30 cm

Question 25.
The rain which falls on a roof 18 m long and 16.5 m wide is allowed to be stored in a cylindrical tank 8 m in diameter. If it rains 10 cm on a day, what is the rise of water level in the tank due to it.
Solution:
Length of roof (l) = 18 m
Breadth (b) = 16.5 m
Height of water on the roof = 10 cm
∴ Volume of water collected

Question 26.
A Piece of ductile metal is in the form of a cylinder of diameter 1 cm and length 5 cm. It is drawnout into a wire of diameter 1 mm. What will be the length of the wire so formed ?
Solution:
Diameter of ductile metal = 1 cm
and length (h) = 5 cm
and radius (r) = \(\frac { 1 }{ 2 }\) cm

Question 27.
Find the length of 13.2 kg of copper wire of diameter 4 mm when 1 cubic cm of copper weighs 8.4 gm.
Solution:
Weight of wire = 13.2 kg
Diameter of wire = 4 mm

Question 28.
2.2 cubic dm of brass is to be drawn into a cylindrical wire 0.25 cm in diameter. Find the length of the wire.
Solution:
Volume of brass = 2.2 cu.dm
= 2.2 x 10 x 10 x 10 = 2200 cm²
Diameter of wire = 0.25 cm

Question 29.
The difference between inside and outside surfaces of a cylindrical tube 14 cm long is 88 sq. cm. If the volume of the tube is 176 cubic cm, find the inner and outer radii of the tube.
Solution:
Let r and R be the radii of inner and outer surfaces of a cylindrical tube,

Question 30.
Water flows out through a circular pipe whose internal diameter is 2 cm, at the rate of 6 metres per second into a cylindrical tank, the radius of whose base is 60 cm. Find the rise in the level of water in 30 minutes.
Solution:
Diameter of pipe = 2 cm
∴ Radius (r) = \(\frac { 2 }{ 2 }\) = 1 cm = 0.01 m
Length of flow of water in 1 second = 6 m Length of flow in 30 minutes = 6 x 30 x 60 m = 10800 m
∴ Volume of water = πr²h

Question 31.
A cylindrical tube, open at both ends, is to made of metal. The internal diameter of the tube is 10.4 cm and its length is 25 cm. The thickness of the metal tube is 8 mm everywhere. Calculate the volume of the metal.
Solution:
Length of metal tube (h) = 25 cm
Internal diameter = 10.4 cm
∴ Internal radius (r) = \(\frac { 10.4 }{ 2 }\) = 5.2 cm
Thickness of metal = 8 mm = 0.8 cm
∴ Outer radius = 5.2 + 0.8 = 6 cm
Now volume of the metal

Question 32.
From a tap of inner radius 0.75 cm, water flows at the rate of 7 m per second. Find the volume in litres of water delivered by the pipe in one hour.
Solution:
Inner radius of pipe (r) = 0.75 cm
Rate of water flow = 7 m per second
∴ Length of water flow in 1 hour (h)
= 7 x 3600 m = 25200 m
∴ Volume of water in 1 hour

Question 33.
A cylindrical water tank of diameter 1. 4 m and height 2.1 m is being fed by a pipe of diameter 3.5 cm through which water flows at the rate of 2 metre per second. In how much time the tank will be filled ?
Solution:
Diameter of cylindrical tank = 1.4 m
∴ Radius (r) = \(\frac { 1.4 }{ 2 }\) = 0.7 m
Height (h) = 2.1m.

Question 34.
A rectangular sheet of paper 30 cm x 18 cm can be transformed into the curved surface of a right circular cylinder in two ways Le. either by rolling the paper along its length or by rolling it along its breadth. Find the ratio of the volumes of the two cylinder thus formed.
Solution:
In first case,
By rolling the paper along its length,
the circumference of the base = 30 cm
and height (h) = 18 cm

Note: See Q.No. 24 this exercise

Question 35.
How many litres of water flow out of a pipe having an area of cross-section of 5 cm2 in one minute, if the speed of water in the pipe is 30 cm/sec ?
Solution:
Speed of water = 30 cm/sec
∴ Water flow in 1 minute = 30 cm x 60 = 1800 cm
Area of cross-section = 5 cm²
∴ Volume of water = 1800 x 5 = 9000 cm³
Capacity of water in litres = 9000 x l ml

Question 36.
A solid cylinder has a total surface area of 231 cm². Its curved surface area is \(\frac { 2 }{ 3 }\) of the total surface area. Find the volume of the cylinder.
Solution:
Total surface area of a solid cylinder = 231 cm²
Curved surface area = \(\frac { 2 }{ 3 }\) of 231 cm² = 2 x 77 = 154 cm²
and area of two circular faces = 231-154 = 77 cm²
Let r be the radius, then

Question 37.
Find the cost of sinking a tubewell 280 m deep, having diameter 3 m at the rate of Rs 3.60 per cubic metre. Find also the cost of cementing its inner curved surface at Rs 2.50 per square metre.
Solution:
Diameter of well = 3 m
∴ Radius (r) = \(\frac { 3 }{ 2 }\) m
and depth (h) = 280 m
(i) Volume of earth dug out = πr²h

Rate of sinking the well = Rs 3.60 per m³
∴ Total cost of sinking = Rs 1980 x 3.60 = Rs 7,128
(ii) Inner curved surface area = 2πrh

Rate of cementing = Rs 2.50 per m²
∴ Total cost of cementing = Rs 2.50 x 2640
= Rs 6,600

Question 38.
Find the length of 13.2 kg of copper wire of diameter 4 mm, when 1 cubic cm of copper weighs 8.4 gm.
Solution:
Note : See Q.No. 27 of this exercise

Question 39.
2.2 cubic dm of brass is to be drawn into a cylindrical wire 0.25 cm in diameter. Find the length of the wire.
Solution:
Note: See Q.No. 28 of this exercise.

Question 40.
A well with 10 m inside diameter is dug 8.4 m deep. Earth taken out of it is spread all around it to a width of 7.5 m to form an embankment. Find the height of the embankment.
Solution:
Diameter of the well = 10 m

Question 41.
A hollow garden roller, 63 cm wide with a girth of 440 cm, is made of 4 cm thick iron. Find the volume of the iron.
Solution:
Width of roller (h) = 63 cm.

Outer circumference of roller = 440 cm

Question 42.
What length of a solid cylinder 2 cm in diameter must be taken to recast into a hollow cylinder of length 16 cm, external diameter 20 cm and thickness 2.5 mm ?
Solution:
Length of hollow cylinder (h) = 16 cm
External diameter = 20 cm
∴ External radius (R) = \(\frac { 20 }{ 2 }\) = 10 cm
Thickness of iron = 2.5 mm
∴ Internal radius (r) = 10 – 0.25 = 9.75 cm
∴ Volume of iron = πh (R² – r²)

Question 43.
In the middle of rectangular field measuring 30 m x 20 m, a well of 7 m diameter and 10 m depth is dug. The earth so removed is evenly spread over the remaining part of the field. Find the height through which the level of the field is raised.
Solution:
Diameter of well = 7 m
∴ Radius (r) = \(\frac { 7 }{ 2 }\) m
Depth (h) = 10 m.
∴ Volume of earth dug out = πr²h

Hope given RD Sharma Class 8 Solutions Chapter 22 Mensuration III Ex 22.2 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 8 Solutions Chapter 22 Mensuration III (Surface Area and Volume of a Right Circular Cylinder) Ex 22.1

These Solutions are part of RD Sharma Class 8 Solutions. Here we have given RD Sharma Class 8 Solutions Chapter 22 Mensuration III Ex 22.1

Other Exercises

• RD Sharma Class 8 Solutions Chapter 22 Mensuration III Ex 22.1
• RD Sharma Class 8 Solutions Chapter 22 Mensuration III Ex 22.2

Question 1.
Find the curved surface area and total surface area of a cylinder, the diameter of whose base is 7 cm and height is 60 cm.
Solution:
Diameter of the base of cylinder = 7 cm
∴ Radius (r) = \(\frac { 7 }{ 2 }\) cm
Height (h) = 60m
∴ carved surface area = 2πh
= 2 x \(\frac { 22 }{ 7 }\) x \(\frac { 7 }{ 2 }\) x 60cm² = 1320cm²

Question 2.
The curved surface area of a cylindrical road is 132 cm2. Find its length if the radius is 0.35 cm.
Solution:
Curved surface area =132 cm²
Radius (r) = 0.35 cm
Let h be the length of the rod Then 2πrh = 132

Question 3.
The area of the base of a right circular cylinder is 616 cm2 and its height is 2.5 cm. Find the curved surface area of the cylinder.
Solution:
Let r be the radius of the base of the cylinder, then
Area of the base = πr²

Question 4.
The circumference of the base of a cylinder is 88 cm and its height is 15 cm. Find its curved surface area and total surface area.
Solution:
Height of the cylinder (h) = 15 cm
Circumference of the base = 88 cm
Let r be the radius of the base, the circumference = 2πr
∴ 2πr = 88 cm …(i)

Question 5.
A rectangular strip 25 cm x 7 cm is rotated about the longer side. Find the total surface area of the solid thus generated.
Solution:
Dimensions of rectangular strip = 25 cm x 7 cm
By rotating the strip along longer side, a solid is formed whose radius = 7 cm
and height = 25 cm

Question 6.
A rectangular sheet of paper 44 cm x 20 cm, is rolled along its length to form a cylinder. Find the the total surface area of the cylinder thus generated.
Solution:
By rolling along length wire, we get a cylinder whose circumference of its base = 20 cm

Question 7.
The radii of two cylinders are in the ratio of 2 : 3 and their heights are in the ratio 5 : 3. Calculate the ratio of their curved surface areas.
Solution:
Ratio in radii of two cylinders = 2:3
and ratio in their heights = 5:3

Question 8.
The ratio between the curved surface area and the total surface area of a right circular cylinder is 1: 2. Prove that its height and radius are equal.
Solution:
Let r be the radius and h be the height of a right circular cylinder, then Curved surface area = 2πrh
and total surface area = 2πrh x 2πr² = 2πr (h + r)
But their ratio is 1 : 2

Hence their radius and height are equal.

Question 9.
The curved surface area of a cylinder is 1320 cm² and its base has diameter 21 cm. Find the height of the cylinder.
Solution:
Curved surface area of a cylinder = 1320 cm²
Diameter of its base (d) = 21 cm 21
Radius (r) = \(\frac { 21 }{ 2 }\) cm
Let h be the height of the cylinder

Question 10.
The height of a right circular, cylinder is 10.5 m. If three times the sum of the areas of its two circular faces is twice the area of the curved surface area. Find the radius of its base.
Solution:
Height of cylinder = 10.5 m
Let r be the radius and h be the height of a right circular cylinder, then Area of its two circular faces = 2π²
and area of curved surface = 2πrh
Now, according to the condition:

Question 11.
Find the cost of plastering the inner surface of a well at Rs 9.50 per m2, if it is 21 m deep and diameter of its top is 6 m.
Solution:
Diameter of the top of a cylindrical well = 6m

∴ Radius (r) = \(\frac { 6 }{ 2 }\) = 3 m
and depth (h) = 21 m
∴ Curved surface area = 2πrh = 2 x \(\frac { 22 }{ 7 }\) x 3 x 21 m² = 396 m²
Rate of plastering = Rs 9.50 per m²
∴ Total cost of plastering = Rs 9.50 x 396 = Rs 3,762

Question 12.
A cylindrical vessel open at the top has diameter 20 cm and height 14 cm. Find the cost of the tin-plating it on the inside at the rate of 50 paise per hundred square centimetre.
Solution:
Diameter of the vessel = 20 cm

Question 13.
The inner diameter of a circular well is 3.5 m. It is 10 m deep. Find the cost of plastering its inner curved surface at Rs 4 per square metre.
Solution:
Diameter of the well = 3.5 m

Question 14.
The diameter of a roller is 84 cm and its length is T20 cm. It takes 500 complete revolutions moving once over to level a playground. What is the area of the playground ?
Solution:
Diameter of the roller = 84 cm

Question 15.
Twenty cylindrical pillars of the Parliament House are to be cleaned. If the diameter of each pillar is 0.50 m and height is 4 m, what will be the cost of cleaning them at the rate of Rs 2.50 per square metre ?
Solution:
Diameter of each pillar = 0.50 m

Question 16.
The total surface area of a hollow cylinder which is open from both sides is 4620 sq. cm, area of the base ring is 115.5 sq. cm and height 7 cm. Find the thickness of the cylinder.
Solution:
Total surface area of a hollow cylinder opened from both sides = 4620 cm²
Area of base ring = 115.5 cm²
Height of cylinder (h) = 7 cm
Let R be the outer radius and r be the inner radius

Question 17.
The sum of the radius of the base and height of a solid cylinder is 37 m, if the total surface area of the solid cylinder is 1628 m², find the circumference of its base.
Solution:
Let r be the radius and h be the height of the solid cylinder, then r + h = 37 m …(i)
Total surface area = 1628
⇒ 2πr (r + h) = 1628

Question 18.
Find the ratio between the total surface area of a cylinder to is curved surface area,given that its height and radius are 7.5 cm and 3.5 cm.
Solution:
Radius (r) of cylinder = 3.5 cm
and height (h) = 7.5 cm
∴ Curved surface area = 2πrh
and total surface area = 2πr (h + r)
∴ Ratio = 2πr (h + r)- 2πrh = (h + r): h = 7.5 + 3.5 : 7.5
⇒ 11 : 7.5

Question 19.
A cylindrical vessel, without lid, has to be tin-coated on its both sides. If the radius of the base is 70 cm and its height is 1.4 m, calculate the cost of tin-coating at the rate of Rs 3.50 per 1000 cm².
Solution:
Radius of the vessel (r) = 70 cm
and height (h) = 1.4 m = 140 cm
∴ Area of inner and outer curved surfaces and bases = 2 x 2πrh + 2πr²

Hope given RD Sharma Class 8 Solutions Chapter 22 Mensuration III Ex 22.1 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 8 Solutions Chapter 23 Data Handling I Ex 23.2

These Solutions are part of RD Sharma Class 8 Solutions. Here we have given RD Sharma Class 8 Solutions Chapter 23 Data Handling I Ex 23.2

Other Exercises

• RD Sharma Class 8 Solutions Chapter 23 Data Handling I Ex 23.1
• RD Sharma Class 8 Solutions Chapter 23 Data Handling I Ex 23.2

Question 1.
The marks obtained by 40 students of class VIII in an examination are given below :
16, 17, 18, 3, 7, 23, 18, 13, 10, 21, 7, 1, 13,
21, 13, 15, 19, 24, 16, 3, 23, 5, 12, 18, 8, 12, 6,
8, 16, 5, 3, 5, 0, 7, 9, 12, 20, 10, 2, 23.
Divide the data into five groups, namely 0-5,5-10,10-15,15-20 and 20-25 and prepare a grouped frequency table.
Solution:
Frequency distribution table

Question 2.
The marks scored by 20 students in a test are given below :
54, 42, 68, 56, 62, 71, 78, 51, 72, 53, 44, 58, 47, 64, 41, 57, 89, 53, 84, 57.
Complete the following frequency table :

What is the class interval in which the greatest frequency occurs ?
Solution:

The class in which the greatest frequency is 50-60

Question 3.
The following is the distribution of weights (in kg) of 52 persons :


(i) What is the lower limit of class 50-60 ?
(ii) Find the class marks of the classes 40-50, 50-60.
(iii) What is the class size ?
Solution:
(i) Lower limit of class 50-60 = 50
(ii) Class marks of 40-50 = \(\frac { 40+50 }{ 2 }\) = \(\frac { 90 }{ 2 }\)
= 45 and of 50-60 = \(\frac { 50+60 }{ 2 }\) = \(\frac { 110 }{ 2 }\) =55
(iii) Class size is 10

Question 4.
Construct a frequency table for the following weights (in gm) of 35 mangoes using the equal class intervals, one of them is 40-45 (45 not included):
30,40,45,32,43,50,55,62,70,70,61,62, 53,52, 50,42,35,37,53,55,65,70, 73, 74,45, 46, 58, 59, 60, 62, 74, 34, 35, 70 ,68.
(i) What is the class mark of the class interval 40-45 ?
(ii) What is the range of the above weights ?
(iii) How many classes are there ?
Solution:
Smallest observation = 30
Greatest observation = 74
Range = 74 – 30 = 44
Now forming the distribution table

(i) Class mark of 40-45
= \(\frac { 40+45 }{ 2 }\) = \(\frac { 85 }{ 2 }\) = 42.5
(ii) Range = 74 – 30 = 44
(iii) Number of classes are 9

Question 5.
Construct a frequency table with class-intervals 0-5 (5 not included) of the following marks obtained by a group of 30 students in an examination :
0, 5, 7,10, 12,15, 20, 22, 25, 27, 8, 11, 17,3, 6, 9,17,19, 21, 29, 31,35,37,40,42, 45, 49, 4, 50, 16.
Solution:
Frequency distribution table.

Question 6.
The marks scored by 40 students of class VIII in mathematics are given below:
81,55, 68, 79,85,43,29,68,54,73,47, 35, 72,64,95,44,50, 77,64,35,79, 52, 45,54,70,83, 62′, 64,72,92,84,76,63, 43, 54, 38, 73, 68, 52, 54.
Prepare a frequency distribution with class size of 10 marks.
Solution:
Largest marks = 95
Lowest marks = 29
Range = 95 – 29 = 66
Frequency distribution table

Question 7.
The heights (in cm) of 30 students of class VIII are given below :
155.158.154.158.160.148.149.150.153, 159,161,148,157,153,157,162,159,151, 154,156,152,156,160,152,147,155,163,155,157,153.
Prepare a frequency distribution table with 160-164 as one of the class intervals.
Solution:
Largest height =163
Lowest height =147
Range = 163- 147 = 16

Question 8.
The monthly wages of 30 workers in a factory are given below :
830,835,890,810,835,836,869,845,898, 890, 820, 860, 832, 833, 855, 845, 804, 808, 812, 840, 885, 835, 836, 878, 840, 868, 890, 806, 840, 890.
Represent the data in the form of a frequency distribution with class size 10.
Solution:
Highest wage = 898
Lowest wage = 804
Range = 898 – 804 = 94
Frequency distribution table

Question 9.
Construct a frequency table with equal class intervals from the following data on the monthly wages (in rupees) at 28 labourers working in a factory, taking one of the class intervals as 210-230 (230 not included):
220, 268, 258, 242, 210, 268, 272,242, 311, 290, 300, 320,319,304,302,318,306,292, 254, 278, 210,240, 280,316,306, 215, 256, 236.
Solution:
Highest wages = 320
Lowest wages = 210
Range = 320-210= 110
Frequency distribution table

Question 10.
The daily minimum temperatures in degrees Celsius recorded in a certain Arctic region are as follows :
-12.5, -10.8, -18.6, -8.4, -10.8, -4.2, -4.8, -6.7, -13.2, -11.8, -2.3,1.2, 2.6, 0, -2.4, 0, 3.2, 2.7,3.4,0, -2.4, -2.4, 0,3.2, 2.7,3.4, 0,2.4, -5.8, -8.9, -14.6, -12.3, -11.5, -7.8, – 2.9
Represent them as frequency distribution table taking -19.9 to -15 as the first class interval.
Solution:
Lowest temperature = -19.9
Highest temperature = 3.4
Frequency distribution table

Hope given RD Sharma Class 8 Solutions Chapter 23 Data Handling I Ex 23.2 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 8 Solutions Chapter 23 Data Handling I (Classification and Tabulation of Data) Ex 23.1

These Solutions are part of RD Sharma Class 8 Solutions. Here we have given RD Sharma Class 8 Solutions Chapter 23 Data Handling I Ex 23.1

Other Exercises

• RD Sharma Class 8 Solutions Chapter 23 Data Handling I Ex 23.1
• RD Sharma Class 8 Solutions Chapter 23 Data Handling I Ex 23.2

Question 1.
Define the following terms :
(i) Observations
(ii) Raw data
(iii) Frequency of an observation
(iv) Frequency distribution
(v) Discrete frequency distribution
(vi) Grouped frequency distribution
(vii) Class-interval
(viii) Class-size
(ix) Class limits
(x) True class limits
Solution:
(i) Observations : Each entry in the given data is called an observation. ‘
(ii) Raw data: A collection of observations by an observer, is called raw data.
(iii) Frequency of an observation : The number of times an observation occurs in the given data is called its frequency.
(iv) Frequency distribution : The presentations of given data in order of magnitude ascending or descending, is called the frequency distribution.
(v) Discrete frequency distribution: When the given data is represented by tally marks after arranging it in an order. This kind of distribution is called discrete frequency distribution.
(vi) Grouped frequency distribution: If the number of data is large, and the difference between the greatest and the smallest observation is large, then we represent then in groups or classes. Such representation of data is called grouped frequency distribution.
(vii) Class intervals: The difference between the upper limit and lower limit of a class is called class interval.
(viii) Class-size : Class intervals are also called the class size. Each size of the same intervals
(ix) Class limits : Every class has two limits : upper limit and lower limit.
(x) True class limits or Exclusive limits : When the upper limit of one is the lower limit of the next interval then these are call true class limits.

Question 2.
The final marks in mathematics of 30 students are as follows :
53, 61, 48, 60, 78, 68, 55, 100, 67, 90, 75, 88,77,37,84,58,60,48,62,56,44,58,52,64, 98, 59, 70, 39, 50, 60
(i) Arrange these marks in the ascending order, 30 to 39 one group, 40 to 49 second group etc.
Now answer the following:
(ii) What is the highest score ?
(iii) What is the lowest score ?
(iv) What is the range ?
(v) If 40 is the pass mark how many have failed ?
(vi) How many have scored 75 or more ?
(vii) Which observations between 50 and 60 have not actually appeared ?
(viii) How many have scored less than 50 ?
Solution:
(i) Arranging the given data in ascending order.
30 to 39 : 37,39
40 to 49 : 44, 48, 48
50 to 59 : 50, 52, 53, 55, 56, 58, 58, 59
60 to 69 : 60, 60, 60, 61, 62, 64, 67, 68
70 to 79 : 70, 75, 77, 78
80 to 89 : 84, 88
90 to 99 : 90, 98
100 to 109 : 100
(ii) Highest score is 100
(iii) Lowest score is 37
(iv) Range is 100 – 37 = 63
(v) If 40 is pass marks then number of failed candidates will be = 2
(vi) Number of students who scored 75 or more = 8
(vii) Between 50 and 60, the observations 51, 54, 57 do not appear.
(viii) Number of students who scored less than 50 = 5

Question 3.
The weights of new born babies (in kg) in a hospital on a particular day are as follows:
2.3, 2.2, 2.1, 2.7, 2.6,3.0, 2.5, 2.9, 2-8,3.1, 2.5, 2.8, 2.7, 2.9, 2.4.
(i) Rearrange the weights in descending order.
(ii) Determine the highest weight:
(iii) Determine the lowest weight.
(iv) Determine the range.
(v) How many babies were born on that day?
(vi) How many babies weigh below 2.5 kg ?
(vii) How many babies weigh more than 2.8 kg ?
(viii) How many babies weigh 2.8 kg ?
Solution:
(i) Arranging the given weights in descending order.
3.1, 3.0, 2.9, 2.9, 2.8, 2.8, 2.7, 2.7, 2.6, 2.5, 2.5, 2.4, 2.3, 2.2, 2.1
(ii) Highest weight = 3.1 kg
(iii) Lowest weight = 2.1 kg
(iv) Range : 3.1 – 2.1 = 1 kg.
(v) Number of babies born on that day = 15
(vi) Number of babies having weight below 2.5 kg = 4
(vii) Number of babies having weight more than 2.8 kg = 4
(viii) Number of babies weigh 2.8 kg = 2

Question 4.
Following data gives the number of children in 41 families:
1,2,6,5,1,5,1,3,2,6,2,3,4,2,0,0,4,4, 3, 2, 2, 0, 0,1, 2, 2, 4,3, 2,1, 0, 5,1, 2,4, 3, 4, 1, 6, 2, 2.
Represent it in the form of a frequency distribution.
Solution:
Frequency distribution table

Question 5.
Prepare a frequency table of the following scores obtained by 50 students in a test:
42, 51, 21, 42, 37. 37, 42, 49, 38, 52, 7, 33, 17, 44, 39, 7, 14, 27, 39, 42, 42, 62, 37, 39, 67, 51, 53, 53, 59, 41, 29, 38, 27, 31, 54,19, 53, 51, 22, 61, 42, 39, 59, 47, 33, 34, 16, 37, 57, 43
Solution:
Frequency distribution table

Question 6.
A die was thrown 25 times and following scores were obtained:
1,5,2,4,3,6,1,4,2,5,1,6,2,6,3,5,4,1, 3, 2, 3, 6,1, 5, 2
Prepare a frequency table of the scores.
Solution:
Frequency distribution table

Question 7.
In a study of number of accidents per day, the observations for 30 days were obtained as follows:
6,3,5,6,4,3, 2,5,4,2,4,2,1,2, 2,0,5,4,6,1,6,0, 5, 3, 6,1, 5, 5, 2, 6
Prepare a frequency distribution table.
Solution:
Frequency distribution table

Question 8.
Prepare a frequency table of the following ages (in years) of 30 students of class VIII in your school:
13,14,13,12,14,13,14,15,13,14,13,14, 16,12,14,13,14,15,16,13,14,13,12,17,13, 12,13,13,13,14
Solution:
Frequency distribution table

Question 9.
Following figures relate to the weekly wages (in Rs) of 15 workers in a factory :
300,250,200,250,200,150,350,200,250, 200,150, 300,150, 200, 250 Prepare a frequency table.
(i) What is the range in wages (in Rs) ?
(ii) How many workers are getting Rs 350 ?
(iii) How many workers are getting the minimum wages ?
Solution:
Frequency distribution table

(i) Range = 350- 150 = 200
(ii) Number of workers getting Rs 350 = 1
(iii) Number of workers getting minimum wages = 3

Question 10.
Construct a frequency distribution table for the following marks obtained by 25 students in a history test in class Vin of a school:
9,17,12, 20,9,18, 25,17,19,9,12,9,12, 18, 17,19, 20, 25, 9,12,17,19, 19, 20, 9
(i) What is the range of marks ?
(ii) What is the highest mark ?
(iii) Which mark is occurring more frequently ?
Solution:
Frequency distribution table

(i) Range = 25 – 9 = 16
(ii) Highest marks = 25
(iii) Marks occurring more frequently = 9

Hope given RD Sharma Class 8 Solutions Chapter 23 Data Handling I Ex 23.1 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.