Class 9 Maths RD Sharma Solutions

RD Sharma Class 9 Solutions Chapter 24 Measures of Central Tendency VSAQS

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 24 Measures of Central Tendency VSAQS

Other Exercises

• RD Sharma Class 9 Solutions Chapter 24 Measures of Central Tendency Ex 24.1
• RD Sharma Class 9 Solutions Chapter 24 Measures of Central Tendency Ex 24.2
• RD Sharma Class 9 Solutions Chapter 24 Measures of Central Tendency Ex 24.3
• RD Sharma Class 9 Solutions Chapter 24 Measures of Central Tendency Ex 24.4
• RD Sharma Class 9 Solutions Chapter 24 Measures of Central Tendency VSAQS
• RD Sharma Class 9 Solutions Chapter 24 Measures of Central Tendency MCQS

Question 1.
If the ratio of mode and median of a certain data is 6 : 5, then find the ratio of its mean and median.
Solution:
We know that
Mode = 3 median – 2 mean…(i)
and \(\frac { mode }{ median } \) = \(\frac { 6 }{ 5 } \)
Mode = \(\frac { 6 }{ 5 } \)median
∴From (i), \(\frac { 6 }{ 5 } \) median = 3 median – 2 mean
=> 2 mean = 3 median – \(\frac { 6 }{ 5 } \)median
2 mean = \(\frac { 15-6 }{ 5 } \)median = \(\frac { 9 }{ 5 } \)median
\(\frac { mean }{ median } \) = \(\frac { 9 }{ 5X2 } \) = \(\frac { 9 }{ 10 } \)
∴Ratio = 9:10

Question 2.
If the mean of x + 2, 2x + 3, 3x + 4, 4x + 5 is x + 2, find x.
Solution:
Mean of x + 2, 2x + 3, 3x + 4, 4x + 5 = x + 2
=> \(\frac { x + 2+2x + 3+3x + 4+4x + 5 }{ 4 } \) = x + 2
=> 10x + 14 = 4x + 8
=> 10x – 4x = 8 – 14
=> 6x= – 6
∴ x = – 1

Question 3.
If the median of scores ,\(\frac { x }{ 2 } \), \(\frac { x }{ 3 } \), \(\frac { x }{ 4 } \), \(\frac { x }{ 5} \) and \(\frac { x }{ 6 } \) (where x > 0) is 6, then find the value \(\frac { x }{ 6 } \)
Solution:
\(\frac { x }{ 2 } \), \(\frac { x }{ 3 } \), \(\frac { x }{ 4 } \), \(\frac { x }{ 5} \), \(\frac { x }{ 6 } \)
Here n = 5
Median = \(\frac { n+1 }{ 2 } \) th term = \(\frac { 5+1 }{ 2 } \) th
\(\frac { 6 }{ 2 } \) = 3rd term = \(\frac { x }{ 4 } \)
\(\frac { x }{ 4 } \) = 6 => x = 24
\(\frac { x }{ 6 } \) = \(\frac { 24 }{ 6 } \) = 4
∴Hence = \(\frac { x }{ 6 } \) = 4

Question 4.
If the mean of 2, 4, 6, 8, x, y is 5, then find the value of x + y.
Solution:
Mean of 2, 4, 6, 8, x, y is 5
\(\frac { 2+4+6+8+x+y }{ 6 } \) = 5
\(\frac { 20+x+y }{ 6 } \) = 5
=> 20 + (x +y) = 30
=> x + y = 30 – 20 = 10
∴x + y = 10

Question 5.
If the mode of scores 3, 4, 3, 5, 4, 6, 6, x is 4, find the value of x.
Solution:
Mode of 3, 4, 3, 5, 4, 6, 6, x is 4
∴ 4 comes in maximum times
But here ,
3 2
4 2
5 1
6 2
3, 4 and 6 are equal in number
∴ x must be 4 so that it becomes in maximum times

Question 6.
If the median of 33, 28, 20. 25, 34, x is 29. find the maximum possible value of x.
Solution:
Median of 33, 28, 20, 25, 34, x is 29
Now arranging in ascending order 20, 25, 28, x, 33, 34
Here n = 6
Median = \(\frac { 1 }{ 2 } \left[ \frac { 6 }{ 2 } th\quad term+\left( \frac { 6 }{ 2 } +1 \right) th\quad term \right] \)
29 = \(\frac { 1 }{ 2 } \) [3rd term + 4th term]
29 = \(\frac { 1 }{ 2 } \) [28+x]
58 = 28 + x
=> x = 58 – 28 = 30
∴Possible value of x = 30

Question 7.
If the median of the scores 1, 2, x, 4, 5 (where 1 <2 <x <4 <5) is 3, then find the mean of the scores.
Solution:
Scores are 1, 2, x, 4, 5 and median 3
Here n = 5 which is odd
Median = \(\frac { n+1 }{ 2 } \) th term = \(\frac { 5+1 }{ 2 } \) = \(\frac { 6 }{ 2 } \) th
=> 3 = 3rd term = x
=> 3 = x
∴ x = 3
Mean of the score = \(\frac { 1+2+3+4+5 }{ 5 } \) = 3

Question 8.
If the ratio of mean and median of a certain data is 2 : 3, then find the ratio of its mode and mean.
Solution:
We know that mode = 3 median – 2 mean

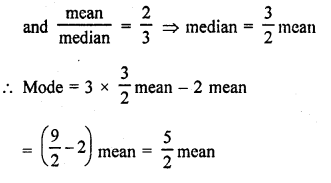
\(\frac { mode }{ mean } \) = \(\frac { 5 }{ 2 } \)
Ratio in mode and mean = 5 : 2

Question 9.
The arithmetic mean and mode of a data are 24 and 12 respectively, then find the median of the data.
Solution:
Mean = 24
Mode = 12
We know that mode = 3 median – 2 mean
12 = 3 median – 2 x 24
12 = 3 median – 48
3 median 12 + 48 = 60
Median = \(\frac { 60 }{ 3 } \) = 20

Question 10.
If the difference of mode and median of a data is 24, then find the difference of median and mean.
Solution:
Mode – Median = 24
Mode = 24 + median
But mode = 3 median – 2 mean
3 median – 2 mean = 24 + median
3 median – median – 2 mean = 24
=> 2 median – 2 mean = 24
=> Median – Mean = 12 (Dividing by 2)

Hope given RD Sharma Class 9 Solutions Chapter 24 Measures of Central Tendency VSAQS are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 9 Solutions Chapter 24 Measures of Central Tendency Ex 24.4

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 24 Measures of Central Tendency Ex 24.4

Other Exercises

• RD Sharma Class 9 Solutions Chapter 24 Measures of Central Tendency Ex 24.1
• RD Sharma Class 9 Solutions Chapter 24 Measures of Central Tendency Ex 24.2
• RD Sharma Class 9 Solutions Chapter 24 Measures of Central Tendency Ex 24.3
• RD Sharma Class 9 Solutions Chapter 24 Measures of Central Tendency Ex 24.4
• RD Sharma Class 9 Solutions Chapter 24 Measures of Central Tendency VSAQS
• RD Sharma Class 9 Solutions Chapter 24 Measures of Central Tendency MCQS

Question 1.
Find out the mode of the following marks obtained by 15 students in a class:
Marks : 4, 6, 5, 7, 9, 8, 10, 4, 7, 6, 5, 9, 8, 7, 7.
Solution:
Marks obtained are in ascending order,
4, 4, 5, 5, 6, 6, 7, 7, 7, 7, 8, 8, 9, 9, 10
Here we see that 7 is the number which is maximum times i.e. 4 times
Mode = 7

Question 2.
Find the mode for the following data:
125, 175, 225, 125, 225, 175, 325, 125, 375, 225, 125
Solution:
Arranging in ascending order,
125, 125, 125, 125, 175, 175, 225, 225, 225, 325, 375
We see that, 125 is the number which is in maximum times
Mode = 125

Question 3.
Find the mode for the following series:
7.5, 7.3, 7.2, 7.2, 7.4, 7.7, 7.7, 7.5, 7.3, 7.2, 7.6, 7.2
Solution:
Arranging in ascending order,
7.2, 7.2, 7.2, 7.2, 7.3, 7.3, 7.4, 7.5, 7.5, 7.6, 7.7, 7.7
We see that 7.2 comes in maximum times
Mode = 7.2

Question 4.
Find the mode of the following data in each case:
(i) 14, 25, 14, 28, 18, 17, 18, 14, 23, 22, 14, 18
(ii) 7, 9, 12, 13, 7, 12, 15, 7, 12, 7, 25, 18, 7
Solution:
(i) 14, 25, 14, 28, 18, 17, 18, 14, 23, 22, 14, 18
Arranging in ascending order,
14, 14, 14,. 14, 17, 18, 18, 18, 22, 23, 25, 28
Here we see that 14 comes in maximum times
Mode = 14
(ii) 7, 9, 12, 13, 7, 12, 15, 7, 12, 7, 25, 18, 7
Arranging in order,
7, 7, 7, 7, 7, 9, 12, 12, 12, 13, 15, 18, 25
Here we see that 7 comes in maximum times
Mode = 7

Question 5.
The demand of different shirt sizes, as obtained by a survey, is given below:

Find the modal shirt sizes, as observed from the survey.
Solution:
From the given data

From above, we see that
Modal size is 39 as it has maximum times persons

Hope given RD Sharma Class 9 Solutions Chapter 24 Measures of Central Tendency Ex 24.4 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 9 Solutions Chapter 11 Co-ordinate Geometry Ex 11.1

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 11 Co-ordinate Geometry Ex 11.1

Other Exercises

• RD Sharma Class 9 Solutions Chapter 11 Co-ordinate Geometry Ex 11.1
• RD Sharma Class 9 Solutions Chapter 11 Co-ordinate Geometry Ex 11.2
• RD Sharma Class 9 Solutions Chapter 11 Co-ordinate Geometry VSAQS
• RD Sharma Class 9 Solutions Chapter 11 Co-ordinate Geometry MCQS

Question 1.
In a ∆ABC, if ∠A = 55°, ∠B = 40°, find ∠C.
Solution:
∵ Sum of three angles of a triangle is 180°
∴ In ∆ABC, ∠A = 55°, ∠B = 40°
But ∠A + ∠B + ∠C = 180° (Sum of angles of a triangle)

⇒ 55° + 40° + ∠C = 180°
⇒ 95° + ∠C = 180°
∴ ∠C= 180° -95° = 85°

Question 2.
If the angles of a triangle are in the ratio 1:2:3, determine three angles.
Solution:
Ratio in three angles of a triangle =1:2:3
Let first angle = x
Then second angle = 2x
and third angle = 3x
∴ x + 2x + 3x = 180° (Sum of angles of a triangle)
⇒6x = 180°
⇒x = \(\frac { { 180 }^{ \circ } }{ 6 }\)  = 30°
∴ First angle = x = 30°
Second angle = 2x = 2 x 30° = 60°
and third angle = 3x = 3 x 30° = 90°
∴ Angles are 30°, 60°, 90°

Question 3.
The angles of a triangle are (x – 40)°, (x – 20)° and (\(\frac { 1 }{ 2 }\) x – 10)°. Find the value of x.
Solution:
∵ Sum of three angles of a triangle = 180°
∴ (x – 40)° + (x – 20)° + (\(\frac { 1 }{ 2 }\)x-10)0 = 180°
⇒ x – 40° + x – 20° + \(\frac { 1 }{ 2 }\)x – 10° = 180°
⇒ x + x+ \(\frac { 1 }{ 2 }\)x – 70° = 180°
⇒ \(\frac { 5 }{ 2 }\)x = 180° + 70° = 250°
⇒ x = \(\frac { { 250 }^{ \circ }x 2 }{ 5 }\)  = 100°
∴ x = 100°

Question 4.
Two angles of a triangle are equal and the third angle is greater than each of those angles by 30°. Determine all the angles of the triangle.
Solution:
Let each of the two equal angles = x
Then third angle = x + 30°
But sum of the three angles of a triangle is 180°
∴ x + x + x + 30° = 180°
⇒ 3x + 30° = 180°
⇒3x = 150° ⇒x = \(\frac { { 150 }^{ \circ } }{ 3 }\) = 50°
∴ Each equal angle = 50°
and third angle = 50° + 30° = 80°
∴ Angles are 50°, 50° and 80°

Question 5.
If one angle of a triangle is equal to the sum of the other two, show that the triangle is a right triangle.
Solution:
In the triangle ABC,

∠B = ∠A + ∠C
But ∠A + ∠B + ∠C = 180°
⇒∠B + ∠A + ∠C = 180°
⇒∠B + ∠B = 180°
⇒2∠B = 180°
∴ ∠B = \(\frac { { 180 }^{ \circ } }{ 2 }\) = 90°
∵ One angle of the triangle is 90°
∴ ∆ABC is a right triangle.

Question 6.
Can a triangle have:
(i) Two right angles?
(ii) Two obtuse angles?
(iii) Two acute angles?
(iv) All angles more than 60°?
(v) All angles less than 60°?
(vi) All angles equal to 60°?
Justify your answer in each case.
Solution:
(i) In a triangle, two right-angles cannot be possible. We know that sum of three angles is 180° and if there are two right-angles, then the third angle will be zero which is not possible.
(ii) In a triangle, two obtuse angle cannot be possible. We know that the sum of the three angles of a triangle is 180° and if there are
two obtuse angle, then the third angle will be negative which is not possible.
(iii) In a triangle, two acute angles are possible as sum of three angles of a trianlge is 180°.
(iv) All angles more than 60°, they are also not possible as the sum will be more than 180°.
(v) All angles less than 60°. They are also not possible as the sum will be less than 180°.
(vi) All angles equal to 60°. This is possible as the sum will be 60° x 3 = 180°.

Question 7.
The angles of a triangle are arranged in ascending order of magnitude. If the difference between two consecutive angle is 10°, find the three angles.
Solution:
Let three angles of a triangle be x°, (x + 10)°, (x + 20)°
But sum of three angles of a triangle is 180°
∴ x + (x+ 10)° + (x + 20) = 180°
⇒ x + x+10°+ x + 20 = 180°
⇒ 3x + 30° = 180°
⇒ 3x = 180° – 30° = 150°
∴ x = \(\frac { { 180 }^{ \circ } }{ 2 }\) = 50°
∴ Angle are 50°, 50 + 10, 50 + 20
i.e. 50°, 60°, 70°

Question 8.
ABC is a triangle is which ∠A = 72°, the internal bisectors of angles B and C meet in O. Find the magnitude of ∠BOC.
Solution:
In ∆ABC, ∠A = 12° and bisectors of ∠B and ∠C meet at O

Now ∠B + ∠C = 180° – 12° = 108°
∵ OB and OC are the bisectors of ∠B and ∠C respectively
∴ ∠OBC + ∠OCB = \(\frac { 1 }{ 2 }\) (B + C)
= \(\frac { 1 }{ 2 }\) x 108° = 54°
But in ∆OBC,
∴ ∠OBC + ∠OCB + ∠BOC = 180°
⇒ 54° + ∠BOC = 180°
∠BOC = 180°-54°= 126°
OR
According to corollary,
∠BOC = 90°+ \(\frac { 1 }{ 2 }\) ∠A
= 90+ \(\frac { 1 }{ 2 }\) x 72° = 90° + 36° = 126°

Question 9.
The bisectors of base angles of a triangle cannot enclose a right angle in any case.
Solution:
In right ∆ABC, ∠A is the vertex angle and OB and OC are the bisectors of ∠B and ∠C respectively
To prove : ∠BOC cannot be a right angle
Proof: ∵ OB and OC are the bisectors of ∠B and ∠C respectively

∴ ∠BOC = 90° x \(\frac { 1 }{ 2 }\) ∠A
Let ∠BOC = 90°, then
\(\frac { 1 }{ 2 }\) ∠A = O
⇒∠A = O
Which is not possible because the points A, B and C will be on the same line Hence, ∠BOC cannot be a right angle.

Question 10.
If the bisectors of the base angles of a triangle enclose an angle of 135°. Prove that the triangle is a right triangle.
Solution:
Given : In ∆ABC, OB and OC are the bisectors of ∠B and ∠C and ∠BOC = 135°

To prove : ∆ABC is a right angled triangle
Proof: ∵ Bisectors of base angles ∠B and ∠C of the ∆ABC meet at O
∴ ∠BOC = 90°+ \(\frac { 1 }{ 2 }\)∠A
But ∠BOC =135°
∴ 90°+ \(\frac { 1 }{ 2 }\) ∠A = 135°
⇒ \(\frac { 1 }{ 2 }\)∠A= 135° -90° = 45°
∴ ∠A = 45° x 2 = 90°
∴ ∆ABC is a right angled triangle

Question 11.
In a ∆ABC, ∠ABC = ∠ACB and the bisectors of ∠ABC and ∠ACB intersect at O such that ∠BOC = 120°. Show that ∠A = ∠B = ∠C = 60°.
Solution:
Given : In ∠ABC, BO and CO are the bisectors of ∠B and ∠C respectively and ∠BOC = 120° and ∠ABC = ∠ACB

To prove : ∠A = ∠B = ∠C = 60°
Proof : ∵ BO and CO are the bisectors of ∠B and ∠C
∴ ∠BOC = 90° + \(\frac { 1 }{ 2 }\)∠A
But ∠BOC = 120°
∴ 90°+ \(\frac { 1 }{ 2 }\) ∠A = 120°
∴ \(\frac { 1 }{ 2 }\) ∠A = 120° – 90° = 30°
∴ ∠A = 60°
∵ ∠A + ∠B + ∠C = 180° (Angles of a triangle)
∠B + ∠C = 180° – 60° = 120° and ∠B = ∠C
∵ ∠B = ∠C = \(\frac { { 120 }^{ \circ } }{ 2 }\) = 60°
Hence ∠A = ∠B = ∠C = 60°

Question 12.
If each angle of a triangle is less than the sum of the other two, show that the triangle is acute angled.
Solution:
In a ∆ABC,
Let ∠A < ∠B + ∠C

⇒∠A + ∠A < ∠A + ∠B + ∠C
⇒ 2∠A < 180°
⇒ ∠A < 90° (∵ Sum of angles of a triangle is 180°)
Similarly, we can prove that
∠B < 90° and ∠C < 90°
∴ Each angle of the triangle are acute angle.

Hope given RD Sharma Class 9 Solutions Chapter 11 Co-ordinate Geometry Ex 11.1 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 9 Solutions Chapter 24 Measures of Central Tendency Ex 24.3

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 24 Measures of Central Tendency Ex 24.3

Other Exercises

• RD Sharma Class 9 Solutions Chapter 24 Measures of Central Tendency Ex 24.1
• RD Sharma Class 9 Solutions Chapter 24 Measures of Central Tendency Ex 24.2
• RD Sharma Class 9 Solutions Chapter 24 Measures of Central Tendency Ex 24.3
• RD Sharma Class 9 Solutions Chapter 24 Measures of Central Tendency Ex 24.4
• RD Sharma Class 9 Solutions Chapter 24 Measures of Central Tendency VSAQS
• RD Sharma Class 9 Solutions Chapter 24 Measures of Central Tendency MCQS

Find the median of the following data (1-8)

Question 1.
83, 37, 70, 29, 45, 63, 41, 70, 34, 54
Solution:
We know that median = \(\frac { 1 }{ 2 } \left[ \frac { n }{ 2 } th\quad term+\left( \frac { n }{ 2 } +1 \right) th\quad term \right] \)
(When n is even)
= \(\frac { n+1 }{ 2 } th\quad term\)
83, 37, 70, 29, 45, 63, 41, 70, 34, 54
Arranging in ascending order, 29, 34, 37, 41, 45, 54, 63, 70, 70, 83
Here n = 10 which an even
Median = \(\frac { 1 }{ 2 } \)[5th term + 6th term]
= \(\frac { 1 }{ 2 } \) (45+54) = \(\frac { 99 }{ 2 } \) = 49.5

Question 2.
133, 73, 89, 108, 94, 104, 94, 85, 100, 120
Solution:
133, 73, 89, 108, 94, 104, 94, 85, 100, 120
Arranging in ascending order, 73, 85, 89, 94, 94, 100, 104, 108, 120, 133
Here n = 10 which is an even
Median = \(\frac { 1 }{ 2 } \)[5th term + 6th term]
= \(\frac { 1 }{ 2 } \) (94+100) = \(\frac { 1 }{ 2 } \) x 194 = 97

Question 3.
31, 38, 27, 28, 36, 25, 35, 40
Solution:
31, 38, 27, 28, 36, 25, 35, 40
Arranging in ascending order, 25, 27, 28, 31, 35, 36, 38, 40
Here n = 8 which is even
Median = \(\frac { 1 }{ 2 } \)[4th term + 5th term]
= \(\frac { 1 }{ 2 } \) (31+35) = \(\frac { 1 }{ 2 } \) x 66 = 33

Question 4.
15, 6, 16, 8, 22, 21, 9, 18, 25
Solution:
15, 6, 16, 8, 22, 21, 9, 18, 25
Arranging in ascending order = 6, 8, 9, 15, 16, 18, 21, 22, 25
Here n = 9 which is odd
Median \(\frac { n+1 }{ 2 } th\quad term\) = \(\frac { 9+1 }{ 2 } th\quad term\) = \(\frac { 10 }{ 2 } th\quad \)
= 5th term = 16

Question 5.
41, 43, 127, 99, 71, 92, 71, 58, 57
Solution:
41, 43, 127, 99, 71, 92, 71, 58, 57
Arranging in ascending order = 41, 43, 57, 58, 71, 71, 92, 99, 127
Here n = 9 which is an odd
Median \(\frac { n+1 }{ 2 } th\quad term\) = \(\frac { 9+1 }{ 2 } th\quad term\) = \(\frac { 10 }{ 2 } th\quad\)
= 5th term = 71

Question 6.
25, 34, 31, 23, 22, 26, 35, 29, 20, 32
Solution:
25, 34, 31, 23, 22, 26, 35, 29, 20, 32
Arranging in ascending order = 20, 22, 23, 25, 26, 29, 31, 32, 34, 35
Here n = 10 which is even
Median = \(\frac { 1 }{ 2 } \left[ \frac { n }{ 2 } th\quad term+\left( \frac { n }{ 2 } +1 \right) th\quad term \right] \)
= \(\frac { 1 }{ 2 } \) [5th term + 6th term]
= \(\frac { 1 }{ 2 } \) (26 + 29) = \(\frac { 1 }{ 2 } \) x 55 = \(\frac { 55 }{ 2 } \) = 27.5

Question 7.
12, 17, 3, 14, 5, 8, 7, 15
Solution:
12, 17, 3, 14, 5, 8, 7, 15
Arranging in ascending order = 3, 5, 7, 8, 12, 14, 15, 17
Here n = 8 which is odd
Median = \(\frac { 1 }{ 2 } \left[ \frac { n }{ 2 } th\quad term+\left( \frac { n }{ 2 } +1 \right) th\quad term \right] \)
= \(\frac { 1 }{ 2 } \) [4th term + 5th term]
= \(\frac { 1 }{ 2 } \) (8+12) = \(\frac { 1 }{ 2 } \) x 20 = 10

Question 8.
92, 35, 67, 85, 72, 81, 56, 51, 42, 69
Solution:
92, 35, 67, 85, 72, 81, 56, 51, 42. 69
Arranging in ascending order = 35, 42, 51, 56, 67, 69, 72, 81, 85, 92
Here n = 10 which is even
Median = \(\frac { 1 }{ 2 } \left[ \frac { n }{ 2 } th\quad term+\left( \frac { n }{ 2 } +1 \right) th\quad term \right] \)
= \(\frac { 1 }{ 2 } \) [5th term + 6th term]
= \(\frac { 1 }{ 2 } \) (67+69) = \(\frac { 1 }{ 2 } \) x 136 = 68

Question 9.
Numbers 50, 42, 35, 2x + 10, 2x – 8, 12, 11, 8 are written in descending order and their median is 25, find x.
Solution:
50, 42, 35, 2x + 10, 2x – 8, 12, 11, 8 are in descending order
Here n = 8 which is even
Now Median = \(\frac { 1 }{ 2 } \left[ \frac { n }{ 2 } th\quad term+\left( \frac { n }{ 2 } +1 \right) th\quad term \right] \)
= \(\frac { 1 }{ 2 } \) [4th term + 5th term] = \(\frac { 1 }{ 2 } \)[2x + 10 + 2x – 8]
= \(\frac { 1 }{ 2 } \) [4x + 2] = 2x + 1
But median = 25
2x + 1 = 25
=> 2x = 25 – 1 = 24
=> \(\frac { 24 }{ 2 } \) = 12
Hence x = 12

Question 10.
Find the median of the following observations 46, 64, 87, 41, 58, 77, 35, 90, 55, 92, 33. If 92 is replaced by 99 and 41 by 43 in the above data, find the new median?
Solution:
46, 64, 87, 41, 58, 77, 35, 90, 55, 92, 33
Writing in ascending order = 33, 35, 41, 46, 55, 58, 64, 77, 87, 90, 92
Here n = 11 which is odd
Median = \(\frac { n+1 }{ 2 } \) th term
= \(\frac { 11+1 }{ 2 } \) = \(\frac { 12 }{ 2 } \)
= 6th term = 58
By replacing 92 by 93 and 41 by 43, then new order will be
33, 35, 43, 46, 55, 58, 64, 77, 87, 90, 99
Median = 6th term = 58

Question 11.
Find the median of the following data : 41, 43, 127, 99, 61, 92, 71, 58, 57. If 58 is replaced by 85, what will be the new median.
Solution:
41, 43, 127, 99, 61, 92, 71, 58, 57
Arranging in ascending order = 41, 43, 57, 58, 61, 71, 92, 99, 127
Here n = 9 which is odd
Median = \(\frac { n+1 }{ 2 } \) th term = \(\frac { 9+1 }{ 2 } \) th term
= \(\frac { 10 }{ 2 } \) = 5th term = 61
By change 58 by 92, we get new order = 41, 43, 57, 61, 71, 92, 92, 99, 127
Median = 5th term = 71

Question 12.
The weights (in kg) of 15 students are : 31, 35, 27, 29, 32, 43, 37, 41, 34, 28, 36, 44, 45, 42, 30. Find the median. If the weight 44 kg is replaced by 46 kg and 27 kg by 25 kg, find the new median.
Solution:
Weights of 15 students are 31, 35, 27, 29, 32, 43, 37, 41, 34, 28, 36, 44, 45, 42, 30
Writing in ascending order = 27, 28, 29, 30, 31, 32, 34, 35, 36, 37, 41, 42, 43, 44, 45
here n = 15 which is odd
n+1 15+1
Median = \(\frac { n+1 }{ 2 } \) th term = \(\frac { 15+1 }{ 2 } \)
= \(\frac { 16 }{ 2 } \)th term = 8th term = 35 kg
By replacing 44 kg by 46 kg and 27 kg by 25 kg we get new order,
25, 28, 29, 30, 31, 32, 34, 35, 36, 37, 41, 42, 43, 45, 46
Median = 8th term = 35 kg

Question 13.
The following observations have been arranged in ascending order. If the median of the data is 63, find the value of x: 29, 32, 48, 50, x, x + 2, 72, 78, 84, 95
Solution:
Median = 63
29, 32, 48, 50, x, x + 2, 72, 78, 84, 95
Here n = 10 which is even
median = \(\frac { 1 }{ 2 } \left[ \frac { n }{ 2 } th\quad term+\left( \frac { n }{ 2 } +1 \right) th\quad term \right] \)
= \(\frac { 1 }{ 2 } \left[ \frac { 10 }{ 2 } th\quad term+\left( \frac { 10 }{ 2 } +1 \right) th\quad term \right] \)
= \(\frac { 1 }{ 2 } \) [5th term + 6th term]
= \(\frac { 16 }{ 2 } \) [x+x+2] = \(\frac { 2x + 2 }{ 2 } \) = x + 1
x + 1 = 63 = x = 63 – 1 = 62
Hence x = 62

Hope given RD Sharma Class 9 Solutions Chapter 24 Measures of Central Tendency Ex 24.3 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 9 Solutions Chapter 24 Measures of Central Tendency Ex 24.2

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 24 Measures of Central Tendency Ex 24.2

Other Exercises

• RD Sharma Class 9 Solutions Chapter 24 Measures of Central Tendency Ex 24.1
• RD Sharma Class 9 Solutions Chapter 24 Measures of Central Tendency Ex 24.2
• RD Sharma Class 9 Solutions Chapter 24 Measures of Central Tendency Ex 24.3
• RD Sharma Class 9 Solutions Chapter 24 Measures of Central Tendency Ex 24.4
• RD Sharma Class 9 Solutions Chapter 24 Measures of Central Tendency VSAQS
• RD Sharma Class 9 Solutions Chapter 24 Measures of Central Tendency MCQS

Question 1.
Calculate the mean for the following distribution
x 5 6 7 8 9
f 4 8 14 11 3
Solution:

Question 2.
Find the mean of the following data:
x 19 21 23 25 27 29 31
f 13 15 16 18 16 15 13
Solution:

Question 3.
Find the mean of the following distribution:
x 10 12 20 25 35
f 3 10 15 7 5
Solution:

Question 4.
Five coins were simultaneously tossed 1000 times and at each toss the number of heads were observed. The number of tosses during which 0, 1, 2, 3, 4 and 5 heads were obtained are shown in the table below. Find the mean number of heads per toss.

Solution:

Question 5.
The mean of the following data is 20.6. Find the value of p.
x 10 15 p 25 35
f 3 10 25 7 5
Solution:
Mean = 20.6

Question 6.
If the mean of the following data is 15, find p?.
x 5 10 15 20 25
f 6 p 6 10 5
Solution:
Mean = 15

Question 7.
Find the value of p for the following distribution whose mean is 16.6.
x 8 12 15 p 20 25 30
f 12 16 20 24 16 8 4
Solution:
Mean = 16.6

Question 8.
Find the missing value of p for the following distribution whose mean is 12.58.
x 5 8 10 12 p 20 25
f 2 5 8 22 7 4 2
Solution:
Mean = 12.58

Question 9.
Find the missing frequency (p) for the following distribution whose mean is 7.68.
x 3 5 7 9 11 13
f 6 8 15 p 8 4
Solution:
Mean = 7.68

Question 10.
Find the value of p, if the mean of the following distribution is 20.
x 15 17 19 20 + p 23
f    2  3   4     5p     6
Solution:
Mean = 20

Question 11.
Candidates of four schools appear in a mathematics test. The data were as follows:

If the average score of the candidates of all the four schools is 66, find the number of candidates that appeared from school III.
Solution:
Let number of candidates in school III = p
Then total number of candidates in 4 schools = 60 + 48 + p + 40 = 148 + p
Average score of 4 schools = 66
∴Total score = (148 + p) x 66
Now mean score of 60 in school I = 75 .
∴Total = 60 x 75 = 4500
In school II, mean of 48 = 80
∴Total = 48 x 80 = 3840
In school III, mean of p = 55
∴Total = 55 x p = 55p
and in school IV, mean of 40 = 50
∴Total = 40 x 50 = 2000
Now total of candidates of 4 schools = 148 + p
and total score = 4500 + 3840 + 55p + 2000 = 10340 + 55p
∴10340 + 55p = (148 + p) x 66 = 9768 + 66p
=> 10340 – 9768 = 66p – 55p
=> 572 = 11p
∴ p = \(\frac { 572 }{ 11 } \)
Number of candidates in school III = 52

Question 12.
Find the missing frequencies in the following frequency distribution if it is known that the mean of the distribution is 50.
x 10 30 50 70 90
f 17 f1 32 f1 19
Total 120
Solution:
Mean = 50

Hope given RD Sharma Class 9 Solutions Chapter 24 Measures of Central Tendency Ex 24.2 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.