RD Sharma Class 9 Solutions Chapter 11 Co-ordinate Geometry Ex 11.1
These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 11 Co-ordinate Geometry Ex 11.1
Other Exercises
- RD Sharma Class 9 Solutions Chapter 11 Co-ordinate Geometry Ex 11.1
- RD Sharma Class 9 Solutions Chapter 11 Co-ordinate Geometry Ex 11.2
- RD Sharma Class 9 Solutions Chapter 11 Co-ordinate Geometry VSAQS
- RD Sharma Class 9 Solutions Chapter 11 Co-ordinate Geometry MCQS
Question 1.
In a ∆ABC, if ∠A = 55°, ∠B = 40°, find ∠C.
Solution:
∵ Sum of three angles of a triangle is 180°
∴ In ∆ABC, ∠A = 55°, ∠B = 40°
But ∠A + ∠B + ∠C = 180° (Sum of angles of a triangle)
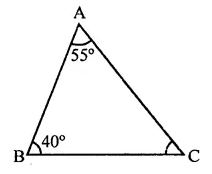
⇒ 55° + 40° + ∠C = 180°
⇒ 95° + ∠C = 180°
∴ ∠C= 180° -95° = 85°
Question 2.
If the angles of a triangle are in the ratio 1:2:3, determine three angles.
Solution:
Ratio in three angles of a triangle =1:2:3
Let first angle = x
Then second angle = 2x
and third angle = 3x
∴ x + 2x + 3x = 180° (Sum of angles of a triangle)
⇒6x = 180°
⇒x = \(\frac { { 180 }^{ \circ } }{ 6 }\) = 30°
∴ First angle = x = 30°
Second angle = 2x = 2 x 30° = 60°
and third angle = 3x = 3 x 30° = 90°
∴ Angles are 30°, 60°, 90°
Question 3.
The angles of a triangle are (x – 40)°, (x – 20)° and (\(\frac { 1 }{ 2 }\) x – 10)°. Find the value of x.
Solution:
∵ Sum of three angles of a triangle = 180°
∴ (x – 40)° + (x – 20)° + (\(\frac { 1 }{ 2 }\)x-10)0 = 180°
⇒ x – 40° + x – 20° + \(\frac { 1 }{ 2 }\)x – 10° = 180°
⇒ x + x+ \(\frac { 1 }{ 2 }\)x – 70° = 180°
⇒ \(\frac { 5 }{ 2 }\)x = 180° + 70° = 250°
⇒ x = \(\frac { { 250 }^{ \circ }x 2 }{ 5 }\) = 100°
∴ x = 100°
Question 4.
Two angles of a triangle are equal and the third angle is greater than each of those angles by 30°. Determine all the angles of the triangle.
Solution:
Let each of the two equal angles = x
Then third angle = x + 30°
But sum of the three angles of a triangle is 180°
∴ x + x + x + 30° = 180°
⇒ 3x + 30° = 180°
⇒3x = 150° ⇒x = \(\frac { { 150 }^{ \circ } }{ 3 }\) = 50°
∴ Each equal angle = 50°
and third angle = 50° + 30° = 80°
∴ Angles are 50°, 50° and 80°
Question 5.
If one angle of a triangle is equal to the sum of the other two, show that the triangle is a right triangle.
Solution:
In the triangle ABC,
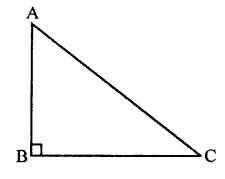
∠B = ∠A + ∠C
But ∠A + ∠B + ∠C = 180°
⇒∠B + ∠A + ∠C = 180°
⇒∠B + ∠B = 180°
⇒2∠B = 180°
∴ ∠B = \(\frac { { 180 }^{ \circ } }{ 2 }\) = 90°
∵ One angle of the triangle is 90°
∴ ∆ABC is a right triangle.
Question 6.
Can a triangle have:
(i) Two right angles?
(ii) Two obtuse angles?
(iii) Two acute angles?
(iv) All angles more than 60°?
(v) All angles less than 60°?
(vi) All angles equal to 60°?
Justify your answer in each case.
Solution:
(i) In a triangle, two right-angles cannot be possible. We know that sum of three angles is 180° and if there are two right-angles, then the third angle will be zero which is not possible.
(ii) In a triangle, two obtuse angle cannot be possible. We know that the sum of the three angles of a triangle is 180° and if there are
two obtuse angle, then the third angle will be negative which is not possible.
(iii) In a triangle, two acute angles are possible as sum of three angles of a trianlge is 180°.
(iv) All angles more than 60°, they are also not possible as the sum will be more than 180°.
(v) All angles less than 60°. They are also not possible as the sum will be less than 180°.
(vi) All angles equal to 60°. This is possible as the sum will be 60° x 3 = 180°.
Question 7.
The angles of a triangle are arranged in ascending order of magnitude. If the difference between two consecutive angle is 10°, find the three angles.
Solution:
Let three angles of a triangle be x°, (x + 10)°, (x + 20)°
But sum of three angles of a triangle is 180°
∴ x + (x+ 10)° + (x + 20) = 180°
⇒ x + x+10°+ x + 20 = 180°
⇒ 3x + 30° = 180°
⇒ 3x = 180° – 30° = 150°
∴ x = \(\frac { { 180 }^{ \circ } }{ 2 }\) = 50°
∴ Angle are 50°, 50 + 10, 50 + 20
i.e. 50°, 60°, 70°
Question 8.
ABC is a triangle is which ∠A = 72°, the internal bisectors of angles B and C meet in O. Find the magnitude of ∠BOC.
Solution:
In ∆ABC, ∠A = 12° and bisectors of ∠B and ∠C meet at O
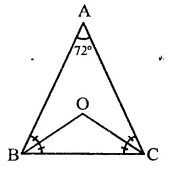
Now ∠B + ∠C = 180° – 12° = 108°
∵ OB and OC are the bisectors of ∠B and ∠C respectively
∴ ∠OBC + ∠OCB = \(\frac { 1 }{ 2 }\) (B + C)
= \(\frac { 1 }{ 2 }\) x 108° = 54°
But in ∆OBC,
∴ ∠OBC + ∠OCB + ∠BOC = 180°
⇒ 54° + ∠BOC = 180°
∠BOC = 180°-54°= 126°
OR
According to corollary,
∠BOC = 90°+ \(\frac { 1 }{ 2 }\) ∠A
= 90+ \(\frac { 1 }{ 2 }\) x 72° = 90° + 36° = 126°
Question 9.
The bisectors of base angles of a triangle cannot enclose a right angle in any case.
Solution:
In right ∆ABC, ∠A is the vertex angle and OB and OC are the bisectors of ∠B and ∠C respectively
To prove : ∠BOC cannot be a right angle
Proof: ∵ OB and OC are the bisectors of ∠B and ∠C respectively
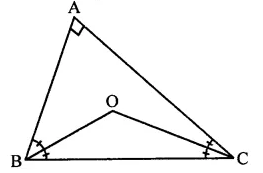
∴ ∠BOC = 90° x \(\frac { 1 }{ 2 }\) ∠A
Let ∠BOC = 90°, then
\(\frac { 1 }{ 2 }\) ∠A = O
⇒∠A = O
Which is not possible because the points A, B and C will be on the same line Hence, ∠BOC cannot be a right angle.
Question 10.
If the bisectors of the base angles of a triangle enclose an angle of 135°. Prove that the triangle is a right triangle.
Solution:
Given : In ∆ABC, OB and OC are the bisectors of ∠B and ∠C and ∠BOC = 135°
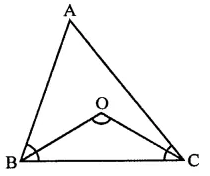
To prove : ∆ABC is a right angled triangle
Proof: ∵ Bisectors of base angles ∠B and ∠C of the ∆ABC meet at O
∴ ∠BOC = 90°+ \(\frac { 1 }{ 2 }\)∠A
But ∠BOC =135°
∴ 90°+ \(\frac { 1 }{ 2 }\) ∠A = 135°
⇒ \(\frac { 1 }{ 2 }\)∠A= 135° -90° = 45°
∴ ∠A = 45° x 2 = 90°
∴ ∆ABC is a right angled triangle
Question 11.
In a ∆ABC, ∠ABC = ∠ACB and the bisectors of ∠ABC and ∠ACB intersect at O such that ∠BOC = 120°. Show that ∠A = ∠B = ∠C = 60°.
Solution:
Given : In ∠ABC, BO and CO are the bisectors of ∠B and ∠C respectively and ∠BOC = 120° and ∠ABC = ∠ACB
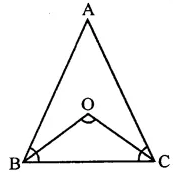
To prove : ∠A = ∠B = ∠C = 60°
Proof : ∵ BO and CO are the bisectors of ∠B and ∠C
∴ ∠BOC = 90° + \(\frac { 1 }{ 2 }\)∠A
But ∠BOC = 120°
∴ 90°+ \(\frac { 1 }{ 2 }\) ∠A = 120°
∴ \(\frac { 1 }{ 2 }\) ∠A = 120° – 90° = 30°
∴ ∠A = 60°
∵ ∠A + ∠B + ∠C = 180° (Angles of a triangle)
∠B + ∠C = 180° – 60° = 120° and ∠B = ∠C
∵ ∠B = ∠C = \(\frac { { 120 }^{ \circ } }{ 2 }\) = 60°
Hence ∠A = ∠B = ∠C = 60°
Question 12.
If each angle of a triangle is less than the sum of the other two, show that the triangle is acute angled.
Solution:
In a ∆ABC,
Let ∠A < ∠B + ∠C
⇒∠A + ∠A < ∠A + ∠B + ∠C
⇒ 2∠A < 180°
⇒ ∠A < 90° (∵ Sum of angles of a triangle is 180°)
Similarly, we can prove that
∠B < 90° and ∠C < 90°
∴ Each angle of the triangle are acute angle.
Hope given RD Sharma Class 9 Solutions Chapter 11 Co-ordinate Geometry Ex 11.1 are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.