RD Sharma Class 9 Solutions Chapter 24 Measures of Central Tendency Ex 24.2
These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 24 Measures of Central Tendency Ex 24.2
Other Exercises
- RD Sharma Class 9 Solutions Chapter 24 Measures of Central Tendency Ex 24.1
- RD Sharma Class 9 Solutions Chapter 24 Measures of Central Tendency Ex 24.2
- RD Sharma Class 9 Solutions Chapter 24 Measures of Central Tendency Ex 24.3
- RD Sharma Class 9 Solutions Chapter 24 Measures of Central Tendency Ex 24.4
- RD Sharma Class 9 Solutions Chapter 24 Measures of Central Tendency VSAQS
- RD Sharma Class 9 Solutions Chapter 24 Measures of Central Tendency MCQS
Question 1.
Calculate the mean for the following distribution
x 5 6 7 8 9
f 4 8 14 11 3
Solution:
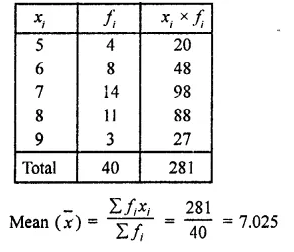
Question 2.
Find the mean of the following data:
x 19 21 23 25 27 29 31
f 13 15 16 18 16 15 13
Solution:
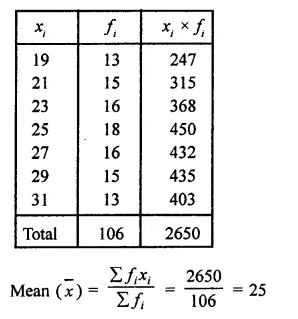
Question 3.
Find the mean of the following distribution:
x 10 12 20 25 35
f 3 10 15 7 5
Solution:
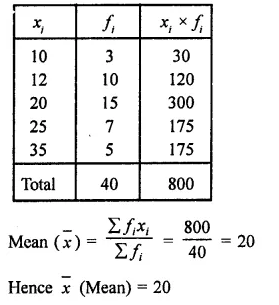
Question 4.
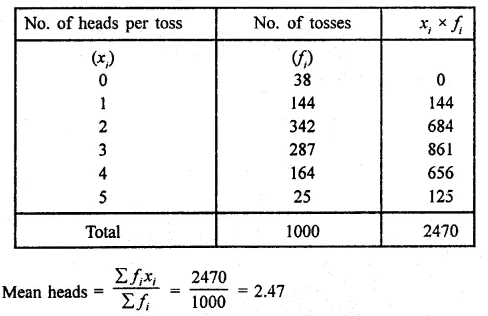
Five coins were simultaneously tossed 1000 times and at each toss the number of heads were observed. The number of tosses during which 0, 1, 2, 3, 4 and 5 heads were obtained are shown in the table below. Find the mean number of heads per toss.
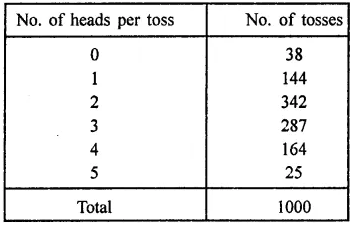
Solution:
Question 5.
The mean of the following data is 20.6. Find the value of p.
x 10 15 p 25 35
f 3 10 25 7 5
Solution:
Mean = 20.6

Question 6.
If the mean of the following data is 15, find p?.
x 5 10 15 20 25
f 6 p 6 10 5
Solution:
Mean = 15

Question 7.
Find the value of p for the following distribution whose mean is 16.6.
x 8 12 15 p 20 25 30
f 12 16 20 24 16 8 4
Solution:
Mean = 16.6

Question 8.
Find the missing value of p for the following distribution whose mean is 12.58.
x 5 8 10 12 p 20 25
f 2 5 8 22 7 4 2
Solution:
Mean = 12.58

Question 9.
Find the missing frequency (p) for the following distribution whose mean is 7.68.
x 3 5 7 9 11 13
f 6 8 15 p 8 4
Solution:
Mean = 7.68

Question 10.
Find the value of p, if the mean of the following distribution is 20.
x 15 17 19 20 + p 23
f 2 3 4 5p 6
Solution:
Mean = 20
Question 11.
Candidates of four schools appear in a mathematics test. The data were as follows:
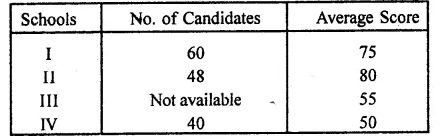
If the average score of the candidates of all the four schools is 66, find the number of candidates that appeared from school III.
Solution:
Let number of candidates in school III = p
Then total number of candidates in 4 schools = 60 + 48 + p + 40 = 148 + p
Average score of 4 schools = 66
∴Total score = (148 + p) x 66
Now mean score of 60 in school I = 75 .
∴Total = 60 x 75 = 4500
In school II, mean of 48 = 80
∴Total = 48 x 80 = 3840
In school III, mean of p = 55
∴Total = 55 x p = 55p
and in school IV, mean of 40 = 50
∴Total = 40 x 50 = 2000
Now total of candidates of 4 schools = 148 + p
and total score = 4500 + 3840 + 55p + 2000 = 10340 + 55p
∴10340 + 55p = (148 + p) x 66 = 9768 + 66p
=> 10340 – 9768 = 66p – 55p
=> 572 = 11p
∴ p = \(\frac { 572 }{ 11 } \)
Number of candidates in school III = 52
Question 12.
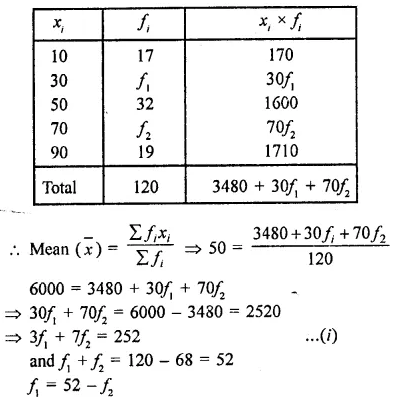
Find the missing frequencies in the following frequency distribution if it is known that the mean of the distribution is 50.
x 10 30 50 70 90
f 17 f1 32 f1 19
Total 120
Solution:
Mean = 50
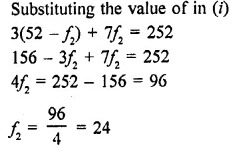
Hope given RD Sharma Class 9 Solutions Chapter 24 Measures of Central Tendency Ex 24.2 are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.