RS Aggarwal Class 9 Solutions Chapter 4 Lines and Triangles Ex 4A
These Solutions are part of RS Aggarwal Solutions Class 9. Here we have given RS Aggarwal Solutions Class 9 Chapter 4 Lines and Triangles Ex 4A.
Other Exercises
RS Aggarwal Solutions Class 9 Chapter 4 Lines and Triangles Ex 4A
RS Aggarwal Solutions Class 9 Chapter 4 Lines and Triangles Ex 4B
RS Aggarwal Solutions Class 9 Chapter 4 Lines and Triangles Ex 4C
RS Aggarwal Solutions Class 9 Chapter 4 Lines and Triangles Ex 4D
Question 1.
Solution:
(i)Angle : When two rays OA and OB meet at a point o, then ∠AOB is called an angle.
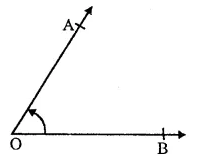
(ii) Interior of angle : The interior an angle is a set of all points in its plane which lie on the same side of OA as B and also on the same side of OB as A.
(iii) Obtuse angle : An angle greater than 90° but less than 180° is called an obtuse angle.
(iv) Reflex angle : An angle more than 180° but less than 360° is called a reflex angle.
(v) Complementary angles : Two angles are said to be complementary angles if their sum is 90°.
(vi) Supplementary angles : Two angles are said to be supplementary angles if their sum is 180°.
Question 2.
Solution:
∠A = 36°27’46”
∠B = 28° 43’39”
Adding, ∠A + ∠B = 64° 70′ 85″
We know that 60″ = 1′ and 60′ = 1°
∠A+ ∠B = 65° 11′ 25″ Ans.
Question 3.
Solution:
36° – 24° 28′ 30″
= 35° 59’60” – 25° 28’30”
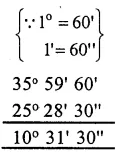
= 10° 31′ 30″ Ans.
Question 4.
Solution:
We know that two angles are complementary of their sum is 90°. Each of these two angles is complement to the other, therefore.
(i) Complement of 58° = 90° – 58° = 32°
(ii) Complement of 16° = 90° – 16° = 74°
(iii) Complement of \(\frac { 2 }{ 3 } \) of a right angle i.e.
of \(\frac { 2 }{ 3 } \) x 90° or 60° = 90° – 60° = 30°
= \(\frac { 2 }{ 3 } \) of right angle,
(iv) Complement of 46° 30′
= 90° – 46° 30′
= 43° 30′
(v) Complement of 52° 43′ 20°= 90° – 52° 43′ 20″
= 37° 16′ 40″
(vi) Complement of 68° 35′ 45″
= 90° – 68° 35′ 45″
= 21° 24′ 15″ Ans.
Question 5.
Solution:
We know that two angles are said to be supplement to each other of their sum is 180° therefore
(i) Supplement of 68° = 180° – 68° =112°
(ii) Supplement of 138° = 180° – 138° = 42°
(iii) Supplement of \(\frac { 3 }{ 5 } \) of a right angle or \(\frac { 3 }{ 5 } \) x 90° or 54°
= 180° – 54° = 126°
(iv) Supplement of 75° 36′ = 180° – 75° 36′ = 104° 24′
(v) Supplement of 124° 20′ 40″
= 180° – 124° 20′ 40″
= 55° 39′ 20″
(vi) Supplement of 108° 48′ 32″ = 180° – 108″ 48′ 32″ = 71° 11′ 28″ Ans.
Question 6.
Solution:
(i) Let the measure of required angle = x ,
their its complement = 90° – x
According to the condition,
x = 90° – x => 2x = 90°
=>x = \(\frac { { 90 }^{ o } }{ 2 } \) = 45°
Required angle = 45°
(ii) Let the measure of required angle = x then its supplement = 180° – x
According to the condition,
x = 180° – x => 2x = 180° = 90°
=>x = \(\frac {{ 180 }^{ o }}{ 2 }\) = 90°
Hence required angle = 90° Ans.
Question 7.
Solution:
Let required angle = x
then its complement = 90° – x
According to the condition,
x – (90° – x) = 36°
=> x – 90° + x = 36°
=> 2x = 36° + 90° = 126°
= \(\frac { { 126 }^{ o } }{ 2 } \) = 63°
Required angle = 63° Ans.
Question 8.
Solution:
Let the required angle = x
then its supplement = 180° – x
According to the condition,
(180° – x) – x = 25°
=> 180° – x – x = 25°
=> – 2x = 25° – 180°
=> – 2x = – 155°
=> x = \(\frac { { – 155 }^{ o } }{ – 2 } \)
= 77.5°
Hence required angle = 77.5° Ans.
Question 9.
Solution:
Let required angle = x
Then its complement = 90° – x
According to the condition,
x = 4 (90° – x) => x = 360° – 4x
=> x + 4x = 360° => 5x = 360°
x = \(\frac { { 360 }^{ o } }{ 5 } \) = 72°
Required angle = 72° Ans.
Question 10.
Solution:
Let required angle = x
Then its supplement = 180° – x
According to the condition,
x = 5 (180° – x)
=> x = 900° – 5x
=> x + 5x = 900°
=> 6x = 900°
=> x = \(\frac { { 900 }^{ o } }{ 6 } \) = 150°
Hence, required angle = 150° Ans
Question 11.
Solution:
Let required angle = x
then its supplement = 180° – x
and complement = 90° – x
According to the condition,
180° – x = 4 (90°- x)
=> 180° – x = 360° – 4x
=> – x + 4x — 360° – 180°
=> 3x= 180°
=> x = \(\frac { { 180 }^{ o } }{ 3 } \) = 60°
Required angle = 60° Ans.
Question 12.
Solution:
Let required angle = x
Then, its complement = 90° – x
and its supplement = 180° – x
According to the condition,
90° – x = \(\frac { 1 }{ 3 } \) (180° – x)
=> 90° – x = 60° – \(\frac { 1 }{ 3 } \) x
=> 90° – 60° = x – \(\frac { 1 }{ 3 } \) x
=> \(\frac { 2 }{ 3 } \) x = 30° =>x = \(\frac { { 30 }^{ o }X3\quad \quad }{ 2 } \) => x = 45° Ans.
Question 13.
Solution:
Let one angle = x
Then, its supplement = 180° – x
According to the condition,
x : (180° – x) = 3:2
=> \(\frac { x }{ { 180 }^{ o }-x } =\frac { 3 }{ 2 } \)
=>2x = 3(180°- x)
=> 2x = 540° – 3x
=> 2x + 3x = 540°
=> 5x = 540° => x = \(\frac { { 540 }^{ o } }{ 5 } \) = 108°
Angle = 108° and its supplement = 180° – 108° = 72°
Hence, angles are 108° and 72° Ans.
Question 14.
Solution:
Let angle = x
Then, its complementary angle = 90° – x
According to the condition,
x : (90° – x) = 4 : 5
=> \(\frac { x }{ { 90 }^{ o }-x } =\frac { 4 }{ 5 } \)
=> 5x = 4 (90° – x)
=> 5x = 360° – 4x
=> 5x + 4x = 360°
=> 9x = 360°
=> x = \(\frac { { 360 }^{ o } }{ 9 } ={ 40 }^{ o } \)
and its complement = 90° – 40° = 50°
Hence, angles are 40° and 50° Ans.
Question 15.
Solution:
Let the required angle = x
.’. its complement = 90° – x
and supplement = 180° – x
According to the condition,
7(90° – x) = 3(180° – x) – 10°
=> 630° – 7x = 3 (180° – x) – 10°
=> 630° – 7x = 540° – 3x – 10°
=> – 7x + 3x = 540° – 10° – 630°
– 4x = – 100°
x = \(\frac { { -100 }^{ o } }{ -4 } ={ 25 }^{ o }\)
Hence required angle = 25° Ans.
Hope given RS Aggarwal Solutions Class 9 Chapter 4 Lines and Triangles Ex 4A are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.