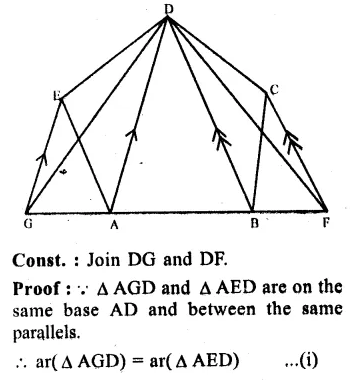
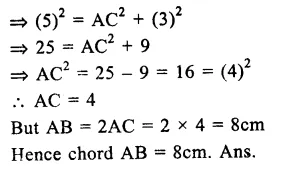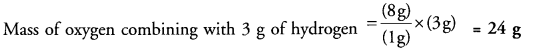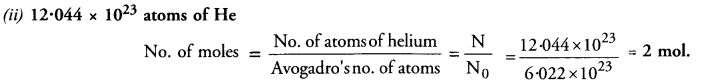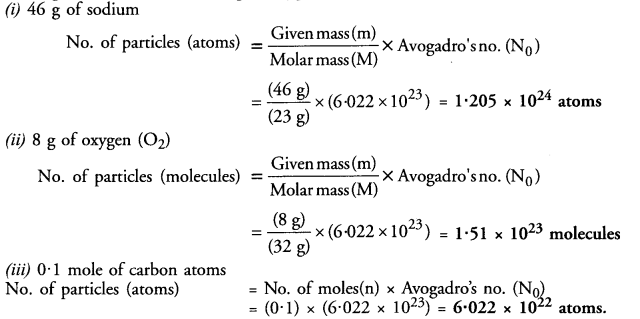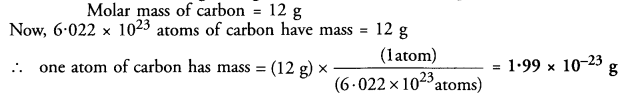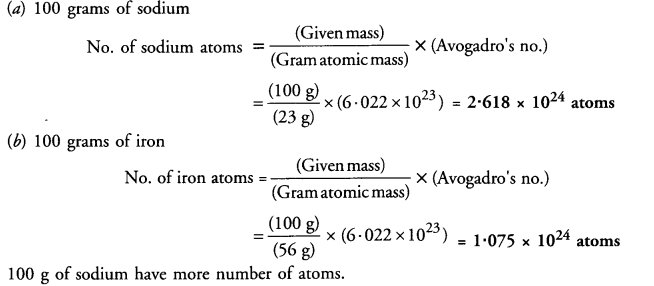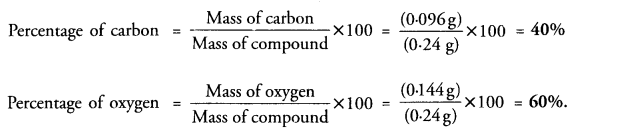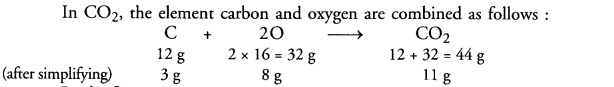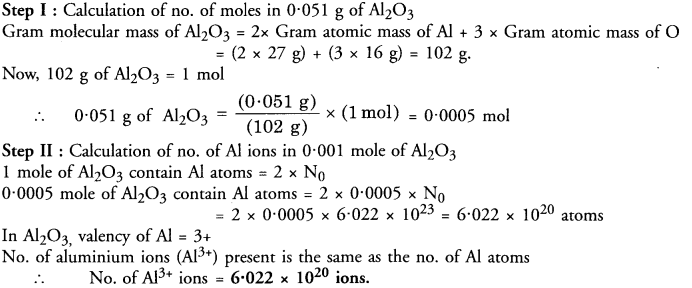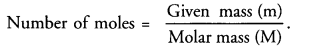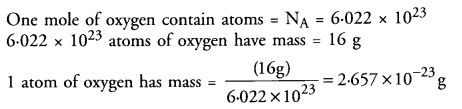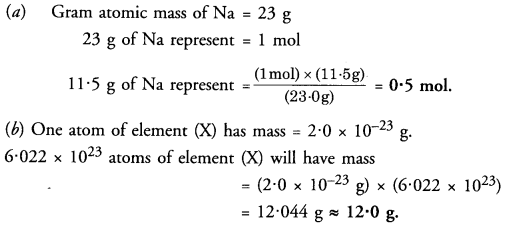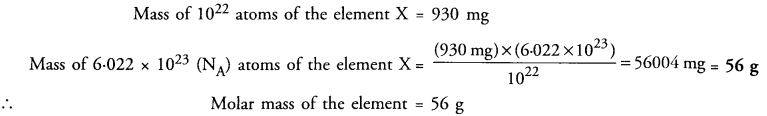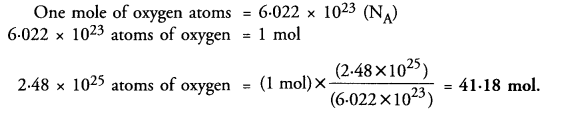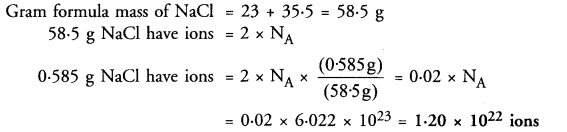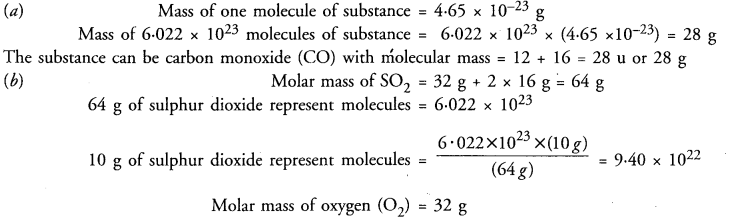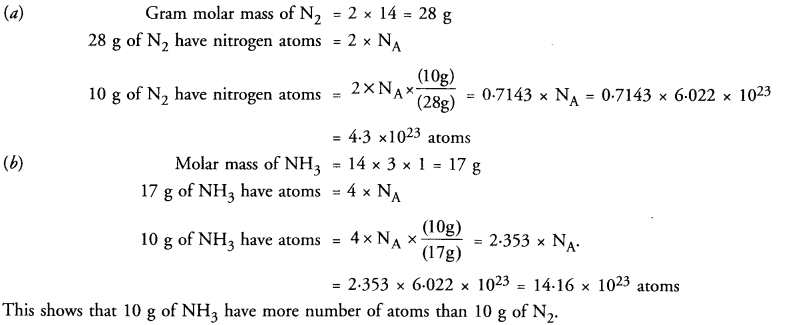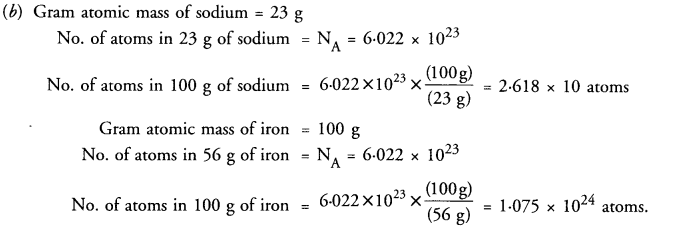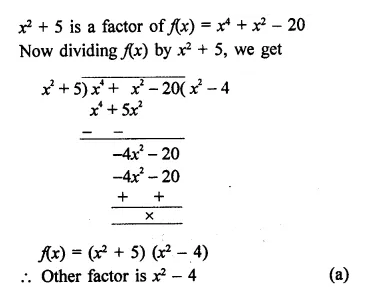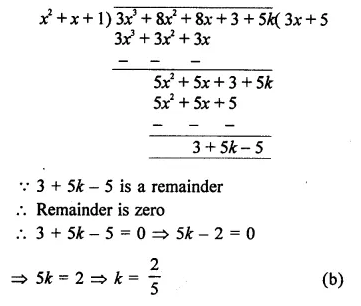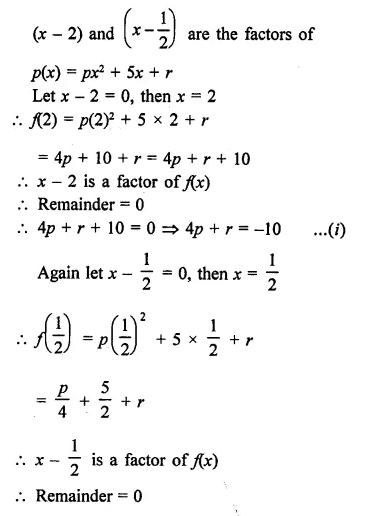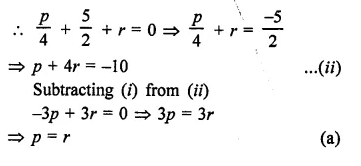CBSE Class 9 – Page 123

RS Aggarwal Class 9 Solutions Chapter 11 Circle Ex 11A

January 5, 2022June 21, 2018 by Prasanna

RS Aggarwal Class 9 Solutions Chapter 11 Circle Ex 11A

These Solutions are part of RS Aggarwal Solutions Class 9. Here we have given RS Aggarwal Solutions Class 9 Chapter 11 Circle Ex 11A.

Other Exercises

Question 1.
Solution:
Let AB be a chord of a circle with centre O. OC⊥AB and OA be the radius of the circle, then
AB = 16cm, OA = 10cm .
RS Aggarwal Class 9 Solutions Chapter 11 Circle Ex 11A Q1.1
OC ⊥ AB.
OC bisects AB at C
AC = \(\frac { 1 }{ 2 } \) AB = \(\frac { 1 }{ 2 } \) x 16 = 8cm

Question 2.
Solution:
Let AB be the chord of the circle with centre O and OC ⊥ AB, OA be the radius of the circle,
then OC = 3cm, OA = 5cm
RS Aggarwal Class 9 Solutions Chapter 11 Circle Ex 11A Q2.1
Now in right ∆ OAC,
OA² = AC² = OC² (Pythagoras Theorem)

Question 3.
Solution:
Let AB be the chord, OA be the radius of
the circle OC ⊥ AB
then AB = 30 cm, OC = 8cm
RS Aggarwal Class 9 Solutions Chapter 11 Circle Ex 11A Q3.1

Question 4.
Solution:
AB and CD are parallel chords of a circle with centre O.
RS Aggarwal Class 9 Solutions Chapter 11 Circle Ex 11A Q4.1

Question 5.
Solution:
Let AB and CD be two chords of a circle with centre O.
OA and OC are the radii of the circle. OL⊥AB and OM⊥CD.
RS Aggarwal Class 9 Solutions Chapter 11 Circle Ex 11A Q5.1

Question 6.
Solution:
In the figure, a circle with centre O, CD is its diameter AB is a chord such that CD⊥AB.
AB = 12cm, CE = 3cm.
Join OA.
∵ COD⊥AB which intersects AB at E
RS Aggarwal Class 9 Solutions Chapter 11 Circle Ex 11A Q6.1

Question 7.
Solution:
A circle with centre O, AB is diameter which bisects chord CD at E
i.e. CE = ED = 8cm and EB = 4cm
Join OC.
Let radius of the circle = r
RS Aggarwal Class 9 Solutions Chapter 11 Circle Ex 11A Q7.1

Question 8.
Solution:
Given : O is the centre of a circle AB is a chord and BOC is the diameter. OD⊥AB
To prove : AC || OD and AC = 20D
Proof : OD⊥AB
∵ D is midpoint of AB
RS Aggarwal Class 9 Solutions Chapter 11 Circle Ex 11A Q8.1

Question 9.
Solution:
Given : O is the centre of the circle two
chords AB and CD intersect each other at P inside the circle. PO bisects ∠BPD.
To prove : AB = CD.
RS Aggarwal Class 9 Solutions Chapter 11 Circle Ex 11A Q9.1

Question 10.
Solution:
Given : PQ is the diameter of the circle with centre O which is perpendicular to one chord AB and chord AB || CD.
PQ intersects AB and CD at E and F respectively
To prove : PQ⊥CD and PQ bisects CD.
RS Aggarwal Class 9 Solutions Chapter 11 Circle Ex 11A Q10.1

Question 11.
Solution:
Two circles with centre O and O’ intersect each other.
RS Aggarwal Class 9 Solutions Chapter 11 Circle Ex 11A Q11.1
To prove : The two circles cannot intersect each other at more than two points.
Proof : Let if opposite, the two circles intersect each other at three points P, Q and R.
Then these three points are non-collinear. But, we know that through three non- collinear points, one and only one circle can be drawn.
∵ Our supposition is wrong
Hence two circle can not intersect each other at not more than two points.
Hence proved

Question 12.
Solution:
Given : Two circles with centres O and O’ intersect each other at A and B. AB is a common chord. OO’ is joined.
AO and AO is joined.
RS Aggarwal Class 9 Solutions Chapter 11 Circle Ex 11A Q12.1

Question 13.
Solution:
Given : Two equal circles intersect each other at P and Q.
A straight line drawn through
P, is drawn which meets the circles at A and B respectively
To prove : QA = QB
RS Aggarwal Class 9 Solutions Chapter 11 Circle Ex 11A Q13.1

Question 14.
Solution:
Given : A circle with centre 0. AB and CD are two chords and diameter PQ bisects AB and CD at L and M
To Prove : AB || CD.
RS Aggarwal Class 9 Solutions Chapter 11 Circle Ex 11A Q14.1

Question 15.
Solution:
Given : Two circles with centres A and B touch each other at C internally. A, B arc joined. PQ is the perpendicular bisector of AB intersecting it at L and meeting the bigger circle at P and Q respectively and radii of the circles are 5cm and 3cm. i.e. AC = 5cm,BC = 3cm
Required : To find the lenght of PQ
RS Aggarwal Class 9 Solutions Chapter 11 Circle Ex 11A Q15.1

Question 16.
Solution:
Given : AB is a chord of a circle with centre O. AB is produced to C such that BC = OB, CO is joined and produced to meet the circle at D.
∠ ACD = y°, ∠ AOD = x°
To prove : x = 3y
RS Aggarwal Class 9 Solutions Chapter 11 Circle Ex 11A Q16.1

Question 17.
Solution:
Given : O is the centre of a circle AB and AC are two chords such that AB = AC
OP⊥AB and OQ⊥AC.
which intersect AB and AC at M and N
respectively. PB and QC are joined.
To prove : PB = QC.
RS Aggarwal Class 9 Solutions Chapter 11 Circle Ex 11A Q17.1

Question 18.
Solution:
Given : In a circle with centre O, BC is its diameter. AB and CD are two chords such that AB || CD.
To prove : AB = CD
Const. Draw OL⊥AB
OM⊥CD.
Proof : In ∆ OLB and ∆ OCM,
OB = OC (radii of the same circle)
∠ OLB = ∠ OMC (each 90°)
∠ OBL = ∠ OCM (alternate angles)
RS Aggarwal Class 9 Solutions Chapter 11 Circle Ex 11A Q18.1

Question 19.
Solution:
Equilateral ∆ ABC in inscribed in a circle in which
AB = BC = CA = 9cm.
RS Aggarwal Class 9 Solutions Chapter 11 Circle Ex 11A Q19.1

Question 20.
RS Aggarwal Class 9 Solutions Chapter 11 Circle Ex 11A Q20.1
Solution:
Given : AB and AC are two equal chords of a circle with centre O
To Prove : O lies on the bisector of ∠ BAC

Question 21.
Solution:
Given : OPQR is a square with centre O, a circle is drawn which intersects the square at X and Y.
To Prove : Q = QY
Const. Join OX and OY
RS Aggarwal Class 9 Solutions Chapter 11 Circle Ex 11A Q21.1

Hope given RS Aggarwal Solutions Class 9 Chapter 11 Circle Ex 11A are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

NCERT Solutions For Class 9 Science Chapter 3 Atoms and Molecules

January 5, 2022June 21, 2018 by Prasanna

NCERT Solutions For Class 9 Science Chapter 3 Atoms and Molecules

These Solutions are part of NCERT Solutions for Class 9 Science. Here we have given NCERT Solutions for Class 9 Science Chapter 3 Atoms and Molecules. LearnInsta.com provides you the Free PDF download of NCERT Solutions for Class 9 Science (Chemistry) Chapter 3 – Atoms and Molecules solved by Expert Teachers as per NCERT (CBSE) Book guidelines. All Chapter 3 – Atoms and Molecules Exercise Questions with Solutions to help you to revise complete Syllabus and Score More marks.

More Resources

NCERT IN TEXT PROBLEMS

IN TEXT QUESTIONS

Question 1.
In a reaction, 5.3 g of sodium carbonate reacted with 6.0 g of ethanoic acid. The products were 2.2 g of carbon dioxide, 0.9 g of water and 8.2 g of sodium ethanoate. Show that these observations are in agreement with the law of conservation of mass. (CBSE 2012)
Answer:
The chemical reaction leading to products is :
sodium carbonate + ethanoic acid ———–> sodium ethanoate + carbon dioxide + water.
Mass of reactants = (5.3 + 6.0) = 1.3 g
Mass of products = (8.2 + 2.2 + 0.9) = 11.3 g.
The reactants and products have same mass. This means that there was no loss of mass during the reaction. Therefore, the data is in agreement with law of conservation of mass.

Question 2.
Hydrogen and oxygen combine in the ratio of 1 : 8 by mass to form water. What mass of oxygen gas would be required to react with 3 g of hydrogen gas ?
Answer:
According to available data,
Mass of oxygen combining with 1 g of hydrogen = 8 g.
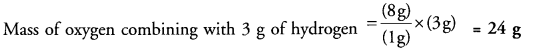
NCERT Solutions For Class 9 Science Chapter 3 Atoms and Molecules 1
Question 3:
Which postulate of Dalton’s Atomic theory is the basis of law of conservation of mass ? (CBSE 2012)
Answer:
The law of conservation mass is based on the following postulate of Dalton’s Atomic theory.
“Atoms can neither be created nor destroyed during a physical change or a chemical reaction.”

Question 4.
Which postulate of Dalton’s Atomic theory can explain the law of definite proportions ?
Answer:
The law of definite proportions is based on the following postulate of Dalton’s Atomic theory.
“All atoms of a particular element are identical in every respect. This means that they have same mass, same size and also same chemical properties.”

Question 5.
Define atomic mass unit.
Answer:
Atomic mass unit may be defined as :
The mass of one-twelfth (1/12) of the mass of one atom of carbon taken as 12 u. It is represented as 1 u (unified mass).

Question 6.
Why is not possible to see an atom with naked eye ?
Answer:
It is not possible to see an atom with naked eye because of its extremely small size. For example, the radius of an atom of hydrogen is of the order of 10^-10 m. Actually an atom is regarded as a microscopic particle. These microscopic particles cannot be seen with naked eye.

Question 7.
Write down the formulae of :
(i) sodium oxide
(ii) aluminium chloride
(iii) sodium sulphide
(iv) magnesium hydroxide.
Answer:
NCERT Solutions For Class 9 Science Chapter 3 Atoms and Molecules 2
Question 8.
Write the names of the compounds represented by the following formulae :
(i) Al₂(SO₄)₃
(ii) CaCl₂
(Hi) K₂SO₄
(iv) KNO₃
(v) CaCO₃.
Answer:
(i) Aluminium sulphate
(ii) Calcium chloride
(iii) Potassium sulphate
(iv) Potassium nitrate
(v) Calcium carbonate

Question 9.
What is meant by the term chemical formula ?
Answer:
Molecule represents a group of two or more atoms (same or different) chemically bonded to each other and held tightly by strong attractive forces. Molecules are represented in terms of symbols of constituting atoms and it is known as chemical formula.

Question 10.
How many atoms are present in
(i) H₂S molecule
(ii) PO₄^3-ion ?
Answer:
(i) Three
(ii) Five.

Question 11.
Calculate the molecular masses of :
(i) H₂
(ii) O₂
(iii) Cl₂
(iv) CO₂
(v) CH₄
(vi) C₂H₆
(vii) C₂H₄
(viii) NH₃
(ix) CH₃OH.
Answer:
(i) Hydrogen (H₂)
Molecular mass of H₂ = 2 x Atomic mass of H = (2 x 1 u) = 2 u.
(ii) Oxygen (O₂)
Molecular mass of O₂ = 2 x Atomic mass of O = (2 x 16 u) = 32 u.
(iii) Chlorine (CI₂)
Molecular mass of Cl₂ = 2 x Atomic mass of Cl = (2 x 35’5 u) = 71 u.
(iv) Carbon dioxide (CO₂)
Molecular mass of CO₂ = (1 x Atomic mass of C) + (2 x Atomic mass of O)
= (1 x 12 u) + (2 x 16 u) = 12 u + 32 u = 44 u.
(v) Methane (CH₄)
Molecular mass of CH₄ = ( 1 x Atomic mass of C) + (4 x Atomic mass of H)
= ( 1 x 12 u) + (4 x 1 u) = 16 u.
(vi) Ethane (C₂H₆)
Molecular mass of C₂H₆ = (2 x Atomic mass of C) + (6 x Atomic mass of H)
= (2 x 12 u) + (6 x 1 u) = 30 u.
(vii) Ethylene (C₂H₄)
Molecular mass of C₂H₄ =(2 x Atomic mass of C) + (4 x Atomic mass of H)
= (2 x 12 u) + (4 x 1 u) = 28 u.
(viii) Ammonia (NH₃)
Molecular mass of NH₃ = (1 x Atomic mass ofN) + (3 x Atomic mass of H)
= (1 x 14 u) + ( 3 x 1 u) = 17 u.
(ix) Methyl alcohol (CH₃OH)
Molecular mass of CH₃OH = (1 x Atomic mass of C) + (4 x Atomic mass of H)
+ (1 x Atomic mass of O)
= (1 x 12 u) + (4 x 1 u) + (1 x 16 u) = 32 u.

Question 12.
Calculate the formula unit mass of :
(i) ZnO
(ii) Na₂O
(iii) K₂CO₃.
Given : Atomic masses of Zn = 65 u, Na = 23 u, K = 39 u, C = 12 u and O = 16 u.
Answer:
(i) Formula unit mass of ZnO (Zinc oxide)
= (1 x Atomic mass of Zn) +(1 x Atomic mass of O)
= (1 x 65 u) + (1 x 16 u) = 81 u.
(ii) Formula unit mass of Na₂O (Sodium oxide)
= (2 x Atomic mass of Na) + (1 x Atomic mass of O)
= (2 x 23 u) + (1 x 16 u) = 62 u.
(iii) Formula unit mass of K₂CO₃ (Potassium carbonate).
= (2 x Atomic mass of K) + (1 x Atomic mass of C) + (3 x Atomic mass of O)
= (2 x 39 u) + (1 x 12 u) + (3 x 16 u) = 138 u

Question 13.
Calculate the number of moles of the following :
(i) 52 g of He
(ii) 12.044 x 10²³ atoms of He.
Answer:
NCERT Solutions For Class 9 Science Chapter 3 Atoms and Molecules 3

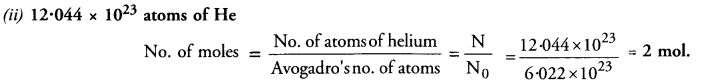
Question 14.
Calculate the number of particles in each of the following :
(i) 46 g of sodium atoms
(ii) 8 g of oxygen (O₂)
(iii) 0.1 mole of carbon atoms.
Answer:
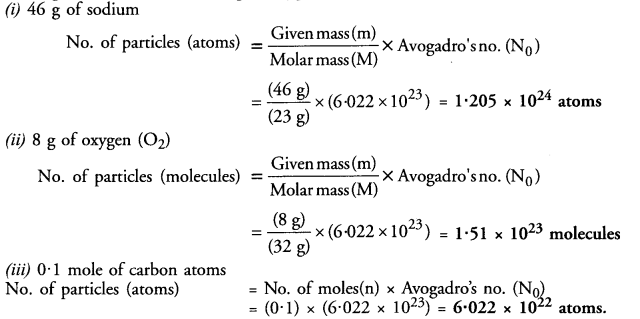
NCERT Solutions For Class 9 Science Chapter 3 Atoms and Molecules 5

Question 15.
If one mole of carbon weighs 12 grams, what is the mass (in gram) of one atom of carbon ?
Answer:
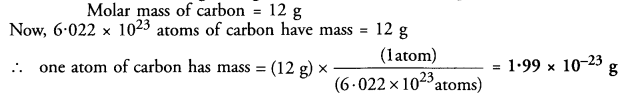
NCERT Solutions For Class 9 Science Chapter 3 Atoms and Molecules 6

Question 16.
Which has more number of atoms ?
(a) 100 grams of sodium
(b) 100 grams of iron
(Given : atomic mass of Na = 23 u ; Fe = 56 u)
Answer:
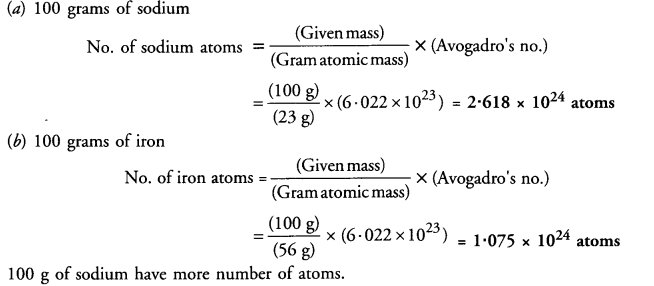
NCERT Solutions For Class 9 Science Chapter 3 Atoms and Molecules 7

NCERT END EXERCISE

Question 1.
0.24 g of sample of a compound of oxygen and boron was found by analysis to contain 0.096 g of boron
and 0.144 g of oxygen. Calculate the percentage composition of the compound by weight.
Answer:
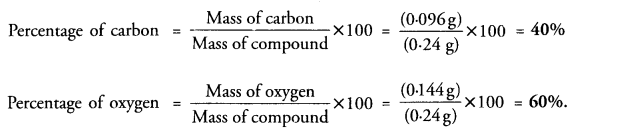
NCERT Solutions For Class 9 Science Chapter 3 Atoms and Molecules 8

Question 2.
When 3.0 g of carbon is burnt in 8.0 g of oxygen, 11.0 g of carbon dioxide is formed. What mass of carbon dioxide will be formed when 3.0 g of carbon is burnt in 50.0 g of oxygen ? Which law of chemical combination will govern your answer ? (CBSE 2011, 2012)
Answer:
Carbon and oxygen react to form carbon dioxide according to the equation Carbon (C) + Oxygen (O₂) > Carbon dioxide (CO₂)
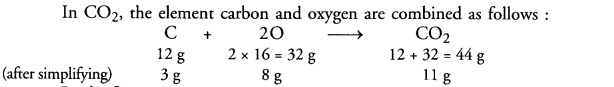
NCERT Solutions For Class 9 Science Chapter 3 Atoms and Molecules 9
In the first case :
3.0 g of carbon are burnt in 8.0 g of oxygen to form 11.0 g of CO₂ In the second case :
3.0 g of carbon must also combine with 8.0 g of oxygen only. This means that (50 – 8) = 42 g of oxygen will remain unreacted.
The mass of CO₂ in this case must be also 11 g.
The answer is based on Law of constant proportions.
In the second case, only 8.0 g of oxygen react although 50.0 g are available. This shows that the mass of carbon dioxide (11.0 g) formed depends upon the mass of carbon (3.0 g) or the substance present in smaller amount. In general, the substance (element or compound) present in smaller amount in a reaction limits the participation of the other reactants. It is quite often called limiting reactant. Carbon is the limiting reactant in this case. It limits the participation of oxygen and also the formation of carbon dioxide.

Question 3.
What are polyatomic ions ? Give examples. (CBSE 2015)
Answer:
Polyatomic ions are the group of atoms which carry either positive charge (cations) or negative charge (anions). For example,

Carbonate ion (CO₃)^2-
Nitrate ion (NO₃)^–
Ammonium ion (NH₄)⁺
Phosphate ion (PO₄)^3-.

Question 4.
Write the chemical formulae of the following :
Answer:
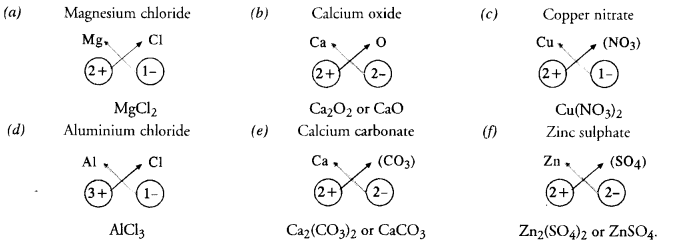
NCERT Solutions For Class 9 Science Chapter 3 Atoms and Molecules 10

Question 5.
Give the names of the elements present in the following compounds :
(a) Quick lime
(b) Hydrogen bromide
(c) Baking powder
(d) Potassium sulphate.
Answer:
The names of elements present can be given only if the chemical formula of the compound is known. For example,
(a) Quick lime : It is the commercial name of the compound. Its chemical name is calcium oxide and the
chemical formula is CaO.
Elements present : calcium (Ca) : oxygen (O).
(b) Hydrogen bromide : The chemical formula of the compound is HBr
Elements present : hydrogen (H) ; bromine (Br).
(c) Baking powder : It is the commercial name of the compound. Its chemical name is sodium hydrogen carbonate and the chemical formula is NaHCO₃
Elements present : sodium (Na), hydrogen (H), carbon (C), oxygen (O).
(d) Potassium sulphate : The chemical formula of the compound is K₂SO₄
Elements present : potassium (K), sulphur (S), oxygen (O).

Question 6.
Calculate the molar mass of the following substances :
(a) Ethyne, C₂H₂
(b) Sulphur molecule, S₈
(c) Phosphorus molecule, P₄ (Atomic mass of phosphorus = 31)
(d) Nitric acid, HNO₃
(e) Hydrochloric acid, HCl.
Answer:
(a) Ethyne, C₂H₂
Molar mass of C₂H₂ = (2 x Atomic mass of C) + (2 x Atomic mass of H)
= (2 x 12 u) + (2 x 1 u) = 26 u.
(b) Sulphur molecule, S₈
Molar mass of S₈ = 8 x Atomic mass of S = (8 x 32 u) = 256 u
(c) Phosphorus molecule, P₄
Molar mass of P₄ =4 x Atomic mass of P = (4 x 31 u) = 124 u
(d) Nitric acid, HNO₃
Molar mass of HNO₃ = (1 x Atomic mass of H) + (1 x Atomic mass of N) + ( 3 x Atomic mass of O)
= (1 x 1 u) + (1 x 14 u) + (3 x 16 u) = 63 u.
(e) Hydrochloric acid, HCl.
Molar mass of HCl = (1 x Atomic mass of H) + (1 x Atomic mass of Cl)
= (1 x 1 u) + (1 x 35.5 u) = 36.5 u.

Question 7.
What is the mass of :
(a) 1 mole of nitrogen atoms ?
(b) 4 moles of aluminium atoms (Atomic mass of aluminium = 27) ?
(c) 10 moles of sodium sulphite (Na₂SO₃) ?
Answer:
(a) 1 mole of nitrogen atoms
Mass of 1 mole of nitrogen (N) atoms = 14 u
(b) 4 moles of aluminium atoms
Mass of 1 mole of aluminium (Al) atoms = 27 u
Mass of 4 moles of aluminium (Al) atoms = 4 x 27 = 108 u
(c) 10 moles of sodium sulphite (Na₂SO₃)
Molar mass of Na₂SO₃ = 2 x Atomic mass of Na + Atomic mass of S + 3 x Atomic mass of O
= 2 x 23 + 32 + 3 x 16 = 126 u
1 mole of sodium sulphite has mass = 126 u
10 moles of sodium sulphite have mass = 10 x 126 = 1260 u.

Question 8.
Convert into moles
(a) 12 g of oxygen gas
(b) 20 g of water
(c) 22 g of carbon dioxide.
Answer:
NCERT Solutions For Class 9 Science Chapter 3 Atoms and Molecules 11

Question 9.
What is the mass of :
(a) 0.2 mole of oxygen atoms ?
(b) 0.5 mole of water molecules ?
Answer:
(a) 0.2 mole of oxygen atoms
Mass of 1 mole of oxygen (O) atoms = 16 u
Mass of 0.2 mole of oxygen (O) atoms = 0.2 x 16 = 3.2 u
(b) 0.5 mole of water molecules
Mass of 1 mole of water (H₂O) molecules = 2 x 1 + 16 = 18 u
Mass of 0.5 mole of water (H2O) molecules = 0.5 x 18 = 9 u.

Question 10.
Calculate the number of molecules of sulphur (Sg) present in 16 g of solid sulphur.
Answer:
NCERT Solutions For Class 9 Science Chapter 3 Atoms and Molecules 12

Question 11.
Calculate the number of aluminium ions in 0.051 g of aluminium oxide (Al₂O₃). (CBSE 2012)
Answer:
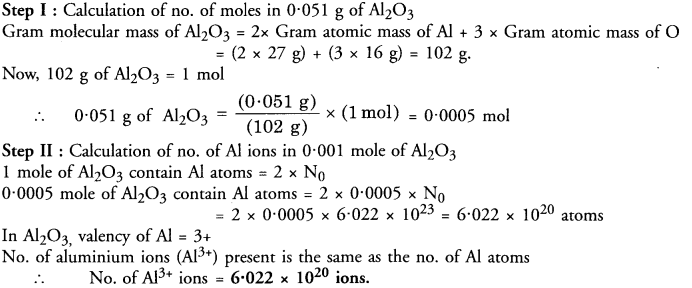
NCERT Solutions For Class 9 Science Chapter 3 Atoms and Molecules 13

VERY SHORT ANSWER QUESTIONS

Question 1.
Out of atoms and molecules, which can exist independently ?
Answer:
Molecules can exist independently. However, the atoms of noble gases (He, Ne, Ar, Kr, Xe) can also exist independently.

Question 2.
What does the symbol ‘u’ represent ?
Answer:
The symbol V represents unified mass.

Question 3.
Write the chemical symbols and Latin names of
(i) gold
(ii) mercury ?
Answer:
(i) Au (Aurum)
(ii) Hg (Hydrargyrum).

Question 4.
Are the mass of a molecule of a substance and its molar mass same ?
Answer:
No, they are different.

Question 5.
How are mass, molar mass and number of moles of a substance related to each other ?
Answer:
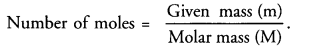
NCERT Solutions For Class 9 Science Chapter 3 Atoms and Molecules 14

Question 6.
Avogardo’s number represents how many particles ?
Answer:
Avogadro’s number (Ng) represents 6.022 x 10²³ particles.

Question 7.
Give an example of
(i) a divalent anion
(ii) a trivalent cation
(iii) a monovalent anion.
Answer:
(i) (SO₄)^2-
(ii) Al₃⁺
(iii) Cl^–

Question 8.
Calculate the molar mass of ethyl alcohol (C₂H₅OH).
Answer:
Molar mass of C₂H₅OH= (2 x gram atomic mass of C) + (6 x gram atomic mass of H)
+ (1 x Atomic mass of O)
= (2 x 12 g) + (6 x 1 g) + (1 x 16 g) = 46 g.

Question 9.
If one mole of oxygen atoms weigh 16 grams, calculate the mass of one atom of oxygen (in grams).
(CBSE 2014)
Answer:
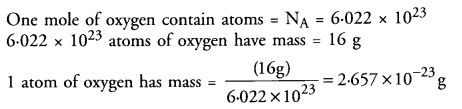
NCERT Solutions For Class 9 Science Chapter 3 Atoms and Molecules 15

Question 10.
What is the valency of calcium in CaCO₃ ?
Answer:
The valency of Ca in CaCO₃ is 2+ (i.e. Ca²⁺).

Question 11.
What happens to an element ‘A’ if its atom gains two electrons ?
Answer:
It changes to a divalent anion (A^2-).

Question 12.
Why is a cation so named ?
Answer:
When electric current is passed through the solution of a salt like sodium chloride (NaCl), the positive ion (Na⁺) migrates towards cathode (negative electrode). It is therefore, called cation. Please remember that
• Positive ion migrating towards cathode on passing electric current is known as cation.
• Negative ion migrating towards anode on passing electric current is known as anion.

Question 13.
An element Z forms an oxide with formula Z₂O₃. What is its valency ?
Answer:
The valency of the element Z in Z₂O₃ is 3+.

Question 14.
The valency of an element A is 4. Write the formula of its oxide.
Answer:
The formula of the oxide is A₂O₄ or AO₂.

Question 15.
An element X has valency 3 while the element Y has valency 2. Write the formula of the compound between X and Y.
Answer:
The formula of the compound between X and Y is X₂Y₃.

Question 16.
Formula of the carbonate of a metal M is M₂CO₃. Write the fomula of its chloride.
Answer:
The valency of the metal (M) in M₂CO₃ is (1+) i.e. metal exists as M+ ion. Therefore, the formula of metal chloride is MCl.

Question 17.
What do you understand from the statement “relative atomic mass of sulphur is 32”. (CBSE 2012)
Answer:
This means that an atom of sulphur is 32 times heavier as compared to 1/12 of the mass of 1 atom of C — 12(1 u).

Question 18.
Calculate the formula unit mass of CaCl₂.
Answer:
Formula unit mass of CaCl₂ (Calcium chloride)
= (1 x Atomic mass of Ca) + (2 x Atomic mass of Cl)
= (1 x 40 u) + (2 x 35.5 u) = 111 u.

Question 19.
Which of the following represents the correct chemical formula ?
(a) NaSO₄
(b) CaPO₄
(c) ZnS
(d) AlSO₄.
Answer:
The formula (c) represents the correct formula. Both the ions are divalent i.e. Zn²⁺ and S^2-. The name of the compound is zinc sulphide.

Question 20.
Sample A contains one gram molecules of oxygen molecules and sample B contains one mole of oxygen molecules. What is the ratio of the number of molecules in both the sample ?
Answer:
One gram molecules and one gram mole contain the same number of molecules (6.022 x 10²³). Therefore, the ratio is 1 : 1.

Question 21.
Gram molecular mass of ammonia (NH₃) is 17 g. Is it correct to regard it as formula unit mass also ?
Answer:
No, it is not correct. Ammonia exists in molecular form and is not an ionic compound made up of cation and anion. Therefore, it cannot have formula unit mass. It has only molecular mass.

Question 22.
Give one example each of polyatomic element and polyatomic ion.
Answer:
Polyatomic element (P₄) ; Polyatomic ion (SO₄^2-).

Question 23.
Name the element which is used as a reference for the atomic masses of the elements.
Answer:
1/12 of the mass of carbon atom taken as 12 u is used as a reference for the atomic masses of the elements.

Question 24.
Four samples of water [H₂O] are collected from different sources. Each sample on analysis was found to contain same percentage of oxygen. Which law of chemical combination is demonstrated by the above observation ?
(CBSE 2014)
Answer:
The law of constant combination is demonstrated by this observation.

SHORT ANSWER QUESTIONS

Question 25.
List the elements present in
(i) quick lime
(ii) sodium hydrogen carbonate.
Answer:
(i) The chemical name of quick lime is calcium oxide. Its chemical formula is CaO. Elements present are Ca and O.
(ii) The chemical formula of sodium hydrogen carbonate is NaHCO₃. The elements present are Na, H, C and O.

Question 26.
Cenvert into moles :
(i) 20 g of water
(ii) 20 g of carbon dioxide
Answer:
NCERT Solutions For Class 9 Science Chapter 3 Atoms and Molecules 16

Question 27.
(a) How many moles are present in 11.5 g of sodium ?
(b) The mass of an atom of element (X) is 2.0 x 10^-23 g. Calculate its atomic mass.
Answer:
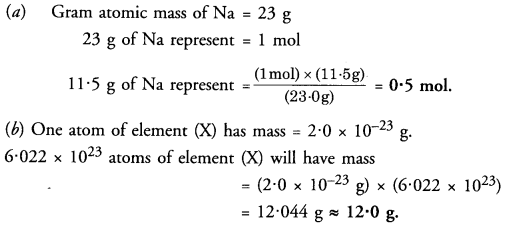
NCERT Solutions For Class 9 Science Chapter 3 Atoms and Molecules 17

Question 28.
(a) How many particles are represented by 0.25 mole of an element ?
(b) Out of 4 g of methane (CH₄) and llg of CO₂, which has more molecules ?
Answer:
NCERT Solutions For Class 9 Science Chapter 3 Atoms and Molecules 18

Question 29.
What is the number of molecules present in 1.5 mole of ammonia (NH₃) ?
Answer:
NCERT Solutions For Class 9 Science Chapter 3 Atoms and Molecules 19

Question 30.
Write the chemical symbols of two elements
(a) Which are formed from the first letter of the elements name.
(b) Whose name has been taken from the names of the elements in Latin.
Answer:
(a) Boron (B), carbon (C)
(b) Argentum (Ag), Kalium (K).

Question 31.
(a) Four samples of carbon dioxide (CO₂) were prepared by using different methods. Each sample on analysis was found to contain 27.27% carbon by mass. Name the law which is in agreement with this observation.
(b) Explain why the number of atoms in one mole of hydrogen gas is double the number of atoms in one mole of helium gas.
Answer:
(a) Carbon dioxide consists of elements carbon and oxygen. Since the percentage of carbon in each sample is fixed, that of oxygen must be also fixed. This is according to law of constant proportions.
(b) Hydrogen gas is diatomic in nature (H₂) while helium gas is monoatomic (He). As a result, the number of atoms in one mole of hydrogen. (2 x N_A) are expected to be double as compared to number of atoms in one mole of helium (N_A).

Question 32.
10²² atoms of an element ‘X’ are found to have a mass of 930 mg. Calculate the molar mass of the element ‘X’?
Answer:
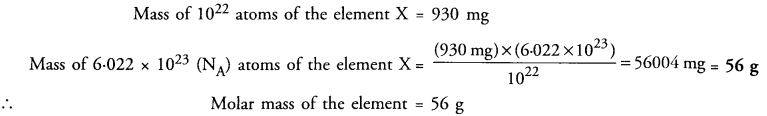
NCERT Solutions For Class 9 Science Chapter 3 Atoms and Molecules 20

Question 33.
(a) If the valency of carbon is 4 and that of sulphur is 2, write the formula of the compound formed between carbon and sulphur atoms. Also name the compound.
(b) What is wrong with the statement T mole of hydrogen ?
Answer:
(a) The formula of compound can be written by exchanging the valencies (cross-over). Therefore, the expected formula is C₂S₄ or CS₂. The compound is called carbon disulphide.
(b) The statement is not correct. We must always write whether hydrogen is in atomic form or molecular form. The correct statement is :

Question 34.
T mole of hydrogen atoms or one mole of hydrogen molecules.
Identify the cations and anions in the following compounds :
(a) CH₃COONa
(b) NH₃ (c) NH₄Cl
(d) SrCl₂.
Answer:
(a) CH₃COO^–, Na⁺
(b) It is a molecular compound
(c) NH₄⁺ ,Cl^– (d) Sr²⁺, 2Cl^–

Question 35.
Classify the following based on atomicity
(a) O₃
(b) P₄
(c) S₈. (CBSE 2012)
Answer:
Atomicity is the number of atoms present in one molecule of an element. Based upon this, the atomicity of different molecules may be expressed as :
(a) 3
(b) 4
(c) 8.

Question 36.
Give the formulae of the compounds that will be formed from the following sets of elements.
(a) Calcium and fluorine
(b) Magnesium and oxygen
(c) Sodium and sulphur
(d) Carbon and chlorine
(e) Carbon and sulphur
(f) Nitrogen and hydrogen.
Answer:
(a) CaF₂
(b) MgO
(c) Na₂S
(d) CCl₄
(e) CS₂
(f) NH₃.

Question 37.
Which of the following symbols of elements are incorrect. Write correct symbols
(a) Iron (Ir)
(b) Gold (Au)
(c) Manganese (M)
(d) Potassium (Po)
(e) Zinc (ZN)
(f) Calcium (Ca).
Answer:
(a) Iron (Fe)
(c) Manganese (Mn)
(d) Potassium (K)
(e) Zinc (Zn).

Question 38.
Verify by calculation that :
4 moles of CO₂ and 6 moles of H₂O do not have same mass in grams.
Answer:
Molar mass of CO₂ = 12 + 2 x 16 = 44 g
1 mole of CO₂ has mass = 44 g
4 moles of CO₂
have mass = 44 x 4 = 176 g
Molar mass of H₂O = 2 x 1 + 16 =18 g
1 mole of H₂O has mass = 18 g
6 moles of H₂O have mass = 6 x 18 = 108 g.
This shows that these have different masses in grams.

Question 39.
A sample of vitamin C contains 2.48 x 10²⁵ oxygen atoms. How many moles of oxygen atoms are present in the sample ?
Answer:
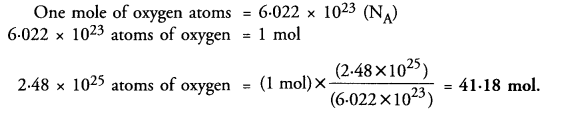
NCERT Solutions For Class 9 Science Chapter 3 Atoms and Molecules 21

Question 40.
Calculate the total number of ions in 0.585 g of sodium chloride.
Answer:
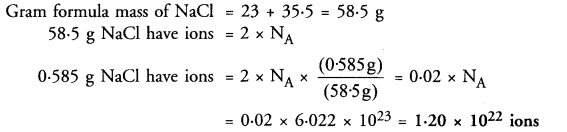
NCERT Solutions For Class 9 Science Chapter 3 Atoms and Molecules 22

Question 41.
A flask contains 4.4 g of CO₂ gas. Calculate
(a) How many moles of CO₂ gas does it contain ?
(b) How many molecules of CO₂ gas are present in the sample.
(c) How many atoms of oxygen are present in the given sample.
(Atomic mass of C = 12 u. O = 16 u)
Answer:
NCERT Solutions For Class 9 Science Chapter 3 Atoms and Molecules 23

Question 42.
Determine the molecular mass of :
(i) NH₄OH
(ii) K₂CO₃
(iii) CH₃COOH Given atomic masses :
H = 1.0 u ; O = 16.0 u ; C = 12.0 ; K = 39.0 u ; N = 14.0 u
Answer:
(i) Molecular mass of NH₄OH
= Atomic mass of N + 5 x (Atomic mass of H) + Atomic mass of O
= 14 + 5 x 1 + 16 = 14 + 5 + 16 = 35 u
(ii) Molecular mass of K₂CO₃
= 2 x (Atomic mass of K) + Atomic mass of C + 3 x (Atomic mass of O)
= 2 x 39 + 12 + 3 x 16 = 138 u
(iii) Molecular mass of CH₃COOH
= 2 x (Atomic mass of C) + 4 x (Atomic mass of H) + 2 x (Atomic mass of O)
= 2 x 12 + 4 x 1+2 x 16 = 60 u

Question 43.
(a) What is Avogadro Constant ?
(b) Calculate the number of particles present in 56 g of N₂ molecule.
Answer:
(a) Avogadro’s number is the number of particles (atoms, ions, molecules etc.) present in one mole of any substance. It is denoted either as N_A or as N_Q. The number is also called Avogadro’s constant because its value is fixed (6.022 x 10²³) irrespective of the nature of the particles.
(b) Molar mass of N₂ = 14 x 2 = 28 g
28 g of N₂ have molecules or particles = N_A = 6.022 x 10²³56 g of N₂ have molecules or particles = N_A = 6.022 x 10²³ x 2 = 1.204 x 10²⁴

Question 44.
(a) An element ‘X’ exhibits variable valencies 3 and 5. Write the formulae of the chlorides of the element.
(b) What is the ratio by mass of the elements present in the chemical formula of magnesium oxide.
Answer:
(a) The formulae of the chlorides of the element ‘X’ = XCl₅ and XCl₃.
(b) The chemical formula of magnesium oxide is MgO. The elements are present in the ratio of 24 : 16 or 3 : 2.

Question 45.
Give the example of trivalent cation and monovalent anion. Write the formula of the compound formed by their combination. .
Answer:
Trivalent cation : Al³⁺ ; Monovalent anion : Cl^–
Formula of the compound : AlCl₃.

Question 46.
(a) State the law of conservation of mass
(b) What mass of silver nitrate will react with 5.85 g of sodium chloride to produce 14.35 g of silver chloride and 8.5 g of sodium nitrate if the law of conservation of mass is true ?
Answer:
(a) The total mass of the products in a physical change or a chemical reaction is equal to the total mass of the reactants that have combined. The law may also be stated in another form. The mass can neither he created nor destroyed in a physical change or a chemical reaction.
(b) The chemical reaction leading to products is :
Mass of reactants = x g + 5.85 g Mass of products = 14.35 g + 8.5 g According to law of conservation of mass
Mass of reactants = Mass of products . (x + 5.85) g = (14.35 + 8.5) g
x = (22.85 – 5.85) g = 17.0 g

LONG ANSWER QUESTIONS

Question 47.
(a) The mass of one molecule of a substance is 4.65 x 10^-23 g. What is its molecular mass ? What could this substance be ?
(b) Which have more molecules? 10 g of sulphur dioxide (SO₂) or 10 g of oxygen (O₂) ?
Answer:
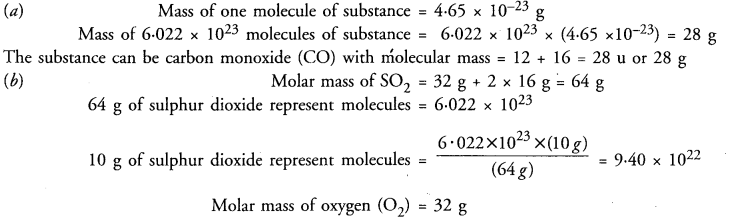
NCERT Solutions For Class 9 Science Chapter 3 Atoms and Molecules 24

Question 48.
Which has more atoms ?
(a) 10 g of nitrogen (N₂)
(b) 10 g of ammonia (NH₃)
Answer:
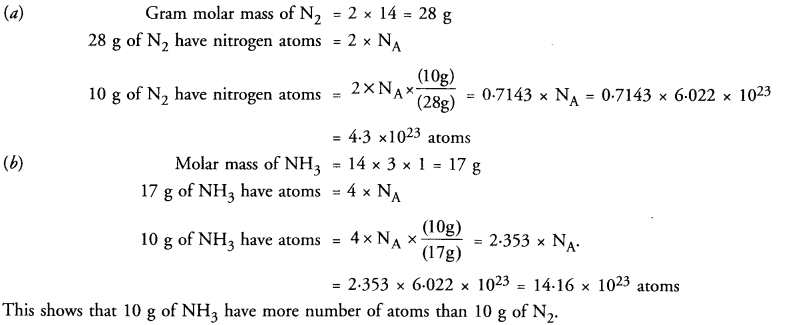
NCERT Solutions For Class 9 Science Chapter 3 Atoms and Molecules 26

Question 49.
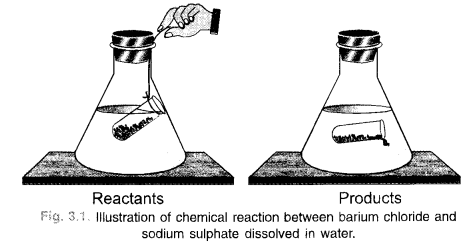
(a) Explain with the help of a labelled diagram an activity for the verification of law of conservation of mass.
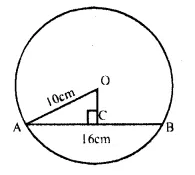
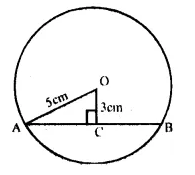
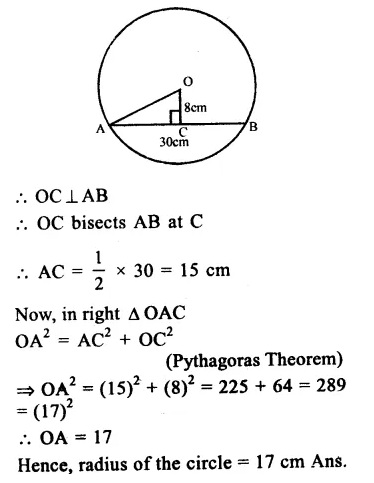
(b) Find the number of atoms present in 100 g of sodium and 100 g of iron. (Given that Na = 23 u ; Fe = 56 u ;
Answer:
(a) The total mass of the products in a physical change or a chemical reaction is equal to the total mass of the reactants that have combined. The law may also be stated in another form. The mass can neither he created nor destroyed in a physical change or a chemical reaction.
In other words, the mass remains unchanged or conserved in a chemical reaction. The law is also known as the Law of Indestructibility of Matter.
Explanation : Let us try to analyse as to what happens in a chemical reaction. To understand the same, let us consider a chemical reaction between barium chloride and sodium sulphate. When the solutions of these reactants prepared separately in water are mixed, the following chemical reaction takes place :
Barium chloride + Sodium sulphate———– > Barium sulphate + Sodium chloride (white precipitate)
If we look at this reaction, we find that the exchange of constituents has taken place between the reactants, i.e. chloride part of barium chloride has been exchanged by sulphate part of sodium sulphate. As such, no loss or gain in mass is expected. In other words, the mass remains conserved or does not change.
NCERT Solutions For Class 9 Science Chapter 3 Atoms and Molecules 27

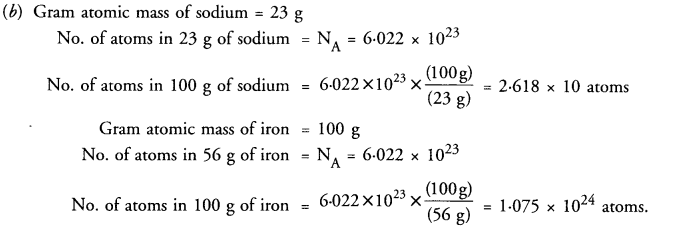
Question 50.
(a) Give one point of difference between an atom and an ion.
(b) Give one example each of a polyatomic cation and a polyatomic anion.
(c) Identify the correct chemical name of FeSO₄ from the given names Ferrous sulphate, Ferrous sulphide, Ferrous sulphite.
(d) Write the chemical formula for the chloride of magnesium.
Answer:
(a) An atom is always neutral in the sense that it does not carry any charge. An ion carries either positive charge (cation) or negative charge (anion).
(b) Ammonium (NH₄)⁺ ion is a polyatomic cation while sulphate (SO₄)^2- ion is a polyatomic anion.
(c) Correct chemical name of FeSO₄ is ferrous sulphite.
(d) Chemical formula for the chloride of magnesium is MgCl₂.

Question 51.
(a) What do the following observations stand for ?
(i) 2O
(ii) 3O₂
(b) Which amongst the following has more number of atoms and how much ?
(i) 11.5 g of sodium
(ii) 15.0 g of calcium
Answer:
(a) (i) 2O represent two atoms of oxygen (or the gram atoms of oxygen
(ii) 3O₂ represent three molecules of oxygen or three gram moles of oxygen.
NCERT Solutions For Class 9 Science Chapter 3 Atoms and Molecules 29

NCERT Solutions for Class 9 Science Chapter 3 Atoms and Molecules

Get 100 percent accurate NCERT Solutions for Class 9 Science Chapter 3 (Atoms and Molecules) explained by expert Science teachers. We provide solutions for the questions given in Class 9 Science textbook as per CBSE Board guidelines from the latest NCERT book for Class 9 Science. The topics and sub-topics in Chapter 3 Atoms and Molecules

3.1 Laws of Chemical Combination
3.1.1 LAW OF CONSERVATION OF MASS
3.1.2 LAW OF CONSTANT PROPORTIONS
3.2 What is an Atom?
3.2.1 WHAT ARE THE MODERN DAY SYMBOLS OF ATOMS OF DIFFERENT ELEMENTS?
3.2.2 ATOMIC MASS
3.2.3 HOW DO ATOMS EXIST?
3.3 What is a Molecule?
3.3.1 MOLECULES OF ELEMENTS
3.3.2 MOLECULES OF COMPOUNDS
3.3.3 WHAT IS AN ION?
3.4 Writing Chemical Formulae
3.4.1 FORMULAE OF SIMPLE COMPOUNDS
3.5 Molecular Mass and Mole Concept
3.5.1 MOLECULAR MASS
3.5.2 FORMULA UNIT MASS
3.5.3 MOLE CONCEPT.

We cover all exercises in the chapter given below:-

EXERCISE 3.1 – 4 Questions with Solutions
EXERCISE 3.2 – 2 Questions with Solutions
EXERCISE 3.3 – 4 Questions with Solutions
EXERCISE 3.4 – 2 Questions with Solutions
EXERCISE 3.5 – 2 Questions with Solutions
EXERCISE 3.6 – 11 Questions with Solutions.

Download the free PDF of Chapter 3 Atoms and Molecules or save the solution images and take the print out to keep it handy for your exam preparation.

Hope given NCERT Solutions for Class 9 Science Chapter 3 are helpful to complete your science homework.

If you have any doubts, please comment below. Learn Insta try to provide online science tutoring for you.

RD Sharma Class 9 Solutions Chapter 7 Introduction to Euclid’s Geometry Ex 7.1

January 5, 2022June 21, 2018 by Prasanna

RD Sharma Class 9 Solutions Chapter 7 Introduction to Euclid’s Geometry Ex 7.1

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 7 Introduction to Euclid’s Geometry Ex 7.1

Other Exercises

Question 1.
Express the following linear equations in the form ax + by + c = 0 and indicate the values of a, b and c in each case:
(i) -2x + 3y = 12
(ii) x-\(\frac { y }{ 2 }\) -5 = 0
(iii) 2x + 3y = 9.35
(iv) 3x = -7y
(v) 2x + 3 = 0
(vi) y – 5 = 0
(vii) 4 = 3x
(viii) y = \(\frac { x }{ 2 }\)
Solution:
(i) -2x + 3y = 12
⇒ -2x + 3y – 12 = 0
Here a -2, b = 3, c = – 12
(ii) x – \(\frac { y }{ 2 }\) -5 = 0
Here a = 1, b =\(\frac { 1 }{ 2 }\) ,c = -5
(iii) 2x + 3y = 9.35
⇒ 2x + 3y – 9.35 = 0
Here a = 2, b = 3, c = – 9.35
(iv) 3x = -7y
⇒ 3x + 7y + 0 = 0
Here a = 3, b = 7,c = 0
(v) 2x + 3 = 0
⇒ 2x + 0y + 3 = 0
Here a = 2, b = 0, c = 3
(vi) y-5 = 0 ⇒ ox+y-5 = 0
Here a = 0, b = 1, c = -5
(vii) 4 = 3x
⇒ 3x – 4 = 0
⇒ 3x + 0y – 4 = 0
Here a = 3, b = 0, c = -4
(Viii) y= \(\frac { x }{ 2 }\)
⇒ \(\frac { x }{ 2 }\) – y+ 0 = 0
⇒ x-2y + 0 = 0
Here a = 1, y = -2, c = 0

Question 2.
Write each of the following as an equation in two variables.
(i) 2x = -3
(ii) y = 3
(iii) 5x = \(\frac { 7 }{ 2 }\)
(iv) y =\(\frac { 3 }{ 2 }\)x
Solution:
(i) 2x = -3⇒ 2x + 3 = 0
⇒ 2x + 0y + 3 = 0
(ii) y= 3 ⇒ y-3=0
⇒ 0x+ y-3 = 0
(iii) 5x =\(\frac { 7 }{ 2 }\) ⇒ 10x = 7
⇒ 10x + 0y – 7 = 0
(iv) y=\(\frac { 3 }{ 2 }\)x⇒2y = 3x
⇒ 3x – 2y + 0 = 0

Question 3.
The cost of ball pen is ₹5 less than half of the cost of fountain pen. Write this statement as a linear equation in two variables.
Solution:
Let cost of a fountain pen = ₹x
and cost of ball pen = ₹y
∴ According to the condition,
y = \(\frac { x }{ 2 }\) -5⇒ 2y = x – 10
⇒ x – 2y – 10 = 0

Hope given RD Sharma Class 9 Solutions Chapter 7 Introduction to Euclid’s Geometry Ex 7.1 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials MCQS

January 5, 2022June 21, 2018 by Prasanna

RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials MCQS

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials MCQS

Other Exercises

Mark the correct alternative in each of the following:
Question 1.
If x – 2 is a factor of x² + 3 ax – 2a, then a =
(a) 2
(b) -2
(c) 1
(d) -1
Solution:
∴ x – 2 is a factor of
f(x) = x² + 3 ax – 2a
∴ Remainder = 0
Let x – 2 = 0, then x = 2
Now f(2) = (2)² + 3a x 2 – 2a
= 4 + 6a – 2a = 4 + 4a
∴ Remainder = 0
∴ 4 + 4a = 0 ⇒ 4a = -4
⇒ a = \(\frac { -4 }{ 4 }\) = -1
∴ a= -1 (d)

Question 2.
If x³ + 6x² + 4x + k is exactly divisible by x + 2, then k =
(a) -6
(b) -7
(c) -8
(d) -10
Solution:
f(x) – x³ + 6x² + 4x + k is divisible by x + 2
∴ Remainder = 0
Let x + 2 = 0, then x = -2
∴ f(-2) = (-2)³ + 6(-2)² + 4(-2) + k
= -8 + 24-8 + k = 8 + k
∴ x + 2 is a factor
∴ Remainder = 0                                 .
⇒ 8 + k= 0 ⇒ k = -8
k = -8                                                (c)

Question 3.
If x – a is a factor of x³ – 3x² a + 2a²x + b, then the value of b is
(a) 0
(b) 2
(c) 1
(d) 3
Solution:
∴ x – a is a factor of x³ – 3x² a + 2a²x + b
Let f(x) = x³ – 3x² a + 2a²x+ b
and x – a = 0, then x = a
f(a) = a³ – 3a².a + 2a².a + b
= a³ – 3a³ + 2a³ + b = b
∵ x – a is a factor of f(x)
∴ b = 0 (a)

Question 4.
If x¹⁴⁰ + 2x¹⁵¹ + k is divisible by x + 1, then the value of k is
(a) 1
(b) -3
(c) 2
(d) -2
Solution:
∴ x + 1 is a factor of f(x) = x¹⁴⁰ + 2x¹⁵¹ + k
∴ Remainder will be zero
Let x + 1 = 0, then x = -1
∴ f(-1) = (-1)¹⁴⁰ + 2(-1)¹⁵¹ + k
= 1 + 2 x (-1) + k {∵ 140 is even and 151 is odd}
=1-2+k=k-1
∵ Remainder = 0
∴ k – 1=0 ⇒ k=1 (a)

Question 5.
If x + 2 is a factor of x² + mx + 14, then m =
(a) 7
(b) 2
(c) 9
(d) 14
Solution:
x + 2 is a factor of(x) = x² + mx + 14
Let x + 2 = 0, then x = -2
f(-2) = (-2)² + m{-2) + 14
= 4 – 2m + 14 = 18 – 2m
∴ x + 2 is a factor of f(x)
∴ Remainder = 0
⇒ 18 – 2m = 0
2m = 18 ⇒ m = \(\frac { 18 }{ 2 }\) = 9                       (c)

Question 6.
If x – 3 is a factor of x² – ax – 15, then a =
(a) -2
(b) 5
(c) -5
(d) 3
Solution:
x – 3 is a factor of(x) = x² – ax – 15
Let x – 3 = 0, then x = 3
∴ f(3) = (3)² – a(3) – 15
= 9 -3a- 15
= -6 -3a
∴ x – 3 is a factor
∴ Remainder = 0
-6 – 3a = 0 ⇒ 3a = -6
∴ a = \(\frac { -6 }{ 3 }\) = -2 (a)

Question 7.
If x⁵¹ + 51 is divided by x + 1, the remainder is
(a) 0
(b) 1
(c) 49
(d) 50
Solution:
Letf(x) = x⁵¹ + 51 is divisible by x + 1
Let x+1=0, then x = -1
∴ f(-1) = (-1)⁵¹ + 51 =-1+51 (∵ power 51 is an odd integer)
= 50 (d)

Question 8.
If x+ 1 is a factor of the polynomial 2x² + kx, then k =
(a) -2
(b) -3
(c) 4
(d) 2
Solution:
∴ x + 1 is a factor of the polynomial 2x² + kx
Let x+1=0, then x = -1
Now f(x) = 2x² + kx
∴ Remainder =f(-1) = 0
= 2(-1)² + k(-1)
= 2 x 1 + k x (-1) = 2 – k
∴ x + 1 is a factor of f(x)
∴ Remainder = 0
∴ 2 – k = 0 ⇒ k = 2                                 (d)

Question 9.
If x + a is a factor of x⁴ – a²x² + 3x – 6a, then a =
(a) 0
(b) -1
(c) 1
(d) 2
Solution:
x + a is a factor o f(x) = x⁴– a²x² + 3x – 6a
Let x + a = 0, then x = -a
Now, f(-a) – (-a)⁴ -a²(-a)² + 3 (-a) – 6a
= a⁴-a⁴-3a-6a = -9a
∴ x + a is a factor of f(x)
∴Remainder = 0
∴ -9a = 0 ⇒ a = 0                               (a)

Question 10.
The value of k for which x – 1 is a factor of 4x³ + 3x² – 4x + k, is
(a) 3
(b) 1
(c) -2
(d) -3
Solution:
x- 1 is a factor of f(x) = 4x³ + 3x² – 4x + k
Let x – 1 = 0, then x = 1
f(1) = 4(1 )³ + 3(1)² – 4 x 1 + k
= 4+3-4+k=3+k
∴ x- 1 is a factor of f(x)
∴ Remainder = 0
∴ 3 + k = 0 ⇒ k = -3 (d)

Question 11.
If x+2 and x-1 are the factors of x³+ 10x² + mx + n, then the values of m and n are respectively
(a) 5 and-3
(b) 17 and-8
(c) 7 and-18
(d) 23 and -19
Solution:
x+ 2 and x – 1 are the factors of
f(x) = x³ + 10x² + mx + n
Let x + 2 = 0, then x = -2
∴ f(-2) = (-2)³ + 10(-2)² + m(-2) + n
= -8 + 40 – 2m + n = 32 – 2m + n
∴ x + 2 is a factor of f(x)
∴ Remainder = 0
∴ 32 – 2m + n = 0 ⇒ 2m – n = 32   …(i)
Again x – 1 is a factor of f(x)
Let x-1=0, then x= 1
∴ f(1) = (1)³ + 10(1)² + m x 1 +n
= 1 + 10+ m + n =m + n+11
∴ x- 1 is a factor of f(x)
∴ m + n+ 11=0 ⇒ m+n =-11 …(ii)
Adding (i) and (ii),
3m = 32 – 11 = 21
⇒ m = \(\frac { 21 }{ 3 }\) = 7
and n = -11 – m = m = 7, n = -18
∴ m= 7, n = -18 (c)

Question 12.
Let f(x) be a polynomial such that f( \(\frac { -1 }{ 2 }\) )= 0, then a factor of f(x) is
(a) 2x – 1
(b) 2x + b
(c) x- 1
(d) x + 1
Solution:
RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials MCQS Q12.1

Question 13.
When x³ – 2x² + ax – b is divided by x² – 2x-3, the remainder is x – 6. The value of a and b are respectively.
(a) -2, -6
(b) 2 and -6
(c) -2 and 6
(d) 2 and 6
Solution:
Let f(x) = x³ – 2x² + ax – b
and Dividing f(x) by x² – 2x + 3
Remainder = x – 6
Let p(x) = x³ – 2x² + ax – b – (x – 6) or x³– 2x² + x(a – 1) – b + 6 is divisible by x² – 2x+ 3 exactly
Now, x²-2x-3 = x²-3x + x- 3
= x(x – 3) + 1(x – 3)
= (x – 3) (x + 1)
∴ x – 3 and x + 1 are the factors of p(x)
Let x – 3 = 0, then x = 3
∴ p(3) = (3)³ – 2(3)² + (a-1)x3-b + 6
= 27-18 + 3a-3-b + 6
= 33-21+3 a-b
= 12 + 3 a-b
∴ x – 3 is a factor
∴ 12 + 3a-b = 0 ⇒ 3a-b = -12               …(i)
Again let x + 1 = 0, then x = -1
∴p(-1) = (-1)³ – 2(-l)² + (a – 1) X (-1) – b + 6
= -1-2 + 1 – a – 6 + 6
= 4 – a- b
∴ x + 1 is a factor
4-a-b = 0 ⇒ a + b = 4                  …(ii)
Adding (i) and (ii),
4 a = -12 + 4 = -8 ⇒ a = \(\frac { -8 }{ 4 }\) = -2
From (ii),
and -2 + 6 = 4⇒ 6 = 4 + 2 = 6
∴ a = -2, h = 6                       (b)

Question 14.
One factor of x⁴ + x² – 20 is x² + 5, the other is
(a) x² – 4
(b) x – 4
(c) x²-5
(d) x + 4
Solution:

RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials MCQS Q14.1

Question 15.
If (x – 1) is a factor of polynomial fix) but not of g(x), then it must be a factor of
(a) f(x) g(x)
(b) -f(x) + g(x)
(c) f(x) – g(x)
(d) {f(x) + g(x)}g(x)
Solution:
∴ (x – 1) is a factor of a polynomial f(x)
But not of a polynomial g(x)
∴ (x – 1) will be the factor of the product of f(x) and g(x) (a)

Question 16.
(x + 1) is a factor of xⁿ + 1 only if
(a) n is an odd integer
(b) n is an even integer
(c) n is a negative integer
(d) n is a positive integer
Solution:
∴ (x + 1) is a factor of xⁿ+ 1
Let x + 1 = 0, then x = -1
∴ f(x) = xⁿ + 1
and f(-1) = (-1)ⁿ + 1
But (-1)ⁿ is positive if n is an even integer and negative if n is an odd integer and (-1)ⁿ +1=0 {∵ x + 1 is a factor of(x)}
(-1)ⁿ must be negative
∴ n is an odd integer (a)

Question 17.
If x² + x + 1 is a factor of the polynomial 3x³ + 8x² + 8x + 3 + 5k, then the value of k is
(a) 0
(b) \(\frac { 2 }{ 5 }\)
(c) \(\frac { 5 }{ 2 }\)
(d) -1
Solution:
x² + x + 1 is a factor of
f(x) = 3x³ + 8x² + 8x + 3 + 5k
Now dividing by x² + x + 1, we get
RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials MCQS Q17.1

Question 18.
If (3x – 1)⁷ = a₇x^₇ + a₆x⁶ + a₅x⁵ + … + a₁x + a₀, then a₇ + a₆ + a₅ + … + a₁ + a₀ =
(a) 0
(b) 1
(c) 128
(d) 64
Solution:
f(x) = [3(1) – 1]⁷ = a₇x⁷ + a₆x⁶ + a₅x⁵ + … + a₁x + a₀Let x = 1, then
f(1) = (3x- 1)⁷ = a₇(1)⁷ + a₆(1)⁶ + a₅(1)⁵ + … + a₁ x 1 + a₀⇒ (3 – 1)⁷ = a₇ x 1 + a₆ x 1+ a₅ x 1 + … + a₁x 1 +a₀⇒ (2)⁷ = a₇ + a₆ + a₅ + … + a₁ +a₀∴ a₇ + a₆ + a₅ + … + a₁ + a₀= 128 (c)

Question 19.
If both x – 2 and x – \(\frac { 1 }{ 2 }\) are factors of px² + 5x + r, then
(a) p = r
(b) p + r = 0
(c) 2p + r = 0
(d) p + 2r = 0
Solution:
RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials MCQS Q19.1

Question 20.
If x² – 1 is a factor of ax⁴ + bx³ + cx² + dx + e, then
(a) a + c + e- b + d
(b)a + b + e = c + d
(c)a + b + c = d+ e
(d)b + c + d= a + e
Solution:
X² – 1 is a factor of ax⁴ + bx³ + cx² + dx + e
⇒ (x + 1), (x – 1) are the factors of ax⁴ + bx³+ cx² + dx + e
Let f(x) = ax⁴ + bx³ + cx² + dx + e
and x + 1 = 0 then x = -1
∴ f(-1) = a(-1)⁴ + b(-1)³ + c(-1)² + d(-1) + e
= a- b + c- d+ e
∴ x + 1 is a factor of f(x)
∴ a-b + c- d+e = 0
⇒ a + c + e = b + d (a)

Hope given RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials MCQS are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 9 Solutions Chapter 10 Area Ex 10A

January 5, 2022June 21, 2018 by Prasanna

RS Aggarwal Class 9 Solutions Chapter 10 Area Ex 10A

These Solutions are part of RS Aggarwal Solutions Class 9. Here we have given RS Aggarwal Class 9 Solutions Chapter 10 Area Ex 10A.

Question 1.
Solution:
Given : In the figure, ABCD is a quadrilateral and
AB = CD = 5cm
RS Aggarwal Class 9 Solutions Chapter 10 Area Ex 10A Q1.1

Question 2.
Solution:
In ||gm ABCD,
AB = 10cm, altitude DL = 6cm
and BM is altitude on AD, and BM = 8 cm.
RS Aggarwal Class 9 Solutions Chapter 10 Area Ex 10A Q2.1

Question 3.
Solution:
Diagonals of rhombus are 16cm and 24 cm.
Area = \(\frac { 1 }{ 2 } \) x product of diagonals
= \(\frac { 1 }{ 2 } \) x 1st diagonal x 2nd diagonal
= \(\frac { 1 }{ 2 } \) x 16 x 24
= 192 cm² Ans.

Question 4.
Solution:
Parallel sides of a trapezium are 9cm and 6cm and distance between them is 8cm
RS Aggarwal Class 9 Solutions Chapter 10 Area Ex 10A Q4.1

Question 5.
Solution:
from the figure
(i) In ∆ BCD, ∠ DBC = 90°
RS Aggarwal Class 9 Solutions Chapter 10 Area Ex 10A Q5.1

Question 6.
Solution:
In the fig, ABCD is a trapezium. AB || DC
AB = 7cm, AD = BC = 5cm.
Distance between AB and DC = 4 cm.
i.e. ⊥AL = ⊥BM = 4cm.
RS Aggarwal Class 9 Solutions Chapter 10 Area Ex 10A Q6.1

Question 7.
Solution:
Given : In quad. ABCD. AL⊥BD and CM⊥BD.
To prove : ar(quad. ABCD)
RS Aggarwal Class 9 Solutions Chapter 10 Area Ex 10A Q7.1

Question 8.
Solution:
In quad. ABCD, BD is its diagonal and AL⊥BD, CM⊥BD
RS Aggarwal Class 9 Solutions Chapter 10 Area Ex 10A Q8.1

Question 9.
Solution:
Given : ABCD is a trapezium in which AB || DC and its diagonals AC and BD intersect each other at O.
To prove : ar(∆ AOD) = ar(∆ BOC)
RS Aggarwal Class 9 Solutions Chapter 10 Area Ex 10A Q9.1

Question 10.
Solution:
Given : In the figure,
DE || BC.
RS Aggarwal Class 9 Solutions Chapter 10 Area Ex 10A Q10.1

Question 11.
Solution:
Given : In ∆ ABC, D and E are the points on AB and AC such that
ar( ∆ BCE) = ar( ∆ BCD)
To prove : DE || BC.
Proof : (∆ BCE) = ar(∆ BCD)
But these are on the same base BC.
Their altitudes are equal.
Hence DE || BC
Hence proved.

Question 12.
Solution:
Given : In ||gm ABCD, O is any. point inside the ||gm. OA, OB, OC and OD are joined.
RS Aggarwal Class 9 Solutions Chapter 10 Area Ex 10A Q12.1

Question 13.
Solution:
Given : In quad. ABCD.
A line through D, parallel to AC, meets ‘BC produced in P. AP in joined which intersects CD at E.
To prove : ar( ∆ ABP) = ar(quad. ABCD).
Const. Join AC
RS Aggarwal Class 9 Solutions Chapter 10 Area Ex 10A Q13.1

Question 14.
Solution:
Given : ∆ ABC and ∆ DBC are on the same base BC with points A and D on , opposite sides of BC and
ar( ∆ ABC) = ar( ∆ DBC).
RS Aggarwal Class 9 Solutions Chapter 10 Area Ex 10A Q14.1

Question 15.
Solution:
Given : In ∆ ABC, AD is the median and P is a point on AD
BP and CP are joined
To prove : (i) ar(∆BDP) = ar(∆CDP)
(ii) ar( ∆ ABP) = ar( ∆ ACP)
RS Aggarwal Class 9 Solutions Chapter 10 Area Ex 10A Q15.1

Question 16.
Solution:
Given : In quad. ABCD, diagonals AC and BD intersect each other at O and BO = OD
To prove : ar(∆ ABC) = ar(∆ ADC)
Proof : In ∆ ABD,
RS Aggarwal Class 9 Solutions Chapter 10 Area Ex 10A Q16.1

Question 17.
Solution:
In ∆ ABC,D is mid point of BC
and E is midpoint of AD and BE is joined.
RS Aggarwal Class 9 Solutions Chapter 10 Area Ex 10A Q17.1

Question 18.
Solution:
Given : In ∆ ABC. D is a point on AB and AD is joined. E is mid point of AD EB and EC are joined.
To prove : ar( ∆ BEC) = \(\frac { 1 }{ 2 } \) ar( ∆ ABC)
Proof : In ∆ ABD,
E is midpoint of AD
BE is its median
ar(∆ EBD) = ar(∆ ABE)
RS Aggarwal Class 9 Solutions Chapter 10 Area Ex 10A Q18.1

Question 19.
Solution:
Given : In ∆ ABC, D is midpoint of BC and E is die midpoint of BO is the midpoint of AE.
To prove that ar( ∆ BOE) = \(\frac { 1 }{ 8 } \) ar(∆ ABC).
RS Aggarwal Class 9 Solutions Chapter 10 Area Ex 10A Q19.1

Question 20.
Solution:
Given : In ||gm ABCD, O is any point on diagonal AC.
To prove : ar( ∆ AOB) = ar( ∆ AOD)
Const. Join BD which intersects AC at P
Proof : In ∆ OBD,
P is midpoint of BD
(Diagonals of ||gm bisect each other)
RS Aggarwal Class 9 Solutions Chapter 10 Area Ex 10A Q20.1

Question 21.
Solution:
Given : ABCD is a ||gm.
P, Q, R and S are the midpoints of sides AB, BC, CD, DA respectively.
PQ, QR, RS and SP are joined.
RS Aggarwal Class 9 Solutions Chapter 10 Area Ex 10A Q21.1

Question 22.
Solution:
Given : In pentagon ABCDE,
EG || DA meets BA produced and
CF || DB, meets AB produced.
To prove : ar(pentagon ABCDE) = ar(∆ DGF)
RS Aggarwal Class 9 Solutions Chapter 10 Area Ex 10A Q22.1

Question 23.
Solution:
Given ; A ∆ ABC in which AD is the median.
To prove ; ar( ∆ ABD) = ar( ∆ ACD)
Const : Draw AE⊥BC.
Proof : Area of ∆ ABD
RS Aggarwal Class 9 Solutions Chapter 10 Area Ex 10A Q23.1

Question 24.
Solution:
Given : A ||gm ABCD in which AC is its diagonal which divides ||gm ABCD in two ∆ ABC and ∆ ADC.
RS Aggarwal Class 9 Solutions Chapter 10 Area Ex 10A Q24.1

Question 25.
Solution:
Given : In ∆ ABC,
D is a point on BC such that
BD = \(\frac { 1 }{ 2 } \) DC
AD is joined.
RS Aggarwal Class 9 Solutions Chapter 10 Area Ex 10A Q25.1

Question 26.
Solution:
Given : In ∆ ABC, D is a point on BC such that
BD : DC = m : n
AD is joined.
RS Aggarwal Class 9 Solutions Chapter 10 Area Ex 10A Q26.1

Hope given RS Aggarwal Class 9 Solutions Chapter 10 Area Ex 10A are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.