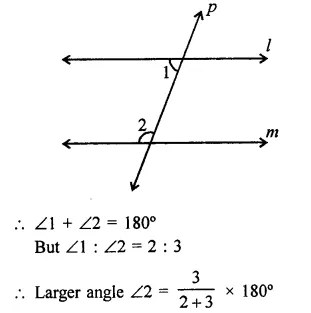
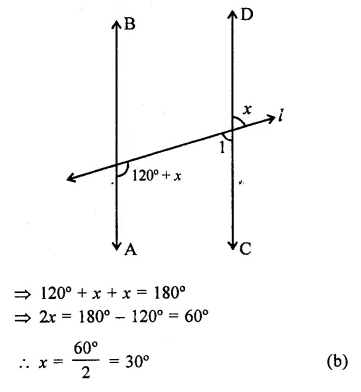
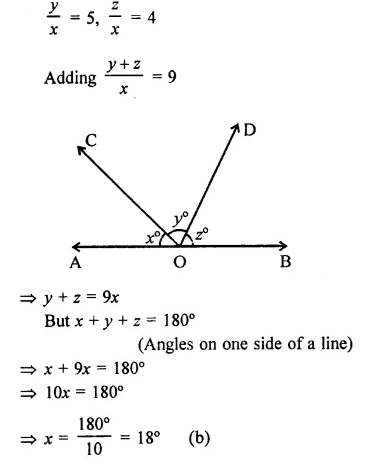
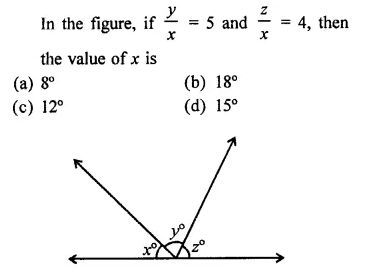NCERT Solutions for Class 9 Science Chapter 6 Tissues
These Solutions are part of NCERT Solutions for Class 9 Science. Here we have given NCERT Solutions for Class 9 Science Chapter 6 Tissues. LearnInsta.com provides you the Free PDF download of NCERT Solutions for Class 9 Science (Biology) Chapter 6 – Tissues solved by Expert Teachers as per NCERT (CBSE) Book guidelines. All Chapter 6 – Tissues Exercise Questions with Solutions to help you to revise complete Syllabus and Score More marks.
More Resources
- NCERT Solutions for Class 9 Science
- HOTS Questions for Class 9 Science
- Value Based Questions in Science for Class 9
- NCERT Exemplar Solutions for Class 9 Science
- Previous Year Question Papers for CBSE Class 9 Science
NCERT TEXT BOOK QUESTIONS
IN TEXT QUESTIONS
Question 1.
What is a tissue ?
Answer:
Tissue is a group of related cells that have a common origin and perform a common function.
Question 2.
What is the utility of tissues in multicellular organisms ?
Answer:
- Division of Labour: Tissues bring about division of labour in multicellular organisms. It increases efficiency.
- Higher Organisation: Tissues become organised to form organs and organ systems.
- Individual Cells: Work load of individual cells has decreased.
- Higher Survival: Because of division of labour, higher efficiency and organisation, the multicellular organisms have high survival.
Question 3.
Name types of simple tissues.
Answer:
Three – parenchyma, collenchyma and sclerenchyma. (Meristematic tissue is also a simple tissue).
Question 4.
Where is apical meristem found ?
Answer:
Apical meristem occurs at root and stem tips.
Question 5.
Which tissue makes up the husk of coconut ?
Answer:
Sclerenchyma.
Question 6.
What are the constituents of phloem ?
Answer:
Sieve tubes, companion cells, phloem parenchyma and phloem fibres.
Question 7.
Name the tissue responsible for movement of our body.
Answer:
Muscular tissue.
Question 8.
What does a neuron look-like ?
Answer:
A miniature tree with thin hair like parts arising from its ends.
Question 9.
Give three features of cardiac muscles.
Answer:
- Cells/Fibres: They are small, cylindrical, uninucleate striated with short lateral branches.
- Intercalated Discs: In the area of union becween the two adjacent cardiac muscle fibres, zig-zag junctions called intercalated discs develop. The intercalated discs function as impulse boosters.
- Rhythmic Contractions: The muscles are involuntary and nonfatigued which continue to contract and relax tirelessly throughout life.
Question 10.
What are the functions of areolar tissue ?
Answer:
- Packing: Areolar tissue provides packing material in various organs.
- Binding: It binds various structures with one another in such a way as to prevent their dislocation while allowing Macrophage limited movement.
- Covering: It provides covering over nerves, muscles and blood vessels.
- Repair: The tissue provides materials for repair of injury.
NCERT CHAPTER END EXERCISES
Question 1.
Define the term “tissue”.
Answer:
Tissue is a group of related cells that have a common origin and perform a common function.
Question 2.
How many types of elements together make up the xylem tissue ? Name them.
Answer:
Xylem tissue is formed of four types of elements. They are tracheids, vessels, xylem parenchyma and xylem fibres.
Question 3.
How are simple tissues different from complex tissues in plants ? (CCE 2014)
Answer:
Differences between Simple and Complex Tissues
| Simple Tissues | Complex Tissues |
| 1. Cells: A simple tissue is formed of only one type of cells. | A complex tissue is made of more than one type of cells. |
| 2. Activity: All the cells perform the same function. | The different cells perform different fractions of a function. |
| 3. Types: There are three types of simple plant tissues— . parenchyma, collenchyma and sclerenchyma. | There are two types of complex plant tissues— xylem and phloem. |
| 4. Function: They form primary structure of the plant. | They form transport system of the plant. |
Question 4.
Differentiate amongst parenchyma, collenchyma and sclerenchyma on the basis of the cell wall.
Answer:
| Parenchyma | Collenchyma | Sclerenchyma |
1. Thickness: The cell wall is thin. 2. Smoothness: It is smooth. 3. Nature: Wall is formed of cellulose. | It is thickened. It is unevenly thickened. The thickening is pectocellulosic. | It is thickened. The wall is uniformly thickened. The thickening is generally of lignin. |
Question 5.
What are the functions of stomata ?
Answer:
Functions of Stomata:
- Gaseous Exchange: Stomata are sites where exchange of gases (carbon dioxide and oxygen) occurs between the plant interior and external environment.
- Transpiration: Major part of transpiration occurs through stomata. Transpiration removes excess water and keeps plant surfaces cool even in bright sun.
- Regulation: They regulate both gaseous exchange and transpiration.
Question 6.
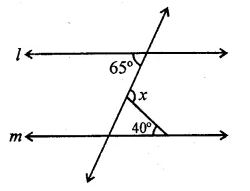
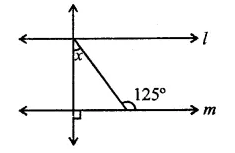
Diagramatically show the difference amongst three types of muscle fibres. (CCE 2014)
Answer:
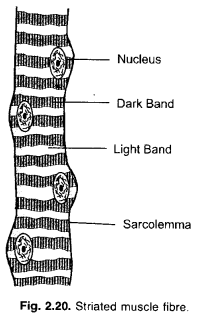
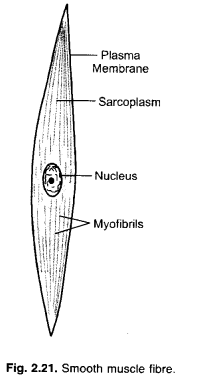
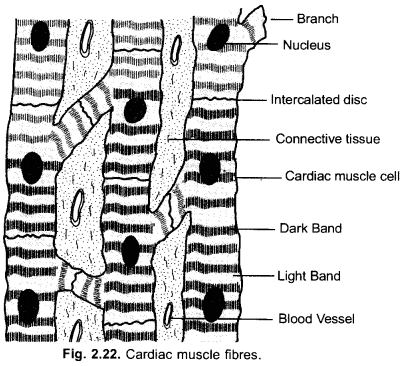
Question 7.
What is the specific function of cardiac muscle ?
Answer:
Rhythmic contraction and relaxation continuously throughout life without getting fatigued.
Question 8.
Differentiate amongst striated, unstriated and cardiac muscles on the basis of their structure and site/ location in the body.
Answer:
Striated Muscle Fibres | Smooth Muscle Fibres | Cardiac Muscle Fibres |
| 1. Cells. They are long cylindrical cells. | The fibres are elongated and spindleshaped. | The cells are small and cylindrical. |
| 2. Ends. The fibres have blunt ends. | The fibres have pointed ends. | The fibres have broad ends. |
| 3. Striations. They possess striations | Striations or light and dark bands | Striations are present but they are |
| or alternate light and dark bands. | are absent. | fainter than those of striated muscle fibres. |
| 4. Intercalated Discs and Cross | Intercalated discs and cross- | Intercalated discs and cross- |
| Connections. They are absent. | connections are absent. | connections are present. |
| 5. Nucleus. The muscle fibre is | Smooth muscle fibre is uninucleate. | The cells are uninucleate. Nucleus |
| multinucleate. Nuclei are oval in | Nucleus is centrally placed, oval or | in oval-rounded. It is centrally |
| outline. They occur peripherally below the sarcolemma. | elongated. | placed. |
| 6. Arrangement. They occur in bundles. | They generally form sheets. | They form a network. |
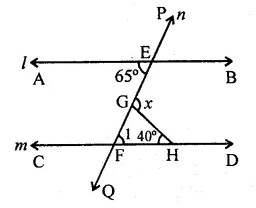
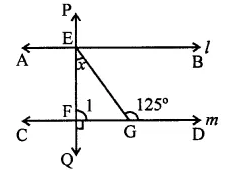
Question 9.
Draw a labelled diagram of a neuron. (CCE 2013)
Answer:
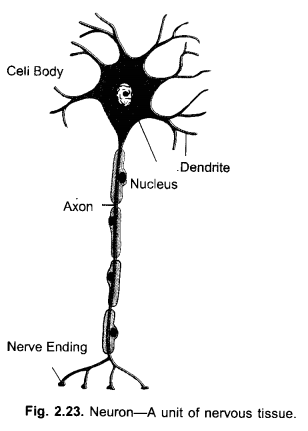
Question 10.
Name the following :
(a) Tissue that forms the inner lining of our mouth,
(b) Tissue that connects muscle to bone in humans.
(c) Tissue that transports food in plants.
(d) Tissue that stores fat in our body.
(e) Connective tissue with a fluid matrix.
(f) Tissue present in the brain.
Answer:
(a) Epithelial tissue
(b) Tendon
(c) Phloem
(d) Adipose
(e) Blood
(f) Nervous tissue.
Question 11.
Identify the types of tissue in the following : skin, bark of tree, bone, lining of kidney tubule, vascular bundle.
Answer:
(a) Skin— Epithelial tissue
(b) Bark of Tree— Cork (Protective tissue)
(c) Bone— Connective tissue with solid matrix
(d) Lining of Kidney Tubule— Epithelial tissue
(e) Vascular Bundle— Complex or vascular tissues, xylem and phloem.
Question 12.
Name the regions in which parenchyma tissue is present.
Answer:
It occurs in almost all nonwoody parts of the plants— cortex, pith, medullary rays of stem, cortex and pith of root, chlorenchyma of leaves, flowers, pith of fruits, etc. Epidermis is special type of parenchyma.
Question 13.
What is the role of epidermis in plants ?
Answer:
- Protection,
- Regulation of transpiration,
- Formation of insulating stationary air layer with the help of hair,
- Exchange of gases.
Question 14.
Flow does the cork act as a protective tissue ?
Answer:
Cork acts as a protective layer because its cells are dead, filled with tannins, resin and air, impermeable due to deposition of suberin over the cell walls and absence of intercellular spaces. It is insulating (heat proof), fire proof, shock proof, water proof and repellent to microbes and animals.
Question 15.
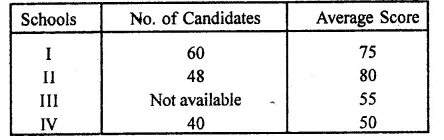
Complete the table :
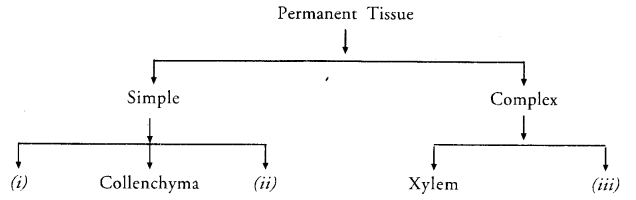
Answer:
(i) Parenchyma
(ii) Sclerenchyma
(iii) Phloem.
SELECTION TYPE QUESTIONS
Alternate Response Type Questions
(True/False, Right/Wrong, Yes/No)
Question 1.
Vacuoles are absent in meristematic plant cells.
Question 2.
Sderenchyma has irregularly thickened cells.
Question 3.
Absorptive surface areas of roots are increased by the presence of root hair.
Question 4.
Cells of connective tissue are compactly packed with no intercellular spaces.
Question 5.
Cardiac muscles undergo rhythmic contraction and relaxation throughout life.
Question 6.
Areolar connective tissue binds muscles with bones.
Question 7.
Cells of cork are dead, suberised and compacdy arranged.
Question 8.
Voluntary muscles control the movement of iris of eye.
Matching Type Questions
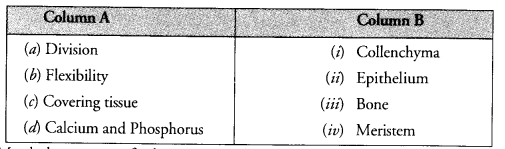
Question 9.
Match the contents of the columns A and B (single matching)
Question 10.
Match the contents of columns I, II and III (Double matching)

Question 11.
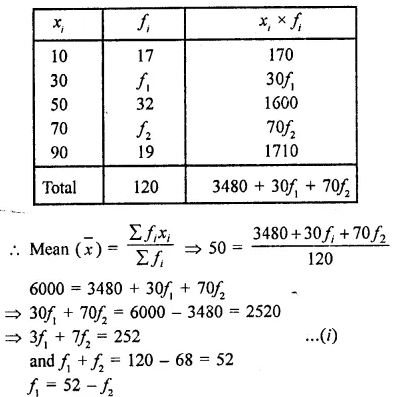
Which one of the following tissues are involved in growth (G), absorption (A), transportation (T) (Key or check list items)
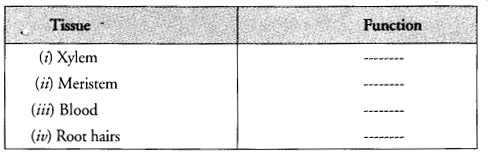
Question 12.
Match the Stimulus with Appropriate Response.

Fill in the Blanks
Question 13. Animals move around in search of ………….. mate and shelter.
Question 14. A thick waterproof coating of ………… occurs over the epidermis in desert plants.
Question 15. ……………. consists of tracheids, vessels, parenchyma and fibres.
Question 16. ………….. epithelium occurs in the lining of renal tubules and ducts of salivary glands.
Question 17. Tendons connect …………….. with bones.
Answers:
SOME ACTIVITY BASED QUESTIONS
Question 1.
Why is blood considered to be connective tissue ?
Answer:
- Like other connective tissues, blood consists of living cells scattered in an abundant matrix. The matrix is liquid or plasma in blood.
- Blood circulates throughout the body, receiving and providing materials to all tissues and organs of the body. It thus connects all parts of the body.
Question 2.
What is aerenchyma ? Give its functions.
Answer:
Definition: It is a specialised parenchyma found in aquatic plants which consists of network of small cells that enclose large air cavities.
Functions:
- Storage of Gases: It stores metabolic gases, O2 and CO2, for use inside the plants in respiration and photosynthesis.
- Buoyancy: It makes the aquatic plant buoyant both inside and over the surface of water.
Question 3.
What is skeletal connective tissue ? Give its functions.
Answer:
Definition: Skeletal connective tissue is that connective tissue in which the matrix is solid and the living cells occur inside fluid filled spaces called lacunae. It is of two types, cartilage and bone.
Functions:
- Endoskeleton: It forms the internal supporting framework of the animal body.
- Protection: The tissue protects the vital organs like brain, spinal cord, heart, lungs, etc.
- Joints: The tissue forms joints which allow for growth and movement of body parts.
- Muscles: It provides surface for attachement to muscles.
- Blood Cells: They develop inside red marrow of bones.
- Minerals: Bony skeleton stores minerals, some of which are withdrawn by the body in case of emergency.
Question 4.
What is synapse ? Explain.
Answer:
It is a junction between two neurons without developing an organic union. The terminal knobbed branch end of an axon of one neuron comes in near contact with a dendrite terminal of the next neuron. A narrow fluid filled space occurs between the two. An activated axon end passes out a neurotransmitter like acetylcholine which provides sensation to dendrite terminal. This helps in transfer of impulse from one neuron to the next.
NCERT Solutions for Class 9 Science Chapter 6 Tissues
Hope given NCERT Solutions for Class 9 Science Chapter 6 are helpful to complete your science homework.
If you have any doubts, please comment below. Learn Insta try to provide online science tutoring for you.