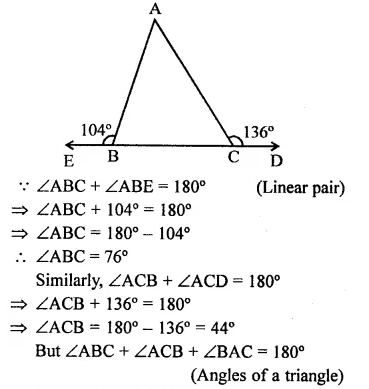
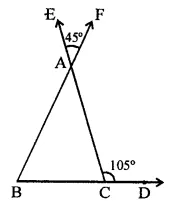
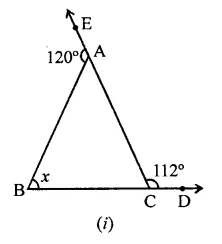
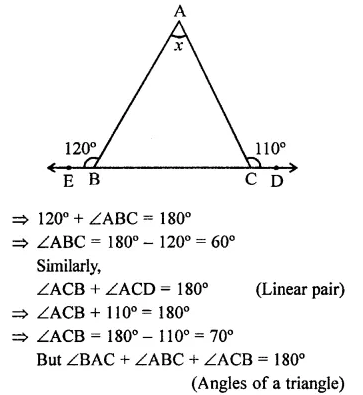
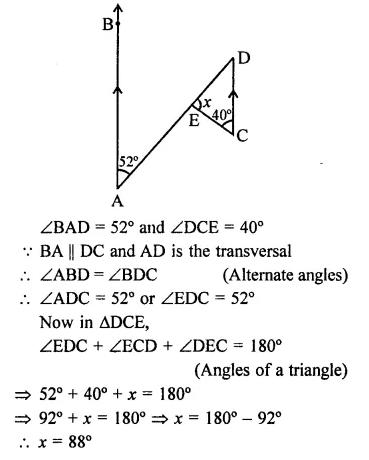
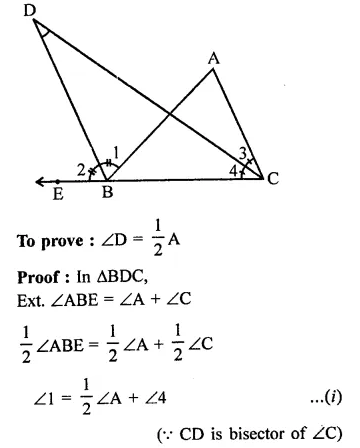
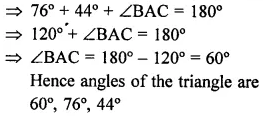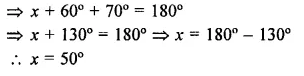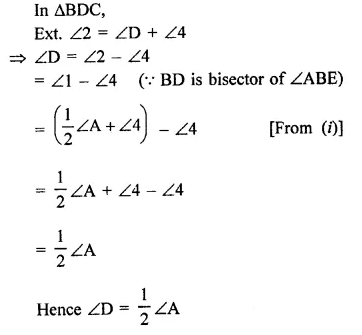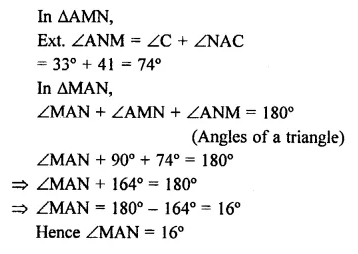CBSE Class 9

CBSE Class 9

Value Based Questions in Science for Class 9 Chapter 6 Tissues

by

Value Based Questions in Science for Class 9 Chapter 6 Tissues

These Solutions are part of Value Based Questions in Science for Class 9. Here we have given Value Based Questions in Science for Class 9 Chapter 6 Tissues

Question 1.
Name four economically important plant fibres derived from sclerenchyma. Why they differ in their softness and durability ?
Answer:
Four fibres : Flax, Hemp, Jute, Coconut. In Coconut, the fibres are obtained from husk (mesocarp) of fruit. In others they are obtained from stems, being bast or phloem fibres.
The fibres differ in their hardness and strength. Hardness is due to excessive deposition of lignin as in Coconut and Jute. Because of it, they are prone to deterioration on wetting. Coconut fibres are used in preparation of mats while Jute fibres are used in preparing sacks. Flax and Hemp yield high quality durable clothing. They have smaller amounts of lignin.

More Resources

Question 2.
What is bark ? Give its importance. Why are certain barks used in medicines ?
Answer:
Bark is the outer protective covering of stems and roots of woody plants. It is mostly made up of cork that consists of several layers of compactly arranged dead rectangular cells. The cells are impermeable due to deposition of suberin. They contain air, tannins, resins and alkaloids.
Importance:

  1. Protection against water loss due to impermeable nature of cell walls.
  2. Protection against microbes due to impervious nature.
  3. Insulation from extremes of temperature, mechanical injury and browsing by animals.
  4. Cork is used commercially in stoppers for bottles, insulation boards, shock absorbers, linoleum and sports goods.
  5. Tannin rich bark is used in dyes.
  6. Inner bark of Cinnamon is a common spice.

Bark in Medicines: 

  1. Quinine is obtained from the bark of Cinchona,
  2. Taxol is got from bark of Taxus. Medicinal barks possess alkaloids.

Question 3.
What is cartilage ? What is its importance to bones ?
Answer:
Cartilage is flexible soft supportive connective tissue having non-vascularised solid matrix of chondrin with fluid filled lacunae containing 1-4 living cells called chondrocytes.
Importance to Bones :

  1. Cartilage occurs over articular surfaces of bones where it protects them from frictional damage during movement against one another.
  2. It lies at sternal ends of ribs to give them flexibility in movement during breathing,
  3. It occurs as intervertebral discs to function as cushions in the vertebral column.

Question 4.
Why are medullated nerve fibres more efficient than non-medullated nerve fibres ?
Answer:
Medullated nerve fibres are those axons which have a covering of fat rich medullary sheath below the neurilemma. They are more efficient than non-medullated nerve fibres due to two reasons.

  1. Being well insulated, the fibres do not meet any interference in impulse conduction from other nearby nerve fibres.
  2. Medullated nerve fibres have nodes of Ranvier. An impulse does not travel all along the axon but jumps from one node of Ranvier to the next. By this saltation medullated nerve fibres are some fifty times (50 X) more efficient in impulse transmission as compared to non-medullated nerve fibres.

Hope given Value Based Questions in Science for Class 9 Chapter 6 Tissues are helpful to complete your science homework.

If you have any doubts, please comment below. Learn Insta try to provide online science tutoring for you.

RD Sharma Class 9 Solutions Chapter 11 Co-ordinate Geometry Ex 11.2

by

RD Sharma Class 9 Solutions Chapter 11 Co-ordinate Geometry Ex 11.2

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 11 Co-ordinate Geometry Ex 11.2

Other Exercises

Question 1.
The exterior angles obtained on producing the base of a triangle both ways are 104° and 136°. Find all the angles of the triangle.
Solution:
In ∆ABC, base BC is produced both ways to D and E respectivley forming ∠ABE = 104° and ∠ACD = 136°
RD Sharma Class 9 Solutions Chapter 11 Co-ordinate Geometry Ex 11.2 Q1.1
RD Sharma Class 9 Solutions Chapter 11 Co-ordinate Geometry Ex 11.2 Q1.2

Question 2.
In the figure, the sides BC, CA and AB of a ∆ABC have been produced to D, E and F respectively. If ∠ACD = 105° and ∠EAF = 45°, find all the angles of the ∆ABC.
RD Sharma Class 9 Solutions Chapter 11 Co-ordinate Geometry Ex 11.2 Q2.1
Solution:
In ∆ABC, sides BC, CA and BA are produced to D, E and F respectively.
∠ACD = 105° and ∠EAF = 45°
∠ACD + ∠ACB = 180° (Linear pair)
⇒ 105° + ∠ACB = 180°
⇒ ∠ACB = 180°- 105° = 75°
∠BAC = ∠EAF (Vertically opposite angles)
= 45°
But ∠BAC + ∠ABC + ∠ACB = 180°
⇒ 45° + ∠ABC + 75° = 180°
⇒ 120° +∠ABC = 180°
⇒ ∠ABC = 180°- 120°
∴ ∠ABC = 60°
Hence ∠ABC = 60°, ∠BCA = 75°
and ∠BAC = 45°

Question 3.
Compute the value of x in each of the following figures:
RD Sharma Class 9 Solutions Chapter 11 Co-ordinate Geometry Ex 11.2 Q3.1

RD Sharma Class 9 Solutions Chapter 11 Co-ordinate Geometry Ex 11.2 Q3.2
RD Sharma Class 9 Solutions Chapter 11 Co-ordinate Geometry Ex 11.2 Q3.3
Solution:
(i) In ∆ABC, sides BC and CA are produced to D and E respectively
RD Sharma Class 9 Solutions Chapter 11 Co-ordinate Geometry Ex 11.2 Q3.4
RD Sharma Class 9 Solutions Chapter 11 Co-ordinate Geometry Ex 11.2 Q3.5
(ii) In ∆ABC, side BC is produced to either side to D and E respectively
∠ABE = 120° and ∠ACD =110°
∵ ∠ABE + ∠ABC = 180° (Linear pair)
RD Sharma Class 9 Solutions Chapter 11 Co-ordinate Geometry Ex 11.2 Q3.6
RD Sharma Class 9 Solutions Chapter 11 Co-ordinate Geometry Ex 11.2 Q3.7

(iii) In the figure, BA || DC
RD Sharma Class 9 Solutions Chapter 11 Co-ordinate Geometry Ex 11.2 Q3.8

Question 4.
In the figure, AC ⊥ CE and ∠A: ∠B : ∠C = 3:2:1, find the value of ∠ECD.
RD Sharma Class 9 Solutions Chapter 11 Co-ordinate Geometry Ex 11.2 Q4.1
Solution:
In ∆ABC, ∠A : ∠B : ∠C = 3 : 2 : 1
BC is produced to D and CE ⊥ AC
∵ ∠A + ∠B + ∠C = 180° (Sum of angles of a triangles)
Let∠A = 3x, then ∠B = 2x and ∠C = x
∴ 3x + 2x + x = 180° ⇒ 6x = 180°
⇒ x = \(\frac { { 180 }^{ \circ } }{ 6 }\)  = 30°
∴ ∠A = 3x = 3 x 30° = 90°
∠B = 2x = 2 x 30° = 60°
∠C = x = 30°
In ∆ABC,
Ext. ∠ACD = ∠A + ∠B
⇒ 90° + ∠ECD = 90° + 60° = 150°
∴ ∠ECD = 150°-90° = 60°

Question 5.
In the figure, AB || DE, find ∠ACD.
RD Sharma Class 9 Solutions Chapter 11 Co-ordinate Geometry Ex 11.2 Q5.1
Solution:
In the figure, AB || DE
AE and BD intersect each other at C ∠BAC = 30° and ∠CDE = 40°
∵ AB || DE
∴ ∠ABC = ∠CDE (Alternate angles)
RD Sharma Class 9 Solutions Chapter 11 Co-ordinate Geometry Ex 11.2 Q5.2
⇒ ∠ABC = 40°
In ∆ABC, BC is produced
Ext. ∠ACD = Int. ∠A + ∠B
= 30° + 40° = 70°

Question 6.
Which of the following statements are true (T) and which are false (F):
(i) Sum of the three angles of a triangle is 180°.
(ii) A triangle can have two right angles.
(iii) All the angles of a triangle can be less than 60°.
(iv) All the angles of a triangle can be greater than 60°.
(v) All the angles of a triangle can be equal to 60°.
(vi) A triangle can have two obtuse angles.
(vii) A triangle can have at most one obtuse angles.
(viii) If one angle of a triangle is obtuse, then it cannot be a right angled triangle.
(ix) An exterior angle of a triangle is less than either of its interior opposite angles.
(x) An exterior angle of a triangle is equal to the sum of the two interior opposite angles.
(xi) An exterior angle of a triangle is greater than the opposite interior angles.
Solution:
(i) True.
(ii) False. A right triangle has only one right angle.
(iii) False. In this, the sum of three angles will be less than 180° which is not true.
(iv) False. In this, the sum of three angles will be more than 180° which is not true.
(v) True. As sum of three angles will be 180° which is true.
(vi) False. A triangle has only one obtuse angle.
(vii) True.
(viii)True.
(ix) False. Exterior angle of a triangle is always greater than its each interior opposite angles.
(x) True.
(xi) True.

Question 7.
Fill in the blanks to make the following statements true:
(i) Sum of the angles of a triangle is ………
(ii) An exterior angle of a triangle is equal to the two …….. opposite angles.
(iii) An exterior angle of a triangle is always …….. than either of the interior opposite angles.
(iv) A triangle cannot have more than ………. right angles.
(v) A triangles cannot have more than ……… obtuse angles.
Solution:
(i) Sum of the angles of a triangle is 180°.
(ii) An exterior angle of a triangle is equal to the two interior opposite angles.
(iii) An exterior angle of a triangle is always greater than either of the interior opposite angles.
(iv) A triangle cannot have more than one right angles.
(v) A triangles cannot have more than one obtuse angles.

Question 8.
In a ∆ABC, the internal bisectors of ∠B and ∠C meet at P and the external bisectors of ∠B and ∠C meet at Q. Prove that ∠BPC + ∠BQC = 180°.
Solution:
Given : In ∆ABC, sides AB and AC are produced to D and E respectively. Bisectors of interior ∠B and ∠C meet at P and bisectors of exterior angles B and C meet at Q.
RD Sharma Class 9 Solutions Chapter 11 Co-ordinate Geometry Ex 11.2 Q8.1
To prove : ∠BPC + ∠BQC = 180°
Proof : ∵ PB and PC are the internal bisectors of ∠B and ∠C
∠BPC = 90°+ \(\frac { 1 }{ 2 }\) ∠A …(i)
Similarly, QB and QC are the bisectors of exterior angles B and C
∴ ∠BQC = 90° + \(\frac { 1 }{ 2 }\) ∠A …(ii)
Adding (i) and (ii),
∠BPC + ∠BQC = 90° + \(\frac { 1 }{ 2 }\) ∠A + 90° – \(\frac { 1 }{ 2 }\) ∠A
= 90° + 90° = 180°
Hence ∠BPC + ∠BQC = 180°

Question 9.
In the figure, compute the value of x.
RD Sharma Class 9 Solutions Chapter 11 Co-ordinate Geometry Ex 11.2 Q9.1
Solution:
In the figure,
∠ABC = 45°, ∠BAD = 35° and ∠BCD = 50° Join BD and produce it E
RD Sharma Class 9 Solutions Chapter 11 Co-ordinate Geometry Ex 11.2 Q9.2

Question 10.
In the figure, AB divides ∠D AC in the ratio 1 : 3 and AB = DB. Determine the value of x.
RD Sharma Class 9 Solutions Chapter 11 Co-ordinate Geometry Ex 11.2 Q10.1
Solution:
In the figure AB = DB
RD Sharma Class 9 Solutions Chapter 11 Co-ordinate Geometry Ex 11.2 Q10.2
RD Sharma Class 9 Solutions Chapter 11 Co-ordinate Geometry Ex 11.2 Q10.3

Question 11.
ABC is a triangle. The bisector of the exterior angle at B and the bisector of ∠C intersect each other at D. Prove that ∠D = \(\frac { 1 }{ 2 }\) ∠A.
Solution:
Given : In ∠ABC, CB is produced to E bisectors of ext. ∠ABE and into ∠ACB meet at D.
RD Sharma Class 9 Solutions Chapter 11 Co-ordinate Geometry Ex 11.2 Q11.1
RD Sharma Class 9 Solutions Chapter 11 Co-ordinate Geometry Ex 11.2 Q11.2

Question 12.
In the figure, AM ⊥ BC and AN is the bisector of ∠A. If ∠B = 65° and ∠C = 33°, find ∠MAN.
RD Sharma Class 9 Solutions Chapter 11 Co-ordinate Geometry Ex 11.2 Q12.1
Solution:
RD Sharma Class 9 Solutions Chapter 11 Co-ordinate Geometry Ex 11.2 Q12.2
RD Sharma Class 9 Solutions Chapter 11 Co-ordinate Geometry Ex 11.2 Q12.3

Question 13.
In a AABC, AD bisects ∠A and ∠C > ∠B. Prove that ∠ADB > ∠ADC.
Solution:
Given : In ∆ABC,
∠C > ∠B and AD is the bisector of ∠A
RD Sharma Class 9 Solutions Chapter 11 Co-ordinate Geometry Ex 11.2 Q13.1
To prove : ∠ADB > ∠ADC
Proof: In ∆ABC, AD is the bisector of ∠A
∴ ∠1 = ∠2
In ∆ADC,
Ext. ∠ADB = ∠l+ ∠C
⇒ ∠C = ∠ADB – ∠1 …(i)
Similarly, in ∆ABD,
Ext. ∠ADC = ∠2 + ∠B
⇒ ∠B = ∠ADC – ∠2 …(ii)
From (i) and (ii)
∵ ∠C > ∠B (Given)
∴ (∠ADB – ∠1) > (∠ADC – ∠2)
But ∠1 = ∠2
∴ ∠ADB > ∠ADC

Question 14.
In ∆ABC, BD ⊥ AC and CE ⊥ AB. If BD and CE intersect at O, prove that ∠BOC = 180°-∠A.
Solution:
Given : In ∆ABC, BD ⊥ AC and CE⊥ AB BD and CE intersect each other at O
RD Sharma Class 9 Solutions Chapter 11 Co-ordinate Geometry Ex 11.2 Q14.1
To prove : ∠BOC = 180° – ∠A
Proof: In quadrilateral ADOE
∠A + ∠D + ∠DOE + ∠E = 360° (Sum of angles of quadrilateral)
⇒ ∠A + 90° + ∠DOE + 90° = 360°
∠A + ∠DOE = 360° – 90° – 90° = 180°
But ∠BOC = ∠DOE (Vertically opposite angles)
⇒ ∠A + ∠BOC = 180°
∴ ∠BOC = 180° – ∠A

Question 15.
In the figure, AE bisects ∠CAD and ∠B = ∠C. Prove that AE || BC.
RD Sharma Class 9 Solutions Chapter 11 Co-ordinate Geometry Ex 11.2 Q15.1
Solution:
Given : In AABC, BA is produced and AE is the bisector of ∠CAD
∠B = ∠C
RD Sharma Class 9 Solutions Chapter 11 Co-ordinate Geometry Ex 11.2 Q15.2
To prove : AE || BC
Proof: In ∆ABC, BA is produced
∴ Ext. ∠CAD = ∠B + ∠C
⇒ 2∠EAC = ∠C + ∠C (∵ AE is the bisector of ∠CAE) (∵ ∠B = ∠C)
⇒ 2∠EAC = 2∠C
⇒ ∠EAC = ∠C
But there are alternate angles
∴ AE || BC

Hope given RD Sharma Class 9 Solutions Chapter 11 Co-ordinate Geometry Ex 11.2 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

HOTS Questions for Class 9 Science Chapter 6 Tissues

by

HOTS Questions for Class 9 Science Chapter 6 Tissues

These Solutions are part of HOTS Questions for Class 9 Science. Here we have given HOTS Questions for Class 9 Science Chapter 6 Tissues

Question 1.
What will happen if

  1. Apical meristem is damaged or cut ?
  2. Cork is not formed in older stems and roots ?
  3. Cells of epithelial tissue are not compactly packed.
  4. Lymph is not returned to blood ?

Answer.

  1. Apical Meristem Removed: Growth in length will stop.
  2. Cork is Not Formed: If cork is not formed in older stems and roots, the outer tissues will rupture with the increase in girth and expose the interior to desiccation and infection.
  3. Epithelial tissue will not be effective as protective impermeable layer.
  4. Lymph is Not Returned to Blood: Blood volume will decrease while passage of materials from tissues to blood and vice versa would be dislocated.

More Resources

Question 2.

  1. Identify figures : A,B and C.
    HOTS Questions for Class 9 Science Chapter 6 Tissues image - 1
  2. Which one of them provides both mechanical strength as well as flexibility ?
  3. Which one of them is commercially exploited to obtain Hemp and Jute ?
  4. Which one of them can be modified to form air cavities in aquatic plants ?
  5. Which one of them has heavy deposition of lignin ?

Answer:

  1. A- T.S sclerenchyma fibres.
    B- T.S parenchyma cells.
    C- T. S collenchyma.
  2. Mechanical strength and flexibility: Collenchyma.
  3. Hemp and Jute: Sclerenchyma fibres.
  4. Aerenchyma: Modification of parenchyma.
  5. Deposition of Lignin: Sclerenchyma.

Question 3.

  1. Identify the figure. What is its function ?
    HOTS Questions for Class 9 Science Chapter 6 Tissues image - 2
  2. Label X, Y and Z .
  3. Which ones of them develop from the same mother cell ?
  4. X loses its nucleus in mature state. Still it remains alive. How ?

Answer:

  1. Identification: Phloem tissue.
    Function: Conduction of organic food.
  2. X – Sieve tube cell.
    Y – Sieve plate
    Z – Companion cell.
  3. From Same Mother Cell: Sieve tube cell and companion cell.
  4. Living of Sieve Tube Cells: It is controlled by nucleated companion cells with which they are connected by plasmodesmata.

Question 4.

  1. Identify figures A and B.
    HOTS Questions for Class 9 Science Chapter 6 Tissues image - 3
  2. Which is called tesselated and pavement epithelium ?
  3. Which one lines gastro-intestinal tract and epiglottis ?
  4. Which one allows diffusion of substances ?

Answer:

  1. Identification:
    A- Squamous epithelium
    B- Ciliated columnar epithelium.
  2. Pavement Epithelium: Squamous epithelium.
    Tesselated Epithelium: Squamous epithelium.
  3. Gastro-intesinal Tract: Simple columnar epithelium.
    Epiglottis: Stratified columnar epithelium.
  4. Diffusion of Substances: Simple epithelium, especially squamous one.

Question 5.

  1. Identify the figure.
    HOTS Questions for Class 9 Science Chapter 6 Tissues image - 4
  2. Label X, Y and Z.
  3. What is the chemical composition of material of the figure ?
  4. What is the function of Y

Answer:

  1. Identification: Section of bone.
  2. X- Periosteum.
    Y- Haversian canal
    Z- Canaliculus (plural canaliculi)
  3. Composition,
    1. Ossein (30-40%)
    2. Mineral matter
      (60-70%) of calcium and magnesium carbonate and phosphate.
  4. Function of Haversian Canal: To carry nutrients to the interior of the bone.

Question 6.
What will happen if

  1. Bone is dipped in HCl
  2. Bone is dried ?

Answer:

  1. Bone Dipped in HCl. Mineral matter dissolves. Only organic matter is left.
  2. Dried Bone. Organic matter destroyed. Only mineral matter is left.

Question 7.
What will happen if

  1. Ligament gets overstretched ?
  2. Heparin is absent in blood ?
  3. Striated muscles contract rapidly for longer duration ?

Answer:

  1. Oversretching of Ligament: Sprain.
  2. Absence of Heparin in Blood: Blood coagulation occurs inside the blood vessels.
  3. Striated Muscle Contraction: Fatigue due to accumulation of lactic acid.

Question 8.

  1. Identify figures A and B .
    HOTS Questions for Class 9 Science Chapter 6 Tissues image - 5
  2. Label X, Y and Z.
  3. Which one acts as impulse booster ?
  4. Which one is under control of our will ?

Answer:

  1. Identification:
    A – Cardiac muscle fibres.
    B – Striated muscle fibre.
  2. X- Intercalated disc.
    Y- Dark band.
    Z- Light band.
  3. Impulse Booster: Intercalated disc.
  4. Control of Will: Striated or skeletal muscle.

Hope given HOTS Questions for Class 9 Science Chapter 6 Tissues are helpful to complete your science homework.

If you have any doubts, please comment below. Learn Insta try to provide online science tutoring for you.

RD Sharma Class 9 Solutions Chapter 24 Measures of Central Tendency VSAQS

by

RD Sharma Class 9 Solutions Chapter 24 Measures of Central Tendency VSAQS

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 24 Measures of Central Tendency VSAQS

Other Exercises

Question 1.
If the ratio of mode and median of a certain data is 6 : 5, then find the ratio of its mean and median.
Solution:
We know that
Mode = 3 median – 2 mean…(i)
and \(\frac { mode }{ median } \) = \(\frac { 6 }{ 5 } \)
Mode = \(\frac { 6 }{ 5 } \)median
∴From (i), \(\frac { 6 }{ 5 } \) median = 3 median – 2 mean
=> 2 mean = 3 median – \(\frac { 6 }{ 5 } \)median
2 mean = \(\frac { 15-6 }{ 5 } \)median = \(\frac { 9 }{ 5 } \)median
\(\frac { mean }{ median } \) = \(\frac { 9 }{ 5X2 } \) = \(\frac { 9 }{ 10 } \)
∴Ratio = 9:10

Question 2.
If the mean of x + 2, 2x + 3, 3x + 4, 4x + 5 is x + 2, find x.
Solution:
Mean of x + 2, 2x + 3, 3x + 4, 4x + 5 = x + 2
=> \(\frac { x + 2+2x + 3+3x + 4+4x + 5 }{ 4 } \) = x + 2
=> 10x + 14 = 4x + 8
=> 10x – 4x = 8 – 14
=> 6x= – 6
∴ x = – 1

Question 3.
If the median of scores ,\(\frac { x }{ 2 } \), \(\frac { x }{ 3 } \), \(\frac { x }{ 4 } \), \(\frac { x }{ 5} \) and \(\frac { x }{ 6 } \) (where x > 0) is 6, then find the value \(\frac { x }{ 6 } \)
Solution:
\(\frac { x }{ 2 } \), \(\frac { x }{ 3 } \), \(\frac { x }{ 4 } \), \(\frac { x }{ 5} \), \(\frac { x }{ 6 } \)
Here n = 5
Median = \(\frac { n+1 }{ 2 } \) th term = \(\frac { 5+1 }{ 2 } \) th
\(\frac { 6 }{ 2 } \) = 3rd term = \(\frac { x }{ 4 } \)
\(\frac { x }{ 4 } \) = 6 => x = 24
\(\frac { x }{ 6 } \) = \(\frac { 24 }{ 6 } \) = 4
∴Hence = \(\frac { x }{ 6 } \) = 4

Question 4.
If the mean of 2, 4, 6, 8, x, y is 5, then find the value of x + y.
Solution:
Mean of 2, 4, 6, 8, x, y is 5
\(\frac { 2+4+6+8+x+y }{ 6 } \) = 5
\(\frac { 20+x+y }{ 6 } \) = 5
=> 20 + (x +y) = 30
=> x + y = 30 – 20 = 10
∴x + y = 10

Question 5.
If the mode of scores 3, 4, 3, 5, 4, 6, 6, x is 4, find the value of x.
Solution:
Mode of 3, 4, 3, 5, 4, 6, 6, x is 4
∴ 4 comes in maximum times
But here ,
3 2
4 2
5 1
6 2
3, 4 and 6 are equal in number
∴ x must be 4 so that it becomes in maximum times

Question 6.
If the median of 33, 28, 20. 25, 34, x is 29. find the maximum possible value of x.
Solution:
Median of 33, 28, 20, 25, 34, x is 29
Now arranging in ascending order 20, 25, 28, x, 33, 34
Here n = 6
Median = \(\frac { 1 }{ 2 } \left[ \frac { 6 }{ 2 } th\quad term+\left( \frac { 6 }{ 2 } +1 \right) th\quad term \right] \)
29 = \(\frac { 1 }{ 2 } \) [3rd term + 4th term]
29 = \(\frac { 1 }{ 2 } \) [28+x]
58 = 28 + x
=> x = 58 – 28 = 30
∴Possible value of x = 30

Question 7.
If the median of the scores 1, 2, x, 4, 5 (where 1 <2 <x <4 <5) is 3, then find the mean of the scores.
Solution:
Scores are 1, 2, x, 4, 5 and median 3
Here n = 5 which is odd
Median = \(\frac { n+1 }{ 2 } \) th term = \(\frac { 5+1 }{ 2 } \) = \(\frac { 6 }{ 2 } \) th
=> 3 = 3rd term = x
=> 3 = x
∴ x = 3
Mean of the score = \(\frac { 1+2+3+4+5 }{ 5 } \) = 3

Question 8.
If the ratio of mean and median of a certain data is 2 : 3, then find the ratio of its mode and mean.
Solution:
We know that mode = 3 median – 2 mean
RD Sharma Class 9 Solutions Chapter 24 Measures of Central Tendency VSAQS 8.1
\(\frac { mode }{ mean } \) = \(\frac { 5 }{ 2 } \)
Ratio in mode and mean = 5 : 2

Question 9.
The arithmetic mean and mode of a data are 24 and 12 respectively, then find the median of the data.
Solution:
Mean = 24
Mode = 12
We know that mode = 3 median – 2 mean
12 = 3 median – 2 x 24
12 = 3 median – 48
3 median 12 + 48 = 60
Median = \(\frac { 60 }{ 3 } \) = 20

Question 10.
If the difference of mode and median of a data is 24, then find the difference of median and mean.
Solution:
Mode – Median = 24
Mode = 24 + median
But mode = 3 median – 2 mean
3 median – 2 mean = 24 + median
3 median – median – 2 mean = 24
=> 2 median – 2 mean = 24
=> Median – Mean = 12 (Dividing by 2)

Hope given RD Sharma Class 9 Solutions Chapter 24 Measures of Central Tendency VSAQS are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 9 Solutions Chapter 24 Measures of Central Tendency Ex 24.4

by

RD Sharma Class 9 Solutions Chapter 24 Measures of Central Tendency Ex 24.4

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 24 Measures of Central Tendency Ex 24.4

Other Exercises

Question 1.
Find out the mode of the following marks obtained by 15 students in a class:
Marks : 4, 6, 5, 7, 9, 8, 10, 4, 7, 6, 5, 9, 8, 7, 7.
Solution:
Marks obtained are in ascending order,
4, 4, 5, 5, 6, 6, 7, 7, 7, 7, 8, 8, 9, 9, 10
Here we see that 7 is the number which is maximum times i.e. 4 times
Mode = 7

Question 2.
Find the mode for the following data:
125, 175, 225, 125, 225, 175, 325, 125, 375, 225, 125
Solution:
Arranging in ascending order,
125, 125, 125, 125, 175, 175, 225, 225, 225, 325, 375
We see that, 125 is the number which is in maximum times
Mode = 125

Question 3.
Find the mode for the following series:
7.5, 7.3, 7.2, 7.2, 7.4, 7.7, 7.7, 7.5, 7.3, 7.2, 7.6, 7.2
Solution:
Arranging in ascending order,
7.2, 7.2, 7.2, 7.2, 7.3, 7.3, 7.4, 7.5, 7.5, 7.6, 7.7, 7.7
We see that 7.2 comes in maximum times
Mode = 7.2

Question 4.
Find the mode of the following data in each case:
(i) 14, 25, 14, 28, 18, 17, 18, 14, 23, 22, 14, 18
(ii) 7, 9, 12, 13, 7, 12, 15, 7, 12, 7, 25, 18, 7
Solution:
(i) 14, 25, 14, 28, 18, 17, 18, 14, 23, 22, 14, 18
Arranging in ascending order,
14, 14, 14,. 14, 17, 18, 18, 18, 22, 23, 25, 28
Here we see that 14 comes in maximum times
Mode = 14
(ii) 7, 9, 12, 13, 7, 12, 15, 7, 12, 7, 25, 18, 7
Arranging in order,
7, 7, 7, 7, 7, 9, 12, 12, 12, 13, 15, 18, 25
Here we see that 7 comes in maximum times
Mode = 7

Question 5.
The demand of different shirt sizes, as obtained by a survey, is given below:
RD Sharma Class 9 Solutions Chapter 24 Measures of Central Tendency Ex 24.4 5.1
Find the modal shirt sizes, as observed from the survey.
Solution:
From the given data
RD Sharma Class 9 Solutions Chapter 24 Measures of Central Tendency Ex 24.4 5.2
From above, we see that
Modal size is 39 as it has maximum times persons

Hope given RD Sharma Class 9 Solutions Chapter 24 Measures of Central Tendency Ex 24.4 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.