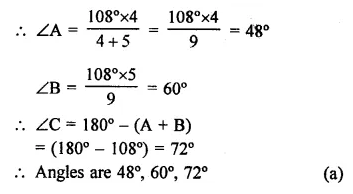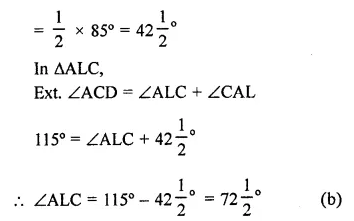CBSE Class 9

NCERT Exemplar Solutions for Class 9 Science Chapter 15 Improvement in Food Resources

These Solutions are part of NCERT Exemplar Solutions for Class 9 Science . Here we have given NCERT Exemplar Solutions for Class 9 Science Chapter 15 Improvement in Food Resources

Question 1.
Match the items of column A with those of column B.

Answer:
a — ii,
b — iii,
c — i,
d — iv.

More Resources

• NCERT Exemplar Solutions for Class 9 Science
• NCERT Solutions for Class 9 Science
• Value Based Questions in Science for Class 9
• HOTS Questions for Class 9 Science
• Previous Year Question Papers for CBSE Class 9 Science

Question 2.
Fill in the blanks
(a) Pigeon Pea is a good source of ………… .
(b) Berseem is an important …………. crop.
(c) The crops which are grown in rainy season are called ………….. crops.
(d) ………… are rich in vitamins.
(e) ………… crop grows in winter seasons.
Answer:
(a) protein
(b) fodder
(c) kharif
(d) Vegetables
(e) Rabi.

Question 3.
What is GM crop ? Name any one crop which is grown in India.
Answer:
GM or genetically modified crop is the one which has been developed through introduction of some specific genes from other sources, e.g, insect resistant B Cotton (being grown in India), vitamin A rich Golden Rice.

Question 4.
List out some useful traits in improved crop.
Answer:

1. Higher yield
2. Improved quality
3. Resistance to biotic and abiotic stresses
4. Change in maturity
5. Wider adaptability
6. Desirable agronomic traits.

Question 5.
Why is organic matter important for crop production ?
Answer:
Organic matter forms humus. It is important for crop production because it makes the soil fertile.

1. Organic matter improves soil structure by forming soil crumbs.
2. It increases water holding capacity of sandy soils.
3. It improves aeration of clayey soils.
4. During its decomposition, it liberates minerals which enrich the soil.
5. Biochemicals present in decaying organic matter improve growth of crop plants.

Question 6.
Why is use of excess fertilizer detrimental for environment ?
Answer:
Use of excess fertilisers will cause :

1. Mineral loading of underground water.
2. Excess minerals in the crop plants.
3. Salination of soil.
4. Run off from fertilizers rich soil, will cause eutrophication of water bodies.

Question 7.
Give one word for the following :
(a) Farming without the use of chemicals as fertilizers, herbicides and pesticides is known as ……….. .
(b) Growing of Wheat and Groundnut on the same field is called ………… .
(c) Planting of Soyabean and Maize in alternate rows in the same field is called as ………… .
(d) Growing different crops on a piece of land in pre-planned succession is known as ………….. .
(e) Xanthium and Parthenium are commonly known as …………. .
(f) Causal organism of any disease is called as …………. .
Answer:
(a) Organic farming
(b) mixed cropping
(c) Inter-cropping
(d) crop rotation
(e) weeds
(f) pathogen.

Question 8.
Match the columns A and B.

Answer:
a — iii,
b — v,
c — iv,
d — i,
e — ii.

Question 9.
If there is low rainfall in a village throughout the year, what measures will you suggest to the farmers for better cropping.
Answer:

1. Reduced tilling
2. Enrich soil with humus which increases its water holding capacity
3. Use of drought resistant and early maturing varieties of crops.

Question 10.
Group the following and tabulate them as energy yielding, protein yielding, oil yielding and fodder crop :
Wheat, Rice, Berseem, Maize, Gram, Oat, Pigeon Gram, Sudan Grass, Lentil, Soyabean, Groundnut, Castor and Mustard.
Answer:

1. Wheat, Rice, Maize, Oat Energy yielding.
2. Gram, Pigeon Gram, Lentil, Soyabean Protein yielding.
3. Ground nut, Castor, Mustard, Soyabean Oil yeilding.
4. Berseem, Oat, Sudan Grass Fodder crops.

Question 11.
Define the terms hybridisation and photoperiod.
Answer:
Hybridisation. It is crossing of two (or more) types of individuals with different useful traits in order to bring them together in the progeny.
Photoperiod. It is duration of day light that influences plants and other organisms in their growth, reproduction and maturation.

Question 12.
Fill in the blanks :
(a) Photoperiod affect the …………. .
(b) Kharif crops are cultivated from ……….. to ……….. .
(c) Rabi crops are cultivated from ………… to ……….. .
(d) Paddy, Maize, Green Gram and Black Gram are ……….. crops.
(e) Wheat, Gram, Pea and Mustard are …………. crops.
Answer:
(a) flowering (of plants)
(b) June, October
(c) November, April
(d) kharif
(e) rabi.

Question 13.
Cultivation practices and crop yield are related to environmental conditions. Explain.
Answer:
All crops do not grow under similar conditions. Some require high temperature, some low temperature, longer duration of sunlight, shorter duration of sunlight, more humidity, low humidity, moderate humidity, loam soil, sandy soil, etc. Apple cannot be grown in plains because it requires several days of low temperature. In plains, there are two major seasons of crop
plants kharif (rainy season) and rabi (winter season).

Question 14.
Fill in the blanks :
(a) A total of …………. nutrients are essential to plants.
(b) ……… and ………. are supplied by air to plants.
(c) ………. is supplied by water to plants.
(d) Soil supplies ………. nutrients to plants.
(e) ……….. nutrients are required in large quantity and called as
(f) ……….. nutrients are needed in small quantity for plants and are called ………… .
Answer:
(a) 16
(b) Carbon, oxygen
(c) Hydrogen
(d) 13
(e) six, macronutrients
(f) seven, micronutrients.

Question 15.
Differentiate between compost and vermicompost.
Answer:

Question 16.
Arrange these statements in correct sequence of preparation of green manure.
(a) Green plants are decomposed in soil.
(b) Green plants are cultivated for preparing manure or crop plant parts are used.
(c) Plants are ploughed and mixed in soil.
(d) After decomposition, it becomes green manure.
Answer:
(b) > (c) > (a) > (d).

Question 17.
An Italian bee variety A melliftra has been introduced in India for honey production. Write about its merits over other varieties.
Answer:
There are three common species of honey bees in our country used for commercial production of honey. These are

1. Apis cerana indica — Indian Bee
2. Apis dorsata — Rock Bee
3. Apis florae {A. florea) — Little Bee

To produce honey at commercial level, the Italian variety of honey bee {Apis mellifera) is commonly used. This variety is domesticated in our country. It is preferred because

1. It is gentle in nature
2. It has good honey collection capacity
3. It has the ability to protect itself from enemies and
4. Less swarming.

Question 18.
In agricultural practices, higher input gives higher yield. Discuss how ?
Answer:
In agriculture, higher yield can be obtained only by employing higher yielding varieties, improved farming practices, modern technology, latest agricultural machines and implements, nutrient supply, etc. All these require high cost and knowledge of new techniques and improvements. Therefore, a farmer’s purchasing capacity for inputs determines the cropping system and production practices.

Question 19.
Discuss the role of hybridisation in crop improvement.
Answer:

1. Choice of Parents: Two older varieities of crop having different desirable characteristics, are selected. For example, if we want to obtain a variety having higher yield as well as disease resistance, we should select two existing varieties of crops, one having higher yield and the other having more resistance to diseases.
2. Cross-breeding: The Two Parents. Pollen grains of plants of one variety are dusted over the stigmas of plants of the other variety and vice-versa. It produces a new variety which has good chacateristics of both the parents. The process of crossing plants of two varieties having different traits to produce a hybrid having good traits of both is called The crossing may be intervarietal (between different varieties), intergeneric (between different genera) or interspecific (between different species of the same genus). The most common type of breeding is intervarietal.

Question 20.
Define

1. Vermicompost
2. Green Manure
3. Biofertilizers.

Answer:

1. Vermicompost: It is a manure rich in pulverised organic matter and worm castings. Vermicompost is formed by the activity of earth worms on organic remains.
2. Green Manure: It is manure formed inside soil from young green crop plants ploughed hack into soil. The green manure crops are generally quick growing legume crops which are mulched by ploughing them back into field in tender stage (about 6 — 8 weeks) only, generally at the time of flowering. These crops are completely decomposed in about 1—2 months when the next crop can be sown.
3. Biofertilizers: Living organisms like nitrogen fixing bacteria, nitrogen fixing blue-green algae and mineral solubilising bacteria that supply nutrients to crop plants are called biofertilizers.

Question 21.
Discuss various methods of weed control.
Answer:
Mechanical Methods :

1. Removal of weeds by pulling them out with hand.
2. Removal of weeds by using trowel (khurpa).
3. Removal of weeds by ploughing, burning and flooding before sowing.
4. Removal of weeds by interculture.

Cultural Methods :

1. Timely sowing of crops.
2. Proper seed bed preparation
3. Intercropping
4. Crop rotation

Chemical Methods :
Destroying the weeds by spraying special chemicals called weedicides like, 2, 4—D (2, 4-dichlorophenoxy acetic acid), Butachlor, Atrazine, isoproturon, etc.
Biological Methods :
In the biological control of weeds, some appropriate insects or some other organisms are deliberately put into the crop field having weeds. The insects or other organisms selectively destroy the weed plants but do not harm the crop plants. For example, Cochineal insects are used to eradicate the weed called Opuntia. Mexican Beetle and Cassia can check the growth of Parthenium. Aquatic weeds are controlled by the fish called grass carp.

Question 22.
Differentiate between the following :
(i) Capture fishery and culture fishery (CCE 2011, 2012)
(ii) Mixed cropping and inter cropping
(iii) Bee keeping and poultry farming.
Answer:
(i) Differences between Capture Fishery and Culture Fishery

(ii) Differences between Mixed Cropping and Intercropping. 

(iii) Differences between Bee Keeping and Poultry Farming

Question 23.
Give merits and demerits of fish culture.
Answer:
Merits:

1. Desired Fish: Economically important desired fishes are made available.
2. Smaller Area: A large number of fishes are raised in a small area.
3. Fish Seeding: Fishes are made to breed in different seasons.
4. Mortality: There is little mortality in the younger stages of the fishes.
5. Improvement: Through selective hybridisation, yield and quality of fishes are improved.

Demerits:

1. Genetic Loss: Only some selected high yielding and economically important breeds are reared. Other breeds and varieties are lost.
2. Threat to Biodiversity: Other forms of aquatic organisms are being ignored. Even natural waters are being seeded with economically important fishes so that natural biodiversity has come under threat.

Question 24.
What do you understand by composite fish culture ?
Answer:
Composite culture is highly advantageous:

1. These fishes do not compete with one another for food because they have different types of food habits.
2. The food available in all the zones (parts) of the pond is utilized due to their food habits.
3. The carps consume only natural foods.
4. Six different types of fish are reared in the same pond.
5. The yield is very high.

Question 25.
Why bee keeping should be done in good pasturage ?
Answer:
Pasturage/Crop/Flora: Quality, taste and quantity of honey depend upon the flora or pasturage available for nectar and pollen collection. Pasturage is different in different geographical regions and locations, plains and mountains. The best honey is almond honey of Kashmir.

Question 26.
Write the modes by which insects affect the crop yield.
Answer:
The important types of crops are :

1. Cereal Crops (Grain Crops): Wheat, rice, maize, (major cereals), barley, sorghum, minor millets (minor cereals). They are rich source of carbohydrates that meet the energy requirement of body. Other useful ingredients are dietary fibres, proteins, vitamins and minerals.
2. Pulses (Legume Seeds): Gram (chana), pea (matar), black gram (urad), green gram (moong), pigeon pea (arhar), lentil (masoor). Pulses are rich in proteins.
3. Oil Seed Crops: Groundnut (peanut), mustard, linseed, sunflower, sesame, soyabean, niger, castor[1]. They are a source of oils, fats and fatty acids.                                                                                                 .
4. Fruit and Vegetable Crops: Orange, apple, mango, banana, pineapple, cabbage, cauliflower, brinjal, okra, carrot, beans, potato. They are a source of minerals, vitamins, roughage and small quantities of protein, carbohydrates and oil.
5. Chilly, black pepper, ginger, turmeric. They are used for enhancing palatability of foods.
6. Other Crops: Crop plants also yield fibres (e.g., cotton), sugar (e.g., sugarcane, sugar beet), tobacco, tea, etc.
7. Fodder Crops: Berseem, oat, Sudan grass, sorghum. They provide green fodder to cattle.
8. Castor oil is not edible oil. It is mainly used as a lubricant, purgative, phenyls, hair fixers, etc.

Question 27.
Discuss why pesticides are used in very accurate concentration and in very appropriate manner ?
Answer:
Pesticides should not be used indiscriminately. Only very accurate dose should be applied at appropriate time. Even slight excess of the pesticide is extremely harmful.

1. Pesticides are harmful to soil biota. Therefore, they reduce soil fertility.
2. They pass into ground water and make it toxic.
3. They enter the crop plants and make them toxic.
4. Pesticides pass into surface water through run off from sprayed fields and harm the aquatic biota.

Question 28.
Name two types of animal feed and write their functions.
Answer:

1. The sick animal looks tired. It becomes inactive and tries to remain isolated.
2. There is little interest in taking food.
3. The animal moves slowly, limping well behind others in the herd.
4. The milk yield, egg laying capacity or working capacity of the animal is reduced drastically.
5. The animal passes loose or watery dung.
6. Urine may become coloured.
7. Eyes may turn red.
8. Ears may droop.
9. There may be wheezy breathing, coughing or sneezing.
10. Excessive salivation.
11. Watery nose.
12. The animal may run temperature and shiver.

Question 29.
What would happen if poultry birds are larger in size and have no summer adaptation capacity ? In order to get small sized poultry birds having summer adaptability, what methods will be employed ?
Answer:
Larger sized birds require more feed. Summer adaptation is connected with egg laying. Little summer adaptation reduces egg laying. In order to obtain small sized poultry birds having summer adaptability, it is desirable to

1. Either introduce the required exotic birds from outside and
2. cross breed the local birds with exotic birds from outside. Small sized birds are preferred for
   1. Lower requirement of feed
   2. Higher egg laying capacity
   3. Lower requirement for space.

Question 30.
Suggest some preventive measures for the diseases of poultry birds.
Answer:

1. The poultry birds should be kept in good spacious, airy and ventilated shelter.
2. The shelter should be cleaned properly and regularly. Quick and hygienic disposal of excreta should be ensured.
3. External parasites should be controlled, preferably by applying dilute insecticide solution. Disinfectant should be sprayed to kill mosquitoes and other external parasites.
4. Every animal should be vaccinated to immunise it against common infections and diseases.

Question 31.
The figure shows two crop fields (plots A and B) have been treated by manures and chemical fertilizers respectively, keeping other environmental factors same.

Observe the graph and answer the following questions :

1. Why does plot B show sudden increase and then gradual decrease in yield ?
2. Why is the highest peak in plot A graph slightly delayed ?
3. What is the reason for the different pattern of the two graphs.

Answer:

1. Sudden Increase: Chemical fertilizer supplies the minerals immediately in good quantity. Gradual Decrease. It is due to depletion of nutrients caused by absorption by plants, leaching to lower layers of the soil and killing of decomposer microbes.
2. Manures decay slowly so that release of minerals is also delayed. Manures take time to mix up with the soil and form crumbs, that increase water holding and aeration of the soil.
3. The difference in the two graphs indicates that manuring the soil is more beneficial than the use of chemical fertilizers. Rather, use of chemical fertilizers is harmful in the longer run.

Hope given NCERT Exemplar Solutions for Class 9 Science Chapter 15 Improvement in Food Resources are helpful to complete your science homework.

If you have any doubts, please comment below. Learn Insta try to provide online science tutoring for you.

Value Based Questions in Science for Class 9 Chapter 15 Improvement in Food Resources

These Solutions are part of Value Based Questions in Science for Class 9. Here we have given Value Based Questions in Science for Class 9 Chapter 15 Improvement in Food Resources

Question 1.
Shyam has been cultivating wheat crop year after year in the same field. Recendy he has observed decline in the yield despite best inputs. Agriculture inspector of the area suggested him to sow soyabean for one or two years before again using the field for wheat crop. What is the rationale behind this suggestion ?
Answer:
Sowing the same crop in the same field year after year results in depletion of nutrients from the particular depth of the soil, growing and multiplication of soil borne pathogens and pests of the crop, growth of weeds, infections and infestations.
Growing soyabean in the field will improve soil structure and fertility as it will draw water and nutrients from different level and add nitrogen salts. Weeds, soil borne pathogens and pests of wheat crop will be eliminated as they do not find their host.

More Resources

• Value Based Questions in Science for Class 9
• HOTS Questions for Class 9 Science
• NCERT Solutions for Class 9 Science
• NCERT Exemplar Solutions for Class 9 Science
• Previous Year Question Papers for CBSE Class 9 Science

Question 2.
Why should fumigation be preferred over spraying in godowns ?
Answer:

1. In fumigation, the worker does not come in contact with the fumigant. There is some contact with the pesticide during spraying. In spraying, the worker suffers irritation in eyes, nose, vomiting, etc.
2. No residue remains over articles in fumigation. In spraying some residue can enter the sprayed articles.
3. Fumigants are volatile while sprays are seldom volatile.
4. Fumigation disinfects the whole area. Spraying disinfects only the sprayed articles.
5. The volume of fumigant is small while the volume of sprayed pesticide is generally large.

Question 3.
What is the need of crossing the exotic cattle with Indian cattle when exotic cattle have higher yield as compared to the hybrid cattle ?
Answer:
There is no doubt that the hybrid produced by cross breeding exotic breed with local breed yields less milk as compared to the exotic breed. However, exotic breed cannot be incorporated in our dairy farms and farm houses due to :

1. Different climatic conditions. Most of the exotic breeds have come from colder countries. Colder areas are limited in our country.
2. The exotic breeds will fall prey to local pests and pathogens easily as they are not resistant to them.
3. The feed available locally does not match with the feed required by the exotic breeds.
   Therefore, there is no alternative bur to import a few exotic cattle and cross-breed them with local cattle for obtaining hybrid cattle acclimitised to local climate and resistant to local diseases.

Question 4.
Why should organic foods be preferred over conventional foods ?
Answer:
The conventional foods are raised using chemical fertilizers and chemical pesticides. These agrochemicals pass into conventional foods in small traces. Repeated use of conventional foods increases the concentration of agrochemicals in our bodies. They become toxic. As a result a number of ailments and harms can occur to us.
On the other hand, organic foods are free from any traces ol agrochemicals as they are raised by using manures, biofertilizers and biopesticides. Being nontoxic, organic foods should be preferred over conventional foods. Agrochemicals used in raising conventional foods are highly pollutants. They pollute soil, ground water and surface waters. Eutrophication of ponds and lakes is due to them. Manure used in raising organic foods is environmentally clean method of disposing off and recycling organic wastes.

Hope given Value Based Questions in Science for Class 9 Chapter 15 Improvement in Food Resources are helpful to complete your science homework.

If you have any doubts, please comment below. Learn Insta try to provide online science tutoring for you.