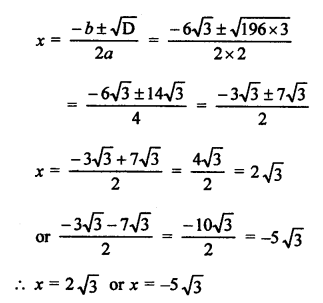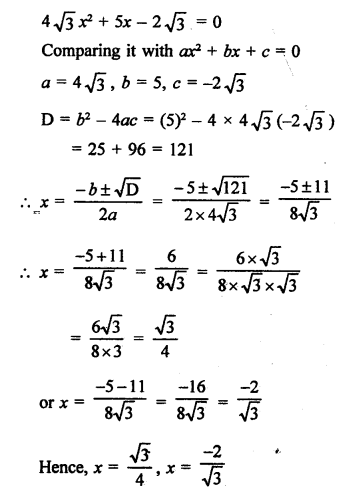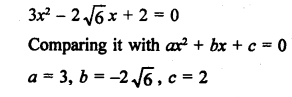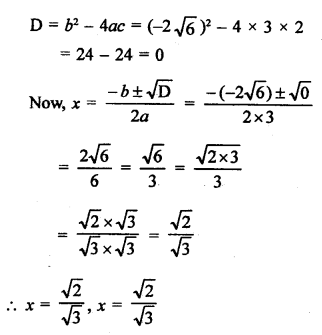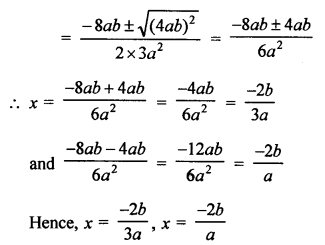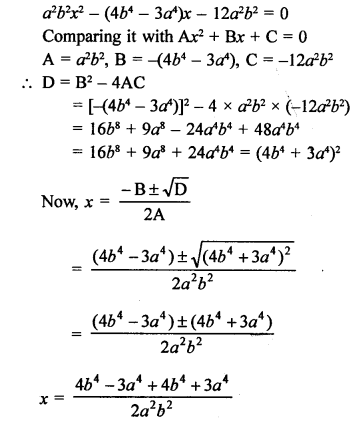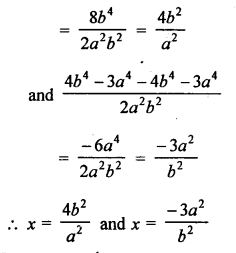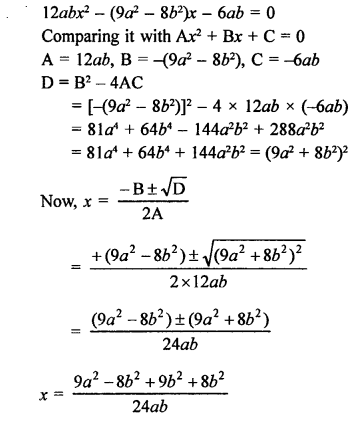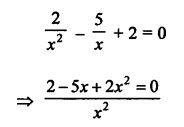Prasanna

RS Aggarwal Class 9 Solutions Chapter 14 Statistics Ex 14E

These Solutions are part of RS Aggarwal Solutions Class 9. Here we have given RS Aggarwal Solutions Class 9 Chapter 14 Statistics Ex 14E.

Other Exercises

• RS Aggarwal Solutions Class 9 Chapter 14 Statistics Ex 14A
• RS Aggarwal Solutions Class 9 Chapter 14 Statistics Ex 14B
• RS Aggarwal Solutions Class 9 Chapter 14 Statistics Ex 14C
• RS Aggarwal Solutions Class 9 Chapter 14 Statistics Ex 14D
• RS Aggarwal Solutions Class 9 Chapter 14 Statistics Ex 14E
• RS Aggarwal Solutions Class 9 Chapter 14 Statistics Ex 14F
• RS Aggarwal Solutions Class 9 Chapter 14 Statistics Ex 14G
• RS Aggarwal Solutions Class 9 Chapter 14 Statistics Ex 14H

Question 1.
Solution:
Mean marks of 7 students = 226
∴Total marks of 7 students = 226 x 1 = 1582
Marks obtained by 6 of them are 340, 180, 260, 56, 275 and 307
∴ Sum of marks of these 6 students = 340 + 180 + 260 + 56 + 275 + 307 = 1418
∴ Marks obtained by seventh student = 1582 – 1418 = 164 Ans.

Question 2.
Solution:
Mean weight of 34 students = 46.5 kg.
∴ Total weight of 34 students = 46.5 x 34 kg = 1581 kg
By including the weight of teacher, the mean weight of 35 persons = 500 g + 46.5 kg
= 46.5 + 0.5 = 47.0 kg
∴ Total weight = 47.0 x 35 = 1645 kg
∴ Weight of the teacher = (1645 – 1581) kg = 64 kg Ans.

Question 3.
Solution:
Mean weight of 36 students = 41 kg
∴ Total weight of 36 students = 41 x 36 kg = 1476 kg
After leaving one student, number of students = 36 – 1 =35
Their new mean = 41.0 – 200g = (41.0 – 0.2) kg = 40.8 kg.
∴ Total weight of 35 students = 40.8 x 35 = 1428 kg
∴ Weight of leaving student = (1476 – 1428) kg = 48 kg Ans.

Question 4.
Solution:
Average weight of 39 students = 40 kg
∴ Total weight of 39 students = 40 x 39 = 1560 kg
By admitting of a new student, no. of students = 39 + 1 =40
and new mean = 40 kg – 200 g = 40 kg – 0.2 kg = 39.8 kg
∴Weight of 40 students = 39.8 x 40 kg = 1592 kg
∴Weight of new student = 1592 – 1560 kg = 32 kg Ans.

Question 5.
Solution:
Average salary of 20 workers = Rs. 7650
∴Their total salary = Rs. 7650 x 20 = Rs. 153000
By adding the salary of the manager, their mean salary = Rs. 8200
∴Their total salary = Rs. 8200 x 21 = Rs. 172200
∴Salary of the manager = Rs. 172200 – Rs. 153000 = Rs. 19200 Ans.

Question 6.
Solution:
Average wage of 10 persons = Rs. 9000
Their total wage = Rs. 9000 x 10 = Rs. 90000
Wage of one person among them = Rs. 8100
and wage of new member = Rs. 7200
∴ New total wage = Rs. (90000 – 8100 + 7200) = Rs. 89100
Their new mean wage = Rs.\(\frac { 89100 }{ 10 } \) = Rs. 8910

Question 7.
Solution:
Mean consumption of petrol for 7 months of a year = 330 litres
Mean consumption of petrol for next 5 months = 270 litres
∴Total consumption for first 7 months = 7 x 330 = 2320 l
and total consumption for next 5 months = 5 x 270 = 1350 l
Total consumption for 7 + 5 = 12 months = 2310 + 1350 = 3660 l
Average consumption = \(\frac { 3660 }{ 12 } \) = 305 liters per month.

Question 8.
Solution:
Total numbers of numbers = 25
Mean of 15 numbers = 18
∴Total of 15 numbers = 18 x 15 = 270
Mean of remaining 10 numbers = 13
∴Total = 13 x 10 = 130
and total of 25 numbers = 270 + 130 = 400
∴Mean = \(\frac { 400 }{ 25 } \) = 16 Ans.

Question 9.
Solution:
Mean weight of 60 students = 52.75 kg.
Total weight = 52.75 x 60 = 3165 kg
Mean of 25 out of them = 51 kg.
∴Their total weight = 51 x 25 = 1275 kg
∴ Total weight of remaining 60 – 25 = 35 students = 3165 – 1275 = 1890 kg 1890
Mean weight = \(\frac { 1890 }{ 35 } \) = 54 kg Ans.

Question 10.
Solution:
Average increase of 10 oarsman = 1.5 kg.
∴ Total increased weight =1.5 x 10 = 15kg
Weight of out going oarsman = 58 kg .
∴ Weight of new oarsman = 58 + 15 = 73 kg Ans.

Question 11.
Solution:
Mean of 8 numbers = 35
∴Total of 8 numbers = 35 x 8 = 280
After excluding one number, mean of 7 numbers = 35 – 3 = 32
Total of 7 numbers = 32 x 7 = 224
Hence excluded number = 280 – 224 = 56 Ans.

Question 12.
Solution:
Mean of 150 items = 60
Total of 150 items = 60 x 150 = 9000
New total = 9000 + 152 + 88 – 52 – 8 = 9000 + 240 – 60 = 9180
∴New mean = \(\frac { 9180 }{ 150 } \) = 61.2 Ans.

Question 13.
Solution:
Mean of 31 results = 60
∴Total of 31 results = 60 x 31 = 1860
Mean of first 16 results = 58
∴Total of first 16 results = 58 x 16 = 928
and mean of last 16 results = 62
∴Total of last 16 results = 62 x 16 = 992
∴16th result = (928 + 992) – 1860 = 1920 – 1860 = 60 Ans.

Question 14.
Solution:
Mean of 11 numbers = 42
∴Total of 11 numbers = 42 x 11 = 462
Mean of first 6 numbers = 37
∴Total of first 6 numbers = 37 x 6 = 222
Mean of last 6 numbers = 46
∴Total of last 6 numbers = 46 x 6 = 276
∴6th number = (222 + 276) – 462 = 498 – 462 = 36 Ans.

Question 15.
Solution:
Mean weight of 25 students = 52 kg
∴ Total weight of 25 students = 52 x 25 = 1300 kg
Mean weight of first 13 students = 48 kg
∴ Total weight of first 13 students = 48 x 13 kg = 624 kg
Mean of last 13 students = 55 kg
∴Total of last 13 students = 55 x 13 kg = 715 kg
∴Weight of 13th student = (624 + 715) – 1300 = 1339 – 1300 = 39 kg Ans.

Question 16.
Solution:
Mean of 25 observations = 80
Total of 25 observations = 80 x 25 = 2000
Mean of another 55 observations = 60
∴ Total of these 55 observations = 60 x 55 = 3300
Total number of observations = 25 + 55 = 80
and total of 80 numbers = 2000 + 3300 = 5300
Mean of 80 observations = \(\frac { 5300 }{ 80 } \) = 66.25 Ans.

Question 17.
Solution:
Marks in English = 36
Marks in Hindi = 44
Marks in Mathematics = 75
Marks in Science = x
∴Total number of marks in 4 subjects = 36 + 44 + 75 + x = 155 + x
Average marks in 4 subjects = 50
∴Total marks = 50 x 4 = 200
∴155 + x = 200
=> x = 200 – 155
=> x = 45
Hence, marks in Science = 45 Ans.

Question 18.
Solution:
Mean of monthly salary of 75 workers = Rs. 5680
Total salary of 75 workers = Rs. 5680 x 75 = Rs. 426000
Mean salary of 25 among them = Rs. 5400
Total of 25 workers = Rs. 5400 x 25 = Rs. 135000
Mean salary of 30 among them = Rs. 5700
∴Total of 30 among them = Rs. 5700 x 30 = Rs. 171000
∴ Total salary of 25 + 30 = 55 workers = Rs. 135000 + 171000 = Rs. 306000
∴Total salary of remaining 75 – 55 = 20 workers = Rs. 426000 – 306000 = Rs. 120000
∴ Mean of remaining 20 workers = Rs. \(\frac { 120000 }{ 20 } \) = Rs. 6000 Ans.

Question 19.
Solution:
Let distance between two places = 60 km
∴Time taken at the speed of 15 km/h = \(\frac { 60 }{ 15 } \) = 4 hours
and time taken at speed of 10 km/h for coming back = \(\frac { 60 }{ 10 } \) = 6 hours
Total the taken = 4 + 6 = 10
hours and distance covered = 60 + 60 = 120 km
∴Average speed = \(\frac { 120 }{ 10 } \) =12 km/hr.

Question 20.
Solution:
No. of total students = 50
No. of boys = 40
∴ No. of girls = 50 – 40 = 10
Average weight of class = 44kg
∴Total weight of 50 students = 44 x 50 = 2200 kg
Average weight of 10 girls = 40 kg
∴Total weight = 40 x 10 = 400 kg
Total weight of 40 boys = 2200 – 400 = 1800 kg
∴Average weight of 40 boys = \(\frac { 1800 }{ 40 } \)kg = 45 kg Ans.

Hope given RS Aggarwal Solutions Class 9 Chapter 14 Statistics Ex 14E are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 10 Solutions Chapter 10 Quadratic Equations Ex 10C

These Solutions are part of RS Aggarwal Solutions Class 10. Here we have given RS Aggarwal Solutions Class 10 Chapter 10 Quadratic Equations Ex 10C.

Other Exercises

• RS Aggarwal Solutions Class 10 Chapter 10 Quadratic Equations Ex 10A
• RS Aggarwal Solutions Class 10 Chapter 10 Quadratic Equations Ex 10B
• RS Aggarwal Solutions Class 10 Chapter 10 Quadratic Equations Ex 10C
• RS Aggarwal Solutions Class 10 Chapter 10 Quadratic Equations Ex 10D
• RS Aggarwal Solutions Class 10 Chapter 10 Quadratic Equations Ex 10E
• RS Aggarwal Solutions Class 10 Chapter 10 Quadratic Equations Test Yourself

Find the discriminant of each of the following equations:
Question 1.
Solution:

Find the roots of each of the following equations, if they exist, by applying the quadratic formula:
Question 2.
Solution:

Question 3.
Solution:

x = 3 + √5 or x = 3 – √5

Question 4.
Solution:

Question 5.
Solution:

Question 6.
Solution:

Question 7.
Solution:

Question 8.
Solution:

Question 9.
Solution:

Question 10.
Solution:

Question 11.
Solution:

Question 12.
Solution:

Question 13.
Solution:

Question 14.
Solution:

Question 15.
Solution:

Question 16.
Solution:
x² + x + 2 = 0
Comparing it with ax² + bx + c = 0
a = 1, b = 1, c = 2
D = b² – 4ac = (1)² – 4 x 1 x 2 = 1 – 8 = -7
D < 0
There are no real roots.

Question 17.
Solution:

Question 18.
Solution:

Question 19.
Solution:

Question 20.
Solution:
3x² – 2x + 2 = 0
Comparing it with ax² + bx + c = 0
a = 3, b = -2, c = 2
D = b² – 4ac = (-2 )² – 4 x 3 x 2 = 4 – 24 = -20
D < 0
Roots are not real.

Question 21.
Solution:

Question 22.
Solution:

Question 23.
Solution:

Question 24.
Solution:

Question 25.
Solution:

Question 26.
Solution:

Question 27.
Solution:

x = (a + 2b) and x = (a – 2b)

Question 28.
Solution:

Question 29.
Solution:

Question 30.
Solution:

Question 31.
Solution:

Question 32.
Solution:

Question 33.
Solution:

Question 34.
Solution:

Question 35.
Solution:

Question 36.
Solution:

Hope given RS Aggarwal Solutions Class 10 Chapter 10 Quadratic Equations Ex 10C are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 9 Solutions Chapter 14 Statistics Ex 14D

These Solutions are part of RS Aggarwal Solutions Class 9. Here we have given RS Aggarwal Solutions Class 9 Chapter 14 Statistics Ex 14D.

Other Exercises

• RS Aggarwal Solutions Class 9 Chapter 14 Statistics Ex 14A
• RS Aggarwal Solutions Class 9 Chapter 14 Statistics Ex 14B
• RS Aggarwal Solutions Class 9 Chapter 14 Statistics Ex 14C
• RS Aggarwal Solutions Class 9 Chapter 14 Statistics Ex 14D
• RS Aggarwal Solutions Class 9 Chapter 14 Statistics Ex 14E
• RS Aggarwal Solutions Class 9 Chapter 14 Statistics Ex 14F
• RS Aggarwal Solutions Class 9 Chapter 14 Statistics Ex 14G
• RS Aggarwal Solutions Class 9 Chapter 14 Statistics Ex 14H

Question 1.
Solution:
(i) First eight natural numbers are 1, 2, 3, 4, 5, 6, 7, 8
∴ Mean = \(\frac { 1+2+3+4+5+6+7+8 }{ 8 } \) = \(\frac { 36 }{ 8 } \) = \(\frac { 9 }{ 2 } \) = 4.5
(ii) First ten odd numbers are 1, 3, 5, 7, 9, 11, 13, 15, 17, 19
∴ Mean = \(\frac { 1+3+5+7+9+11+13+15+17+179 }{ 10 } \) = \(\frac { 100 }{ 10 } \) = 10
(iii) First five prime numbers are 2, 3, 5, 7, 11.
∴ Mean = \(\frac { 2+3+5+7+11 }{ 5 } \) = \(\frac { 28 }{ 5 } \) = 5.6
(iv) First six even numbers are 2, 4, 6, 8, 10, 12
∴ Mean = \(\frac { 2+4+6+8+10+12 }{ 10 } \) = \(\frac { 42 }{ 6 } \) = 7
(v) First seven multiples of 5 are 5, 10, 15, 20, 25, 30, 35
∴ Mean = \(\frac { 5+10+15+20+25+30+35 }{ 7 } \) = \(\frac { 140 }{ 7 } \) = 20
(vi) All the factors of 20 are, 1, 2, 4, 5, 10, 20
∴ Mean = \(\frac { 1+2+4+5+10+20 }{ 6 } \) = \(\frac { 42 }{ 6 } \) = 7

Question 2.
Solution:
No. of families (n) = 10
Sum of children (∑x1) = 2 + 4 + 3 + 4 + 2 + 0 + 3 + 5 + 1 + 6 = 30
∴ Mean \(\left( \overline { x } \right) =\frac { \sum { x1 } }{ n } =\frac { 30 }{ 10 } =3\)

Question 3.
Solution:
Here number of days (n) = 7
Number of books (∑x1) = 105 + 216 + 322 + 167 + 273 + 405 + 346 = 1834
∴ Mean \(\left( \overline { x } \right) =\frac { \sum { x1 } }{ n } =\frac { 1864 }{ 7 } =262 books\)

Question 4.
Solution:
Number of days (n) = 6
Sum of temperature (∑x) = 35.5 + 30.8 + 27.3 + 32.1 + 23.8 + 29.9 = 179.4°F
∴ Mean temperature = \(\frac { \sum { x } }{ n } =\frac { 179.4 }{ 6 } \)=29.9°F

Question 5.
Solution:
Number of students (n) = 12
Sum of marks (∑x) = 64 + 36 + 47 + 23 + 0 + 19 + 81 + 93 + 72 + 35 + 3 + 1 = 474
= \(\frac { \sum { x1 } }{ n } =\frac { 474 }{ 12 } \) = 39.5

Question 6.
Solution:
Here, n = 6
and arithmetic mean =13
Total sum = 13 x 6 = 78.
But sum of 7 + 9+ 11 + 13 + 21=61
Value of x = 78 – 61 = 17
Hence x = 17 Ans.

Question 7.
Solution:
Let x₁, x₂, x₃, … x₂₄ be the 24 numbers
\(\frac { x1+x2+x3+…..+x24 }{ 24 } =35\)
=> x₁ + x₂ + x₃ +….+ x₂₄ = 35 x 24

Question 8.
Solution:
Let x₁ + x₂ + x₃……..x₂₀ be the 20 numbers

Question 9.
Solution:
Let x₁, x₂, x₃ … x₁₅ be the numbers
Mean = \(\frac { x1+x2+x3+…..+x15 }{ 15 } = 27\)

Question 10.
Solution:
Let x₁, x₂, x₃ … x₁₂ be the numbers
Mean = \(\frac { x1+x2+x3+…..+x12 }{ 12 }\) = 40
=> x1+x2+x3+….+x12 = 40 X 12 =480
Now,new numbers are \(\frac { x1 }{ 8 } ,\frac { x2 }{ 8 } ,\frac { x3 }{ 8 } ,..\frac { x12 }{ 8 } \)
Mean = \(\frac { \frac { x1 }{ 8 } +\frac { x2 }{ 8 } +\frac { x3 }{ 8 } +…..+\frac { x12 }{ 8 } }{ 12 } \)
= \(\frac { 1 }{ 8 } \frac { \left( x1+x2+x3+….x12 \right) }{ 12 } \)
= \(\frac { 480 }{ 8X12 } \) = 5
Mean of new numbers =5

Question 11.
Solution:
Let x₁, x₂, x₃,…..x₂₀ are the numbers
Mean = \(\frac { x1+x2+x3+…x20 }{ 20 }\) = 18
=> x₁ + x₂ + x₃ +….+ x₂₀ = 18 X 20 =360

Question 12.
Solution:
Mean weight of 6 boys = 48 kg
Their total weight = 48 x 6 = 288 kg
Weights of 5 boys among them, are 51 kg, 45 kg, 49 kg, 46 kg and 44 kg
Sum of weight of 5 boys = (51 + 45 + 49 + 46 + 44) kg = 235 kg
Weight of 6th boy = 288 kg – 235 kg = 53 kg Ans.

Question 13.
Solution:
Mean of 50 students = 39
Total score = 39 x 50 = 1950
Now correct sum of scores = 1950 – Wrong item + Correct item= 1950 – 23 + 43
= 1950 + 20 = 1970
Correct mean = \(\frac { 1970 }{ 50 } \) = 39.4 Ans.

Question 14.
Solution:
Mean of 100 items = 64
The sum of 100 items = 64 x 100 = 6400
New sum of 100 items = 6400 + 36 + 90 – 26 – 9 = 6526 – 35 = 6491,
Correct mean = \(\frac { 6491 }{ 100 }\) =64.91 = 64.91 Ans.

Question 15.
Solution:
Mean of 6 numbers = 23
Sum of 6 numbers = 23 x 6 = 138
Excluding one number, the mean of remaining 5 numbers = 20
Total of 5 numbers = 20 x 5 = 100
Excluded number = 138 – 100 = 38 Ans.

Hope given RS Aggarwal Solutions Class 9 Chapter 14 Statistics Ex 14D are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 10 Solutions Chapter 10 Quadratic Equations Ex 10B

These Solutions are part of RS Aggarwal Solutions Class 10. Here we have given RS Aggarwal Solutions Class 10 Chapter 10 Quadratic Equations Ex 10B.

Other Exercises

• RS Aggarwal Solutions Class 10 Chapter 10 Quadratic Equations Ex 10A
• RS Aggarwal Solutions Class 10 Chapter 10 Quadratic Equations Ex 10B
• RS Aggarwal Solutions Class 10 Chapter 10 Quadratic Equations Ex 10C
• RS Aggarwal Solutions Class 10 Chapter 10 Quadratic Equations Ex 10D
• RS Aggarwal Solutions Class 10 Chapter 10 Quadratic Equations Ex 10E
• RS Aggarwal Solutions Class 10 Chapter 10 Quadratic Equations Test Yourself

Solve each of the following equations by using the method of completing the square:
Question 1.
Solution:
x² – 6x + 3 = 0
=> x² – 2 x 3 x x = -3

Question 2.
Solution:

Question 3.
Solution:

Question 4.
Solution:

Question 5.
Solution:

Question 6.
Solution:

Question 7.
Solution:

Question 8.
Solution:

Question 9.
Solution:

Question 10.
Solution:

Question 11.
Solution:

Question 12.
Solution:

Question 13.
Solution:

Question 14.
Solution:

Question 15.
Solution:

Question 16.
Solution:

Hope given RS Aggarwal Solutions Class 10 Chapter 10 Quadratic Equations Ex 10B are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 9 Solutions Chapter 14 Statistics Ex 14C

These Solutions are part of RS Aggarwal Solutions Class 9. Here we have given RS Aggarwal Solutions Class 9 Chapter 14 Statistics Ex 14C.

Other Exercises

• RS Aggarwal Solutions Class 9 Chapter 14 Statistics Ex 14A
• RS Aggarwal Solutions Class 9 Chapter 14 Statistics Ex 14B
• RS Aggarwal Solutions Class 9 Chapter 14 Statistics Ex 14C
• RS Aggarwal Solutions Class 9 Chapter 14 Statistics Ex 14D
• RS Aggarwal Solutions Class 9 Chapter 14 Statistics Ex 14E
• RS Aggarwal Solutions Class 9 Chapter 14 Statistics Ex 14F
• RS Aggarwal Solutions Class 9 Chapter 14 Statistics Ex 14G
• RS Aggarwal Solutions Class 9 Chapter 14 Statistics Ex 14H

Question 1.
Solution:
It is clear that the given frequency distribution is in exclusive form, we represent the daily wages (in rupees) along x-axis and no. of workers along y-axis. Then we construct rectangles with class intervals as bases and corresponding frequencies as heights as shown given below:

Question 2.
Solution:
We shall take daily earnings along x-axis and number of stores along y-axis. Then we construct rectangles with the given class intervals as bases and corresponding frequency as height as shown in the graph.

Question 3.
Solution:
We shall take heights along x-axis and number of students along y-axis. Then we shall complete the rectangles with the given class intervals as bases and frequency as height and complete the histogram as shown below :

Question 4.
Solution:
We shall take class intervals along x-axis and frequency along y-axis Then we shall complete the rectangles with given class interval as bases and frequency as heights and complete the histogram as shown below.

Question 5.
Solution:
The given frequency distribution is in inclusive form first we convert it into exclusive form at given below.


Now, we shall take class intervals along x-axis and frequency along y-axis and draw rectangles with class intervals as bases and frequency as heights and complete the histogram as shown.

Question 6.
Solution:

Question 7.
Solution:
In the given distribution class intervals are different size. So, we shall calculate the adjusted frequency for each class. Here minimum class size is 4. We know that adjusted
frequency of the class is \(\frac { max\quad class\quad size }{ class\quad size\quad of\quad this\quad class } \)  x its frequency

Question 8.
Solution:
We shall take two imagined classes one 0-10 at the beginning with zero frequency a id other 70-80 at the end with zero frequency.


Now, plot the points” (5, 0), (15, 2), (25, 5), (35, 12), (45, 19), (55, 9), (65, 4), (75, 0) on the graph and join them its order to get a polygon as shown below.

Question 9.
Solution:
We take Age (in years) along x-axis and number of patients along y-axis. First we complete the histogram and them join the midpoints of their tops in order

We also take two imagined classes. One 0-10 at the beginning and other 70-80 at the end and also join their midpoints to complete the polygon as shown.

Question 10.
Solution:
We take class intervals along x-axis and frequency along y-axis.
First we complete the histogram and then join the midpoints of the tops of adjacent rectangles in order. We shall take two imagined classes 15-20 at the beginning and 50-55 at the end.
We also join their midpoints to complete the polygon as shown

Question 11.
Solution:
We represent class interval on x-axis and frequency on y-axis. First we construct the histogram and then join the midpoints of the tops of each rectangle by line segments. We shall take two imagined class i.e. 560-600 at the beginning and 840-900 at the end. Join their midpoints also to complete

Question 12.
Solution:
We will take the imagined class 11-0 at the beginning and 61-70 at the end. Each with frequency zero. Thus, we have,


Now we will mark the points A (-5.5, 0), B(5.5, 8), C(15.5, 3) D(25.5, 6), E(35.5, 12), F(45.5, 2), G(55.5, 7) and H(65.5, 0) on the graph and join them in order to get the required frequency polygon.

Hope given RS Aggarwal Solutions Class 9 Chapter 14 Statistics Ex 14C are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.