Prasanna

NCERT Exemplar Solutions for Class 9 Science Chapter 7 Diversity in Living Organisms

by

NCERT Exemplar Solutions for Class 9 Science Chapter 7 Diversity in Living Organisms

These Solutions are part of NCERT Exemplar Solutions for Class 9 Science . Here we have given NCERT Exemplar Solutions for Class 9 Science Chapter 7 Diversity in Living Organisms

Question 1.
Write true (T) or false (F)
(a) Wittaker proposed five kingdom classification.
(b) Monera is divided into Archaebacteria and Eubacteria.
(c) Starting from Class, Species comes before Genus.
(d) Anabaena belongs to kingdom Monera.
(e) Blue-green algae belong to kingdom Protista.
(f) All prokaryotes are classified under Monera.
Answer:
(a) —T
(b) —T,
(c) — F
(d) —T,
(e) —F,
(f) —T.

More Resources

Question 2.
Fill in the blanks :
(a) Fungi show ……………. mode of nutrition.
(b) Cell wall of fungi is made up of ……………… .
(c) Association between blue-green algae and fungi is called as …………….. .
(d) Chemical nature of chidn is ……………… .
(e) ………………. has smallest number of organisms with maximum number of similar characters.
(f) ……………… are called amphibians of plant kingdom.
Answer:
(a) saprophytic
(b) chitin
(c) lichen
(d) carbohydrate
(e) Species
(f) Bryophytes.

Question 3.
You are provided with seeds of Gram, Wheat, Rice Pumpkin, Maize and Pea. Classify them whether they are monocot or dicot ?
Answer:
Gram-Dicot.
Wheat-Monocot.
Rice-Monocot.
Pumpkin-Dicot.
Maize-Monocot.
Pea-Dicot.

Question 4.
Match the items of Column A with items of Column B.
NCERT Exemplar Solutions for Class 9 Science Chapter 7 Diversity in Living Organisms image - 1
Answer:
(a) —(ii),
(b) —(i),
(c) — (iv),
(d) —(iii),
(e) — (vi),
(f) —(v),
(g) — (vii).

Question 5.
Match the articles of Column A with those of column B
NCERT Exemplar Solutions for Class 9 Science Chapter 7 Diversity in Living Organisms image - 2
Answer:
a —(iii),
b —(ii),
c—(vi),
d —(i),
e —(v),
f—(iv).

Question 6.
Classify the following organisms based on absence or presence of true coelom as acoelomate, pseudocoelomate and coelomate : Spongilla, Sea Anemone, Planaria, Liver Fluke, Wuchereria, Ascaris, Nereis, Earthworm, Scorpion, Birds, Fishes and Horse.
Answer:

  1. Spongilla-Acoelomaxe
  2. Sea Anemone-Acoelomate
  3. Planaria-Acoelomate
  4. Liver Fluke-Acoelomate
  5. Wuchereria— Pseudocoelomate
  6. Aszvzris-Pseudocoelomate
  7. Nereis-Coelomate
  8. Scorpion—Coelomate
  9. Earthworm-Coelomate
  10. Birds-Coelomate
  11. Fishes-Coelomate
  12. Horse-Coelomate.

Question 7.
Endoskeleton of fishes is made up of cartilage and bone. Classify the following fishes as cartilaginous or bony : Xorpedo, Sting Ray, Dog fish, Rohu, Angler Fish, Exocoetus.
Answer:

  1. Xorpedo—Cartilaginous
  2. Sting Ray-Cartilaginous
  3. Dog Fish-Cartilaginous
  4. Rohu-Bony
  5. Angler fish-Bony
  6. Exocoetus—Bony.

Question 8.
Classify the following based on number of chambers in their heart : Rohu, Scolidon, Salamander, Flying Lizard, King Cobra, Crocodile, Ostrich, Pigeon, Bat, Whale.
Answer:

  1. Rohu. 2-Chambered.
  2. Scoliodon. 2-chambered
  3. Frog. 3-chambered
  4. Salamander. 3-chambered
  5. Flying Lizard. Incompletely 4-chambered.
  6. King Cobra. Incompletely 4-chambered.
  7. Crocodile. 4-chambered
  8. Ostrich. 4-chambered
  9. Pigeon. 4-chambered
  10. Bat. 4-chambered
  11. Whale. 4-chambered.

Question 9.
Classify Rohu, Scoliodon, Flying Lizard, King Cobra, Frog, Salamander, Ostrich, Pigeon, Bat, Crocodile and Whale into cold blooded and warm blooded animals.
Answer:

  1. Rohu. Cold blooded
  2. Scoliodon. Cold blooded
  3. Flying Lizard. Cold blooded
  4. King Cobra. Cold Blooded
  5. Frog. Cold blooded
  6. Salamander. Cold blooded
  7. Ostrich. Warm blooded
  8. Pigeon. Warm blooded
  9. Bat. Warm blooded,
  10. Crocodile. Cold blooded
  11. Whale. Warm blooded.

Question 10.
Name two egg laying mammals.
Answer:

  1. Duck Billed Platypus
  2. Echidna

Question 11.
Fill in the blanks.
(a) Five Kingdom classification of living organisms is given by …………….. .
(b) Basic smallest unit of classification is …………. .
(c) Prokaryotes are grouped in kingdom …………. .
(d) Paramoecium is a protistan because of its ……………. .
(e) Fungi do not contain ……………. .
(f ) A fungus ………….. can be seen without microscope.
(g) Common fungus used in preparing the bread is …………… .
(h) Algae and fungi form symbiotic association called ……………. .
Answer:
(a) Whittaker
(b) species
(c) Monera
(d) unicellular eukaryotic nature
(e) chlorophyll
(f) like mushroom
(g) Yeast
(h) lichen.

Question 12.
Give True (T) and Flase (F) :
(a) Gymnosperms differ from angiosperms in having covered seeds.
(b) Non-flowering plants are called cryptogamae.
(c) Bryophytes have conducting tissue.
(d) Funaria is a moss.
(e) Compound leaves are found in many ferns.
(f) Seeds, contain embryo.
Answer:
(a) —F,
(b) —F,
(c) —F,
(d) —T,
(e) —T,
(f) —T.

Question 13.
Give examples for the following :
(a) Bilateral, dorsiventral symmetry is found in ……………. .
(b) Worm causing disease elephantiasis is ……………… .
(c) Open circulatory system is found in ………………. where coelomic cavity is filled with blood.
(d) …………….. are known to have pseudocoelom.
Answer:
(a) Liver Fluke/Lizard
(b) Wuchereria (Filarial Worm)
(c) Arthropods
(d) Nematodes (roundworms).

Question 14.
Label a, b, c and d in the given figure. Give the function of b.
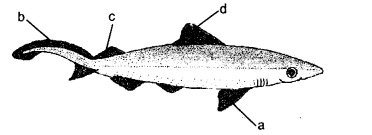
NCERT Exemplar Solutions for Class 9 Science Chapter 7 Diversity in Living Organisms image - 3
Answer:
a —pectoral fin.
b —caudal fin.
c—posterior dorsal fin,
d —anterior dorsal fin.
Function of b. Swimming and steering.

Question 15.
Fill the boxes with appropriate characteristics/plant group(s)
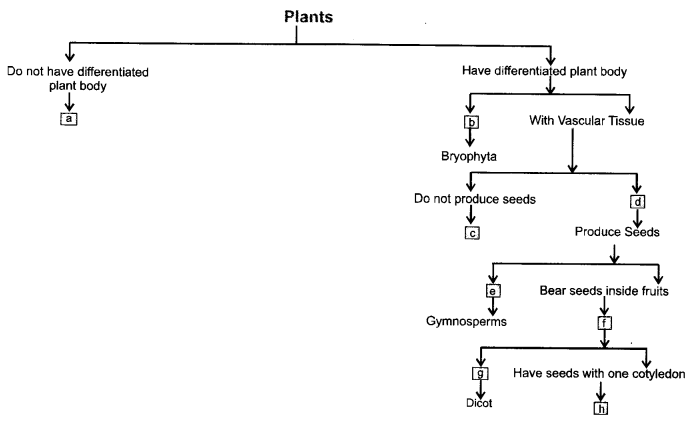
NCERT Exemplar Solutions for Class 9 Science Chapter 7 Diversity in Living Organisms image - 4
Answer:
a —Thallophyta.
b —Without specialized vascular tissue (non-vascular)
c —Pteridophyta.
d —Phanerogemae.
e —Bear naked seeds.
f—Angiosperms.
g—Have seeds with two cotyledons,
h —Monocots.

Question 16.
Write name of a few thallophytes. Draw a labelled diagram of Spirogyra.
Answer:
Ulothrix, Cladophora, JJlva, Spirogyra, Chara,
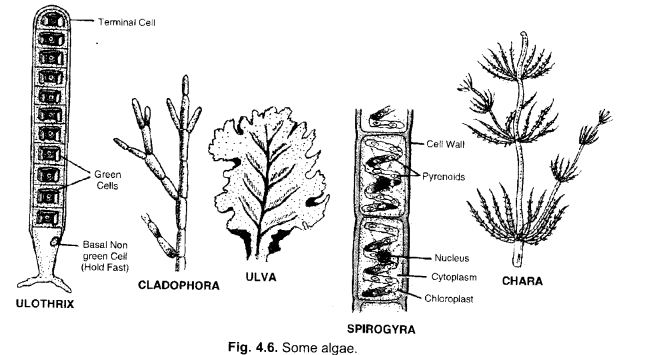
NCERT Exemplar Solutions for Class 9 Science Chapter 7 Diversity in Living Organisms image - 5

Question 17.
Thallophyta, bryophyta and pteridophyta one called “cryptogams.” Gymnosperms and angiosperns are called “phanerogams”. Discuss why ? Draw one example of gymnosperm. (CCE 2011)
Answer:
(a) Thallophyta, bryophyta and pteridophyta are called cryptogams because they are seedless and possesss inconspicuous or hidden reproductive organs.
(b) Gymnosperms and angiosperms are called phanerogams as they have conspicuous reproductive organs with seeds containing an embryo and reserve food.
(c)
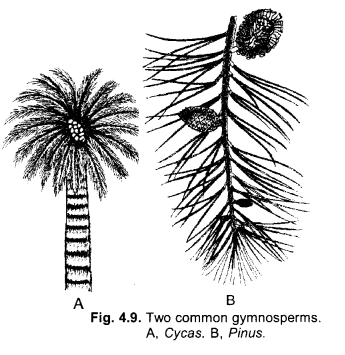
NCERT Exemplar Solutions for Class 9 Science Chapter 7 Diversity in Living Organisms image - 6

Question 18.
Define the terms and give one example of each
(a) Bilateral symmetry
(b) Coelom
(c) Triploblastic. (CCE 2011, 2012)
Answer:
(a) Bilateral Symmetry: It is a type of symmetry in which appendages and organs of the body are paired with one of each pair being present in right and left halves of the body, e.g., Lizard, Human.
(b) Coelom: It is mesoderm lined, fluid filled internal body cavity that lies between alimentary canal and skin. It provides a shock proof environment to the contained body organs, e.g, chordates, annelids.
(c) Triploblastic: They are animals having three germinal layers — outer ectoderm, middle mesoderm and inner endoderm, e.g, nematodes, arthropods, star fish.

Question 19.
You are given Leech, Nereis, Scolopendra, Prawn and Scorpio/i. All have segmented body organisation. Will you classify them in one group ? If not give the important characters based on which you will separate these, organisms into different groups.
(CCE 2012)
Answer:
No,

  1. Leech and Nereis have metameric segmentation (external segmentation corresponding to internal segmentation), closed circulatory system and unjointed appendages. They belong to annelida.
  2. Scolopendra, Prawn and Scorpion have open circulatory system and jointed appendages. They belong to arthropoda.

Question 20.
Which organism is more complex and evolved among bacteria, Mushroom and Mango tree ? Give reasons. (CCE 2012)
Answer:
Mango tree is more complex and evolved among bacteria, Mushroom and Mango because of the

  1. Differentiated sporophyte
  2. Vascular tissues
  3. Embryo stage
  4. Seeds present inside fruit. Bacteria are procaryotic. Mushroom is eucaryotic (fungus) but without any differentiation of stem leaves and roots, absence of vascular tissues and embryo stage.

Question 21.
Differentiate between flying Lizard and Bird. Draw the diagram.
Answer:
NCERT Exemplar Solutions for Class 9 Science Chapter 7 Diversity in Living Organisms image - 7
NCERT Exemplar Solutions for Class 9 Science Chapter 7 Diversity in Living Organisms image - 8
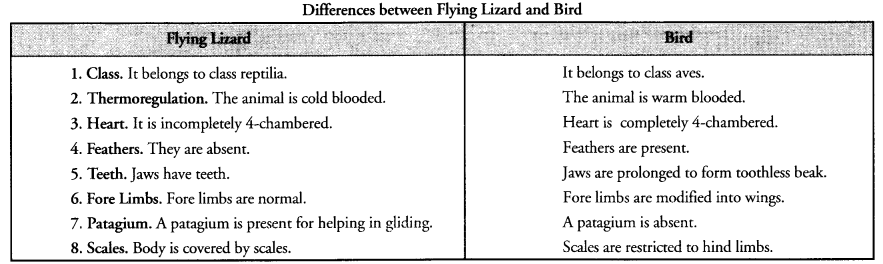
NCERT Exemplar Solutions for Class 9 Science Chapter 7 Diversity in Living Organisms image - 9

Question 22.
List out some common features in Cat, Rat and Bat. (CCE2012, 2013)
Answer:
Cat, Rat and Bat belong to same class of mammalia. The common features are

  1. Hair
  2. Mammary glands
  3. Integumentary glands
  4. Seven cervical vertebrae
  5. Diaphragm
  6. 4-Chambered heart
  7. External pinnae
  8. Vivipary.

Question 23.
Why do we keep both snake and turtle in the same class ? (CCE 2012)
Answer:
Both Snake and Turtle have been placed in class reptilia because of the common characteristics :

  1. Skin without glands
  2. Three chambered (incompletely four chambered) heart
  3. Respiration through lungs
  4. Cold blooded
  5. Hard shelled eggs
  6. Embryo protected by extra embryonal membranes.

Hope given NCERT Exemplar Solutions for Class 9 Science Chapter 7 Diversity in Living Organisms are helpful to complete your science homework.

If you have any doubts, please comment below. Learn Insta try to provide online science tutoring for you.

RS Aggarwal Class 8 Solutions Chapter 5 Playing with Numbers Ex 5B

by

RS Aggarwal Class 8 Solutions Chapter 5 Playing with Numbers Ex 5B

These Solutions are part of RS Aggarwal Solutions Class 8. Here we have given RS Aggarwal Solutions Class 8 Chapter 5 Playing with Numbers Ex 5B.

Other Exercises

Question 1.
Solution:
We know that a number is divisible by 2 if its unit digit is 0, 2, 4, 6 or 8
Therefore, (i) 94, (ii) 570, (iv) 2398,(v) 79532 and (vi) 13576 are divisible by 2.

Question 2.
Solution:
We know that a number is divisible by 5 if its unit digit is 0 or 5.
Therefore, (i) 95, (ii) 470, (iv) 2735, (vi) 35790, (vii) 98765 and (ix) 77990 are divisible by 5.

Question 3.
Solution:
We know that a number is divisible by 10 if its unit digit is zero.
Therefore, (ii) 90 and (iv) 57930 are divisible by 10.

Question 4.
Solution:
We know that a number is divisible by 3 if the sum of its digits is divisible by 3. Therefore
(i) 83 – 8 + 3 = 11,not divisible by 3
(ii) 378 – 3 + 7 + 8 = 18, is divisible by 3
(iii) 474 – 4 + 7 + 4 = 15, is divisible by 3
(iv) 1693 – 1 + 6 + 9 + 3 = 19, is divisible by 3
(v) 20345 – 2 + 0 + 3 + 4 + 5 = 14 is not divisible by 3
(vi) 67035 – 6 + 7 + 0 + 3 + 5 = 21 is divisible by 3
(vii)591282 – 5 + 9 + 1 + 2 + 8 = 27 is divisible by 3
(viii)903164 – 9 + 0 + 3 + 1 + 6 + 4 = 23,is not divisible by 3
(ix) 100002 – 1 + 0 + 0 + 0 + 0 + 2 = 3,is divisible by 3

Question 5.
Solution:
We know that a number is divisible by 9, if the sum of its digits is divisible by 9. Therefore,
(i) 327 = 3 + 2 + 7 = 12,is not divisible by 9
(ii) 7524 = 7 + 5 + 2 + 4 = 18, is divisible by 9
(iii) 32022 = 3 + 2 + 0 + 2 + 2 = 9,is divisible by 9
(iv) 64302 = 6 + 4 + 3 + 0 + 2 = 15, is not divisible by 9
(v) 89361= 8 + 9 + 3 + 6 + 1 = 27 is divisible by 9
(vi)14799 = 1 + 4 + 7 + 9 + 9 = 30,is not divisible by 9
(vii) 66888 = 6 + 6 + 8 + 8 + 8 = 36, is divisible by 9
(viii) 30006 = 3 + 0 + 0 + 0 + 6 = 9, is divisible by 9
(ix) 33333 = 3 + 3 + 3 + 3 + 3 = 15 is not divisible by 9

Question 6.
Solution:
We know that a number is divisible by 4, only when the number formed by its last two digits is divisible by 4.
Therefore,
(i) 134, is not divisible by 4 as last two digits 34 is not divisible by 4.
(ii) 618, is not divisible by 4 as last two digits 18 is not divisible by 4.
(iii) 3928, is divisible by 4 as last two digits 28 is divisible by 4.
(iv) 50176, is not divisible by 4 as last two digits 76 is not divisible by 4.
(y) 39392, is not divisible by 4 as last two digits 92 is not divisible by 4.
(vi) 56794, is not divisible by 4 as last two digits 94 is not divisible by 4.
(vii) 86102, is not divisible by 4 as last two digits 02 is not divisible by 4.
(viii) 66666, is not divisible by 4 as last two digits 66 is not divisible by 4.
(ix) 99918, is not divisible by 4 as last two digits 18 is not divisible by 4.
(x) 77736, is divisible by 4 as last two digits 36 is divisible by 4.

Question 7.
Solution:
A given number is divisible by 8 only when the number formed by its last three digits is divisible by 8.
(i) 6132, is not divisible by 8 as last three digits 132 is not divisible by 8.
(ii) 7304, is divisible by 8 as last three digits 304 is not divisible by 8.
(iii) 59312, is divisible by 8 as last three digits 312 is divisible by 8.
(iv) 66664, is divisible by 8 as last three digits 664 is divisible by 8.
(v) 44444, is not divisible by 8 as last three digits 444 is not divisible by 8.
(vi) 154360, is divisible by 8 as last three digits 360 is not divisible by 8.
(vii) 998818, is not divisible by 8 as last three digits 818 is not divisible by 8.
(viii) 265472, is divisible by 8 as last three digits 472 is divisible by 8.
(ix) 7350162, is not divisible by 8 as last three digits 162 is not divisible by 8.

Question 8.
Solution:
A given number is divisible by 11, if the difference between the sum of its digits at odd places and the sum of its digits at even places, is either O or a number divisible by 11.
(i) 22222
Sum of digit at odd places = 2 + 2 + 2 = 6
Sum of digit at even places = 2 + 2 = 4
Difference of the above sum = 6 – 4 =2,
which is not divisible by 11
22222 is not divisible by 11

(ii) 444444
Sum of digit at odd places = 4 + 4 + 4 = 12
Sum of digit at even places = 4 + 4 + 4 = 12
Difference of the above sum =(12 – 12) = O
444444 is divisible by 11

(iii) 379654
Sum of digit at odd places = 7 + 6 + 4 = 17
Sum of digit at even places = 3 + 9 + 5 = 17
Difference of the above sum = (17 – 17) = 0
379654 is divisible by 11

(iv) 1057982
Sum of digit at odd places = 1 + 5 + 9 + 2 = 17
Sum of digit at even places = 0 + 7 + 8 = 15
Difference of the above sum = (17 – 15) = 2, which is not divisible by 11
1057982 is not divisible by 11

(v) 6543207
Sum of digit at odd places = 6 + 4 + 2 + 7 = 19
Sum of digit at even places = 5 + 3 + 0 = 8
Difference of the above sum = (19 – 8) = 11, Which is divisible by 11
6543207 is divisible by 11

(vi) 818532
Sum of digital to odd places = 1 + 5 + 2 = 8
Sum of digit at even places = 8 + 8 + 3 = 19
Difference of the above sum = 19 – 8 = 11, which is divisible by 11
818532 is divisible by 11

(vii) 900163
Sum of digit at odd places = 0 + 1 + 3 = 4
Sum of digit at even places = 9 + 0 + 6 = 15
Difference of the above sum = (15 – 4) = 11, which is divisible by 11
900163 is divisible by 11

(viii) 7531622
Sum of digit at odd places = 7 + 3 + 6 + 2 = 18
Sum of digit at even places = 5 + 1 + 2 = 8
Difference of the above sum = (18 – 8) = 10, which is not divisible by 11
7531622 is not divisible by 11

Question 9.
Solution:
For testing the divisibility of a number by 7, we proceed according to the
following steps:
Step 1: Double the unit digit of the given number.
Step 2 : Subtract the above number from the number formed by excluding the unit digit of the given number.
Step 3 : 1f the number so obtained is divisible by 7 then the given number is divisible by 7.
(i) 693
Now, 69 – (2 x 3) = 63, which is divisible by 7
693 is divisible by 7

(ii) 7896
Now 789 – (6 x 2) = 777, which is divisible by 7
7896 is divisible by 7

(iii) 3467
Now, 346 – (7 x 2) = 332, which is not divisible by 7
3467 is not divisible by 7

(iv) 12873
Now,1287 – (3 x 2) = 1281, which is divisible by 7
12873 is divisible by 7

(v) 65436
Now, 6543 – (6 x 2) = 6531, which is divisible by 7
65436 is divisible by 7

(vi) 54636
Now, 5463 – (6 x 2) 5451, which is not divisible by 7
54636 is not divisible by 7

(vii) 98175
Now, 9817 – (5 x 2) 9807, which is divisible by 7
98175 is divisible by7

(viii) 88777
Now, 8877 – (7 x 2) = 8863, which is not divisible by 7
88777 is not divisible by 7

Question 10.
Solution:
The given number 7×3 is divisible by 3
The sum of its digits is divisible by 3
7 + x + 3 =>10 + x is divisible by 3
Value of x can be 2, 5, 8
The numbers can be 723, 753, 783

Question 11.
Solution:
The given number 53yl is divisible by 3
Sum of its digits is divisible by 3
i.e., 5 + 3 + y + 1 or 9 + y is divisible by 3
Values of y can be 0, 3, 6, 9
Then the numbers can be 5301, 5331, 5361, 5391

Question 12.
Solution:
Number x806 is divisible by 9
The sum of its digits is also divisible by 9
or x + 8 + 0 + 6 or 14 + x is divisible by 9
x can be 4
Number will be 4806

Question 13.
Solution:
The number 471z8 is divisible by 9
The sum of its digits is also divisible by 9
471z8 = 4 + 7 + 1 + z + 8
=> 20 + z is divisible by 9
Value of z can be 7
Number will be 47178

Question 14.
Solution:
Let the number 21, sum of digits 2 + 1 = 3
which is divisible by 3 not by 9
Let the number 24, sum of digits 2 + 4 = 6
which is divisible by 3 not by 9
Let the number 30, sum of digits 3+0 = 3
which is divisible by 3 not by 9
Let the number 33, sum of digits 3 + 3 = 6
which is divisible by 3 not by 9
Let the number by 39 sum of digits 3 + 9 = 12
which is divisible by 3 not by 9

Question 15.
Solution:
Consider numbers as 28, 36,44, 52,60 as these numbers are divisible by 4 not by 8.
Let the number 39, sum of digits 3 + 9 = 12
which is divisible by 3 not by 9

Hope given RS Aggarwal Solutions Class 8 Chapter 5 Playing with Numbers Ex 5B are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 8 Solutions Chapter 5 Playing with Numbers Ex 5A

by

RS Aggarwal Class 8 Solutions Chapter 5 Playing with Numbers Ex 5A

These Solutions are part of RS Aggarwal Solutions Class 8. Here we have given RS Aggarwal Solutions Class 8 Chapter 5 Playing with Numbers Ex 5A.

Other Exercises

Question 1.
Solution:
Let tens digit = x
Units digit = 3
∴Number = 3 + 10x
According to the condition,
7 (x + 3) = 3 + 10x
7x + 21 = 3 + 10x
21 – 3 = 10x – 7x
=> 3x = 18
x = \(\\ \frac { 18 }{ 3 } \)
∴Number = 3 + 10x
= 3 + 10 x 6 = 3 + 60 = 63

Question 2.
Solution:
Let ten’s digit = x
Then units digit = 2x
and number = 10x + 2x = 12x
According to the condition,
12x = x + 2x + 18
12x – x – 2x = 18
=> 9x = 18
x = \(\\ \frac { 18 }{ 9 } \) = 2
∴Number = 12x = 2 x 12 = 24

Question 3.
Solution:
Let units digit = x
and tens digit = y
Number = x + 10y
Now x + 10y = 4 (x + y) + 3
=> x + 10y = 4x + 4y + 3
10y – 4y – 4x + x = 3
=> 6y – 3x = 3
2y – x = 1 ….(i)
∴Number by reversing the order of digits = y + 10x
=>x + 10y + 18 = y + 10x
=>10x – x + y – 10y = 18
=> 9x – 9y = 18
x – y = 2 ….(ii)
∴Adding (i) and (ii)
=> 2y – y = 3
y = 3
x = 2y – 1 = 2 x 3 – 1 = 6 – 1 = 5
∴Number = x + 10y = 5 + 3 x 10
= 5 + 30 = 35

Question 4.
Solution:
Sum of two digits of a number =15
Let units digit = x
Then tens digit = 15 – x
∴Number = 10 (15 – x) + x
= 150 – 10x + x = 150 – 9x
By interchanging the digits, the new number will be
= 10x + 15 – x = 9x + 15
According to the condition,
9x + 15 = 9 + 150 – 9x
9x + 9x = 159-15 = 144
18x = 144
=>x = \(\\ \frac { 144 }{ 18 } \) = 8
∴Number = 150 – 9x = 150 – 9 x 8
= 150 – 72 = 78

Question 5.
Solution:
Let units place digit = x
and tens place digit = y
Then number = x + 10y
By interchanging the positions of the digits then
Units digits = y
and tens digit = x
∴Number = y + 10x
(x + 10y) – (y + 10x) = 63
=> x + 10y – y – 10x = 63
9y – 9x = 63
=> 9(y – x) = 63
y – x = \(\\ \frac { 63 }{ 9 } \) = 7
∴Hence, difference of its digits = 7 Ans.

Question 6.
Solution:
Sum of three digits of a number = 16
Let units digit of a three-digit number = x
Then tens digit = 3x
and hundreds digit = 4x
∴Number = x + 10 x 3x + 100 x 4x
= x + 30x + 400x = 431x
But x + 3x + 4x = 16 => 8x = 16
∴x = \(\\ \frac { 16 }{ 8 } \) = 2
∴Number = 431 x 862

 

Hope given RS Aggarwal Solutions Class 8 Chapter 5 Playing with Numbers Ex 5A are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 9 Solutions Chapter 13 Linear Equations in Two Variables VSAQS

by

RD Sharma Class 9 Solutions Chapter 13 Linear Equations in Two Variables VSAQS

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 13 Linear Equations in Two Variables VSAQS

Other Exercises

Question 1.
In a parallelogram ABCD, write the sum of angles A and B.
Solution:
In ||gm ABCD,
∠A + ∠B = 180°
(Sum of consecutive angles of a ||gm)
RD Sharma Class 9 Solutions Chapter 13 Linear Equations in Two Variables VSAQS Q1.1

Question 2.
In a parallelogram ABCD, if ∠D = 115°, then write the measure of ∠A.
Solution:
In ||gm ABCD,
∠D = 115°
But ∠A + ∠D = 180°
(Sum of consecutive angles of a ||gm)
RD Sharma Class 9 Solutions Chapter 13 Linear Equations in Two Variables VSAQS Q2.1
⇒ ∠A + 115°= 180° ∠A = 180°- 115°
∴ ∠A = 65°

Question 3.
PQRS is a square such that PR and SQ intersect at O. State the measure of ∠POQ.
Solution:
In a square PQRS,
Diagonals PR and QS intersects each other at O.
RD Sharma Class 9 Solutions Chapter 13 Linear Equations in Two Variables VSAQS Q3.1
∵ The diagonals of a square bisect each other at right angles.
∴ ∠POQ = 90°

Question 4.
If PQRS is a square then write the measure of ∠SRP.
Solution:
In square PQRS,
RD Sharma Class 9 Solutions Chapter 13 Linear Equations in Two Variables VSAQS Q4.1
Join PR,
∵Diagonals of a square bisect are opposite angles
∴∠SRP = \(\frac { 1 }{ 2 }\)x ∠SRQ
= \(\frac { 1 }{ 2 }\) x 90° = 45°

Question 5.
If ABCD is a rhombus with ∠ABC = 56°, find the measure of ∠ACD.
Solution:
In rhombus ABCD,
Diagonals bisect each other at 0 at right angles.
∠ABC = 56°
But ∠ABC + ∠BCD = 180° (Sum of consecutive angles)
⇒ 56° + ∠BCD = 180°
⇒ ∠BCD = 180° – 56° = 124°
∵ Diagonals of a rhombus bisect the opposite angle
∴ ∠ACD = \(\frac { 1 }{ 2 }\) ∠BCD = \(\frac { 1 }{ 2 }\) x 124°
= 62°
RD Sharma Class 9 Solutions Chapter 13 Linear Equations in Two Variables VSAQS Q5.1

Question 6.
The perimeter of a parallelogram is 22 cm. If the longer side measures 6.5 cm, what is the measure of the shorter side.
Solution:
Perimeter of a ||gm ABCD = 22cm
∴ Sum of two consecutive sides = \(\frac { 22 }{ 2 }\)
= 11cm
i.e. AB + BC = 11 cm
AB = 6.5 cm and let BC = x cm
∴ 6.5 + x = 11 cm
x = 11 – 6.5 = 4.5
∴ Shorter side = 4.5 cm
RD Sharma Class 9 Solutions Chapter 13 Linear Equations in Two Variables VSAQS Q6.1

Question 7.
If the angles of a quadrilateral are in the ratio 3 : 5 : 9 : 13. Then find the measure of the smallest angle.
Solution:
Ratio in the angles of a quadrilateral = 3 : 5 : 9 : 13
Let first angle = 3x
Second angle = 5x
Third angle = 9x
and fourth angle = 13x
∵ The sum of angles of a quadrilateral = 360°
∴ 3x + 5x + 9x + 13x = 360°
⇒ 30x = 360° ⇒ x = \(\frac { { 360 }^{ \circ } }{ 30 }\)  = 12
∴ Smallest angle = 3x = 3 x 12° = 36°

Question 8.
In parallelogram ABCD if ∠A = (3x – 20°), ∠B = (y + 15)°, ∠C = (x + 40°), then find the value of x and y.
Solution:
In a ||gm ABCD,
∠A = (3x – 20°), ∠B = y + 15°,
∠C = x + 40°
Now, ∠A = ∠C (Opposite angles of a ||gm)
⇒ 3x – 20 = x + 40°
⇒ 3x – x = 40° + 20° ⇒ 2x = 60°
⇒ x = \(\frac { { 60 }^{ \circ } }{ 2 }\)  = 30°
and ∠A + ∠B = 180° (Sum of the consecutive angles)
⇒ 3x-20° + y + 15° = 180°
⇒ 3x + y – 5° = 180°
⇒ 3 x 30° +y- 5° = 180°
⇒ 90° – 5° + y = 180
y = 180° – 90° + 5 = 95°
∴ x = 30°, y = 95°

Question 9.
If measures opposite angles of a parallelogram are (60 – x)° and (3x – 4)°, then find the measures of angles of the parallelogram.
Solution:
Opposite angles of a ||gm ABCD are (60 – x)° and (3x – 4°)
But opposite angles of a ||gm are equal, the
60° – x° = 3x – 4° ⇒ 60° + 4° = 3x + x
⇒ 4x = 64° ⇒ x = \(\frac { { 64 }^{ \circ } }{{ 4 }^{ \circ } }\)  = 16°
∴ ∠A = 60° – x = 60° – 16° = 44°
But ∠A + ∠B = 180° (sum of consecutive angle)
⇒ 44° + ∠B = 180°
⇒ ∠B = 180° – 44°
⇒ ∠B = 136°
But ∠A = ∠C and ∠B = ∠D (Opposite angles)
∴ Angles are 44°, 136°, 44°, 136°

Question 10.
In a parallelogram ABCD, the bisectors of ∠A also bisect BC at x, find AB : AD.
Solution:
In ||gm ABCD,
Bisectors of ∠A meets BC at X and BX = XC
Draw XY ||gm AB meeting AD at Y
RD Sharma Class 9 Solutions Chapter 13 Linear Equations in Two Variables VSAQS Q10.1
RD Sharma Class 9 Solutions Chapter 13 Linear Equations in Two Variables VSAQS Q10.2

Question 11.
In the figure, PQRS in an isosceles trapezium find x and y.
Solution:
∵ PQRS is an isosceles trapezium in which
SP = RQ and SR || PQ
∴ ∠P + ∠S = 180° (Sum of co-interior angles)
3x + 2x = 180° ⇒ 5x = 180°
⇒ x = \(\frac { { 180 }^{ \circ } }{ 5 }\)  = 36°
RD Sharma Class 9 Solutions Chapter 13 Linear Equations in Two Variables VSAQS Q11.1
But ∠P = ∠Qm (Base angles of isosceles trapezium)
y = 2x = 2 x 36° = 12°
∴ y = 12°
Hence x = 36°, y = 12°

Question 12.
In the figure ABCD is a trapezium. Find the values of x and y.
RD Sharma Class 9 Solutions Chapter 13 Linear Equations in Two Variables VSAQS Q12.1
Solution:
In trapezium ABCD,
AB || CD
RD Sharma Class 9 Solutions Chapter 13 Linear Equations in Two Variables VSAQS Q12.2
∴ ∠A + ∠D = 180° (Sum of cointerior angles)
x + 20° + 2x + 10° = 180°
3x + 30° = 180°
⇒ 3x= 180° – 30°
3x = 150°
x = \(\frac { { 150 }^{ \circ } }{ 3 }\)  = 50°
Similarly, ∠B + ∠C = 180°
⇒ y + 92° = 180°
⇒ y = 180° – 92° = 88°
∴ x = 50°, y = 88°

Question 13.
In the figure, ABCD and AEFG are two parallelograms. If ∠C = 58°, find ∠F.
RD Sharma Class 9 Solutions Chapter 13 Linear Equations in Two Variables VSAQS Q13.1
Solution:
In the figure, ABCD and AEFG are two parallelograms ∠C = 58°
RD Sharma Class 9 Solutions Chapter 13 Linear Equations in Two Variables VSAQS Q13.2
∵ DC || GF and CB || FE (Sides of ||gms)
∴ ∠C = ∠F
But ∠C = 58°
∴ ∠F = 58°

Question 14.
Complete each of the following statements by means of one of those given in brackets against each:
(i) If one pair of opposite sides are equal and parallel, then the figure is ……… (parallelogram, rectangle, trapezium)
(ii) If in a quadrilateral only one pair of opposite sides are parallel, the quadrilateral is …….. (square, rectangle, trapezium)
(iii) A line drawn from the mid-point of one side of a triangle ………. another side intersects the third side at its mid-point, (perpendicular to, parallel to, to meet)
(iv) If one angle of a parallelogram is a right angle, then it is necessarily a …….. (rectangle, square, rhombus)
(v) Consecutive angle of a parallelogram are ……… (supplementary, complementary)
(vi) If both pairs of opposite sides of a quadrilateral are equal, then it is necessarily a ……… (rectangle, parallelogram, rhombus)
(vii) If opposite angles of a quadrilateral are equal, then it is necessarily a ………. (parallelogram, rhombus, rectangle)
(viii)If consecutive sides of a parallelogram are equal, then it is necessarily a …….. (kite, rhombus, square)
Solution:
(i) If one pair of opposite sides are equal and parallel, then the figure is parallelogram.
(ii) If in a quadrilateral only one pair of opposite sides are parallel, the quadrilateral is trapezium.
(iii) A line drawn from the mid-point of one side of a triangle parallel to another side intersects the third side at its mid-point,
(iv) If one angle of a parallelogram is a right angle, then it is necessarily a rectangle.
(v) Consecutive angle of a parallelogram are supplementary.
(vi) If both pairs of opposite sides of a quadrilateral are equal, then it is necessarily a parallelogram.
(vii) If opposite angles of a quadrilateral are equal, then it is necessarily a parallelogram.
(viii) If consecutive sides of a parallelogram are equal, then it is necessarily a rhombus.

Question 15.
In a quadrilateral ABCD, bisectors of A and B intersect at O such that ∠AOB = 75°, then write the value of ∠C + ∠D.
Solution:
In quadrilateral ABCD,
Bisectors of ∠A and ∠B meet at O and ∠AOB = 75°
RD Sharma Class 9 Solutions Chapter 13 Linear Equations in Two Variables VSAQS Q15.1
In AOB, ∠AOB = 75°
∴ ∠OAB + ∠OBA = 180° – 75° = 105°
But OA and OB are the bisectors of ∠A and ∠B.
∴ ∠A + ∠B = 2 x 105° = 210°
But ∠A + ∠B + ∠C + ∠D = 360° (Sum of angles of a quad.)
∴ 210° + ∠C + ∠D = 360°
⇒ ∠C + ∠D = 360° – 210° = 150°
Hence ∠C + ∠D = 150°

Question 16.
The diagonals of a rectangle ABCD meet at O. If ∠BOC = 44° find ∠OAD.
Solution:
In rectangle ABCD,
Diagonals AC and BD intersect each other at O and ∠BOC = 44°
RD Sharma Class 9 Solutions Chapter 13 Linear Equations in Two Variables VSAQS Q16.1
But ∠AOD = ∠BOC (Vertically opposite angles)
∴ ∠AOD = 44°
In ∆AOD,
∠AOD + ∠OAD + ∠ODA = 180° (Sum of angles of a triangle)
⇒ 44° + ∠OAD + ∠OAD = 180° [∵ OA = OD, ∠OAD = ∠ODA]
⇒ 2∠OAD = 180° – 44° = 136°
∴ ∠OAD = \(\frac { { 136 }^{ \circ } }{ 2 }\)  = 68°

Question 17.
If ABCD is a rectangle with ∠BAC = 32°, find the measure if ∠DBC.
Solution:
In rectangle ABCD,
RD Sharma Class 9 Solutions Chapter 13 Linear Equations in Two Variables VSAQS Q17.1
Diagonals bisect each other at O
∠BAC = 32°
∵ OA = OB
∴ ∠OBA Or ∠DBA = ∠BAC = 32°
But ∠ABC = 90° (Angle of a rectangles)
∴ ∠DBC = ∠ABC – ∠DBA
= 90° – 32° = 58°

Question 18.
If the bisectors of two adjacent angles A and B of a quadrilateral ABCD intersect at a point O. Such that ∠C + ∠D = k(∠AOB), then find the value of k.
Solution:
In quadrilateral ABCD,
Bisectors of ∠A and ∠B meet at O
Such that ∠C + ∠D = k (∠AOB)
RD Sharma Class 9 Solutions Chapter 13 Linear Equations in Two Variables VSAQS Q18.1
RD Sharma Class 9 Solutions Chapter 13 Linear Equations in Two Variables VSAQS Q18.2

Question 19.
In the figure, PQRS is a rhombus in which the diagonal PR is produced to T. If ∠SRT = 152°, find x, y and z.
RD Sharma Class 9 Solutions Chapter 13 Linear Equations in Two Variables VSAQS Q19.1
Solution:
In rhombus PQRS,
Diagonal PR and SQ bisect each other at right angles and PR is produced to T such that ∠SRT = 152°
RD Sharma Class 9 Solutions Chapter 13 Linear Equations in Two Variables VSAQS Q19.2
But ∠SRT + ∠SRP = 180° (Linear pair)
⇒ 152° +∠SRP = 180°
⇒ ∠SRP =180°- 152° = 28°
But ∠SPR = ∠SRP (∵ PR bisects ∠P and ∠R)
⇒ z = 28°
y = 90° (∵ Diagonals bisect each other at right angles)
∠RPQ = z = 28°
∴ In ∆POQ,
z + x = 90° ⇒ 28° + x = 90°
⇒ x = 90° – 28° = 62°
∴ x = 62°, y = 90°, z = 28°

Question 20.
In the figure, ABCD is a rectangle in which diagonal AC is produced to E. If ∠ECD = 146°, find ∠AOB.
RD Sharma Class 9 Solutions Chapter 13 Linear Equations in Two Variables VSAQS Q20.1
Solution:
In rectangle ABCD,
Diagonals AC and BD bisect each other at O
AC is produced to E and ∠DCE = 146°
RD Sharma Class 9 Solutions Chapter 13 Linear Equations in Two Variables VSAQS Q20.2
∠DCE + ∠DCA = 180° (Linear pair)
⇒ 146°+ ∠DCA= 180°
⇒ ∠DCA = 180°- 146°
⇒ ∠DCA = 34°
∴ ∠CAB = ∠DCA (Alternate angles)
= 34°
Now in ∆AOB,
∠AOB = 180° – (∠DAB + ∠OBA)
= 180° – (34° + 34°)
= 1803 – 68° = 112°

Hope given RD Sharma Class 9 Solutions Chapter 13 Linear Equations in Two Variables VSAQS are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 8 Solutions Chapter 4 Cubes and Cube Roots Ex 4D

by

RS Aggarwal Class 8 Solutions Chapter 4 Cubes and Cube Roots Ex 4D

These Solutions are part of RS Aggarwal Solutions Class 8. Here we have given RS Aggarwal Solutions Class 8 Chapter 4 Cubes and Cube Roots Ex 4D.

Other Exercises

Objective Questions
Tick the correct answer in each of the following:

Question 1.
Solution:
(a) 141
= 3 x 47
RS Aggarwal Class 8 Solutions Chapter 4 Cubes and Cube Roots Ex 4D 1.1
RS Aggarwal Class 8 Solutions Chapter 4 Cubes and Cube Roots Ex 4D 1.2

Question 2.
Solution:
1152
= 2 x 2 x 2 x 2 x 2 x 2 x 3 x 3
RS Aggarwal Class 8 Solutions Chapter 4 Cubes and Cube Roots Ex 4D 2.1
RS Aggarwal Class 8 Solutions Chapter 4 Cubes and Cube Roots Ex 4D 2.2

Question 3.
Solution:
\(\sqrt [ 3 ]{ 512 }\)
RS Aggarwal Class 8 Solutions Chapter 4 Cubes and Cube Roots Ex 4D 3.1

Question 4.
Solution:
\(\sqrt [ 3 ]{ 125\times 64 }\)
RS Aggarwal Class 8 Solutions Chapter 4 Cubes and Cube Roots Ex 4D 4.1

Question 5.
Solution:
\(\sqrt [ 3 ]{ \frac { 64 }{ 343 } } \)
RS Aggarwal Class 8 Solutions Chapter 4 Cubes and Cube Roots Ex 4D 5.1

Question 6.
Solution:
\(\sqrt [ 3 ]{ \frac { -512 }{ 729 } } \)
RS Aggarwal Class 8 Solutions Chapter 4 Cubes and Cube Roots Ex 4D 6.1

Question 7.
Solution:
Factorising 648, we get
RS Aggarwal Class 8 Solutions Chapter 4 Cubes and Cube Roots Ex 4D 7.1

Question 8.
Solution:
Factorising 1536, we get
RS Aggarwal Class 8 Solutions Chapter 4 Cubes and Cube Roots Ex 4D 8.1

Question 9.
Solution:
\({ \left( 1\frac { 3 }{ 10 } \right) }^{ 3 } \)
RS Aggarwal Class 8 Solutions Chapter 4 Cubes and Cube Roots Ex 4D 9.1

Question 10.
Solution:
(0.8)³
= 0.8 x 0.8 x 0.8 = 0.512 (c)

Hope given RS Aggarwal Solutions Class 8 Chapter 4 Cubes and Cube Roots Ex 4D are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.