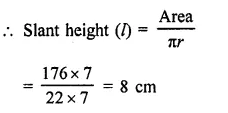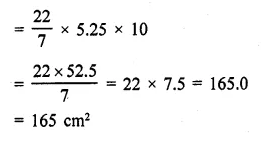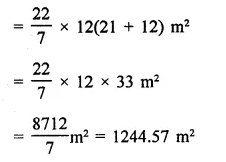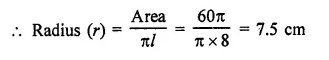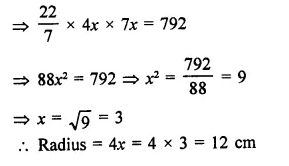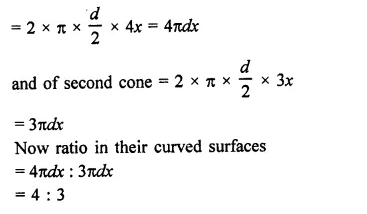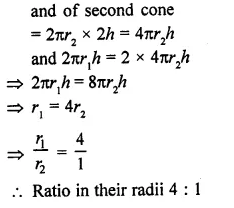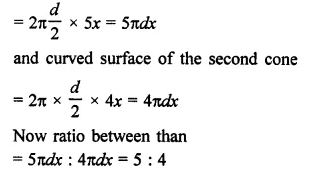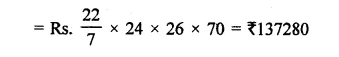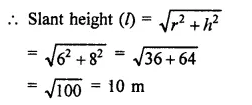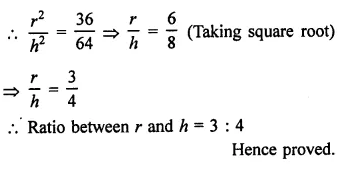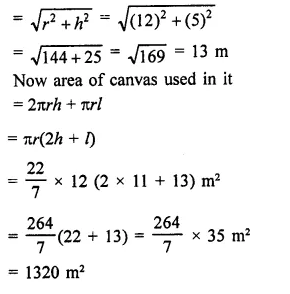Prasanna – Page 956 – MCQ Questions

RS Aggarwal Class 8 Solutions Chapter 18 Area of a Trapezium and a Polygon Ex 18B

January 5, 2022July 6, 2018 by Prasanna

RS Aggarwal Class 8 Solutions Chapter 18 Area of a Trapezium and a Polygon Ex 18B

These Solutions are part of RS Aggarwal Solutions Class 8. Here we have given RS Aggarwal Solutions Class 8 Chapter 18 Area of a Trapezium and a Polygon Ex 18B.

Other Exercises

RS Aggarwal Solutions Class 8 Chapter 18 Area of a Trapezium and a Polygon Ex 18A
RS Aggarwal Solutions Class 8 Chapter 18 Area of a Trapezium and a Polygon Ex 18B
RS Aggarwal Solutions Class 8 Chapter 18 Area of a Trapezium and a Polygon Ex 18C

Question 1.
Solution:
In quad. ABCD
AC = 24 cm, BL ⊥ AC and DM ⊥ AC
BL = 8 cm and DM = 7 cm
RS Aggarwal Class 8 Solutions Chapter 18 Area of a Trapezium and a Polygon Ex 18B 1.1

Question 2.
Solution:
In quad. ABCD, diagonal BD = 36 m
AL ⊥ BD and CM ⊥ BD
AL = 19 m and CM = 11 m
RS Aggarwal Class 8 Solutions Chapter 18 Area of a Trapezium and a Polygon Ex 18B 2.1

Question 3.
Solution:
In the given pentagon ABCDE,
BL ⊥ AC, DM ⊥ AC, EN ⊥ AC
AC = 18 cm, AM = 14 cm, AN = 6 cm,
BL = 4 cm, DM = 12 cm and EN = 9 cm
RS Aggarwal Class 8 Solutions Chapter 18 Area of a Trapezium and a Polygon Ex 18B 3.1

Question 4.
Solution:
In hexagon ABCDEF, there are triangles and trapeziums
AP = 6 cm, PL = 2 cm, LN = 8 cm,
NM = 2 cm, MD = 3 cm, FP = 8 cm,
EN = 12 cm, BL = 8 cm and CM = 6 cm
RS Aggarwal Class 8 Solutions Chapter 18 Area of a Trapezium and a Polygon Ex 18B 4.1

Question 5.
Solution:
In the given pentagon ABCDE,
BL ⊥ AC, CM ⊥ AD, EN ⊥ AD
AC = 10 cm, D = 12 cm, BL = 3 cm,
CM = 7 cm and EN = 5 cm
RS Aggarwal Class 8 Solutions Chapter 18 Area of a Trapezium and a Polygon Ex 18B 5.1

Question 6.
Solution:
In the figure, ABCF is 0 square and CDEF is a trapezium
Now area of sq. ABCF
= (side)² = (20)² = 400 cm²
area of trap. CDEF
= \(\\ \frac { 1 }{ 2 } \) (ED + FC ) x height
RS Aggarwal Class 8 Solutions Chapter 18 Area of a Trapezium and a Polygon Ex 18B 6.1

Question 7.
Solution:
In the right ∆ABC
AB² = BC² + AC²
=> (5)² = (4)² + AC²
25 = 16 + AC²
AC² = 25 – 16 = 9 = (3)²
AC = 3 cm
RS Aggarwal Class 8 Solutions Chapter 18 Area of a Trapezium and a Polygon Ex 18B 7.1
= 32 + 36
= 68 cm²

Question 8.
Solution:
AD = 23 cm, LM = 13 cm
AL = MD = \(\\ \frac { 23-13 }{ 2 } \) = \(\\ \frac { 10 }{ 2 } \) = 5 cm
RS Aggarwal Class 8 Solutions Chapter 18 Area of a Trapezium and a Polygon Ex 18B 8.1

Hope given RS Aggarwal Solutions Class 8 Chapter 18 Area of a Trapezium and a Polygon Ex 18B are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 9 Solutions Chapter 20 Surface Areas and Volume of A Right Circular Cone Ex 20.1

January 5, 2022July 6, 2018 by Prasanna

RD Sharma Class 9 Solutions Chapter 20 Surface Areas and Volume of A Right Circular Cone Ex 20.1

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 20 Surface Areas and Volume of A Right Circular Cone Ex 20.1

Other Exercises

Question 1.
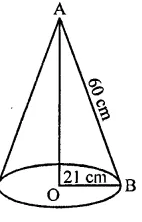
Find the curved surface area of a cone, if its slant height is 60 cm and the radius of its base is 21 cm.
Solution:
Radius of the base of the cone = 21 cm
and slant height (l) = 60 cm
RD Sharma Class 9 Solutions Chapter 20 Surface Areas and Volume of A Right Circular Cone Ex 20.1 1.1

Question 2.
The radius of a cone is 5 cm and vertical height is 12 cm. Find the area of the curved surface.
Solution:
Radius of the base of a cone = 5 cm
Vertical height (h) = 12 cm
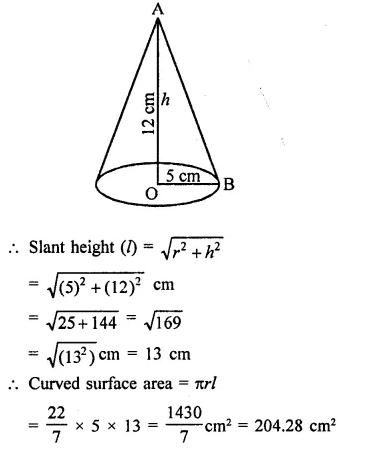
RD Sharma Class 9 Solutions Chapter 20 Surface Areas and Volume of A Right Circular Cone Ex 20.1 2.1

Question 3.
The radius of a cone is 7 cm and area of curved surface is 176 cm2. Find the slant height.
Solution:
Curved surface area of a cone = 176 cm²
and radius (r) = 1 cm²
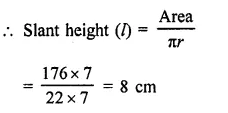
RD Sharma Class 9 Solutions Chapter 20 Surface Areas and Volume of A Right Circular Cone Ex 20.1 3.1

Question 4.
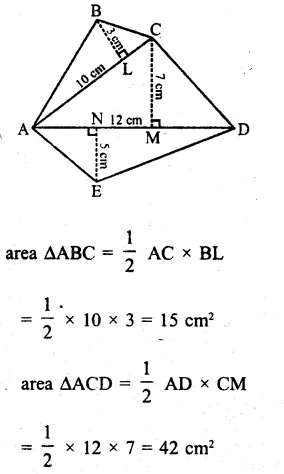
The height of a cone is 21 cm. Find the area of the base if the slant height is 28 cm.
Solution:
Height of the cone (h) = 21 cm
Slant height (l) = 28 cm
∴ l² = r² + h²
⇒ r² = l²– h² = (28)² – (21 )²
⇒ 784 – 441 = 343 …(i)
Now area of base = πr²
= \(\frac { 22 }{ 7 }\) x 343 [From (i)]
= 22 x 49 = 1078 cm²

Question 5.
Find the total surface area of a right circular cone with radius 6 cm and height 8 cm.
Solution:
Radius of base of cone (r) = 6 cm
and height (h) = 8 cm
RD Sharma Class 9 Solutions Chapter 20 Surface Areas and Volume of A Right Circular Cone Ex 20.1 5.1

Question 6.
Find the curved surface area of a cone with base radius 5.25 cm and slant height 10 cm. [NCERT]
Solution:
Radius of base of a cone (r) = 5.25 cm
and slant height (l) = 10 cm
Curved surface area = πrl
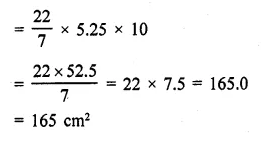
RD Sharma Class 9 Solutions Chapter 20 Surface Areas and Volume of A Right Circular Cone Ex 20.1 6.1

Question 7.
Find the total surface area of a cone, if its slant height is 21 m and diameter of its base is 24 m. [NCERT]
Solution:
Slant height of a cone (l) = 21 m
and diameter of its base = 24 m
∴ Radius (r) = \(\frac { 24 }{ 2 }\) = 12 m
Now total surface area = πr(l + r)
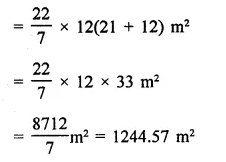
RD Sharma Class 9 Solutions Chapter 20 Surface Areas and Volume of A Right Circular Cone Ex 20.1 7.1

Question 8.
The area of the curved surface of a cone is 60π cm². If the slant height of the cone be 8 cm, find the radius of the base.
Solution:
Curved surface area of a cone = 6071 cm²
Slant height (l) = 8 cm
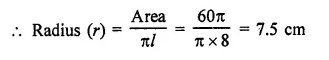
RD Sharma Class 9 Solutions Chapter 20 Surface Areas and Volume of A Right Circular Cone Ex 20.1 8.1

Question 9.
The curved surface area of a cone is 4070 cm² and its diameter is 70 cm. What is the slant height ? (Use π = 22/7).
Solution:
Surface area of a cone = 4070 cm²
Diameter of its base = 70 cm
RD Sharma Class 9 Solutions Chapter 20 Surface Areas and Volume of A Right Circular Cone Ex 20.1 9.1

Question 10.
The radius and slant height of a cone are in the ratio of 4 : 7. If its curved surface area is 792 cm², find its radius. (Use π = 22/7)
Solution:
Curved surface area of a cone = 792 cm²
Ratio in radius and slant height = 4:7
Let radius = 4x
Then slant height = 7x
∴ Curved surface area πrl = 792
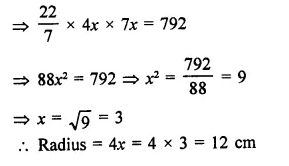
RD Sharma Class 9 Solutions Chapter 20 Surface Areas and Volume of A Right Circular Cone Ex 20.1 10.1

Question 11.
A Joker’s cap is in the form of a right circular cone of base radius 7 cm and height 24 cm. Find the area of the sheet required to make 10 such caps. [NCERT]
Solution:
Radius of the base of a conical cap (r) = 7 cm
and height (h) = 24 cm
RD Sharma Class 9 Solutions Chapter 20 Surface Areas and Volume of A Right Circular Cone Ex 20.1 11.1

Question 12.
Find the ratio of the curved surface areas of two cones if their diameters of the bases are equal and slant heights are in the ratio 4 : 3.
Solution:
Let diameters of each cone = d
Then radius (r) = \(\frac { d }{ 2 }\)
Ratio in their slant heights = 4 : 3
Let slant height of first cone = 4x
and height of second cone = 3x
Now curved surface area of the first cone = 2πrh
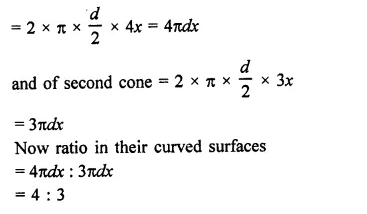
RD Sharma Class 9 Solutions Chapter 20 Surface Areas and Volume of A Right Circular Cone Ex 20.1 12.1

Question 13.
There are two cones. The curved surface area of one is twice that of the other. The slant height of the later is twice that of the former. Find the ratio of their radii.
Solution:
In two cones, curved surface of the first cone = 2 x curved surface of the second cone
Slant height of the second cone = 2 x slant height of first cone
Let r₁ and r₂ be the radii of the two cones
and let height of the first cone = h
Then height of second cone = 2h
∴ Curved surface of the first cone = 2πr₁h
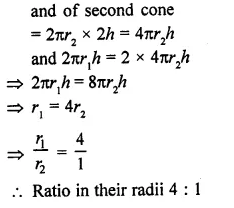
RD Sharma Class 9 Solutions Chapter 20 Surface Areas and Volume of A Right Circular Cone Ex 20.1 13.1

Question 14.
The diameters of two cones are equal. If their slant heights are in the ratio 5 : 4, find the ratio of their curved surfaces.
Solution:
Let diameter of one cone = d
and diameter of second cone = d
∴ Radius of the first cone (r) = \(\frac { d }{ 2 }\)
and of second cone (r₂) = \(\frac { d }{ 2 }\)
Ratio in their slant heights = 5:4
Let slant height of the first cone = 5x
Then that of second cone = 4x
Now curved surface of the first cone = 2πrh
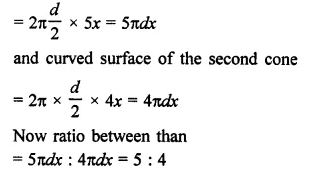
RD Sharma Class 9 Solutions Chapter 20 Surface Areas and Volume of A Right Circular Cone Ex 20.1 14.1

Question 15.
Curved surface area of a cone is 308 cm² and its slant height is 14 cm. Find the radius of the base and total surface area of the cone. [NCERT]
Solution:
Area of curved surface of a cone = 308 cm²
and slant height (l) = 14 cm
RD Sharma Class 9 Solutions Chapter 20 Surface Areas and Volume of A Right Circular Cone Ex 20.1 15.1

Question 16.
The slant height and base diameter of a conical tomb are 25 m and 14 m respectively. Find the cost of white-washing its curved surface at the rate of Rs. 210 per 100 m². [NCERT]
Solution:
Slant height of a cone (l) = 25 m
RD Sharma Class 9 Solutions Chapter 20 Surface Areas and Volume of A Right Circular Cone Ex 20.1 16.1

Question 17.
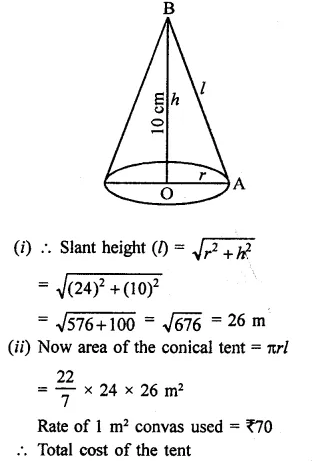
A conical tent is 10 m high and the radius of its base is 24 m. Find the slant height of the tent. If the cost of 1 m² canvas is Rs. 70, find the cost of the canvas required to make the tent. [NCERT]
Solution:
Height of conical tent (A) = 10 m
Radius of the base (r) = 24 m
RD Sharma Class 9 Solutions Chapter 20 Surface Areas and Volume of A Right Circular Cone Ex 20.1 17.1

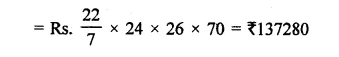
Question 18.
The circumference of the base of a 10 m height conical tent is 44 metres. Calculate the length of canvas used in making the tent if width of canvas is 2 m. (Use π = 22/7)
Solution:
Circumference of the base of a conical tent = 44 m
RD Sharma Class 9 Solutions Chapter 20 Surface Areas and Volume of A Right Circular Cone Ex 20.1 18.1

Question 19.
What length of tarpaulin 3 m wide will be required to make a conical tent of height 8 m and base radius 6 m? Assum that the extra length of material will be required for stitching margins and wastage in cutting is approximately 20 cm. (Use π = 3.14) [NCERT]
Solution:
Height of the conical tent (h) = 8 m
and radius of the base (r) = 6 m
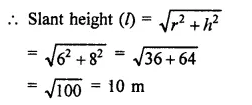
RD Sharma Class 9 Solutions Chapter 20 Surface Areas and Volume of A Right Circular Cone Ex 20.1 19.1
Now curved surface area of the tent = πrl = 3.14 x 6 x 10 = 188.4 m
Width of tarpaulin used = 3 m
∴ Length = 188.4 , 3 = 62.8 m
Extra length required = 20 cm = 0.2 m
∴ Total length of tarpaulin = 62.8 + 0.2 = 63 m

Question 20.
A bus stop is barricated from the remaining part of the road, by using 50 hollow cones made of recycled card-board. Each cone has a base diameter of 40 cm and height 1 m. If the outer side of each of the cones is to be painted and the cost of painting is ₹12 per m², what will be the cost of painting these cones. (Use π = 3.14 and \(\sqrt { 1.04 } \) = 1.02) [NCERT]
Solution:
Diameter of the base of tent = 40 cm
∴ Radius of the base of cone (r) = \(\frac { 40 }{ 2 }\)
RD Sharma Class 9 Solutions Chapter 20 Surface Areas and Volume of A Right Circular Cone Ex 20.1 20.1

Question 21.
A cylinder and a cone have equal radii of their bases and equal heights. If their curved surface areas are in the ratio 8 : 5, show that the radius of each is to the height of each as 3 : 4.
Solution:
Let radius of cylinder = r
and radius of cone = r
and let height of cylinder = h
and height of cone = h
RD Sharma Class 9 Solutions Chapter 20 Surface Areas and Volume of A Right Circular Cone Ex 20.1 21.1

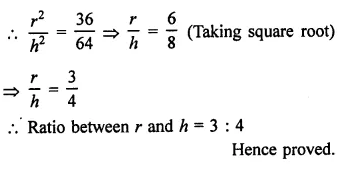
Question 22.
A tent is in the form of a right circular cylinder surmounted by a cone. The diameter of cylinder is 24 m. The height of the cylindrical portion is 11 m while the vertex of the cone is 16 m above the ground. Find the area of the canvas required for the tent.
Solution:
Diameter of the cylindrical portion = 24 m 24
∴ Radius (r) = \(\frac { 24 }{ 2 }\) = 12 m
Height of cylindrical portion = 11 m
and total height = 16 m
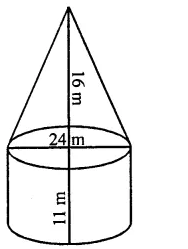
RD Sharma Class 9 Solutions Chapter 20 Surface Areas and Volume of A Right Circular Cone Ex 20.1 22.1
∴ Height of conical portion = 16 – 11 = 5 m
∴ Slant height of the conical portion (l)

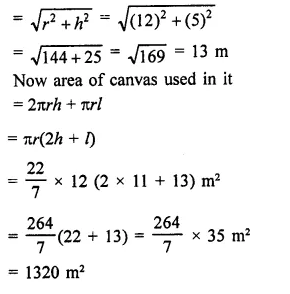
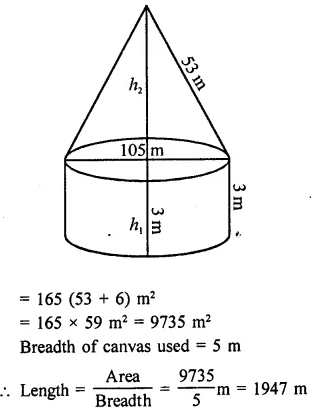
Question 23.
A circus tent is cylindrical to a height of 3 meters and conical above it. If its diameter is 105 m and the slant height of the conical portion is 53 m, calculate the length of the canvas 5 m wide to make the required tent.
Solution:
Diameter of the cylindrical tent = 105 m
RD Sharma Class 9 Solutions Chapter 20 Surface Areas and Volume of A Right Circular Cone Ex 20.1 23.1

Hope given RD Sharma Class 9 Solutions Chapter 20 Surface Areas and Volume of A Right Circular Cone Ex 20.1 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 8 Solutions Chapter 18 Area of a Trapezium and a Polygon Ex 18A

January 5, 2022July 6, 2018 by Prasanna

RS Aggarwal Class 8 Solutions Chapter 18 Area of a Trapezium and a Polygon Ex 18A

These Solutions are part of RS Aggarwal Solutions Class 8. Here we have given RS Aggarwal Solutions Class 8 Chapter 18 Area of a Trapezium and a Polygon Ex 18A.

Other Exercises

Question 1.
Solution:
In trapezium ABCD,
Length of parallel sides
AB = 24 cm, DC = 20 cm
and distance between them = 15 cm
RS Aggarwal Class 8 Solutions Chapter 18 Area of a Trapezium and a Polygon Ex 18A 1.1

Question 2.
Solution:
Parallel sides of a trapezium ABCD are
l1 = 38.7 cm. and l2 = 22.3 cm
RS Aggarwal Class 8 Solutions Chapter 18 Area of a Trapezium and a Polygon Ex 18A 2.1

Question 3.
Solution:
Parallel sides of the trapezium = 1 m, 1.4 m
RS Aggarwal Class 8 Solutions Chapter 18 Area of a Trapezium and a Polygon Ex 18A 3.1

Question 4.
Solution:
Area of trapezium = 1080 cm²
Lengths of parallel sides are
l1 = 55 cm and l2 = 35 cm
Let h be the distance between them
RS Aggarwal Class 8 Solutions Chapter 18 Area of a Trapezium and a Polygon Ex 18A 4.1

Question 5.
Solution:
Area of trapezium shaped field = 1586m²
Distance between parallel sides = 26 m
Sum of the parallel sides = \(\frac { Area\times 2 }{ Altitude }\)
= \(\frac { 1586\times 2 }{ 26 } \) = 122 m
One side = 84 m
Second side = 122 – 84
= 38 m

Question 6.
Solution:
Area of trapezium = 405 cm²
Ratio in parallel sides = 4:5
and distance between them = 18 cm
RS Aggarwal Class 8 Solutions Chapter 18 Area of a Trapezium and a Polygon Ex 18A 6.1

Question 7.
Solution:
Area of trapezium = 180 cm²
Height (h) = 9 cm.
Let l1 and l2 be the parallel sides,
RS Aggarwal Class 8 Solutions Chapter 18 Area of a Trapezium and a Polygon Ex 18A 7.1

Question 8.
Solution:
Let one of parallel sides = x
Then second sides = 2x
Area = 9450 m²
Distance between them = 84 m
RS Aggarwal Class 8 Solutions Chapter 18 Area of a Trapezium and a Polygon Ex 18A 8.1

Question 9.
Solution:
Perimeter of trapezium ABCD = 130 m
AB ⊥ AD and BC
BC = 54 m, CD = 19 m, AD = 42 m
RS Aggarwal Class 8 Solutions Chapter 18 Area of a Trapezium and a Polygon Ex 18A 9.1

Question 10.
Solution:
In the given trapezium ABCD, AC is
RS Aggarwal Class 8 Solutions Chapter 18 Area of a Trapezium and a Polygon Ex 18A 10.1

Question 11.
Solution:
In trapezium ABCD,
RS Aggarwal Class 8 Solutions Chapter 18 Area of a Trapezium and a Polygon Ex 18A 11.1

Question 12.
Solution:
In trapezium ABCD,
RS Aggarwal Class 8 Solutions Chapter 18 Area of a Trapezium and a Polygon Ex 18A 12.1
AB || DC
AB = 25 cm DC = 1 cm
AD = 13 cm and BC = 15 cm

Hope given RS Aggarwal Solutions Class 8 Chapter 18 Area of a Trapezium and a Polygon Ex 18A are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

Value Based Questions in Science for Class 9 Chapter 12 Sound

January 5, 2022July 5, 2018 by Prasanna

Value Based Questions in Science for Class 9 Chapter 12 Sound

These Solutions are part of Value Based Questions in Science for Class 9. Here we have given Value Based Questions in Science for Class 9 Chapter 12 Sound

VALUE BASED QUESTIONS

Question 1.
Mr. Ravi Bushan, father of Mr. Atul was hard of hearing. Doctor advised him to use hearing aid after diagnosing his ears. But he was not ready to listen to the advice of doctor because he felt that hearing aid is a machine and would cause harm to him. Mr. Atul told his father that hearing aid is not harmful, rather it would help him. Finally, Mr. Ravi decided to have the hearing aid.

What values are shown by Mr. Atul ?
On what principle, hearing aid works ?

Answer:

1. Concern for his father and
2. high degree of general awareness.
Hearing aid works on the principle of multiple relfection of sound.

More Resources

Question 2.
Ajay’s uncle was advised by his doctor to have echocardiography. His uncle did not know anything regarding the echocardiography. He thought that this test is sensitive and hence he was not ready for it. When Ajay came to know about this, he decided to prepare his uncle for the test. He told his uncle that this test would help the doctor to know the condition of his heart and moreover, this test is very simple. Finally his uncle was convinced and had the echocardiography. The information obtained by the test helped his doctor to treat him well.

What is echocardiography ?
What values are shown by Ajay ?

Answer:

Echocardiography is medical diagnostic technique to construct the image of heart using ultrasonice waves.
1. Helpful,
2. concern for his uncle, and
3. high degree of general awareness.

Question 3.
Harsha was watching a programme based on ships on television. She saw a device attached to a ship through which the man on the ship located the enemy submarines and sent the message to the headquarters.

Name the device fitted in the ship.
On which principle does the device work ?
What values are shown by Harsha ? (CBSE 2015)

Answer:

SONAR
SONAR works on the principle of reflection of sound waves (i.e. echo).
Harsha is inquisitive. She has scientific temperament and takes interest in understanding scientific phenomena.

Question 4.
David while watching ‘National Geographic’ channel on television observed that Bats were easily flying during the night. He did not understand the concept and for this he surfed on internet, and finally found the answer that bats use ultrasound to fly and search their prey at night.

What is ultrasound ? State its one application.
State the principle used by bats.
What value of David’s Nature is depicted from this context ? (CBSE 2015)

Answer:

The sound waves having frequency greater than 20000 Hz are called ultrasound. Ultrasound is used to
determine the depth of a sea.
Bats use the principle of reflection of ultrasound (i.e. echo).
David is inquisitive. He has scientific temperament and takes interest in understanding the natural phenomena.

Hope given Value Based Questions in Science for Class 9 Chapter 12 Sound are helpful to complete your science homework.

If you have any doubts, please comment below. Learn Insta try to provide online science tutoring for you.

HOTS Questions for Class 9 Science Chapter 12 Sound

January 5, 2022July 5, 2018 by Prasanna

HOTS Questions for Class 9 Science Chapter 12 Sound

These Solutions are part of HOTS Questions for Class 9 Science. Here we have given HOTS Questions for Class 9 Science Chapter 12 Sound

Question 1.
Sound of explosions taking place on other planets are not heard by a person on the earth. Explain, why ?
(CBSE 2011)
Answer:
Sound needs material medium for its propagation from one place to another place. In other words, sound cannot travel through vacuum. Since there is a region in between the planets and the earth, where there is a vacuum, so the sound of explosions taking place on other planets cannot pass through this vaccum. Hence cannot reach the earth.

More Resources

Question 2.
Two astronauts on the surface of the moon cannot talk to each other. Explain, why ?
Answer:
Since there is no atmosphere on the surface of the moon (i.e. no medium for the propagation of sound), so the sound cannot travel from one astronaut to another astronaut on the surface of the moon.

Question 3.
A loud sound can be heard at a large distance but a feeble or soft sound cannot be heard at a large distance. Explain, why ?
Answer:
Sound is a form of energy which is transferred from one place to another place. As sound energy is directly proportional to the square of the amplitude of a vibrating body, so loud sound has large energy, whereas soft sound has small energy. As the sound travels through a medium, sound with small energy is absorbed after travelling a small distance in the medium but sound with large energy will be absorbed after travelling a large distance in the medium. Therefore, loud sound can be heard at a large distance but feeble sound cannot be heard at a large distance.

Question 4.
A sound wave travelling in a medium is represented as shown in figure,

Which letter represents the amplitude of the sound wave ?
Which letter represents the wavelength of the wave ?
What is the frequency of the source of sound if the vibrating source of sound makes 360 oscillations in 2 minutes ?

Answer:

Letter X represents the amplitude of the sound wave.
Letter Y represents the wavelength of the sound wave.
Number of oscillations made in 2 minutes (120 s) = 360

Hence, frequency of the source of sound = 3 Hz

Question 5.
Represent the following sound waves,
(i) Waves having same amplitude but different frequencies
(ii) Waves having same frequency but different amplitudes
(iii) Waves having different amplitudes and different wave lengths.
(CBSE 2011, 2012)
Answer:
HOTS Questions for Class 9 Science Chapter 12 Sound image - 3

Question 6.
An echo is heard on a day when temperature is about 22° C. Will the echo be heard sooner or later if the temperature falls to 4°C ? (Similar CBSE 2014)
Distance
Answer:
HOTS Questions for Class 9 Science Chapter 12 Sound image - 4
Since, speed of sound in air decreases with the decrease in temperature, so the time after which the echo will be heard increases. Hence, the echo will be heard later than the echo heard when temperature was 22° C.

Question 7.
An echo is heard on a day when temperature is about 22° C. Will the echo be heard sooner or later if the temperature increases to 40° C ? (Similar CBSE 2014)
Answer:
HOTS Questions for Class 9 Science Chapter 12 Sound image - 5
Since, speed of sound in air increases with the increase in temperature, so the time after which the echo will be heard decreases. Hence, echo will be heard sooner than the echo heard when temperature was 22° C.

Question 8.
When we put our ear on a railway track, we can hear the sound of an approaching train even when the train is not visible but its sound cannot be heard through air. Why ? (CBSE 2015, 2016)
Answer:
Sound travels faster in solids than in gases. Therefore, we can hear the sound of an approaching train by putting our ear on a railway track even when the train is not visible.

Hope given HOTS Questions for Class 9 Science Chapter 12 Sound are helpful to complete your science homework.

If you have any doubts, please comment below. Learn Insta try to provide online science tutoring for you.