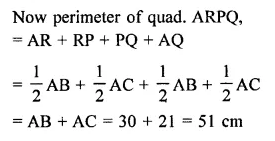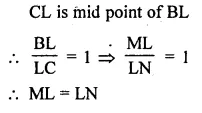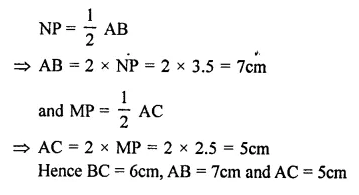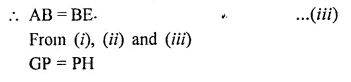RD Sharma Class 9 Solutions Chapter 13 Linear Equations in Two Variables Ex 13.4
These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 13 Linear Equations in Two Variables Ex 13.4
Other Exercises
Question 1.
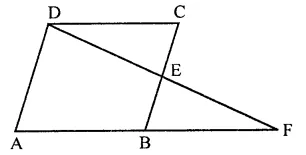
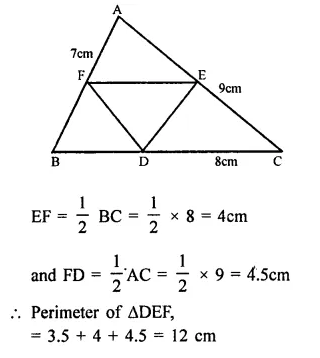
In a ∆ABC, D, E and F are respectively, the mid-points of BC, CA and AB. If the lengths of side AB, BC and CA are 7cm, 8cm and 9cm, respectively, find the perimeter of ∆DEF.
Solution:
In ∆ABC, D, E and F are the mid-points of sides,
BC, CA, AB respectively
AB = 7cm, BC = 8cm and CA = 9cm
∵ D and E are the mid points of BC and CA
∴ DE || AB and DE =\(\frac { 1 }{ 2 }\) AB =\(\frac { 1 }{ 2 }\) x 7 = 3.5cm
Similarly,
Question 2.
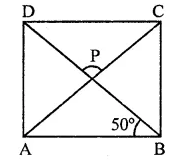
In a triangle ∠ABC, ∠A = 50°, ∠B = 60° and ∠C = 70°. Find the measures of the angles of the triangle formed by joining the mid-points of the sides of this triangle.
Solution:
In ∆ABC,
∠A = 50°, ∠B = 60° and ∠C = 70°
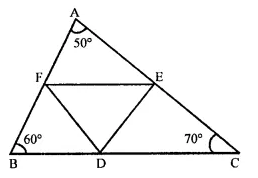
D, E and F are the mid points of sides BC, CA and AB respectively
DE, EF and ED are joined
∵ D, E and F are the mid points of sides BC, CA and AB respectively
∴ EF || BC
DE || AB and FD || AC
∴ BDEF and CDEF are parallelogram
∴ ∠B = ∠E = 60° and ∠C = ∠F = 70°
Then ∠A = ∠D = 50°
Hence ∠D = 50°, ∠E = 60° and ∠F = 70°
Question 3.
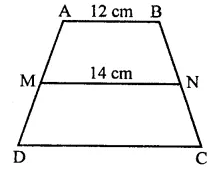
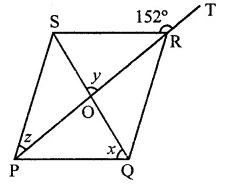
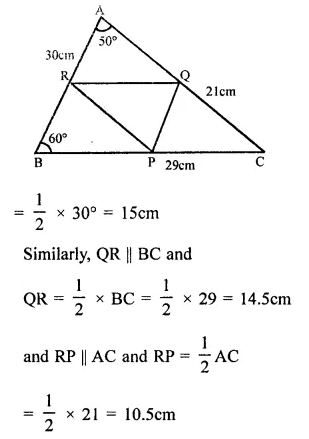
In a triangle, P, Q and R are the mid-points of sides BC, CA and AB respectively. If AC = 21 cm, BC = 29cm and AB = 30cm, find the perimeter of the quadrilateral ARPQ.
Solution:
P, Q, R are the mid points of sides BC, CA and AB respectively
AC = 21 cm, BC = 29 cm and AB = 30°
∵ P, Q, R and the mid points of sides BC, CA and AB respectively.
∴ PQ || AB and PQ = \(\frac { 1 }{ 2 }\) AB
Question 4.
In a ∆ABC median AD is produced to X such that AD = DX. Prove that ABXC is a parallelogram.
Solution:
Given : In ∆ABC, AD is median and AD is produced to X such that DX = AD
To prove : ABXC is a parallelogram
Construction : Join BX and CX
Proof : In ∆ABD and ∆CDX
AD = DX (Given)
BD = DC (D is mid points)
∠ADB = ∠CDX (Vertically opposite angles)
∴ ∆ABD ≅ ∆CDX (SAS criterian)
∴ AB = CX (c.p.c.t.)
and ∠ABD = ∠DCX
But these are alternate angles
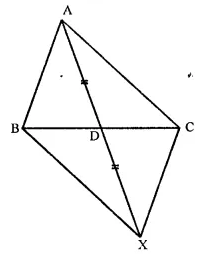
∴ AB || CX and AB = CX
∴ ABXC is a parallelogram.
Question 5.
In a ∆ABC, E and F are the mid-points of AC and AB respectively. The altitude AP to BC intersects FE at Q. Prove that AQ = QP.
Solution:
Given : In ∆ABC, E and F are the mid-points of AC and AB respectively.
EF are joined.
AP ⊥ BC is drawn which intersects EF at Q and meets BC at P.
To prove: AQ = QP
proof : In ∆ABC
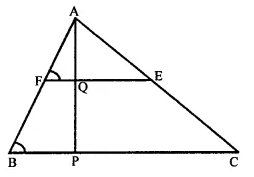
E and F are the mid points of AC and AB
∴ EF || BC and EF = \(\frac { 1 }{ 2 }\)BC
∴ ∠F = ∠B
In ∆ABP,
F is mid point of AB and Q is the mid point of FE or FQ || BC
∴ Q is mid point of AP,
∴ AQ = QP
Question 6.
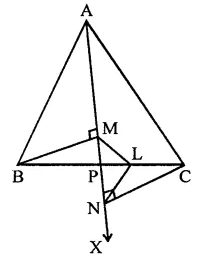
In a ∆ABC, BM and CN are perpendiculars from B and C respectively on any line passing through A. If L is the mid-point of BC, prove that ML NL.
Solution:
In ∆ABC,
BM and CN are perpendicular on a line drawn from A. L is the mid point of BC. ML and NL are joined.

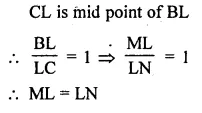
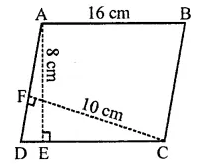
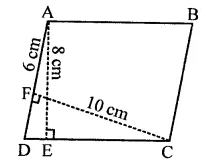
Question 7.
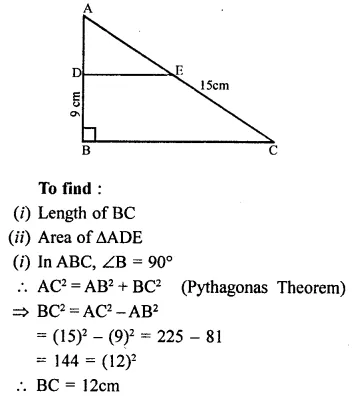
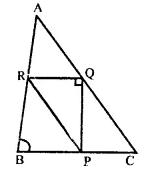
In the figure triangle ABC is right-angled at B. Given that AB = 9cm. AC = 15cm and D, E are the mid points of the sides AB and AC respectively, calculate.
(i) The length of BC
(ii) The area of ∆ADC
Solution:
In ∆ABC, ∠B = 90°
AC =15 cm, AB = 9cm
D and E are the mid points of sides AB and AC respectively and D, E are joined.

Question 8.
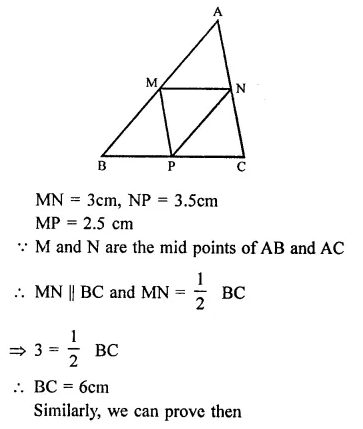
In the figure, M, N and P are the mid points of AB, AC and BC respectively. If MN = 3 cm, NP = 3.5cm and MP = 2.5cm, calculate BC, AB and AC.
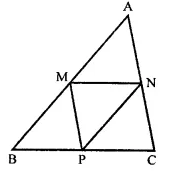
Solution:
In ∆ABC,
M, N and P are the mid points of side, AB, AC and BC respectively.
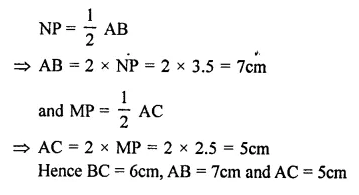
Question 9.
In the figure, AB = AC and CP || BA and AP is the bisector of exterior ∠CAD of ∆ABC. Prove that (i) ∠PAC = ∠BCA (ii) ABCP is a parallelogram.
Solution:
Given : In ABC, AB = AC
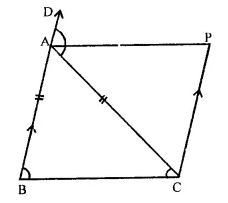
nd CP || BA, AP is the bisector of exterior ∠CAD of ∆ABC
To prove :
(i) ∠PAC = ∠BCA
(ii) ABCP is a ||gm
Proof : (i) In ∆ABC,
∵ AB =AC
∴ ∠C = ∠B (Angles opposite to equal sides) and ext.
∠CAD = ∠B + ∠C
= ∠C + ∠C = 2∠C ….(i)
∵ AP is the bisector of ∠CAD
∴ 2∠PAC = ∠CAD …(ii)
From (i) and (ii)
∠C = 2∠PAC
∠C = ∠CAD or ∠BCA = ∠PAC
Hence ∠PAC = ∠BCA
(ii) But there are alternate angles,
∴ AD || BC
But BA || CP
∴ ABCP is a ||gm.
Question 10.
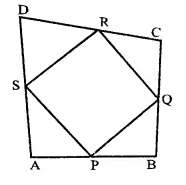
ABCD is a kite having AB = AD and BC = CD. Prove that the figure formed by joining the mid-points of the sides, in order, is a rectangle.
Solution:
Given : In fne figure, ABCD is a kite in which AB = AD and BC = CD.
P, Q, R and S are the mid points of the sides AB, BC, CD and DA respectively.
To prove : PQRS is a rectangle.
Construction : Join AC and BD.
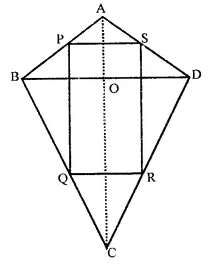
Proof: In ∆ABD,
P and S are mid points of AB and AD
∴ PS || BD and PS = \(\frac { 1 }{ 2 }\) BD …(i)
Similarly in ∆BCD,
Q and R the mid points of BC and CD
∴ QR || BD and
QR = \(\frac { 1 }{ 2 }\) BD …(ii)
∴ Similarly, we can prove that PQ || SR and PQ = SR …(iii)
From (i) and (ii) and (iii)
PQRS is a parallelogram,
∵ AC and BD intersect each other at right angles.
∴ PQRS is a rectangle.
Question 11.
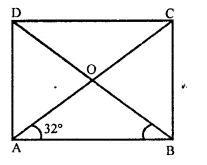
Let ABC be an isosceles triangle in which AB = AC. If D, E, F be the mid-points of the sides BC, CA and AB respectively, show that the segment AD and EF bisect each other at right angles.
Solution:
In ∆ABC, AB = AC
D, E and F are the mid points of the sides BC, CA and AB respectively,
AD and EF are joined intersecting at O
To prove : AD and EF bisect each other at right angles.
Construction : Join DE and DF.
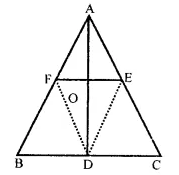
Proof : ∵ D, E and F are the mid-points of
the sides BC, CA and AB respectively
∴ AFDE is a ||gm
∴ AF = DE and AE = DF
But AF = AE
(∵ E and F are mid-points of equal sides AB and AC)
∴ AF = DF = DE = AE
∴AFDE is a rhombus
∵ The diagonals of a rhombus bisect each other at right angle.
∴ AO = OD and EO = OF
Hence, AD and EF bisect each other at right angles.
Question 12.
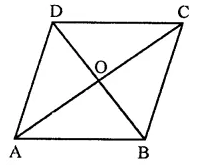
Show that the line segments joining the mid points of the opposite sides of a quadrilateral bisect each other.
Solution:
Given : In quad. ABCD,
P, Q, R and S are the mid points of sides AB, BC, CD and DA respectively.
PR and QS to intersect each other at O
To prove : PO = OR and QO = OS
Construction: Join PQ, QR, RS and SP and also join AC.
Proof: In ∆ABC
P and Q are mid-points of AB and BC
∴ PQ || AC and PQ = \(\frac { 1 }{ 2 }\) AC …(i)
Similarly is ∆ADC,
S and R are the mid-points of AD and CD
∴ SR || AC and SR = \(\frac { 1 }{ 2 }\) AC ..(ii)
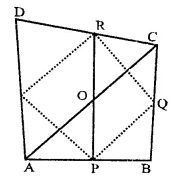
from (i) and (ii)
PQ = SQ and PQ || SR
PQRS is a ||gm (∵ opposite sides are equal area parallel)
But the diagonals of a ||gm bisect each other.
∴ PR and QS bisect each other.
Question 13.
Fill in the blanks to make the following statements correct :
(i) The triangle formed by joining the mid-points of the sides of an isosceles triangle is …
(ii) The triangle formed by joining the mid-points of the sides of a right triangle is …
(iii) The figure formed by joining the mid-points of consecutive sides of a quadrilateral is …
Solution:
(i) The triangle formed by joining the mid-points of the sides of an isosceles triangle is an isosceles triangle.
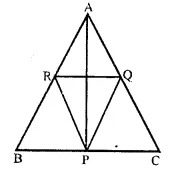
(ii) The triangle formed by joining the mid-points of the sides of a right triangle is right triangle.
(iii) The figure formed by joining the mid-points of consecutive sides of a quadrilateral is a parallelogram.
Question 14.
ABC is a triangle and through A, B, C lines are drawn parallel to BC, CA and AB respectively intersecting at P, Q and R. Prove that the perimeter of ∆PQR is double the perimeter of ∆ABC.
Solution:
Given : In ∆ABC,
Through A, B and C, lines are drawn parallel to BC, CA and AB respectively meeting at P, Q and R.
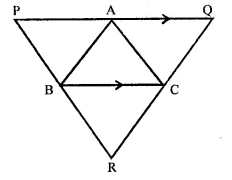
To prove : Perimeter of ∆PQR = 2 x perimeter of ∆ABC
Proof : ∵ PQ || BC and QR || AB
∴ ABCQ is a ||gm
∴ BC = AQ
Similarly, BCAP is a ||gm
∴ BC = AP …(i)
∴ AQ = AP = BL
⇒ PQ = 2BC
Similarly, we can prove that
QR = 2AB and PR = 2AC
Now perimeter of ∆PQR.
= PQ + QR + PR = 2AB + 2BC + 2AC
= 2(AB + BC + AC)
= 2 perimeter of ∆ABC.
Hence proved
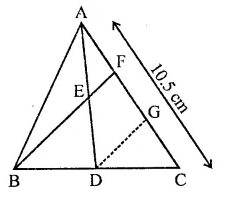
Question 15.
In the figure, BE ⊥ AC. AD is any line from A to BC intersecting BE in H. P, Q and R are respectively the mid-points of AH, AB and BC. Prove that PQR = 90°.
Solution:
Given: In ∆ABC, BE ⊥ AC
AD is any line from A to BC meeting BC in D and intersecting BE in H. P, Q and R are respectively mid points of AH, AB and BC. PQ and QR are joined B.
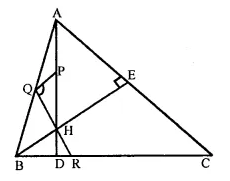
To prove : ∠PQR = 90°
Proof: In ∆ABC,
Q and R the mid points of AB and BC 1
∴ QR || AC and QR = \(\frac { 1 }{ 2 }\) AC
Similarly, in ∆ABH,
Q and P are the mid points of AB and AH
∴ QP || BH or QP || BE
But AC ⊥ BE
∴ QP ⊥ QR
∴ ∠PQR = 90°
Question 16.
ABC is a triangle. D is a point on AB such that AD = \(\frac { 1 }{ 4 }\) AB and E is a point on AC such that AE = \(\frac { 1 }{ 4 }\) AC. Prove that DE = \(\frac { 1 }{ 4 }\) BC.
Solution:
Given : In ∆ABC,
D is a point on AB such that
AD = \(\frac { 1 }{ 4 }\) AB and E is a point on AC such 1
that AE = \(\frac { 1 }{ 4 }\) AC
DE is joined.
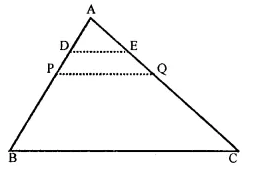
To prove : DE = \(\frac { 1 }{ 4 }\) BC
Construction : Take P and Q the mid points of AB and AC and join them
Proof: In ∆ABC,
∵ P and Q are the mid-points of AB and AC

Question 17.
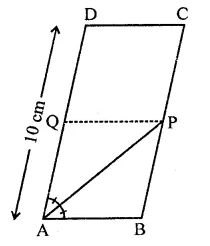
In the figure, ABCD is a parallelogram in which P is the mid-point of DC and Q is a point on AC such that CQ = \(\frac { 1 }{ 4 }\) AC. If PQ produced meets BC at R, prove that R is a mid-point of BC.
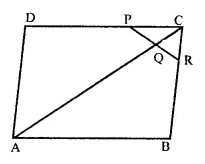
Solution:
Given : In ||gm ABCD,
P is the mid-point of DC and Q is a point on AC such that CQ = \(\frac { 1 }{ 4 }\) AC. PQ is produced meets BC at R.
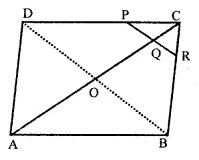
To prove : R is mid point of BC
Construction : Join BD
Proof : ∵ In ||gm ABCD,
∵ Diagonal AC and BD bisect each other at O
∴ AO = OC = \(\frac { 1 }{ 2 }\) AC …(i)
In ∆OCD,
P and Q the mid-points of CD and CO
∴ PQ || OD and PQ = \(\frac { 1 }{ 2 }\) OD
In ∆BCD,
P is mid-poiht of DC and PQ || OD (Proved above)
Or PR || BD
∴ R is mid-point BC.
Question 18.
In the figure, ABCD and PQRC are rectangles and Q is the mid-point of AC.
Prove that (i) DP = PC (ii) PR = \(\frac { 1 }{ 2 }\) AC.
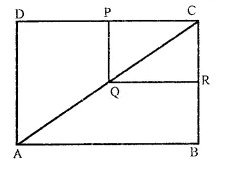
Solution:
Given : ABCD are PQRC are rectangles and Q is the mid-point of AC.
To prove : (i) DP = PC (ii) PR = \(\frac { 1 }{ 2 }\) AC
Construction : Join diagonal AC which passes through Q and join PR.
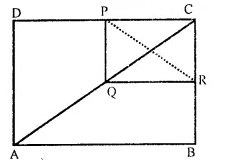
Proof : (i) In ∆ACD,
Q is mid-point of AC and QP || AD (Sides of rectangles)
∴ P is mid-point of CD
∴ DP = PC
(ii) ∵PR and QC are the diagonals of rectangle PQRC
∴ PR = QC
But Q is the mid-point of AC
∴ QC = \(\frac { 1 }{ 2 }\) AC
Hence PR = \(\frac { 1 }{ 2 }\) AC
Question 19.
ABCD is a parallelogram, E and F are the mid points AB and CD respectively. GFI is any line intersecting AD, EF and BC at Q P and H respectively. Prove that GP = PH.
Solution:
Given : In ||gm ABCD,
E and F are mid-points of AB and CD
GH is any line intersecting AD, EF and BC at GP and H respectively
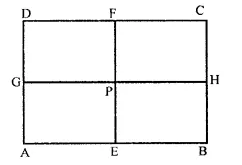
To prove : GP = PH
Proof: ∵ E and F are the mid-points of AB and CD

Question 20.
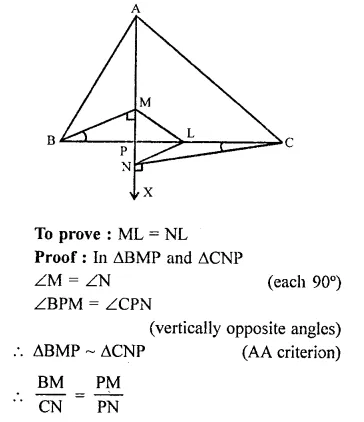
BM and CN are perpendiculars to a line passing, through the vertex A of a triangle ABC. If L is the mid-point of BC, prove that LM = LN.
Solution:
In ∆ABC,
BM and CN are perpendicular on a line drawn from A.
L is the mid point of BC.
ML and NL are joined.

Hope given RD Sharma Class 9 Solutions Chapter 13 Linear Equations in Two Variables Ex 13.4 are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.