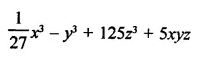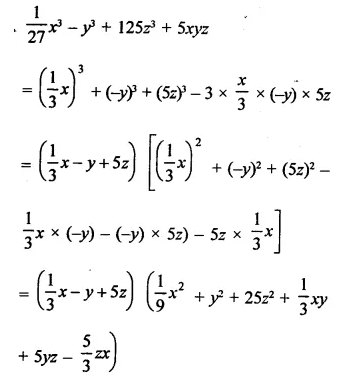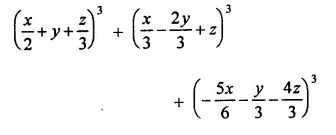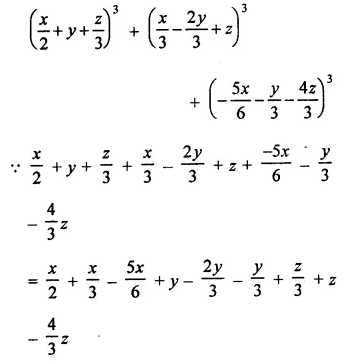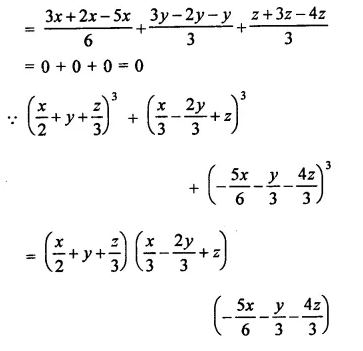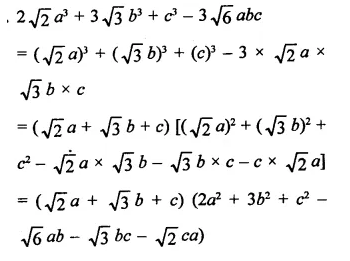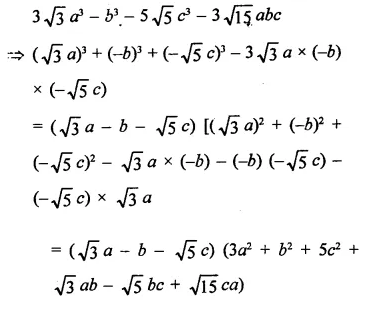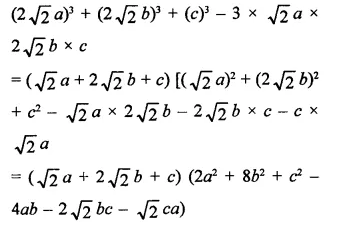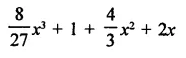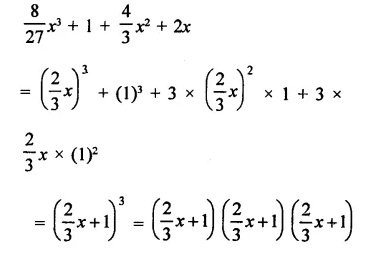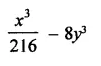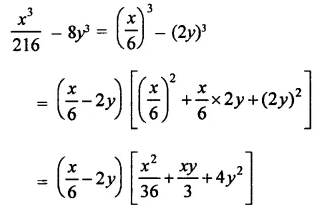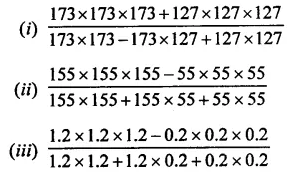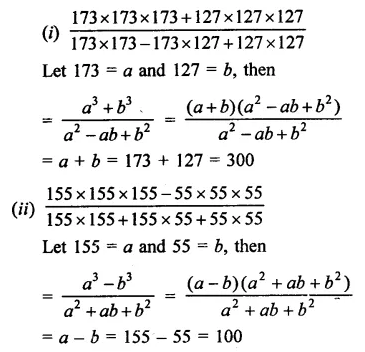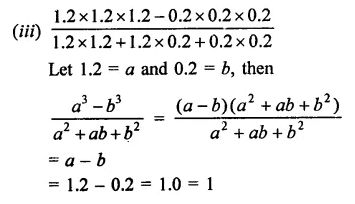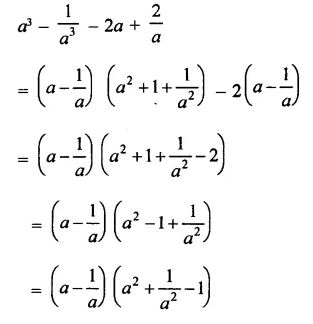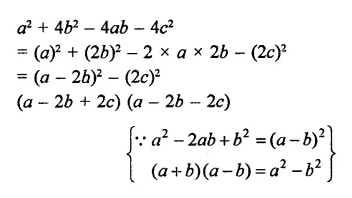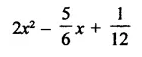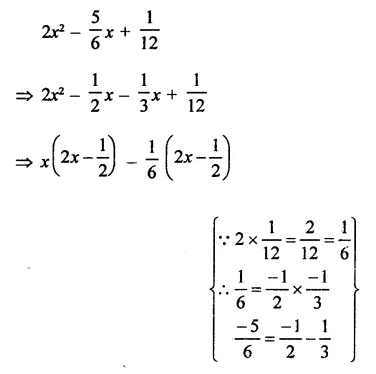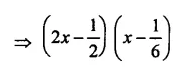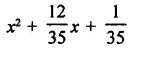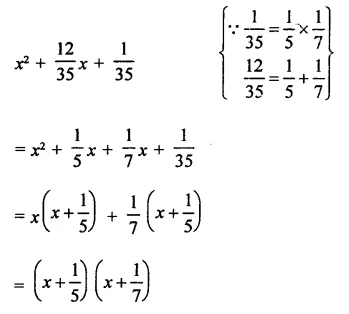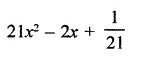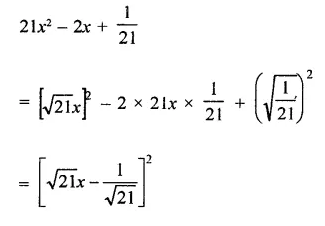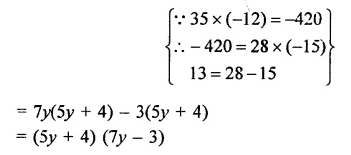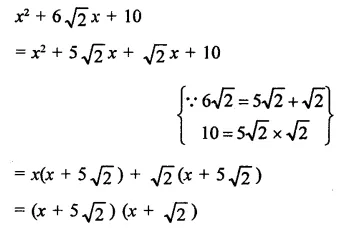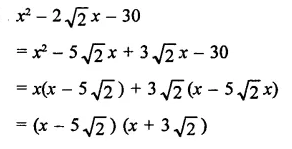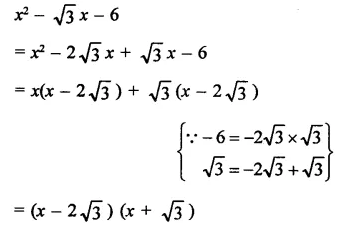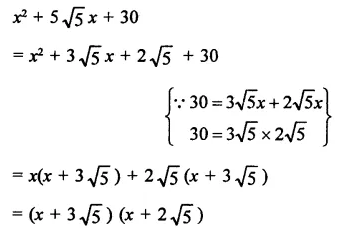RD Sharma Class 9 Maths Solutions

RD Sharma Class 9 Solutions Chapter 5 Factorisation of Algebraic Expressions MCQS

by

RD Sharma Class 9 Solutions Chapter 5 Factorisation of Algebraic Expressions MCQS

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 5 Factorisation of Algebraic Expressions MCQS

Other Exercises

Mark the correct alternative in each of the following:
Question 1.
The factors of x3 – x2y -xy2 + y3 are
(a) (x + y) (x2 -xy + y2)
(b) (x+y)(x2 + xy + y2)
(c) (x + y)2 (x – y)
(d) (x – y)2 (x + y)
Solution:
x3 – x2y – xy2 + y3
= x3 + y3 – x2y – xy2
= (x + y) (x2 -xy + y2)- xy(x + y)
= (x + y) (x2 – xy + y2 – xy)
= (x + y) (x2 – 2xy + y2)
= (x + y) (x – y)2         (d)

Question 2.
The factors of x3 – 1 +y3 + 3xy are
(a) (x – 1 + y)  (x2 + 1 + y2 + x + y – xy)
(b) (x + y + 1)  (x2 + y2 + 1- xy – x – y)
(c) (x – 1 + y)   (x2 – 1 – y2 + x + y + xy)
(d) 3(x + y – 1) (x2 + y2 – 1)
Solution:
x3 – 1 + y3 + 3xy
= (x)3 + (-1)3 + (y)3 – 3 x  x  x (-1) x y
= (x – 1 + y) (x2 + 1 + y2 + x + y – xy)
= (x- 1 + y) (x2+ 1 + y2 + x + y – xy)      (a)

Question 3.
The factors of 8a3 + b3 – 6ab + 1 are
(a) (2a + b – 1) (4a2 + b2 + 1 – 3ab – 2a)
(b) (2a – b + 1) (4a2 + b2 – 4ab + 1 – 2a + b)
(c) (2a + b+1) (4a2 + b2 + 1 – 2ab – b – 2a)
(d) (2a – 1 + b)(4a2 + 1 – 4a – b – 2ab)
Solution:
8a3 + b3 – 6ab + 1
= (2a)3 + (b)3 + (1)3 – 3 x 2a x b x 1
= (2a + b + 1) [(2a)2 + b2+1-2a x b- b x 1 – 1 x 2a]
= (2a + b + 1) (4a2 + b2+1-2ab-b- 2a)            (c)

Question 4.
(x + y)3 – (x – v)3 can be factorized as
(a) 2y (3x2 + y2)                
(b) 2x (3x2 + y2)
(c) 2y (3y2 + x2)                
(d) 2x (x2 + 3y2)
Solution:
(x + y)3 – (x – y)3
= (x + y -x + y) [(x + y)2 + (x +y) (x -y) + (x – y)2]
= 2y(x2 + y2 + 2xy + x2-y2 + x2+y2 – 2xy)
= 2y(3x2 + y2)          (a)

Question 5.
The expression (a – b)3 + (b – c)3 + (c – a)3 can be factorized as
(a) (a -b) (b- c) (c – a) 
(b) 3(a – b) (b – c) (c – a)
(c) -3(a – b) (b – c) (a – a)
(d) (a + b + c) (a2 + b2 + c2 – ab – bc – ca)
Solution:
(a – b)3 + (b – c)3 + (c – a)3
Let a – b = x, b – a = y, c – a = z
∴ x3 + y3 + z3
x+y + z = a- b + b- c + c – a = 0
∴ x3 +y3 + z3 = 3xyz
(a – b)3 + (b – a)3 + (c – a)3
= 3 (a – b) (b – c) (c – a)        (b)

Question 6.
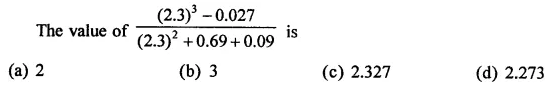
RD Sharma Class 9 Solutions Chapter 5 Factorisation of Algebraic Expressions MCQS Q6.1
Solution:
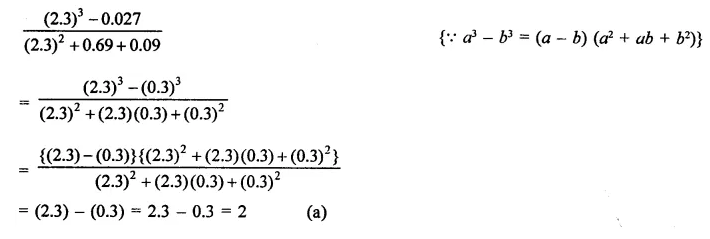
RD Sharma Class 9 Solutions Chapter 5 Factorisation of Algebraic Expressions MCQS Q6.2

Question 7.
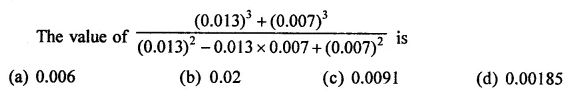
RD Sharma Class 9 Solutions Chapter 5 Factorisation of Algebraic Expressions MCQS Q7.1
Solution:
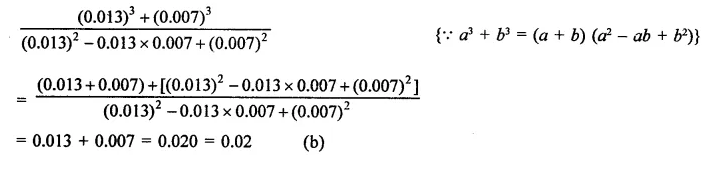
RD Sharma Class 9 Solutions Chapter 5 Factorisation of Algebraic Expressions MCQS Q7.2

Question 8.
The factors of a2 – 1 – 2x – x2 are
(a) (a – x + 1) (a – x – 1)                                
(b) (a + x – 1) (a – x + 1)
(c) (a + x + 1) (a – x – 1)                               
(d) none of these
Solution:
a2 – 1- 2x – x2
⇒ a2 – (1 + 2x + x2)
= (a)2 – (1 + x)2
= (a + 1 + x) (a – 1 – x)                         (c)

Question 9.
The factors of x4 + x2 + 25 are
(a) (x2 + 3x + 5) (x2 – 3x + 5)                      
(b) (x2 + 3x + 5) (x2 + 3x – 5)
(c) (x2 + x + 5) (x2 – x + 5)                           
(d) none of these
Solution:
x4 + x2 + 25 = x4 + 25 +x2
= (x2)2 + (5)2 + 2 x x2 x 5- 9x2
= (x2 + 5)2 – (3x)2
= (x2 + 5 + 3x) (x2 + 5 – 3x)
= (x2 + 3x + 5) (x2 – 3x + 5)                 (a)

Question 10.
The factors of x2 + 4y2 + 4y – 4xy – 2x – 8 are
(a) (x – 2y – 4) (x – 2y + 2)                            
(b)  (x – y  +   2) (x – 4y – 4)
(c) (x + 2y – 4) (x + 2y + 2)                         
(d)    none of these
Solution:
x2 + 4y2 + 4y – 4xy – 2x – 8
⇒  x2 + 4y + 4y – 4xy – 2x – 8
= (x)2 + (2y)2– 2 x x x 2y + 4y-2x-8
= (x – 2y)2 – (2x – 4y) – 8
= (x – 2y)2 – 2 (x – 2y) – 8
Let x – 2y = a, then
a2– 2a – 8 = a2– 4a + 2a – 8
= a(a – 4) + 2(a – 4)
= (a-4) (a + 2)
= (x2 -2y-4) (x2 -2y + 2)                       (a)

Question 11.
The factors of x3 – 7x + 6 are
(a) x(x – 6) (x – 1)                                           
(b) (x2 – 6) (x – 1)
(c) (x + 1) (x + 2) (x – 3)                               
(d) (x – 1) (x + 3) (x – 2)
Solution:
x3 -7x + 6= x3-1-7x + 7
= (x – 1) (x2 + x + 1) – 7(x – 1)
= (x – 1) (x2 + x + 1 – 7)
= (x – 1) (x2 + x – 6)
= (x – 1) [x2 + 3x – 2x – 6]
= (x – 1) [x(x + 3) – 2(x + 3)]
= (x – 1) (x+ 3) (x – 2)                           (d)

Question 12.
The expression x4 + 4 can be factorized as
(a) (x2 + 2x + 2) (x2 – 2x + 2)                       
(b) (x2 + 2x + 2) (x2 + 2x – 2)
(c) (x2 – 2x – 2) (x2 – 2x + 2)                         
(d) (x2 + 2) (x2 – 2)
Solution:
x4 + 4 = x4 + 4 + 4x2 – 4x2                (Adding and subtracting 4x2)
= (x2)2 + (2)2 + 2 x x2 x 2 – (2x)2
= (x2 + 2)2 – (2x)2
= (x2 + 2 + 2x) (x2 + 2 – 2x)                {∵ a2 – b2 = (a + b) (a – b)}
= (x2 + 2x + 2) (x2 – 2x + 2)                  (a)

Question 13.
If 3x = a + b + c, then the value of (x – a)3 + (x –    bf + (x – cf – 3(x – a) (x – b) (x – c) is
(a) a + b + c                                                
(b) (a – b) {b – c) (c – a)
(c) 0                                                                  
(d) none of these
Solution:
3x = a + b + c                                                                      .
⇒ 3x-a-b-c = 0
Now, (x – a)3+ (x – b)3 + (x – c)3 – 3(x – a) (x -b)  (x – c)
= {(x – a) + (x – b) + (x – c)} {(x – a)2 + (x – b)2 + (x – c)2  – (x – a) (x – b) (x – b) (x – c) – (x – c) (x – a)}
= (x – a + x – b + x – c) {(x – a)2 + (x – b)2  + (x – c)2 – (x – a) (x – b) – (x – b) (x – c) – (x – c) (x – a)}
= (3x – a – b -c) {(x – a)2 + (x -b)2+ (x – c)2 – (x – a) (x – b) – (x – b) (x – c) – (x – c) (x – a)}
But 3x-a-b-c = 0, then
= 0 x {(x – a)2 + (x – b)2 + (x – c)2 – (x – a) (x – b) – (x – b) (x – c) – (x – c) (x – a)}
= 0                                                         (c)

Question 14.
If (x + y)3 – (x – y)3 – 6y(x2 – y2) = ky2, then k =
(a) 1                                   
(b) 2                                
(c) 4                                     
(d) 8
Solution:
(x + y)3 – (x – y)3 – 6y(x2 – y2) = ky2
LHS = (x + y)3 – (x – y)3 – 3 x (x + y) (x – y) [x + y – x + y]
= (x+y-x + y)3       {∵ a3 – b3 – 3ab (a – b) = a3 – b3}
= (2y)3 = 8y3
Comparing with ky3, k = 8                     (d)

Question 15.
If x3 – 3x2 + 3x – 7 = (x + 1) (ax2 + bx + c), then a + b + c =
(a) 4                                   
(b) 12                             
(c) -10                                 
(d) 3
Solution:
x3 – 3x2 + 3x + 7 = (x + 1) (ax2 + bx + c)
= ax3 + bx2 + cx + ax2 + bx + c
x3 – 3x2 + 3x – 7 = ax3 + (b + a)2 + (c + b)x + c
Comparing the coefficient,
a = 1
b + a = -3 ⇒ b+1=-3 ⇒ b = -3-1=-4
c + b = 3 ⇒ c- 4 = 3 ⇒ c = 3 + 4 = 7
a + b + c = 1- 4 + 7 = 8- 4 = 4             (a)

Hope given RD Sharma Class 9 Solutions Chapter 5 Factorisation of Algebraic Expressions MCQS are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 9 Solutions Chapter 5 Factorisation of Algebraic Expressions Ex 5.4

by

RD Sharma Class 9 Solutions Chapter 5 Factorisation of Algebraic Expressions Ex 5.4

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 5 Factorisation of Algebraic Expressions Ex 5.4

Other Exercises

Factorize each of the following expressions:
Question 1.
a3 + 8b3 + 64c3 – 24abc
Solution:
We know that
a3 + b3 + c3 – 3abc = (a + b + c) (a2 + b2 + c2 – ab – bc – ca)
a3 + 8b3 + 64c3 – 24abc
= (a)3 + (2b)3 + (4c)3 – 3 x a x 2b x 4c
= (a + 2b + 4c) [(a)2 + (2b)2 + (4c)2 -a x 2b – 2b x 4c – 4c x a]
= (a + 2b + 4c) (a2 + 4b2 + 16c2 – 2ab – 8bc – 4ca)

Question 2.
x3 – 8y3 + 27z3 + 18xyz
Solution:
x3 – 8y3 + 27z3 + 18xyz
= (x)3 + (-2y)3 + (3z)3 – 3 x x x (-2y) (3 z)
= (x – y + 3z) (x2 + 4y2 + 9z2 + 2xy + 6yz – 3zx)

Question 3.
27x3 – y3 – z3 – 9xyz          [NCERT]
Solution:
27x3-y3-z3-9xyz
= (3x)3 + (-y)3 + (-z)3 – 3 x 3x x (-y) (-z)
= (3x – y – z) [(3x)2 + (-y)2 + (-z)2 – 3x x (-y) – (-y) (-z)-  (- z x 3x)]
= (3x-y – z) (9x2 + y2 + z2 + 3xy – yz + 3zx)

Question 4.
RD Sharma Class 9 Solutions Chapter 5 Factorisation of Algebraic Expressions Ex 5.4 Q4.1
Solution:
RD Sharma Class 9 Solutions Chapter 5 Factorisation of Algebraic Expressions Ex 5.4 Q4.2

Question 5.
8x3 + 27y3 – 216z3 + 108xyz
Solution:
8x3 + 27y3 – 216z3 + 108xyz
= (2x)3 + (3y)3 + (6z)3 – 3 x (2x) (3y) (-6z)
= (2x + 3y – 6z) [(2x)2 + (3y)2 + (-6z)2 – 2x x 3y – 3y x (-6z) – (-6z) x 2x]
= (2x + 3y – 6z) (4x2 + 92 + 36z2 – 6xy + 18yz + 12zx)

Question 6.
125 + 8x3 – 27y3 + 90xy
Solution:
125 + 8X3 – 27y3 + 90xy
= (5)3 + (2x)3 + (-3y)3 – [3 x 5 x 2x x (-3y)]
= (5 + 2x – 3y) [(5)2 + (2x)2 + (-3y)2 – 5 x 2x – 2x (-3y) – (-3y) x 5]
= (5 + 2x – 3y) (25 + 4x2 + 9y2– 10x + 6xy + 15y)

Question 7.
8x3 – 125y3 + 180xy + 216
Solution:
8x3 – 125y3 + 180xy + 216
= (2x)3 + (-5y)3 + (6)3 – 3 x 2x (-5y) x 6
= (2x – 5y + 6) [(2x)2 + (-5y)2 + (6)2 – 2x x (-5y) – (-5y) x 6 – 6 x 2x]
= (2x -5y + 6) (4x2 + 25y2 + 36 + 10xy + 30y – 12x)

Question 8.
Multiply:
(i) x2 +y2 + z2 – xy + xz + yz by x + y – z
(ii) x2 + 4y2 + z2 + 2xy + xz – 2yz by x- 2y-z
(iii) x2 + 4y2 + 2xy – 3x + 6y + 9 by x – 2y + 3
(iv) 9x2 + 25y2 + 15xy + 12x – 20y + 16 by 3x  – 5y + 4
Solution:
(i)  (x2 + y2 + z2 – xy + yz + zx) by (x + y – z)
= x3 +y3 – z3 + 3xyz
(ii) (x2 + 4y2 + z2 + 2xy + xz – 2yz) by (x – 2y – z)
= (x -2y-z) [x2 + (-2y)2 + (-z)2 -x x (- 2y) – (-2y) (z) – (-z) (x)]
= x3 + (-2y)3 + (-z)3 – 3x (-2y) (-z)
= x3 – 8y3 – z3 – 6xyz
(iii) x2 + 4y2 + 2xy – 3x + 6y + 9 by x – 2y + 3
= (x – 2y + 3) (x2 + 4y2 + 9 + 2xy + 6y – 3x)
= (x)3 + (-2y)3 + (3)3 – 3 x x x (-2y) x 3 = x3 – 8y3 + 27 + 18xy
(iv) 9x2 + 25y3 + 15xy + 12x – 20y + 16 by 3x – 5y + 4
= (3x -5y + 4) [(3x)2 + (-5y)2 + (4)2 – 3x x (-5y) (-5y x 4) – (4 x 3x)]
= (3x)3 + (-5y)3 + (4)3 – 3 x 3x (-5y) x 4
= 27x3 – 12573 + 64 + 180xy

Question 9.
(3x – 2y)3 + (2y – 4z)3 + (4z – 3x)3
Solution:
(3x – 2y)3 + (2y – 4z)3 +   (4z – 3x)3
 ∵ 3x – 2y + 2y – 4z + 4z – 3x = 0
∴ (3x – 2y)3 + (2y – 4z)3 + (4z – 3x)3
= 3(3x – 2y) (2y – 4z) (4z – 3x)               {∵ x3 + y3 + z3 = 3xyz if x + y + z = 0}

Question 10.
(2x – 3y)3 + (4z – 2x)3  + (3y – 4z)3
Solution:
(2x – 3y)3 + (4z – 2x)3 + (3y – 4z)3
∵  2x – 3y + 4z – 2x + 3y – 4z = 0
∴ (2x – 3y)3 + (4z – 2x)3 + (3y – 4z)3
= (2x – 3y) (4z – 2x) (3y – 4z)                {∵ x3 + y3 + z3 = 3xyz if x + y + z = 0}

Question 11.
RD Sharma Class 9 Solutions Chapter 5 Factorisation of Algebraic Expressions Ex 5.4 Q11.1
Solution:
RD Sharma Class 9 Solutions Chapter 5 Factorisation of Algebraic Expressions Ex 5.4 Q11.2
RD Sharma Class 9 Solutions Chapter 5 Factorisation of Algebraic Expressions Ex 5.4 Q11.3

Question 12.
(a – 3b)3 + (3b – c)3 + (c – a)3
Solution:
(a- 3b)3 + (3b – c)3 + (c – a)3
∵ a – 3b + 3b – c + c – a = 0
∴  (a – 3b)3 + (3b – c)3 + (c – a)3
= 3(a – 3b) (3b – c) (c – a)                       {∵ a3 + b3 + c3 = 3abc if a + b + c = 0}

Question 13.
RD Sharma Class 9 Solutions Chapter 5 Factorisation of Algebraic Expressions Ex 5.4 Q13.1
Solution:
RD Sharma Class 9 Solutions Chapter 5 Factorisation of Algebraic Expressions Ex 5.4 Q13.2

Question 14.
RD Sharma Class 9 Solutions Chapter 5 Factorisation of Algebraic Expressions Ex 5.4 Q14.1
Solution:
RD Sharma Class 9 Solutions Chapter 5 Factorisation of Algebraic Expressions Ex 5.4 Q14.2

Question 15.
2 \(\sqrt { 2 } \) a3+ 16\(\sqrt { 2 } \) b3 + c3 – 12abc
Solution:
RD Sharma Class 9 Solutions Chapter 5 Factorisation of Algebraic Expressions Ex 5.4 Q15.1

Question 16.
Find the value of x3 + y3 – 12xy + 64, when x + y = -4
Solution:
x3 + y3 – 12xy + 64
x + y = -4
Cubing both sides,
x3 + y3 + 3 xy(x + y) = -64
Substitute the value of (x + y)
⇒ x2 + y2 + 3xy x (-4) = -64
⇒  x3 + y2 – 12xy + 64 = 0

Hope given RD Sharma Class 9 Solutions Chapter 5 Factorisation of Algebraic Expressions Ex 5.4 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 9 Solutions Chapter 5 Factorisation of Algebraic Expressions Ex 5.3

by

RD Sharma Class 9 Solutions Chapter 5 Factorisation of Algebraic Expressions Ex 5.3

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 5 Factorisation of Algebraic Expressions Ex 5.3

Other Exercises

Factorize:
Question 1.
64a3 + 125b3 + 240a2b + 300ab2
Solution:
64a3 + 125b3 + 240a2b + 300ab2
= (4a)3 + (5b)3 + 3 x (4a)2 x 5b + 3(4a) + (5b)2
= (4a + 5b)3
= (4a + 5b) (4a + 5b) (4a + 5b)

Question 2.
125x3 – 27y3 – 225x2y + 135xy2
Solution:
125x3 – 27y3 – 225x2y + 135xy2
= (5x)3 – (3y)3 – 3 x (5x)2 x (3y) + 3- x 5x x (3y)2
= (5x – 3y)3
= (5x – 3y) (5x – 3y) (5x – 3y)

Question 3.
RD Sharma Class 9 Solutions Chapter 5 Factorisation of Algebraic Expressions Ex 5.3 Q3.1
Solution:
RD Sharma Class 9 Solutions Chapter 5 Factorisation of Algebraic Expressions Ex 5.3 Q3.2

Question 4.
8x3 + 27y3 + 36x2y + 54xy2
Solution:
8x3 + 27y3 + 16x2y + 54xy2
= (2x)3 + (3y)3 + 3 x (2x)2 x 3y  +  3 x 2x x (3y)2
= (2x + 3y)3
= (2x + 3y) (2x + 3y) (2x + 3y)

Question 5.
a3 – 3a2b + 3ab2 – b3 + 8
Solution:
a3 – 3a2b + 3ab2 – b3 + 8
= (a – b)3 + (2)3
= (a – b + 2) [(a -b)2– (a – b) x 2 + (2)2]
= (a- b + 2) (a2 + b2 -2ab – 2a + 2b + 4)

Question 6.
x3 + 8y3 + 6x2y + 12xy2
Solution:
x3 + 8y3 + 6x2y + 12xy2
= (x)3 + (2y)3 + 3 x x2x 2y + 3 x x x (2y)2
= (x + 2y)3
= (x + 2y) (x + 2y) (x + 2y)

Question 7.
8x3 + y3 + 12x2y + 6xy2
Solution:
8x3 + y3 + 12x2y + 6xy2
= (2x)3 + (y)3 + 3 x (2x)2 x y + 3 x 2x x y2
= (2x + y)3
= (2x + y) (2x + y) (2x + y)

Question 8.
8a3 + 27b3 + 36a2b + 54ab2
Solution:
8a3 + 27b3 + 16a2b + 54ab2
= (2a)3 + (3b)3 + 3 x (2a)2 x 3b + 3 x 2a x (3b)2
= (2a + 3b)3
= (2a + 3b) (2a + 3b) (2a + 3b)

Question 9.
8a3 – 27b3 – 36a2b + 54ab2
Solution:
8a3 – 27b3 – 36a2b + 54ab2
= (2a)3 – (3b)3 – 3 x (2a)2 x 3b + 3 x 2a x (3b)2
= (2a – 3b))3
= (2a – 3b) (2a – 3b) (2a – 3b)

Question 10.
x3 – 12x(x – 4) – 64
Solution:
x3 – 12x(x – 4) – 64
= x3 – 12x2 + 48x – 64
= (x)3 – 3 x x2 x 4 + 3 x x x (4)2– (4)3
= (x – 4)3
= (x – 4) (x – 4) (x – 4)

Question 11.
a3x3 – 3a2bx2 + 3ab2x – b3
Solution:
a3x3 – 3a2bx2 + 3ab2x – b3
= (ax)3 – 3 x (ax)2 x  b + 3 x ax x (b)2– (b)3
= (ax – b)3
= (ax – b) (ax – b) (ax – b)

 

Hope given RD Sharma Class 9 Solutions Chapter 5 Factorisation of Algebraic Expressions Ex 5.3 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 9 Solutions Chapter 5 Factorisation of Algebraic Expressions Ex 5.2

by

RD Sharma Class 9 Solutions Chapter 5 Factorisation of Algebraic Expressions Ex 5.2

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 5 Factorisation of Algebraic Expressions Ex 5.2

Other Exercises

Factorize each of the following expressions:
Question 1.
p3 + 27
Solution:
We know that a3 + b3 = (a + b) (a2 – ab + b2)
a3 – b3 = (a – b) (a2 + aft + b2)
p3 + 21 = (p)3 + (3)3
= (p + 3) (p2– p x 3 + 32)
= (p + 3) (p2 – 3p + 9)

Question 2.
y3 + 125
Solution:
y3 + 125 = (p)3 + (5)3
= (p + 5) (p2 – 5y + 52)
= (P + 5) (p2 – 5y + 25)

Question 3.
1 – 21a3
Solution:
1 – 21a3 = (1)3 – (3a)3
= (1 – 3a) [12 + 1 x 3a + (3a)2]
= (1 – 3a) (1 + 3a + 9a2)

Question 4.
8x3y3 + 27a3
Solution:
8x3y3 + 27a3
= (2xy + 3a) [(2xy)2 – 2xy x 3a + (3a)2]
= (2xy + 3a) (4x2y – 6xya + 9a2)

Question 5.
64a3 – b3
Solution:
64a3 – b3 = (4a)3 – (b)3
= (4a – b) [(4a)2 + 4a x b + (b)2]
= (4a – b) (16a2 + 4ab + b2)

Question 6.
RD Sharma Class 9 Solutions Chapter 5 Factorisation of Algebraic Expressions Ex 5.2 Q6.1
Solution:
RD Sharma Class 9 Solutions Chapter 5 Factorisation of Algebraic Expressions Ex 5.2 Q6.2

Question 7.
10x4– 10xy4
Solution:
I0x4y- 10xy4 = 10xy(x3 -y3)
= 10xy(x – y) (x2 + xy + y2)

Question 8.
54x6y + 2x3y4
Solution:
54 x6y + 2x3y4 = 2x3y(27x3 + y3)
= 2x3y[(3x)3 + (y)3]
= 2x3y(3x + y) [(3x)2 -3x x y + y2]
= 2x3y(3x + y) (9x2 -3xy + y2)

Question 9.
32a3 + 108b3
Solution:
32a3 + 108b3
= 4(8a3 + 27b3) = 4 [(2a)3 + (3 b)3]
= 4(2a + 3b) [(2a)2 – 2a x 3b + (3b)2]
= 4(2a + 3b) (4a2 – 6ab + 9b2)

Question 10.
(a – 2b)3 – 512b3
Solution:
(a – 2b)3 – 512b3
= (a – 2b)3 – (8b)3
= (a – 2b- 8b) [(a – 2b)2 + (a – 2b) x 8b + (8b)2]
= (a – 10b) [a2 + 4b2 – 4ab + 8ab – 16b2 + 64b2]
= (a – 10b) (a2 + 4ab + 52b2)

Question 11.
8x2y3 – x5
Solution:
8x2y3 – x5 = x2(8y3 – X3)
= x2(2y)3 – (x)3]
= x2[(2y – x) (2y)2 + 2y x x + (x)2]
= x2(2y – x) (4y2 + 2xy + x2)

Question 12.
1029 -3x3
Solution:
1029 – 3X3 = 3(343 – x3)                       ‘
= 3 [(7)3 – (x)3]
= 3(7 – x) (49x + 7x + x2)

Question 13.
x3y3+ 1
Solution:
x3y3 + 1 = (xy)3 + (1)3
= (xy + 1) [(xy)2 – xy x 1 + (1)2]
= (xy + 1) (x2y2 – xy + 1)
= (xy + 1) (x2y – xy + 1)

Question 14.
x4y4 – xy
Solution:
x4y4 – xy = xy(x3y3 – 1)
= xy[(xy3-(1)3]
= xy (xy – 1) [x2y2 + 2xy + 1]

Question 15.
a3 + b3 + a + b
Solution:
a3 + b3 + a + b
= (a + b) (a2 – ab + b2) + 1 (a + b)
= (a + b) (a2 – ab + b2 + 1)

Question 16.
Simplify:
RD Sharma Class 9 Solutions Chapter 5 Factorisation of Algebraic Expressions Ex 5.2 Q16.1
Solution:
RD Sharma Class 9 Solutions Chapter 5 Factorisation of Algebraic Expressions Ex 5.2 Q16.2
RD Sharma Class 9 Solutions Chapter 5 Factorisation of Algebraic Expressions Ex 5.2 Q16.3

Question 17.
(a + b)3 – 8(a – b)3
Solution:
(a + b)3 – 8(a – b)3
= (a + b)2 – (2a – 2b)3
= (a+ b – 2a + 2b) [(a + b)2 + (a + b) (2a-2b) + (2a – 2b)2)]
= (3b – a) [a2 + b2 + 2ab + 2a2 – 2ab + 2ab – 2b2 + 4a2 – 8ab + 4b2]
= (3b – a) [7a2 – 6ab + 3b2]

Question 18.
(x + 2)3 + (x- 2)3
Solution:
(x + 2)3 + (x – 2)3
= (x + 2 + x – 2) [(x + 2)2 – (x + 2) (x – 2) + (x – 2)2]
= 2x [x2 + 4x + 4 – (x2 + 2x – 2x – 4) + x2 4x + 4]
= 2x[x2 + 4x + 4- x2-2x + 2x + 4+ x2– 4x + 4]
= 2x[x2 + 12]

Question 19.
x6 +y6
Solution:
x6 + y6 = (x2)3 + (y2)3
= (x2 + y2) [x4 – x2y2 + y4]

Question 20.
a12 + b12
Solution:
a12 + b12 = (a4)3 + (b4)3
= (a4 + b4) [(a4)2 – a4b4 + (b4)2]
= (a4 + b4) (a8 – a4b4 + b8)

Question 21.
x3 + 6x2 + 12x + 16
Solution:
x3 + 6x2 + 12x + 16
= (x)3 + 3.x2.2 + 3.x.4 + (2)3 + 8           {∵ a3 + 3a2b + 3ab2 +b3 = (a + b)3}
= (x + 2)3 + 8 = (x + 2)3 + (2)3
= (x + 2 + 2) [(x + 2)2 – (x + 2) x 2 + (2)2] {∵ a3 + b2 = (a + b) (a2 – ab + b2}
= (x + 4) (x2 + 4x + 4 – 2x – 4 + 4)
= (x + 4) (x2 + 2x + 4)

Question 22.
RD Sharma Class 9 Solutions Chapter 5 Factorisation of Algebraic Expressions Ex 5.2 Q22.1
Solution:
RD Sharma Class 9 Solutions Chapter 5 Factorisation of Algebraic Expressions Ex 5.2 Q22.2

Question 23.
a3 + 3a2b + 3ab2 + b3 – 8
Solution:
a3 + 3a2b + 3ab2 + b3 – 8
= (a + b)3 – (2)3
= (a + b -2)[(a + b)2 + (a +b)x2 + (2)2]
= (a + b-2) (a2 + b2 + 2ab + 2a + 2b + 4)
= (a + b – 2) (a2 + b2 + 2ab + 2(a + b) + 4]
= (a + b – 2) [(a + b)2 + 2(a + b) + 4}

Question 24.
8a3 – b3 – 4ax + 2bx
Solution:
8a3 – b3 – 4ax + 2bx
(2a)3 – (b)3 – 2x(2a – b)
= (2a-b)[(2a)2 + 2a x b + (b)2]- 2x(2a-b)
= (2a – b) [4a2 + 2ab + b2] – 2x(2a – b)
= (2a – b) [4a2 + 2ab + b2 – 2x]

Hope given RD Sharma Class 9 Solutions Chapter 5 Factorisation of Algebraic Expressions Ex 5.2 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 9 Solutions Chapter 5 Factorisation of Algebraic Expressions Ex 5.1

by

RD Sharma Class 9 Solutions Chapter 5 Factorisation of Algebraic Expressions Ex 5.1

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 5 Factorisation of Algebraic Expressions Ex 5.1

Other Exercises

Factorize
Question 1.
x3 + x – 3x2 – 3
Solution:
x3 + x – 3x2 – 3
x3 – 3a2 + x – 3
⇒  x2(x – 3) + 1(x – 3)
= (x – 3) (x2 + 1)

Question 2.
a(a + b)3 – 3a2b(a + b)
Solution:
a(a + b)3 – 3a2b(a + b)
= a(a + b) {(a + b)2 – 3ab}
= a(a + b) {a2 + b2 + 2ab – 3ab}
= a{a + b) {a2 – ab + b2)

Question 3.
x(x3 – y3) + 3xy(x – y)
Solution:
x(x3 – y3) + 3xy(x – y)
= x(x – y) (x2 + xy + y2) + 3xy(x – y)
= x(x – y) (x2 + xy + y2 + 3y)
= x(x – y) (x2 + xy + y2 + 3y)

Question 4.
a2x2 + (ax2 +1)x + a
Solution:
a2x2 + (ax2 + 1)x + a
= a2x2 + a + (ax2 + 1)x
= a(ax2 + 1) + x(ax2 + 1)
= (ax2 + 1) (a + x)
= (x + a) (ax2 + 1)

Question 5.
x2 + y – xy – x
Solution:
x2 + y – xy – x
= x2-x-xy + y = x(x- l)-y(*- 1)
= (x – 1) (x – y)

Question 6.
X3 – 2x2y + 3xy2 – 6y3
Solution:
x3 – 2x2y + 3xy2 – 6y3
= x2(x – 2y) + 3y2(x – 2y)
= (x – 2y) (x2 + 3y2)

Question 7.
6ab – b2 + 12ac – 2bc
Solution:
6ab – b2 + 12ac – 2bc
= 6ab + 12ac – b2 – 2bc
= 6a(b + 2c) – b(b + 2c)
= (b + 2c) (6a – b)

Question 8.
x(x – 2) (x – 4) + 4x – 8
Solution:
x(x – 2) (x – 4) + 4x – 8
= x(x – 2) (x – 4) + 4(x – 2)
= (x – 2) [x(x – 4) + 4]
= (x – 2) (x2 – 4x + 4)
= (x – 2) [(x)2 – 2 x x x 2 + (2)2]
= (x – 2) (x – 2)2 = (x – 2)3

Question 9.
(a – b + c)2 + (b – c + a)2 + 2(a – b + c) (b – c + a)
Solution:
(a – b + c)2 + ( b- c+a)2 + 2(a – b + c) (b – c + a)      {∵ a2 + b2 + 2ab = (a + b)2}
= [a – b + c + b- c + a]2
= (2a)2 = 4a2

Question 10.
a2 + 2ab + b2 – c2
Solution:
a2 + 2ab + b2 – c2
= (a2 + 2ab + b2) – c2
= (a + b)2 – (c)2         {∵  a2 – b2 = (a + b) (a – b)}
= (a + b + c) (a + b – c)

Question 11.
a2 + 4b2 – 4ab – 4c2
Solution:
RD Sharma Class 9 Solutions Chapter 5 Factorisation of Algebraic Expressions Ex 5.1 Q11.1

Question 12.
x2 – y2 – 4xz + 4z2
Solution:
x2 – y2 – 4xz + 4z2
= x2 – 4xz + 4z2 – y2
= (x)2 – 2 x x x 2z + (2z)2 – (y)2
= (x – 2z)2 – (y)2
= (x – 2z + y) (x – 2z – y)
= (x +y – 2z) (x – y – 2z)

Question 13.
RD Sharma Class 9 Solutions Chapter 5 Factorisation of Algebraic Expressions Ex 5.1 Q13.1
Solution:
RD Sharma Class 9 Solutions Chapter 5 Factorisation of Algebraic Expressions Ex 5.1 Q13.2
RD Sharma Class 9 Solutions Chapter 5 Factorisation of Algebraic Expressions Ex 5.1 Q13.3

Question 14.
RD Sharma Class 9 Solutions Chapter 5 Factorisation of Algebraic Expressions Ex 5.1 Q14.1
Solution:
RD Sharma Class 9 Solutions Chapter 5 Factorisation of Algebraic Expressions Ex 5.1 Q14.2

Question 15.
RD Sharma Class 9 Solutions Chapter 5 Factorisation of Algebraic Expressions Ex 5.1 Q15.1
Solution:
RD Sharma Class 9 Solutions Chapter 5 Factorisation of Algebraic Expressions Ex 5.1 Q15.2

Question 16.
Give possible expression for the length and breadth of the rectangle having 35y2 + 13y – 12 as its area.
Solution:
Area of a rectangle = 35y2 + 13y – 12
= 35y2 + 28y- 15y- 12
RD Sharma Class 9 Solutions Chapter 5 Factorisation of Algebraic Expressions Ex 5.1 Q16.1
(i) If length = 5y + 4, then breadth = 7y – 3
(ii) and if length = 7y-3, then length = 5y+ 4

Question 17.
What are the possible expressions for the dimensions of the cuboid whose volume is 3x2 – 12x.
Solution:
Volume 3x2 – 12x
= 3x(x – 4)
∴ Factors are 3, x, and x – 4
Now, if length = 3, breadth = x and height = x – 4
if length =3, breadth = x – 4, height = x
if length = x, breadth = 3, height = x – 4
if length = x, breadth = x – 4, height = 3
if length = x – 4, breadth = 3, height = x
if length – x – 4, breadth = x, height = 3

Question 18.
RD Sharma Class 9 Solutions Chapter 5 Factorisation of Algebraic Expressions Ex 5.1 Q18.1
Solution:
RD Sharma Class 9 Solutions Chapter 5 Factorisation of Algebraic Expressions Ex 5.1 Q18.2

Question 19.
(x + 2) (x2 + 25) – 10x2 – 20x
Solution:
(x + 2) (x2 + 25) – 10x2 – 20x
= (x + 2) (x2 + 25) – 10x(x + 2)
= (x + 2) [x2 + 25 – 10x]
= (x + 2) [(x)2 – 2 x x x 5 + (5)2]
= (x + 2) (x – 5)2

Question 20.
2a2 + 2\(\sqrt { 6 } \) ab +3b2
Solution:
2a2 + 2\(\sqrt { 6 } \)  ab +3 b2
= (\(\sqrt { 2 } \) a)2+ \(\sqrt { 2 } \) a x \(\sqrt { 3 } \) b+ (\(\sqrt { 3 } \) b)2
= (\(\sqrt { 2 } \)a + \(\sqrt { 3 } \) b)2

Question 21.
a2 + b2 + 2(ab + bc + ca)
Solution:
a2 + b2 + 2(ab + bc + ca)
= a2 + b2 + 2 ab + 2 bc + 2 ca
= (a + b)2 + 2c(b + a)
= (a + b)2 + 2c(a + b)
= (a + b) (a + b + 2c)

Question 22.
4(x – y)2 – 12(x -y) (x + y) + 9(x + y)2
Solution:
4(x – y)2 – 12(x – y) (x + y) + 9(x + y)2
= [2(x – y)2 + 2 x 2(x – y) x 3(x + y) + [3 (x+y]2        {∵ a2 + b2 + 2 abc = (a + b)2}
= [2(x – y) + 3(x + y)]2
= (2x-2y + 3x + 3y)2
= (5x + y)2

Question 23.
a2 – b2 + 2bc – c2
Solution:
a2 – b2 + 2bc – c2
= a2 – (b2 – 2bc + c2)                                           {∵ a2 + b2 – 2abc = (a – b)2}
= a2 – (b – c)2
= (a)2 – (b – c)2          {∵ a2 – b2 = (a + b) (a – b)}
= (a + b – c) (a – b + c)

Question 24.
xy9 – yx9
Solution:
xy9 – yx9 = xy(y8 – x8)
= -xy(x8 – y8)
= -xy[(x4)2 – (y4)2]
= -xy (x4 + y4) (x4 – y4)                                         {∵ a2-b2 = (a + b) (a – b)}
= -xy (x4 + y4) {(x2)2 – (y2)2}
= -xy(x4 + y4) (x2 + y2) (x2 – y2)
= -xy (x4 +y4) (x2 + y2) (x + y) (x -y)
= -xy(x – y) (x + y) (x2 + y2) (x4 + y4)

Question 25.
x4 + x2y2 + y4
Solution:
x4 + x2y2 + y4  = (x2)2 + 2x2y2 + y4 – x2y2           (Adding and subtracting x2y2)
= (x2 + y2)2 – (xy)2                                                        {∵ a2 – b2 = (a + b) (a – b)}
= (x2 + y2 + xy) (x2 + y2 – xy)
= (x2 + xy + y2) (x2 – xy + y2)

Question 26.
x2 + 6\(\sqrt { 2 } \)x + 10
Solution:
RD Sharma Class 9 Solutions Chapter 5 Factorisation of Algebraic Expressions Ex 5.1 Q26.1

Question 27.
x2 + 2\(\sqrt { 2 } \)x- 30
Solution:
RD Sharma Class 9 Solutions Chapter 5 Factorisation of Algebraic Expressions Ex 5.1 Q27.1

Question 28.
x2 – \(\sqrt { 3 } \)x – 6
Solution:
RD Sharma Class 9 Solutions Chapter 5 Factorisation of Algebraic Expressions Ex 5.1 Q28.1

Question 29.
x2 + 5 \(\sqrt { 5 } \)x + 30
Solution:
RD Sharma Class 9 Solutions Chapter 5 Factorisation of Algebraic Expressions Ex 5.1 Q29.1

Question 30.
x2 + 2 \(\sqrt { 3 } \)x – 24
Solution:
RD Sharma Class 9 Solutions Chapter 5 Factorisation of Algebraic Expressions Ex 5.1 Q30.1

Question 31.
5 \(\sqrt { 5 } \)x2 + 20x + 3\(\sqrt { 5 } \)
Solution:
RD Sharma Class 9 Solutions Chapter 5 Factorisation of Algebraic Expressions Ex 5.1 Q31.1

Question 32.
2x2 + 3\(\sqrt { 5 } \) x + 5
Solution:
RD Sharma Class 9 Solutions Chapter 5 Factorisation of Algebraic Expressions Ex 5.1 Q32.1

Question 33.
9(2a – b)2 – 4(2a – b) – 13
Solution:
RD Sharma Class 9 Solutions Chapter 5 Factorisation of Algebraic Expressions Ex 5.1 Q33.1

Question 34.
7(x-2y) – 25(x-2y) +12
Solution:
RD Sharma Class 9 Solutions Chapter 5 Factorisation of Algebraic Expressions Ex 5.1 Q34.1

Question 35.
2(x+y) – 9(x+y) -5
Solution:
2(x+y) – 9(x+y) -5
RD Sharma Class 9 Solutions Chapter 5 Factorisation of Algebraic Expressions Ex 5.1 Q35.1

Hope given RD Sharma Class 9 Solutions Chapter 5 Factorisation of Algebraic Expressions Ex 5.1 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.