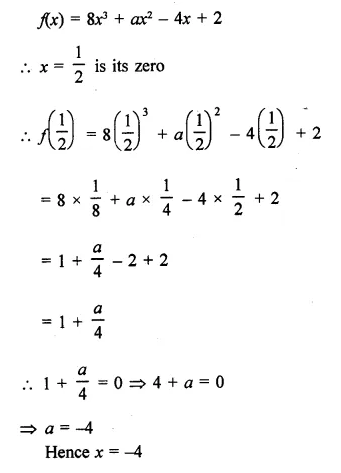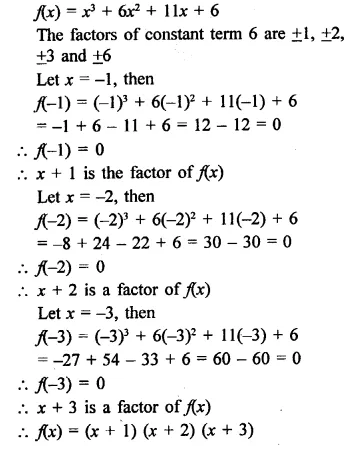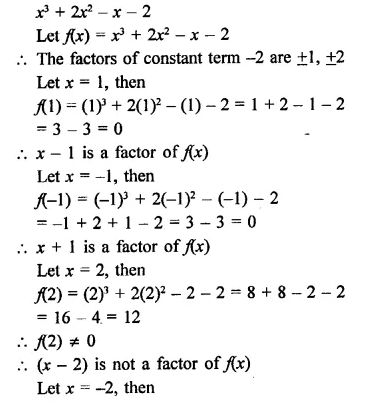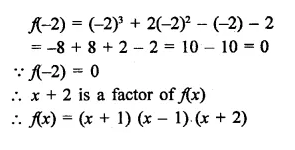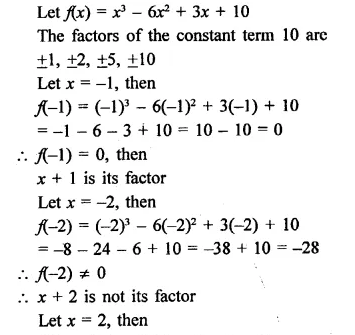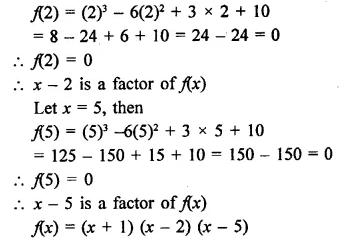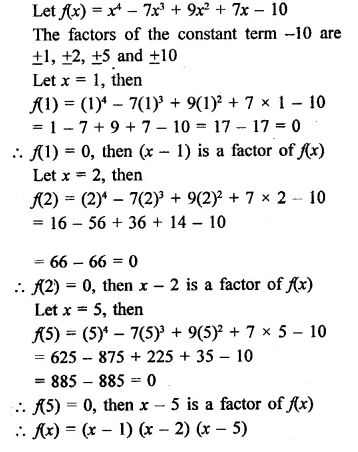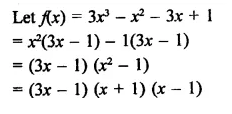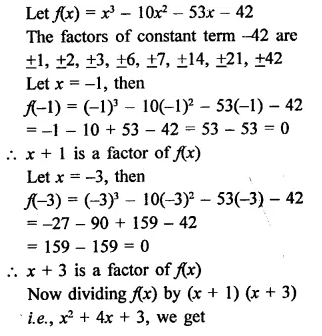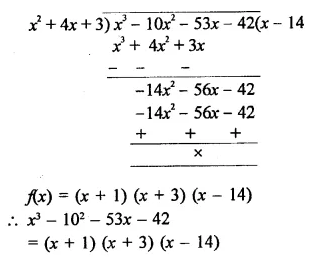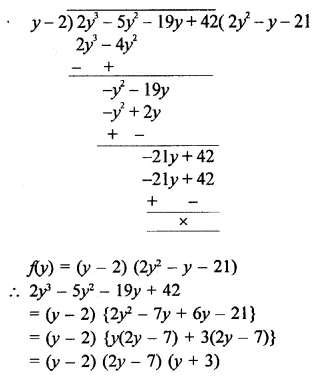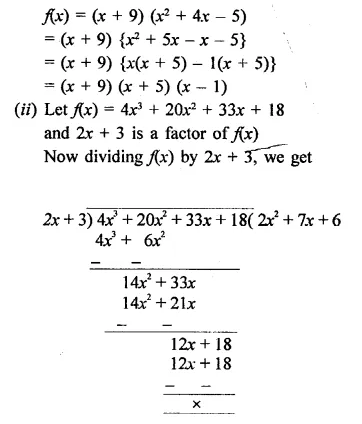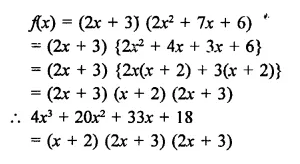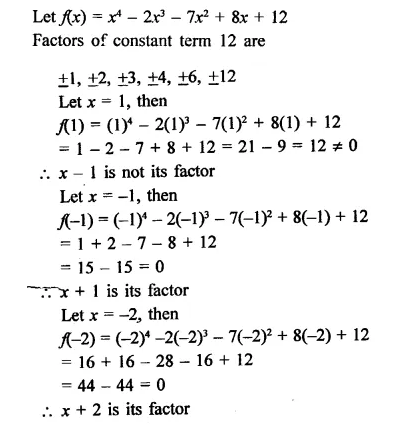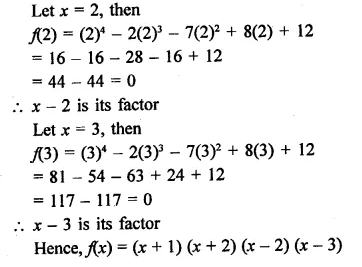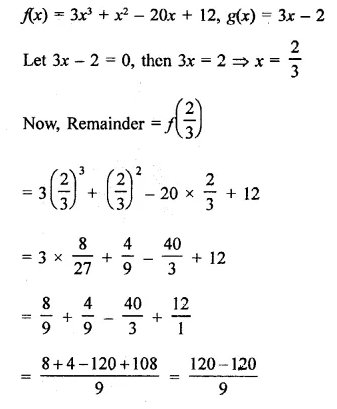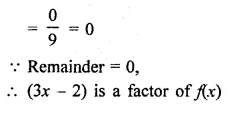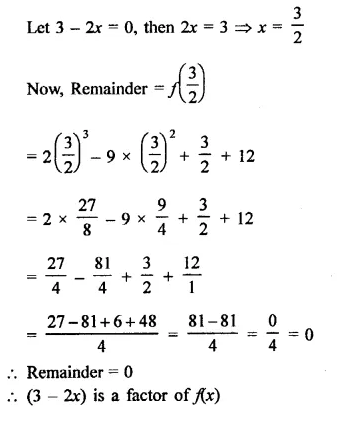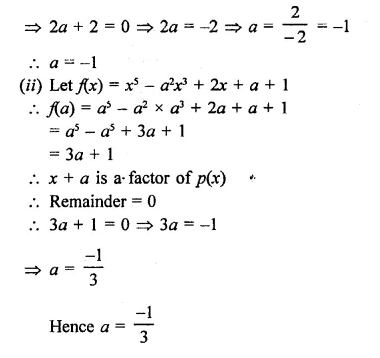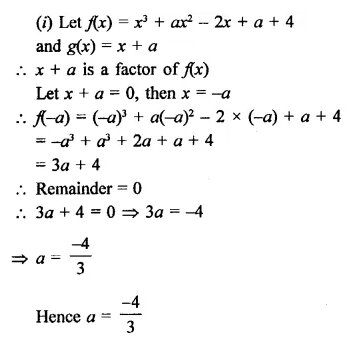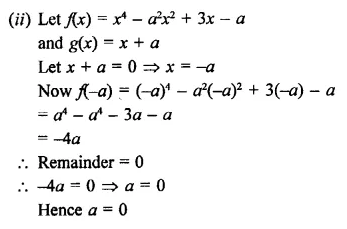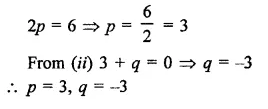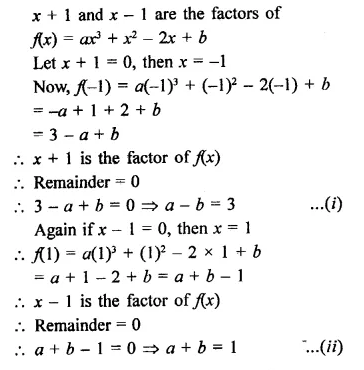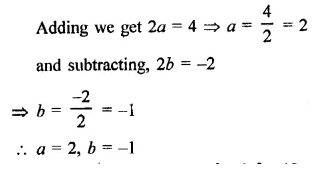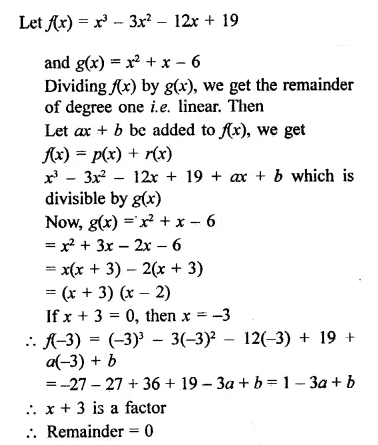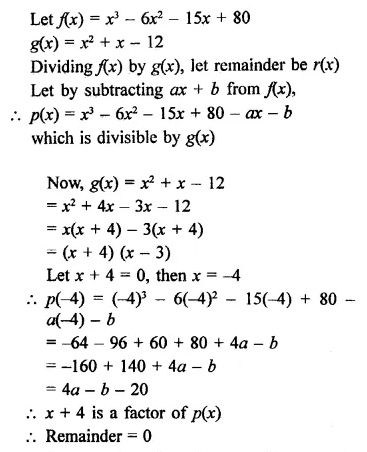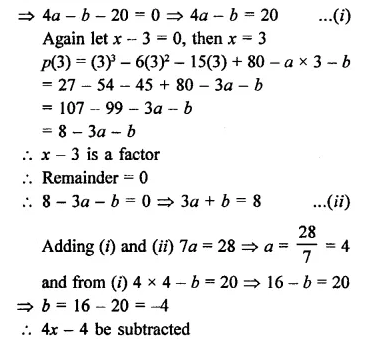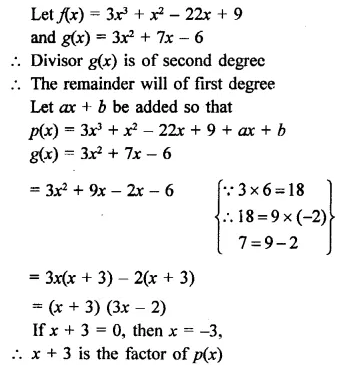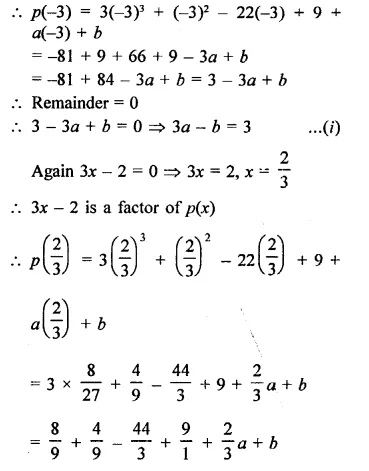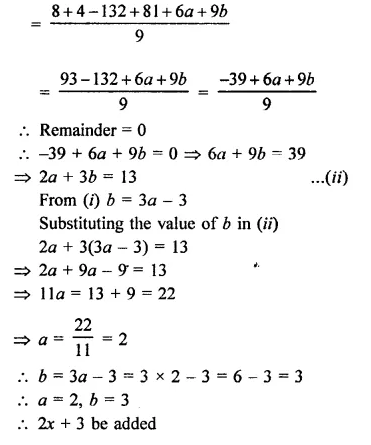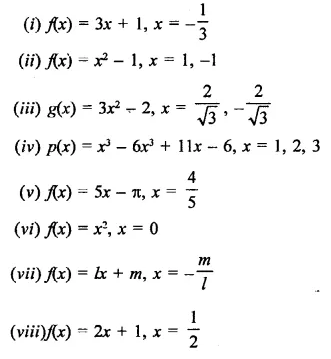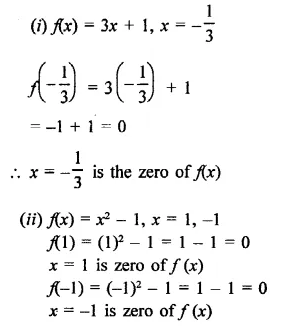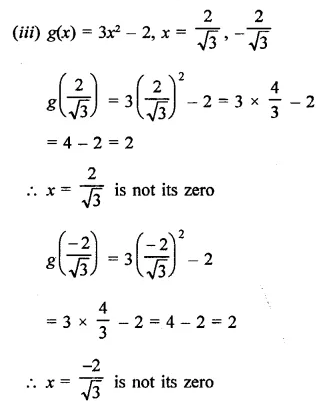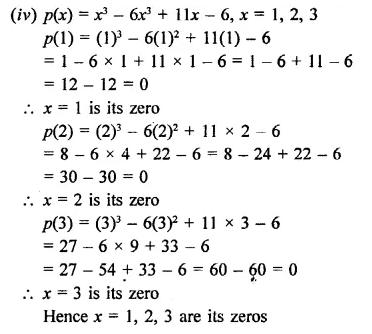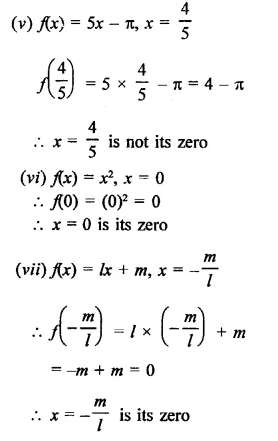Maths Class 9 RD Sharma Solutions

RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials VSAQS

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials VSAQS

Other Exercises

• RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials Ex 6.1
• RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials Ex 6.2
• RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials Ex 6.3
• RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials Ex 6.4
• RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials Ex 6.5
• RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials VSAQS
• RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials MCQS

Question 1.
Define zero or root of a polynomial.
Solution:
A real number a is a zero or root of a polynomial f(x) if f(α) = 0

Question 2.
If x = \(\frac { 1 }{ 2 }\) is a zero of the polynomial f(x) =  8x³ + ax² – 4x + 2, find the value of a.
Solution:

Question 3.
Write the remainder when the polynomial f(x) = x³+x²-3x + 2is divided by x + 1.
Solution:
f(x) = x³+x²-3x + 2
Let x + 1 = 0, then x = -1
∴ Remainder =(-1)
Now,f(-1) = (-1)³ + (-1)² – 3(-1) + 2
= -1 + 1+ 3 + 2 = 5
∴ Remainder = 5

Question 4.
Find the remainder when x³ + 4x² + 4x – 3 is divided by x.
Solution:
f(x) = x³ + 4x² + 4x – 3
Dividing f(x) by x, we get
Let x = 0, then
f(x) = 0 + 0 + 0 – 3 = -3
∴  Remainder = -3

Question 5.
If x + 1 is a factor of x³ + a, then write the value of a.
Solution:
Let f(x) = x³ + a
∴ x + 1 is a factor of fx)
Let x + 1 = 0
⇒ x = -1
∴ f(-1) = x³ + a
= (-1)³ + a = -1 + a
∴  x + 1 is a factor
∴  Remainder = 0
∴  -1 + a = 0 ⇒  a = 1
Hence a = 1

Question 6.
If f(x) = x⁴-2x³ + 3x² – ax – b when divided by x – 1, the remainder is 6, then find the value of a + b.
Solution:
f(x) = x⁴ – 2x³ + 3x² – ax – b
Dividing f(x) by x – 1, the remainder = 6
Now let x – 1 = 0, then x = 1
∴  f(1) = (1)⁴ – 2(1)³ + 3(1)² -ax 1-b
= 1 -2 + 3-a-b = 2-a-b
∴ Remainder = 6
∴ 2 – a – b = 6  ⇒ a + b = 2 – 6 = -4
Hence a + b = -4

Hope given RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials VSAQS are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials Ex 6.5

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials Ex 6.5

Other Exercises

• RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials Ex 6.1
• RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials Ex 6.2
• RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials Ex 6.3
• RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials Ex 6.4
• RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials Ex 6.5
• RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials VSAQS
• RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials MCQS

Using factor theorem, factorize each of the following polynomials:
Question 1.
x³ + 6x² + 11x + 6
Solution:

Question 2.
x³ + 2x² – x – 2
Solution:

Question 3.
x³ – 6x² + 3x + 10
Solution:

Question 4.
x⁴ – 7x³ + 9x² + x- 10
Solution:

Question 5.
3x³ – x² – 3x + 1
Solution:

Question 6.
x³ – 23x² + 142x – 120        [NCERT]
Solution:

Question 7.
y³ – 7y + 6
Solution:
Let f(y) = y³ – 7y + 6

Question 8.
X³ -10x² – 53x – 42
Solution:

Question 9.
y³ – 2y²– 29y – 42
Solution:

Question 10.
2y³ – 5y² – 19y + 42
Solution:

Question 11.
x³ + 13² + 32x + 20      [NCERT]
Solution:

Question 12.
x³ – 3x² – 9x – 5 [NCERT]
Solution:

Question 13.
2y³+ y² – 2y – 1      [NCERT]
Solution:

Question 14.
x³ – 2x² – x + 2
Solution:

Question 15.
Factorize each of the following polynomials:
(i) x³ + 13x² + 31x – 45 given that x + 9 is a factor
(ii) 4x³ + 20x² + 33x + 18 given that 2x + 3 is a factor
Solution:

Question 16.
x⁴ – 2x³ – 7x² + 8x + 12
Solution:

Question 17.
x⁴ + 10x³ + 35x² + 50x + 24
Solution:

Question 18.
2x⁴ – 7x³ – 13x² + 63x – 45
Solution:

Hope given RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials Ex 6.5 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials Ex 6.4

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials Ex 6.4

Other Exercises

• RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials Ex 6.1
• RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials Ex 6.2
• RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials Ex 6.3
• RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials Ex 6.4
• RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials Ex 6.5
• RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials VSAQS
• RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials MCQS

In each of the following, use factor Theorem to find whether polynomial g(x) is a factor of polynomial f(x) or, not: (1-7)
Question 1.
f(x) = x³ – 6x² + 11x – 6; g(x) = x – 3
Solution:
We know that if g(x) is a factor of p(x),
then the remainder will be zero. Now,
f(x) = x³ – 6x² + 11x – 6; g(x) = x -3
Let x – 3 = 0, then x = 3
∴ Remainder = f(3)
= (3)³ – 6(3)² +11 x 3 – 6
= 27-54 + 33 -6
= 60 – 60 – 0
∵  Remainder is zero,
∴ x – 3 is a factor of f(x)

Question 2.
f(x) = 3X⁴ + 17x³ + 9x² – 7x – 10; g(x) = x + 5
Solution:
f(x) = 3x⁴ + 17X³ + 9x² – 7x – 10; g(x) = x + 5
Let x + 5 = 0, then x = -5
∴  Remainder = f(-5) = 3(-5)⁴ + 17(-5)³ + 9(-5)² – 7(-5) – 10
= 3 x 625 + 17 x (-125) + 9 x (25) – 7 x (-5) – 10
= 1875 -2125 + 225 + 35 – 10
= 2135 – 2135 = 0
∵  Remainder = 0
∴ (x + 5) is a factor of f(x)

Question 3.
f(x) = x⁵ + 3x⁴ – x³ – 3x² + 5x + 15, g(x) = x + 3
Solution:
f(x) = x⁵ + 3X⁴ – x³ – 3x² + 5x + 15, g(x) = x + 3
Let x + 3 = 0, then x = -3
∴ Remainder = f(-3)
= (-3)⁵ + 3(-3)⁴ – (-3)³ – 3(-3)² + 5(-3) + 15
= -243 + 3 x 81 -(-27)-3 x 9 + 5(-3) + 15
= -243 +243 + 27-27- 15 + 15
= 285 – 285 = 0
∵  Remainder = 0
∴  (x + 3) is a factor of f(x)

Question 4.
f(x) = x³ – 6x² – 19x + 84, g(x) = x – 7
Solution:
f(x) = x³ – 6x² – 19x + 84, g(x) = x – 7
Let x – 7 = 0, then x = 7
∴  Remainder = f(7)
= (7)³ – 6(7)² – 19 x 7 + 84
= 343 – 294 – 133 + 84
= 343 + 84 – 294 – 133
= 427 – 427 = 0
∴  Remainder = 0
∴ (x – 7) is a factor of f(x)

Question 5.
f(x) = 3x³  + x² – 20x + 12, g(x) = 3x – 2
Solution:

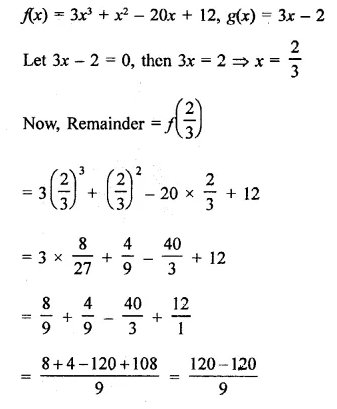
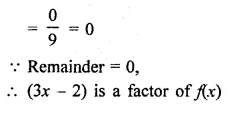
Question 6.
f(x) = 2x³ – 9x² + x + 12, g(x) = 3 – 2x
Solution:
f(x) = 2x³ – 9x² + x + 12, g(x) = 3 – 2x

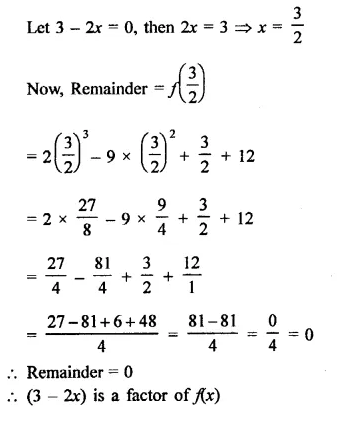
Question 7.
f(x) = x³ – 6x² + 11x – 6, g(x) = x² – 3x + 2
Solution:
g(x) = x² – 3x + 2
= x² – x – 2x + 2
= x(x – 1) – 2(x – 1)
= (x – 1) (x – 2)
If x – 1 = 0, then x = 1
‍∴ f(1) = (1)³ – 6(1)² + 11(1) – 6
= 1-6+11-6= 12- 12 = 0
‍∴ Remainder is zero
‍∴ x – 1 is a factor of f(x)
and if x – 2 = 0, then x = 2
∴ f(2) = (2)³ – 6(2)² + 11(2)-6
= 8 – 24 + 22 – 6 = 30 – 30 = 0
‍∴ Remainder = 0
‍∴ x – 2 is also a factor of f(x)

Question 8.
Show that (x – 2), (x + 3) and (x – 4) are factors of x³ – 3x² – 10x + 24.
Solution:
f(x) = x³ – 3x² – 10x + 24
Let x – 2 = 0, then x = 2
Now f(2) = (2)³ – 3(2)² – 10 x 2 + 24
= 8 – 12 – 20 + 24 = 32 – 32 = 0
‍∴ Remainder = 0
‍∴ (x – 2) is the factor of f(x)
If x + 3 = 0, then x = -3
Now, f(-3) = (-3)³ – 3(-3)² – 10 (-3) + 24
= -27 -27 + 30 + 24
= -54 + 54 = 0
∴ Remainder = 0
∴ (x + 3) is a factor of f(x)
If x – 4 = 0, then x = 4
Now f(4) = (4)³ – 3(4)² – 10 x 4 + 24 = 64-48 -40 + 24
= 88 – 88 = 0
∴ Remainder = 0
∴ (x – 4) is a factor of (x)
Hence (x – 2), (x + 3) and (x – 4) are the factors of f(x)

Question 9.
Show that (x + 4), (x – 3) and (x – 7) are factors of x³ – 6x² – 19x + 84.
Solution:
Let f(x) = x³ – 6x² – 19x + 84
If x + 4 = 0, then x = -4
Now, f(-4) = (-4)³ – 6(-4)² – 19(-4) + 84
= -64 – 96 + 76 + 84
= 160 – 160 = 0
∴ Remainder = 0
∴ (x + 4) is a factor of f(x)
If x – 3 = 0, then x = 3
Now, f(3) = (3)³ – 6(3)² – 19 x 3 + 84
= 27 – 54 – 57 + 84
= 111 -111=0
∴ Remainder = 0
∴ (x – 3) is a factor of f(x)
and if x – 7 = 0, then x = 7
Now, f(7) = (7)³ – 6(7)² – 19 x 7 + 84
= 343 – 294 – 133 + 84
= 427 – 427 = 0
∴ Remainder = 0
∴ (x – 7) is also a factor of f(x)
Hence (x + 4), (x – 3), (x – 7) are the factors of f(x)

Question 10.
For what value of a (x – 5) is a factor of x³ – 3x² + ax – 10?
Solution:
f(x) = x³ – 3x² + ax – 10
Let x – 5 = 0, then x = 5
Now, f(5) = (5)³ – 3(5)² + a x 5 – 10
= 125 – 75 + 5a – 10
= 125 – 85 + 5a = 40 + 5a
∴ (x – 5) is a factor of fix)
∴ Remainder = 0
⇒  40 + 5a = 0 ⇒  5a = -40
⇒ a = \(\frac { -40 }{ 5 }\)= -8
Hence a = -8

Question 11.
Find the value of a such that (x – 4) is a factor of 5x³ – 7x² – ax – 28.
Solution:
Let f(x) =  5x³ – 7x² – ax – 28
and Let x – 4 = 0, then x = 4
Now, f(4) = 5(4)³ – 7(4)² – a x 4 – 28
= 5 x 64 – 7 x 16 – 4a – 28
= 320 – 112 – 4a – 28
= 320 – 140 – 4a
= 180 – 4a
∴ (x – 4) is a factor of f(x)
∴ Remainder = 0
⇒  180 -4a = 0
⇒  4a = 180
⇒  a = \(\frac { 180 }{ 4 }\) =  45
∴  a = 45

Question 12.
Find the value of a, if x + 2 is a factor of 4x⁴ + 2x³ – 3x² + 8x + 5a.
Solution:
Let f(x) = 4x⁴ + 2x³ – 3x² + 8x + 5a
and Let x + 2 = 0, then x = -2
Now, f(-2) = 4(-2)⁴ + 2(-2)³ – 3(-2)² + 8 x ( 2) + 5a
= 4 x 16 + 2(-8) – 3(4) + 8 (-2) + 5a
= 64- 16- 12- 16 +5a
= 64 – 44 + 5a
= 20 + 5a
∴  (x + 2) is a factor of fix)
∴  Remainder = 0
⇒  20 + 5a = 0 ⇒  5a = -20
⇒  a =\(\frac { -20 }{ 5 }\)  = -4
∴ a = -4

Question 13.
Find the value of k if x – 3 is a factor of k²x³ – kx² + 3kx – k.
Solution:
Let f(x) = k²x³ – kx² + 3kx – k
and Let x – 3 = 0, then x = 3
Now,f(3) = k²(3)³ – k(3)² + 3k(3) – k
= 27k² – 9k + 9k-k
= 27k²-k
∴ x – 3 is a factor of fix)
∴ Remainder = 0
∴ 27k² – k = 0
⇒ k(27k – 1) = 0 Either k = 0
or 21k – 1 = 0
⇒ 21k = 1
∴  k= \(\frac { 1 }{ 27 }\)
∴  k = 0,\(\frac { 1 }{ 27 }\)

Question 14.
Find the values of a and b, if x² – 4 is a factor of ax⁴ + 2x³ – 3x² + bx – 4.
Solution:
f(x) = ax⁴ + 2x³ – 3x² + bx – 4
Factors of x² – 4 = (x)² – (2)²
= (x + 2) (x – 2)
If x + 2 = 0, then x = -2
Now, f(-2) = a(-2)⁴ + 2(-2)³ – 3(-2)² + b(-2) – 4
16a- 16 – 12-26-4
= 16a -2b-32
∵ x + 2 is a factor of f(x)
∴ Remainder = 0
⇒  16a – 2b – 32 = 0
⇒ 8a – b – 16 = 0
⇒ 8a – b = 16         …(i)
Again x – 2 = 0, then x = 2
Now f(2) = a x (2)⁴ + 2(2)³ – 3(2)² + b x 2-4
= 16a + 16- 12 + 26-4
= 16a + 2b
∵  x – 2 is a factor of f(x)
∴ Remainder = 0
⇒  16a + 2b = 0
⇒ 8a + b= 0                             …(ii)
Adding (i) and (ii),
⇒ 16a = 16
⇒ a = \(\frac { 16 }{ 16 }\) = 1
From (ii) 8 x 1 + b = 0
⇒ 8 + b = 0
⇒  b = – 8
∴ a = 1, b = -8

Question 15.
Find α and β, if x + 1 and x + 2 are factors of x³ + 3x² – 2αx +β.
Solution:
Let f(x) = x³ + 3x² – 2αx + β
and Let x + 1 = 0 then x = -1
Now,f(-1) = (1)³ + 3(-1)² – 2α (-1) +β
= -1 + 3 + 2α + β
= 2 + 2α + β
∵  x + 1 is a factor of f(x)
∴  Remainder = 0
∴ 2 + 2α + β = 0
⇒  2α + β = -2                    …(i)
Again, let x + 2 = 0, then x = -2
Now, f(-2) = (-2)³ + 3(-2)² – 2α(-2) + β
= -8 + 12 + 4α+ β
= 4 + 4α+ β
∵ x + 2 is a factor of(x)
∴ Remainder = 0
∴ 4+ 4α + β = 0
⇒  4α + β = -4 …(ii)
Subtracting (i) from (ii),
2α = -2
⇒  α = \(\frac { -2 }{ 2 }\) = -1
From (ii), 4(-1) + β = -4
-4 + β= -4
⇒  β =-4+ 4 = 0
∴  α = -1, β = 0

Question 16.
If x – 2 is a factor of each of the following two polynomials, find the values of a in each case:
(i) x³ – 2ax² + ax – 1
(ii) x⁵ – 3x⁴ – ax³ + 3ax² + 2ax + 4
Solution:
(i) Let f(x) = x³ – 2ax² + ax – 1 and g(x) = x – 2
and let x – 2 = 0, then x = 2
∴ x – 2 is its factor
∴ Remainder = 0
f(2) = (2)³ – 2a x (2)² + a x 2 – 1
= 8-8a+ 2a-1 = 7-6a
∴ 7 – 6a = 0
⇒  6a = 7
⇒ a = \(\frac { 7 }{ 6 }\)
∴ a =  \(\frac { 7 }{ 6 }\)
(ii) Let f(x) = x⁵ – 3x⁴ – ax³ + 3 ax² + 2ax + 4 and g(x) = x – 2
Let x – 2 = 0, then x=2
∴ f(2) = (2)⁵ – 3(2)⁴ – a(2³) + 3a (2)² + 2a x 2 + 4
= 32 – 48 – 8a + 12a + 4a + 4
= -12 + 8a
∴ Remainder = 0
∴ -12 + 8a = 0
⇒ 8a= 12
⇒ a = \(\frac { 12 }{ 8 }\) = \(\frac { 3 }{ 2 }\)
∴ Hence a = \(\frac { 3 }{ 2 }\)

Question 17.
In each of the following two polynomials, find the values of a, if x – a is a factor:
(i) x⁶ – ax⁵ + x⁴-ax³ + 3x-a + 2
(ii) x⁵ – a²x³ + 2x + a + 1
Solution:
(i) Let f(x) ⁼ x⁶ – ax⁵+x⁴-ax³ + 3x-a + 2 and g(x) = x – a
∴ x – a is a factor
∴ x – a = 0
⇒ x = a
Now f(a) = a⁶-a x a⁵ + a⁴-a x a³ + 3a – a + 2
= a⁶-a⁶ + a⁴-a⁴ + 2a + 2
= 2a + 2
∴ x + a is a factor of p(x)
∴ Remainder = 0

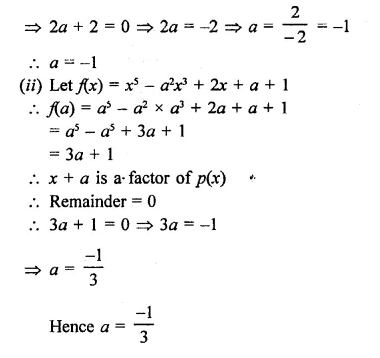
Question 18.
In each of the following, two polynomials, find the value of a, if x + a is a factor.
(i)  x³ + ax² – 2x + a + 4
(ii) x⁴ – a²r + 3x – a
Solution:

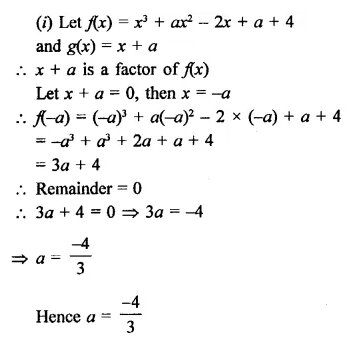
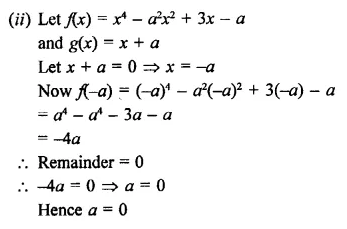
Question 19.
Find the values of p and q so that x⁴ + px³ + 2x² – 3x + q is divisible by (x² – 1).
Solution:

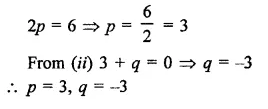
Question 20.
Find the values of a and b so that (x + 1) and (x – 1) are factors of x⁴ + ax³ 3x² + 2x + b.
Solution:

Question 21.
If x³ + ax² – bx + 10 is divisible by x² – 3x + 2, find the values of a and b.
Solution:

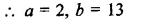
Question 22.
If both x + 1 and x – 1 are factors of ax³ + x² – 2x + b, find the values of a and b.
Solution:

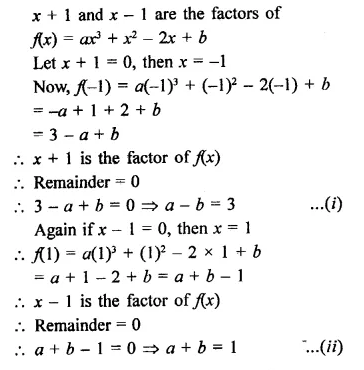
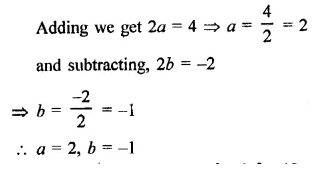
Question 23.
What must be added to x³ – 3x² – 12x + 19 so that the result is exactly divisibly by x² + x – 6?
Solution:

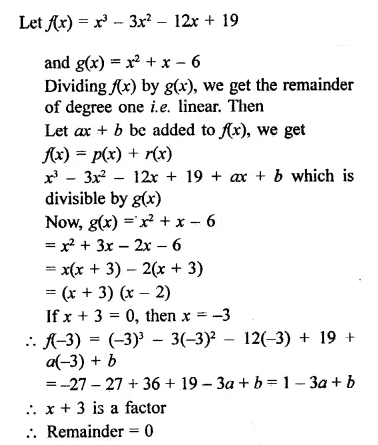
Question 24.
What must be subtracted from x³ – 6x² – 15x + 80-so that the result is exactly divisible by x² + x – 12?
Solution:

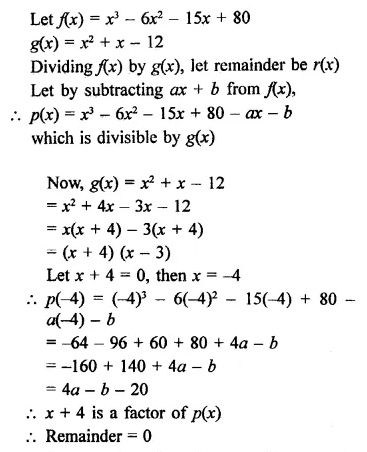
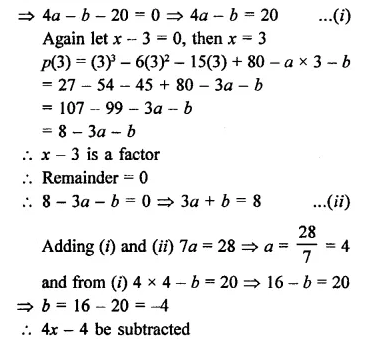
Question 25.
What must be added to 3x³ + x² – 22x + 9 so that the result is exactly divisible by 3x² + 7x – 6?
Solution:

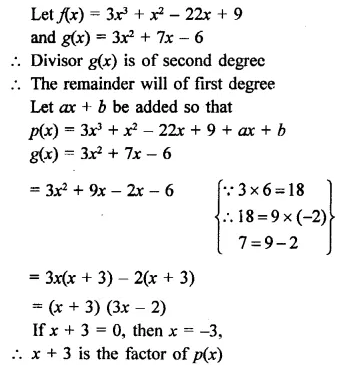
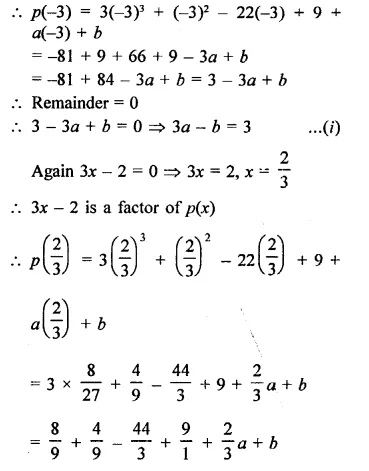
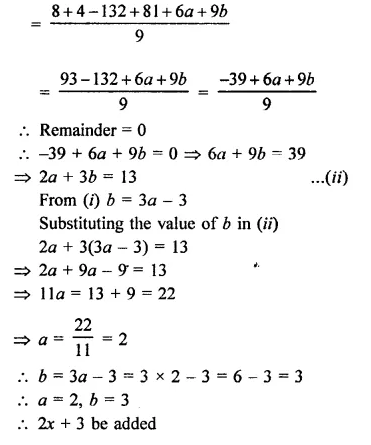
Hope given RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials Ex 6.4 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials Ex 6.2

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials Ex 6.2

Other Exercises

• RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials Ex 6.1
• RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials Ex 6.2
• RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials Ex 6.3
• RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials Ex 6.4
• RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials Ex 6.5
• RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials VSAQS
• RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials MCQS

Question 1.
If f(x) = 2x³ – 13x² + 17x + 12, find
(i) f (2)
(ii) f (-3)
(iii) f(0)
Solution:
f(x) = 2x³ – 13x² + 17x + 12
(i) f(2) = 2(2)³ – 13(2)² + 17(2) + 12
= 2 x 8-13 x 4+17 x 2+12
= 16-52 + 34 + 12
= 62 – 52
= 10
(ii) f(-3) = 2(-3)³ – 13(-3)² + 17 x (-3) + 12
= 2 x (-27) – 13 x 9 + 17 x (-3) + 12
= -54 – 117 -51 + 12
= -222 + 12
= -210
(iii) f(0) = 2 x (0)³ – 13(0)² + 17 x 0 + 12
= 0-0 + 0+ 12 = 12

Question 2.
Verify whether the indicated numbers are zeros of the polynomials corresponding to them in the following cases: [NCERT]

Solution:

Question 3.
If x = 2 is a root of the polynomial f(x) = 2x²-3x + la, find the value of a.
Solution:
p(x) = 2x² – 3x + 7a
∵ x = 2 is its zero, then
p(0) = 0
∴ p( 2) = 2(2)² – 3×2 + la = 0
⇒2 x 4-3 x2 + 7a = 0
⇒ 8 – 6 + 7o = 0
⇒2 + 7a = 0
⇒ 7a = -2 ⇒ a =\(\frac { -2 }{ 7 }\)
∴ Hence a = \(\frac { -2 }{ 7 }\)

Question 4.
If x = –\(\frac { 1 }{ 2 }\) is a zero of the polynomial p(x) = 8x³ – ax² – x + 2, find the value of a.
Solution:

Question 5.
If x = 0 and x = -1 are the roots of the polynomial f(x) = 2x³ – 3x² + ax + b, find the value of a and b.
Solution:
f(x) = 2x³ – 3x² + ax + b
∵ x = 0 and x = -1 are its zeros
∴ f(0) = 0 and f(-1) = 0
Now, f(0) = 0
⇒  2(0)³ – 3(0)² + a x 0 + b = 0
⇒ 0-0 + 0 + b= 0
∴ b = 0
and f(-1) = 0
⇒ 2(-1)³ – 3(-1)² + a(-1) + b = 0
⇒  2 x (-1) – 3 x 1 + a x (-1) + b = 0
⇒ -2 -3-a + b = 0
⇒ -2-3-a + 0 = 0
⇒ -5- a = 0=>a =-5
Hence a = -5, b = 0

Question 6.
Find the integral roots of the polynomial f(x) = x³ + 6x² + 11x + 6.
Solution:
f(x) = x³ + 6x² + 11x + 6
Construct = 6 = ±1, ±2, +3, ±6
If x = 1, then
f(1) = (1)³ + 6(1)² + 11 x 1 + 6
= 1+ 6+11+ 6 = 24
∵  f(x) ≠ 0, +0
∴ x = 1 is not its zero
Similarly, f(-1) = (-1)³ + 6(-1)² + 11(-1) + 6
= -1 + 6 x 1-11+6
=-1+6-11+6
= 12-12 = 0
∴  x = -1 is its zero
f(-2) = (-2)³ + 6(-2)² + 11 (-2) + 6
= -8 + 24 – 22 + 6
= -30 + 30 = 0
∴ x = -2 is its zero
f(-3) = (-3)³ + 6(-3)² + 11 (-3) + 6
= -27 + 54 – 33 + 6 = 60 – 60 = 0
∴  x = -3 is its zero
x = -1, -2, -3 are zeros of f(x)
Hence roots of f(x) are -1, -2, -3

Question 7.
Find the rational roots of the polynomial f(x) = 2x³ + x² – 7x – 6.
Solution:

Hope given RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials Ex 6.2 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials Ex 6.1

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials Ex 6.1

Other Exercises

• RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials Ex 6.1
• RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials Ex 6.2
• RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials Ex 6.3
• RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials Ex 6.4
• RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials Ex 6.5
• RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials VSAQS
• RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials MCQS

Question 1.
Which of the following expressions are polynomials in one variable and which are not? State reasons for your answer:

Solution:
(i) 3x² – 4x + 15,
(ii) y² + 2\(\sqrt { 3 } \) are polynomial is one variable. Others are not polynomial or polynomials in one variable.

Question 2.
Write the coefficient of x² in each of the following:

Solution:
Coefficient of x²,
in (i) is 7
in (ii) is 0 as there is no term of x² i.e. 0 x²

Question 3.
Write the degrees of each of the following polynomials:
(i) 7x³ + 4x² – 3x + 12
(ii) 12 – x + 2x³
(iii) 5y – \(\sqrt { 2 } \)
(iv) 7
(v) 0
Solution:
(i) Degree of the polynomial 7x³ + 4x² – 3x + 12 is 3
(ii) Degree of the polynomial 12 – x + 2x³ is 3
(iii) Degree of the polynomial 5y – \(\sqrt { 2 } \)is 1
(iv) Degree of the polynomial 7 is 0
(v) Degree of the polynomial 0 is 0 undefined.

Question 4.
Classify the following polynomials as linear, quadratic, cubic and biquadratic polynomials:
(i) x + x² + 4
(ii) 3x – 2
(iii) 2x + x² [NCERT]
(iv) 3y
(v) t² + 1
(v) 7t⁴ + 4t³ + 3t – 2
Solution:
(i)  x + x² + 4 It is a quadratic polynomial.
(ii) 3x – 2 : It is a linear polynomial.
(iii) 2x + x²: It is a quadratic polynomial.
(iv) 3y It is a linear polynomial.
(v) t²+ 1 It is a quadratic polynomial.
(vi) 7t⁴ + 4t³ + 3t – 2 It is a biquadratic polynomial.

Question 5.
Classify the following polynomials as polynomials in one-variable, two-variables etc.
(i) x²-xy +7y²
(ii) x² – 2tx + 7t² – x + t
(iii) t³ -3t² + 4t-5
(iv) xy + yz + zx
Solution:
(i) x² – xy + 7y²: It is a polynomial in two j variables x, y.
(ii) x² – 2tx + 7t² – x + t: It is a polynomial in two variables in x, t.
(iii) t³ – 3t² + 4t – 5 : It is a polynomial in one variable in t.
(iv) xy +yz + zx : It is a polynomial in 3 variables in x, y and

Question 6.
Identify polynomials in the following:

Solution:

Question 7.
Identify constant, linear, quadratic and cubic polynomials from the following polynomials:

Solution:
(i) f(x) = 0 : It is a constant polynomial as it has no variable.
(ii) g(x) = 2x³ – 7x + 4 : It is a cubic polynomial.
(iii) h(x) = -3x + \(\frac { 1 }{ 2 }\) : It is a linear polynomial.
(iv) p(x) = 2x² – x + 4 : It is a quadratic polynomial.
(v) q(x) = 4x + 3 : It is linear polynomial.
(vi) r(x) = 3x³ + 4x² + 5x – 7 : It is a cubic polynomial.

Question 8.
Give one example each of a binomial of degree 35 and of a monomial of degree 100.   [NCERT]
Solution:
Example of a binomial of degree 35 = 9x³⁵ + 16
Example of a monomial of degree 100 = 2y¹⁰⁰

Hope given RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials Ex 6.1 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.