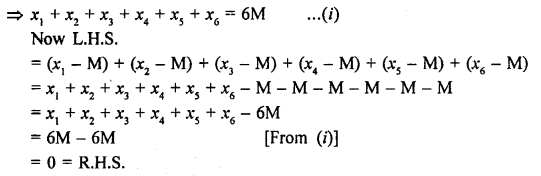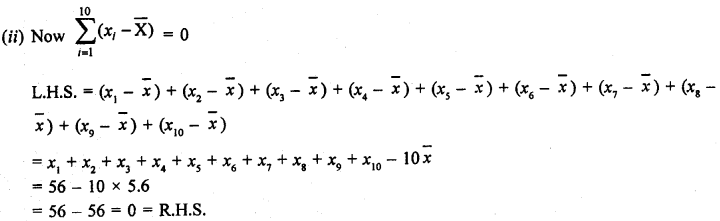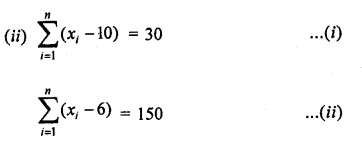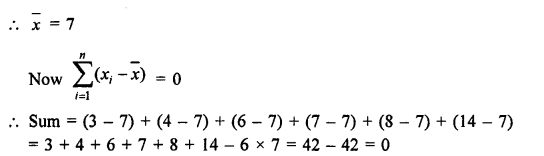Class 9 Maths RD Sharma Solutions

RD Sharma Class 9 Solutions Chapter 10 Congruent Triangles MCQS

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 10 Congruent Triangles MCQS

Other Exercises

• RD Sharma Class 9 Solutions Chapter 10 Congruent Triangles Ex 10.1
• RD Sharma Class 9 Solutions Chapter 10 Congruent Triangles Ex 10.2
• RD Sharma Class 9 Solutions Chapter 10 Congruent Triangles Ex 10.3
• RD Sharma Class 9 Solutions Chapter 10 Congruent Triangles Ex 10.4
• RD Sharma Class 9 Solutions Chapter 10 Congruent Triangles VSAQS
• RD Sharma Class 9 Solutions Chapter 10 Congruent Triangles MCQS

Mark the correct alternative in each of the following:
Question 1.
One angle is equal to three times its supplement. The measure of the angle is
(a) 130°
(b) 135°
(c) 90°
(d) 120°
Solution:
Let required angle = x
Then its supplement = (180° – x)
x = 3(180° – x) = 540° – 3x
⇒ x + 3x = 540°
⇒ 4x = 540°
⇒ x = \(\frac { { 540 }^{ \circ } }{ 4 }\)  = 135°
∴ Required angle = 135° (b)

Question 2.
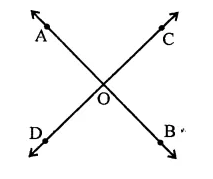
Two straight lines AB and CD intersect one another at the point O. If ∠AOC + ∠COB + ∠BOD = 274°, then ∠AOD =
(a) 86°
(b) 90°
(c) 94°
(d) 137°
Solution:
Sum of angles at a point O = 360°
Sum of three angles ∠AOC + ∠COB + ∠BOD = 274°

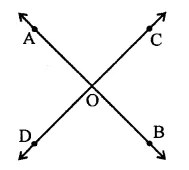
∴ Fourth angle ∠AOD = 360° – 274°
= 86° (a)

Question 3.
Two straight lines AB and CD cut each other at O. If ∠BOD = 63°, then ∠BOC =
(a) 63°
(b) 117°
(c) 17°
(d) 153°
Solution:
CD is a line
∴ ∠BOD + ∠BOC = 180° (Linear pair)

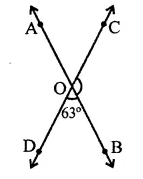
⇒ 63° + ∠BOC = 180°
⇒ ∠BOC = 180° – 63°
∴ ∠BOC =117° (b)

Question 4.
Consider the following statements:
When two straight lines intersect:
(i) adjacent angles are complementary
(ii) adjacent angles are supplementary
(iii) opposite angles are equal
(iv) opposite angles are supplementary Of these statements
(a) (i) and (iii) are correct
(b) (ii) and (iii) are correct
(c) (i) and (iv) are correct
(d) (ii) and (iv) are correct
Solution:
Only (ii) and (iii) arc true. (b)

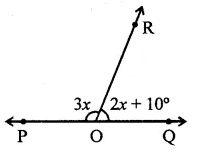
Question 5.
Given ∠POR = 3x and ∠QOR = 2x + 10°. If POQ is a striaght line, then the value of x is
(a) 30°
(b) 34°
(c) 36°
(d) none of these
Solution:
∵ POQ is a straight line
∴ ∠POR + ∠QOR = 180° (Linear pair)
⇒ 3x + 2x + 10° = 180°
⇒ 5x = 180 – 10° = 170°
∴ x = \(\frac { { 170 }^{ \circ } }{ 5 }\)  = 34° (b)

Question 6.
In the figure, AOB is a straight line. If ∠AOC + ∠BOD = 85°, then ∠COD =
(a) 85°
(b) 90°
(c) 95°
(d) 100°

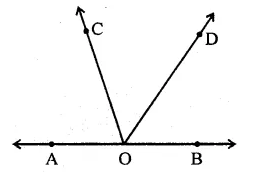
Solution:
AOB is a straight line,
OC and OD are rays on it
and ∠AOC + ∠BOD = 85°
But ∠AOC + ∠BOD + ∠COD = 180°
⇒ 85° + ∠COD = 180°
∠COD = 180° – 85° = 95° (c)

Question 7.
In the figure, the value of y is
(a) 20°
(b) 30°
(c) 45°
(d) 60°

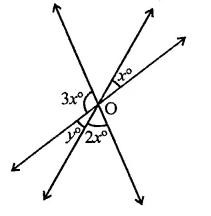
Solution:
In the figure,

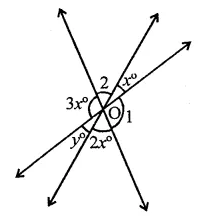
y = x (Vertically opposite angles)
∠1 = 3x
∠2 = 3x
∴ 2(x + 3x + 2x) = 360° (Angles at a point)
2x + 6x + 4x = 360°
12x = 360° ⇒ x = \(\frac { { 360 }^{ \circ } }{ 12 }\)  = 30°
∴ y = x = 30° (b)

Question 8.
In the figure, the value of x is
(a) 12
(b) 15
(c) 20
(d) 30

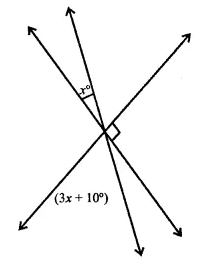
Solution:
∠1 = 3x+ 10 (Vertically opposite angles)
But x + ∠1 + ∠2 = 180°

⇒ x + 3x + 10° + 90° = 180°
⇒ 4x = 180° – 10° – 90° = 80°
x = \(\frac { { 80 }^{ \circ } }{ 4 }\) = 20   (c)

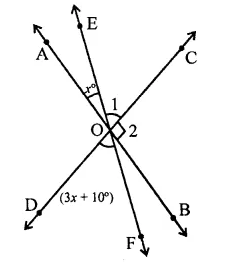
Question 9.
In the figure, which of the following statements must be true?
(i) a + b = d + c
(ii) a + c + e = 180°
(iii) b + f= c + e
(a) (i) only
(b) (ii) only
(c) (iii) only
(d) (ii) and (iii) only

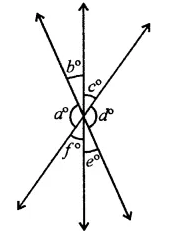
Solution:
In the figure,
(i) a + b = d + c
a° = d°
b° = e°
c°= f°
(ii) a + b + e = 180°
a + e + c = 180°
⇒ a + c + e = 180°
(iii) b + f= e + c
∴ (ii) and (iii) are true statements (d)

Question 10.
If two interior angles on the same side of a transversal intersecting two parallel lines are in the ratio 2:3, then the measure of the larger angle is
(a) 54°
(b) 120°
(c) 108°
(d) 136°
Solution:
In figure, l || m and p is transversal

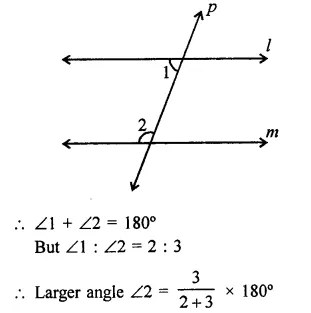
= \(\frac { 3 }{ 5 }\) x 180° = 108° (c)

Question 11.
In the figure, if AB || CD, then the value of x is
(a) 20°
(b) 30°
(c) 45°
(d) 60°

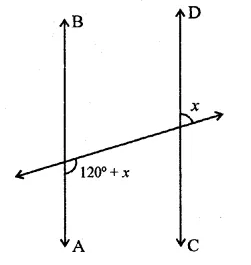
Solution:
In the figure, AB || CD,
and / is transversal
∠1 = x (Vertically opposite angles)
and 120° + x + ∠1 = 180° (Co-interior angles)

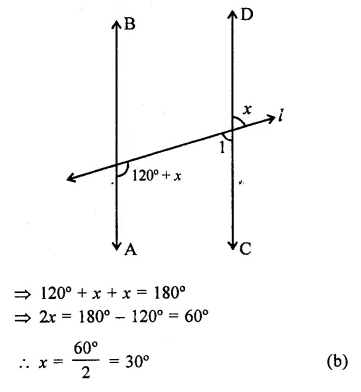
Question 12.
Two lines AB and CD intersect at O. If ∠AOC + ∠COB + ∠BOD = 270°, then ∠AOC =
(a) 70°
(b) 80°
(c) 90°
(d) 180°
Solution:
Two lines AB and CD intersect at O

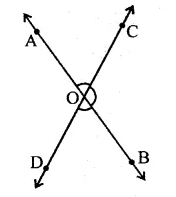
∠AOC + ∠COB + ∠BOD = 270° …(i)
But ∠AOC + ∠COB + ∠BOD + ∠DOA = 360° …(ii)
Subtracting (i) from (ii),
∠DOA = 360° – 270° = 90°
But ∠DOA + ∠AOC = 180°
∴ ∠AOC = 180° – 90° = 90° (c)

Question 13.
In the figure, PQ || RS, ∠AEF = 95°, ∠BHS = 110° and ∠ABC = x°. Then the value of x is
(a) 15°
(b) 25°
(c) 70°
(d) 35°

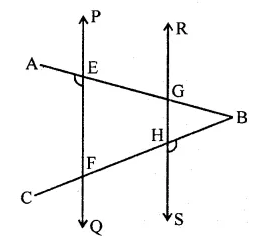
Solution:
In the figure,

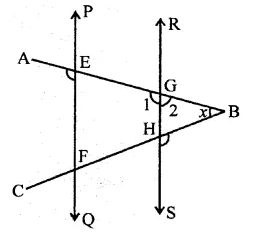
PQ || RS, ∠AEF = 95°
∠BHS = 110°, ∠ABC = x
∵ PQ || RS,
∴ ∠AEF = ∠1 = 95° (Corresponding anlges)
But ∠1 + ∠2 = 180° (Linear pair)
⇒ ∠2 = 180° – ∠1 = 180° – 95° = 85°
In ∆AGH,
Ext. ∠BHS = ∠2 +x
⇒ 110° = 85° + x
⇒ x= 110°-85° = 25° (b)

Question 14.
In the figure, if l1 || l2, what is the value of x?
(a) 90°
(b) 85°
(c) 75°
(d) 70°

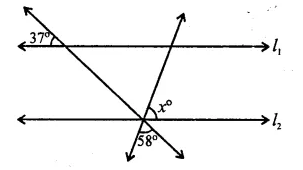
Solution:
In the figure,

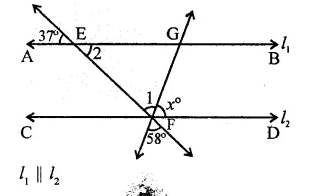
∠1 = 58° (Vertically opposite angles)
Similarly, ∠2 = 37°
∵ l₁ || l₂, EF is transversal
∠GEF + EFD = 180° (Co-interior angles)
⇒ ∠2 + ∠l +x = 180°
⇒ 37° + 58° + x = 180°
⇒ 95° + x= 180°
x = 180°-95° = 85° (b)

Question 15.
In the figure, if l₁ || l₂, what is x + y in terms of w and z?
(a) 180-w + z
(b) 180° + w- z
(c) 180 -w- z
(d) 180 + w + z

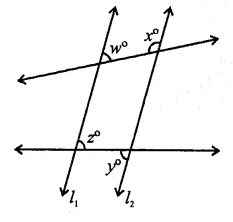
Solution:
In the figure, l₁ || l₂

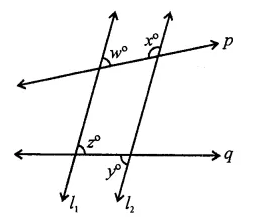
p and q are transversals
∴ w + x = 180° ⇒ x = 180° – w (Co-interior angle)
z = y (Alternate angles)
∴ x + y = 180° – w + z (a)

Question 16.
In the figure, if l₁ || l₂, what is the value of y?
(a) 100
(b) 120
(c) 135
(d) 150

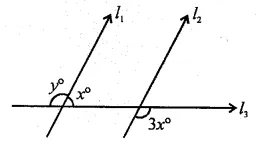
Solution:
In the figure, l₁ || l₂ and l₃ is the transversal

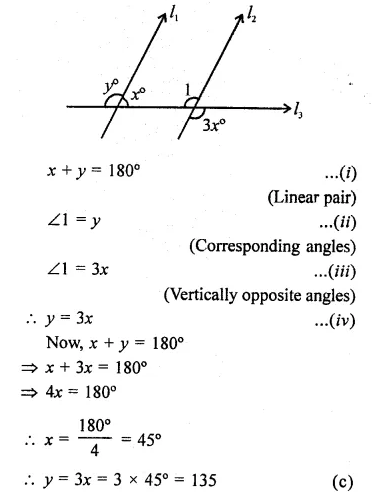
Question 17.
In the figure, if l1 || l2 and l3 || l4 what is y in terms of x?
(a) 90 + x
(b) 90 + 2x
(c) 90 – \(\frac { x }{ 2 }\)
(d) 90 – 2x

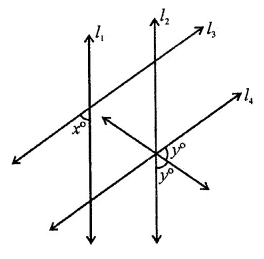
Solution:
In the figure,

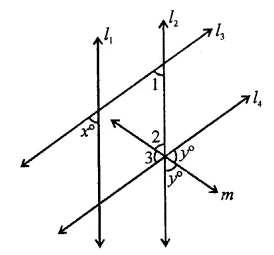
l₁ || l₂ and l₃ || l₄ and m is the angle bisector
∴ ∠2 = ∠3 = y
∵ l₁ || l₂
∠1 = x (Corresponding angles)
∵ l₃ || l₄
∴ ∠1 + (∠2 + ∠3) = 180° (Co-interior angles)
⇒ x + 2y= 180°
⇒ 2y= 180°-x
⇒ y = \(\frac { { 540 }^{ \circ }-x }{ 4 }\)
= 90° – \(\frac { x }{ 2 }\) (c)

Question 18.
In the figure, if 11| m, what is the value of x?
(a) 60
(b) 50
(c) 45
d) 30

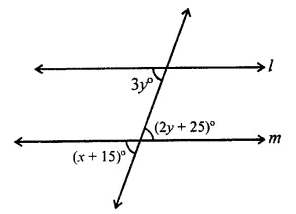
Solution:
In the figure, l || m and n is the transversal

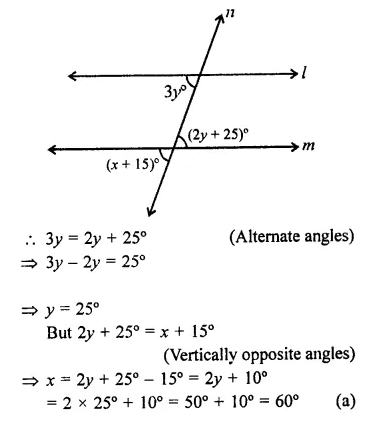
⇒ y = 25°
But 2y + 25° = x+ 15°
(Vertically opposite angles) ⇒ x = 2y + 25° – 15° = 2y+ 10°
= 2 x 25°+10° = 50°+10° = 60° (a)

Question 19.
In the figure, if AB || HF and DE || FG, then the measure of ∠FDE is
(a) 108°
(b) 80°
(c) 100°
(d) 90°

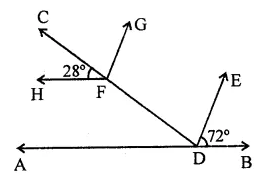
Solution:
In the figure,
AB || HF, DE || FG

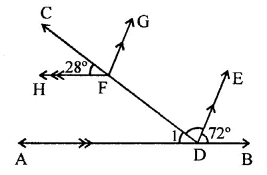
∴ HF || AB
∠1 =28° (Corresponding angles)
But ∠1 + ∠FDE + 72° – 180° (Angles of a straight line)
⇒ 28° + ∠FDE + 72° = 180°
⇒ ∠FDE + 100° = 180°
⇒ ∠FDE = 180° – 100 = 80° (b)

Question 20.
In the figure, if lines l and m are parallel, then x =
(a) 20°
(b) 45°
(c) 65°
(d) 85°

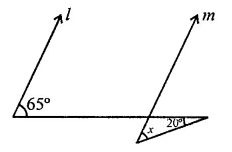
Solution:
In the figure, l || m

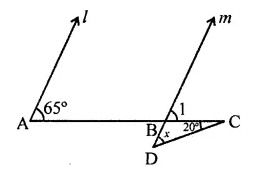
∴ ∠1 =65° (Corresponding angles)
In ∆BCD,
Ext. ∠1 = x + 20°
⇒ 65° = x + 20°
⇒ x = 65° – 20°
⇒ x = 45° (b)

Question 21.
In the figure, if AB || CD, then x =
(a) 100°
(b) 105°
(c) 110°
(d) 115°

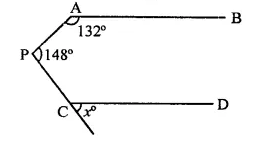
Solution:
In the figure, AB || CD
Through P, draw PQ || AB or CD

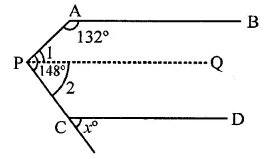
∠A + ∠1 = 180° (Co-interior angles)
⇒ 132° + ∠1 = 180°
⇒ ∠1 = 180°- 132° = 48°
∴ ∠2 = 148° – ∠1 = 148° – 48° = 100°
∵ DQ || CP
∴ ∠2 = x (Corresponding angles)
∴ x = 100° (a)

Question 22.
In tlie figure, if lines l and in are parallel lines, then x =
(a) 70°
(b) 100°
(c) 40°
(d) 30°

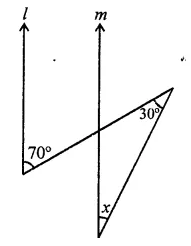
Solution:
In the figure, l || m

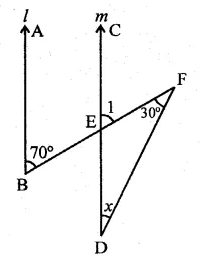
∠l =70° (Corresponding angles)
In ∆DEF,
Ext. ∠l = x + 30°
⇒ 70° = x + 30°
⇒ x = 70° – 30° = 40° (c)

Question 23.
In the figure, if l || m, then x =
(a) 105°
(b) 65°
(c) 40°
(d) 25°

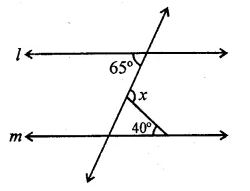
Solution:
In the figure,
l || m and n is the transversal

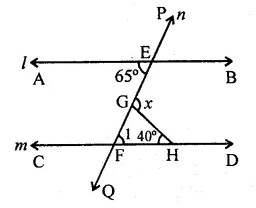
∠1 = 65° (Alternate angles)
In ∆GHF,
Ext. x = ∠1 + 40° = 65° + 40°
⇒ x = 105°
∴ x = 105° (a)

Question 24.
In the figure, if lines l and m are parallel, then the value of x is
(a) 35°
(b) 55°
(c) 65°
(d) 75°

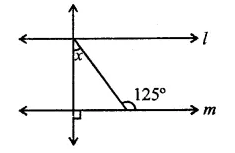
Solution:
In the figure, l || m
and PQ is the transversal

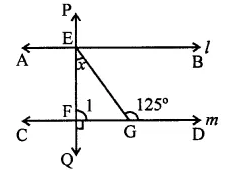
∠1 = 90°
In ∆EFG,
Ext. ∠G = ∠E + ∠F
⇒ 125° = x + ∠1 = x + 90°
⇒ x = 125° – 90° = 35° (a)

Question 25.
Two complementary angles are such that two times the measure of one is equal to three times the measure of the other. The measure of the smaller angle is
(a) 45°
(b) 30°
(c) 36°
(d) none of these
Solution:
Let first angle = x
Then its complementary angle = 90° – x
∴ 2x = 3(90° – x)
⇒ 2x = 270° – 3x
⇒ 2x + 3x = 270°
⇒ 5x = 270°
⇒ x = \(\frac { { 270 }^{ \circ } }{ 5 }\)  = 54°
∴ second angle = 90° – 54° = 36°
∴ smaller angle = 36° (c)

Question 26.

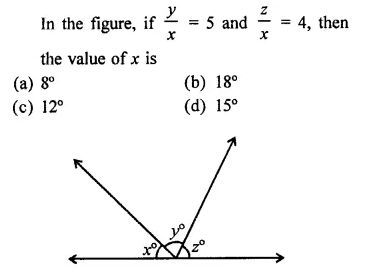
Solution:

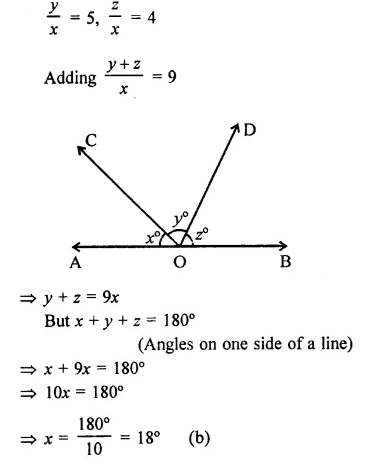
Question 27.
In the figure, AB || CD || EF and GH || KL.
The measure of ∠HKL is
(a) 85°
(b) 135°
(c) 145°
(d) 215°

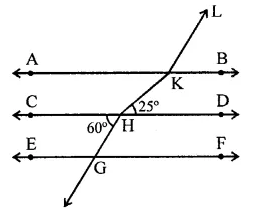
Solution:
In the figure, AB || CD || EF and GH || KL and GH is product to meet AB in L.

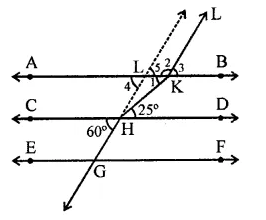
∵ AB || CD
∴ ∠1 = 25° (Alternate angle)
and GH || KL
∴ ∠4 = 60° (Corresponding angles)
∠5 = ∠4 = 60° (Vertically opposite angle)
∠5 + ∠2 = 180° (Co-interior anlges)
∴ ⇒ 60° + ∠2 = 180°
∠2 = 180° – 60° = 120°
Now ∠HKL = ∠1 + ∠2 = 25° + 120°
= 145° (c)

Question 28.
AB and CD are two parallel lines. PQ cuts AB and CD at E and F respectively. EL is the bisector of ∠FEB. If ∠LEB = 35°, then ∠CFQ will be
(a) 55°
(b) 70°
(c) 110°
(d) 130°
Solution:
AB || CD and PQ is the transversal EL is the bisector of ∠FEB and ∠LEB = 35°

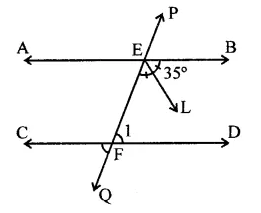
∴ ∠FEB = 2 x 35° = 70°
∵ AB || CD
∴ ∠FEB + ∠EFD = 180°
(Co-interior angles)
70° + ∠EFD = 180°
∴ ∠EFD = 180°-70°= 110°
But ∠CFQ = ∠EFD
(Vertically opposite angles)
∴ ∠CFQ =110° (c)

Question 29.
In the figure, if line segment AB is parallel to the line segment CD, what is the value of y?
(a) 12
(b) 15
(c) 18
(d) 20

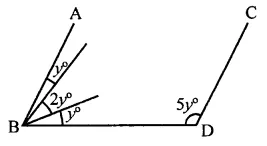
Solution:
In the figure, AB || CD
BD is transversal
∴ ∠ABD + ∠BDC = 180° (Co-interior angles)
⇒y + 2y+y + 5y = 180°
⇒ 9y = 180° ⇒ y = \(\frac { { 180 }^{ \circ } }{ 9 }\)  = 20° (d)

Question 30.
In the figure, if CP || DQ, then the measure of x is
(a) 130°
(b) 105°
(c) 175°
(d) 125°

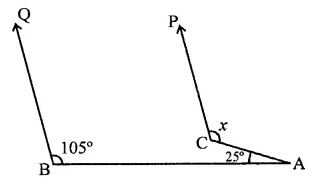
Solution:
In the figure, CP || DQ
BA is transversal
Produce PC to meet BA at D

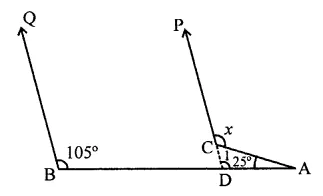
∵ QB || PD
∴ ∠D = 105° (Corresponding angles)
In ∆ADC,
Ext. ∠ACP = ∠CDA + ∠DAC
⇒ x = ∠1 + 25°
= 105° + 25° = 130° (a)

Hope given RD Sharma Class 9 Solutions Chapter 10 Congruent Triangles MCQS are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 9 Solutions Chapter 24 Measures of Central Tendency Ex 24.1

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 24 Measures of Central Tendency Ex 24.1

Other Exercises

• RD Sharma Class 9 Solutions Chapter 24 Measures of Central Tendency Ex 24.1
• RD Sharma Class 9 Solutions Chapter 24 Measures of Central Tendency Ex 24.2
• RD Sharma Class 9 Solutions Chapter 24 Measures of Central Tendency Ex 24.3
• RD Sharma Class 9 Solutions Chapter 24 Measures of Central Tendency Ex 24.4
• RD Sharma Class 9 Solutions Chapter 24 Measures of Central Tendency VSAQS
• RD Sharma Class 9 Solutions Chapter 24 Measures of Central Tendency MCQS

Question 1.
If the heights of 5 persons are 140 cm, 150 cm, 152 cm, 158 cm and 161 cm respectively. Find the mean height.
Solution:
Heights of 5 persons are 140 cm, 150 cm, 152 cm, 158 cm and 161 cm

Question 2.
Find the mean of 994, 996, 998, 1002 and 1000.
Solution:
Mean of 994, 996, 998, 1002 and 1000

Question 3.
Find the mean of first five natural numbers.
Solution:
First five natural numbers are 1, 2, 3, 4, 5
∴ Mean = \(\overline { x } =\frac { 1+2+3+4+5 }{ 5 } =\frac { 15 }{ 5 } \) = 3

Question 4.
Find the mean all factors of 10.
Solution:
Factors of 10 = 1, 2, 5, 10
∴ Mean = \(\overline { x } =\frac { 1+2+5+10 }{ 4 } =\frac { 18 }{ 4 } \) = 4.5

Question 5.
Find the mean of first 10 even natural numbers.
Solution:
First 10 even natural numbers are 2, 4, 6, 8, 10, 12, 14, 16, 18, 20
∴ Mean = \(\overline { x } =\frac { 2+4+6+8+10+12+14+16+18+20 }{ 10 } =\frac { 110 }{ 10 } \) = 11

Question 6.
Find the mean of x, x + 2, x + 4, x + 6, x + 8.
Solution:
Sum = x + x + 2+ x + 4 + x + 6 + x + 8 = 5x + 20
∴ Mean = \(\overline { x } =\frac { \sum { { x }_{ i } } }{ n } \frac { 5x+20 }{ 5 } =x+4 \)

Question 7.
Find the mean of first five multiples of 3.
Solution:
First 5 multiples of 3 are = 3, 6, 9, 12, 15
∴ Mean = \(\overline { x } =\frac { 3+6+9+12+15 }{ 5 } =\frac { 45 }{ 5 } \) = 9

Question 8.
Following are the weights (in kg) or 10 new born babies in a hospital on a particular day:
3.4, 3.6, 4.2, 4.5, 3.9, 4.1, 3.8, 4.5, 4.4, 3.6. Find the mean \(\overline { X } \).
Solution:
Weights of 10 new bom babies are 3.4, 3.6, 4.2, 4.5, 3.9, 4.1, 3.8, 4.5, 4.4, 3.6
∴ Mean \(\overline { X } \) = \(\frac { 3.4+3.6+4.2+4.5+3.9+4.1+3.8+4.5+4.4+3.6 }{ 10 } \)
= \(\frac { 40.0 }{ 10 } \) = 4kg

Question 9.
The percentage of marks obtained by students of a class in mathematics are : 64, 36, 47, 23, 0, 19, 81, 93, 72, 35, 3, 1. Find their mean.
Solution:
Percentage of 12 students are 64, 36, 47, 23, 0, 19, 81, 93, 72, 35, 3, 1
∴ Mean \(\overline { X } \) = \(\frac { 64+36+47+23+0+19+81+93+72+35+3+1 }{ 12 } \)
= \(\frac { 474 }{ 12 } \) = 39.5

Question 10.
The numbers of children in 10 families of a locality are : 2, 4, 3, 4, 2, 0, 3, 5, 1, 1, 5. Find the mean number of children per family.
Solution:
Number of children in 10 families are 2, 4, 3, 4, 2, 0, 3, 5, 1, 1, 5
∴ Mean \(\overline { X } \) = \(\frac { 2+4+3+4+2+0+3+5+1+1+5 }{ 10 } \)
= \(\frac { 30 }{ 10 } \) = 3

Question 11.
Explain, by taking a suitable example, how the arithmetic mean alters by (i) adding a constant k to each term, (ii) subtracting a constant k from each them, (iii) multiplying each term by a constant k and (iv) dividing each term by a non-zero constant k.
Solution:
Let x1, x2, x3, x4, x5 are five numbers whose mean is \(\overline { x } \) i.e. = \(\frac { x1+x2+x3+x4+x5 }{ 5 } \) = \(\overline { x } \)


Hence we see that in each case, the mean is changed.

Question 12.
The mean of marks scored by 100 students was found to be 40. Later on its was discovered that a score of 53 was misread as 83. Find the correct mean.
Solution:
Mean score of 100 students = 40
∴Total = 100 x 40 = 4000
Difference in one score by mistake = 83 – 53 = 30
Actual total scores = 4000 – 300 = 3970
Actual mean = \(\frac { 3970 }{ 100 } \) = 39.70 = 39.7

Question 13.
The traffic police recorded the speed (in km/hr) of 10 motorists as 47, 53, 49, 60, 39, 42, 55, 57, 52, 48. Later on an error in recording instrument was found. Find the correct average speed of the motorists if the instrument recorded 5 km/hr less in each case.
Solution:
Speed of 10 motorist as recorded = 47, 53, 49, 60, 39, 42, 55, 57, 52, 48
Total of speed of 10 motorists = 47 + 53 + 49 + 60 + 39 + 42 + 55 +57 + 52 + 48 = 502

Question 14.
The mean of five numbers is 27. If one number is excluded, their mean is 25. Find the excluded number.
Solution:
Mean of 5 numbers = 27
Total = 27 x 5 = 135
By excluded one number, then mean of remaining 4 numbers = 25
Total = 4 x 25 = 100
Excluded number = 135 – 100 = 35

Question 15.
The mean weight per student in a group of 7 students is 55 kg. The individual weights of 6 of them (in kg) are 52, 54, 55, 53, 56 and 54. Find the weight of the seventh student.
Solution:
Mean weight of 7 students = 55 kg
Total weight of 7 students = 55 x 7 kg = 385 kg
Total weights of 6 students among them = 52 + 54 + 55 + 53 + 56 + 54 = 324 kg
Weight of 7th student = 385 – 324 = 61 kg

Question 16.
The mean weight of 8 numbers is 15. If each number is multiplied by 2, what will be the new mean?
Solution:
Weight of 8 numbers =15
By multiplying each number by 2, then the average will be = 15 x 2 = 30
New average = 30

Question 17.
The mean of 5 numbers is 18. If one number is excluded, their mean is 16. Find the excluded number.
Solution:
Mean of 5 numbers = 18
Total = 18 x 5 = 90
By excluding one number, the mean of remaining 5 – 1=4 numbers = 16
Total = 16 x 4 = 64
Excluded number = 90 – 64 = 26

Question 18.
The mean of 200 items was 50. Later on, it was discovered that the two items were misread as 92 and 8 instead of 192 and 88. Find the correct mean.
Solution:
Mean of 200 items = 50
Total = 50 x 200 = 10000
The number were misread as 92 instead of 192 and 8 instead of 88
Difference = 192 – 92 + 88 – 8 = 180
New total = 10000 + 180 = 10180
and new mean = \(\frac { 10180 }{ 200 } \) = 50.9

Question 19.
If M is the mean of x1, x2, xr3, x4, x5 and x6, prove that
(x1 – M) + (x2 – M) + (x3 – M) + (x4 – M) + (x5 – M) + (x6 – M) = 0.
Solution:
∵ M is the mean of x,, x2, x3, x4, x5, x6
Then M = \(\frac { x1+x2+x3+x4+x5+x6 }{ 6 } \)

Question 20.
Durations of sunshine (in hours) in Amritsar for first 10 days of August 1997 as reported by the Meteorological Department are given below:
9.6, 5.2, 3.5, 1.5, 1.6, 2.4, 2.6, 8.4, 10.3, 10.9
(i) Find the mean \(\overline { X }\)
(ii) Verify that \( \sum _{ i=1 }^{ 10 }{ \left( { x }_{ i }-\overline { X } \right) } \) = 0
Solution:
Duration of sun shine for 10 days (in hours)
= 9.6, 5.2, 3.5, 1.5, 1.6, 2.4, 2.6, 8.4, 10.3, 10.9

Question 21.
Find the values of n and X in each of the following cases:
(i) \(\sum _{ i=1 }^{ n }{ \left( { x }_{ i }-12 \right) } =-10\quad and\sum _{ i=1 }^{ n }{ \left( { x }_{ i }-3 \right) } =62\)
(ii) \(\sum _{ i=1 }^{ n }{ \left( { x }_{ i }-10 \right) } =30\quad and\sum _{ i=1 }^{ n }{ \left( { x }_{ i }-6 \right) } =150\)
Solution:
(i) \(\sum _{ i=1 }^{ n }{ \left( { x }_{ i }-12 \right) } =-10\)…(i)

Question 22.
The sums of the deviations of a set of n values x1, x2,… xn measured from 15 and -3 are -90 and 54 respectively. Find the value of n and mean.
Solution:
In first case,
(x1 – 15) + (x2 – 15) + (x3 – 15) + … + (xn – 15) = – 90
=> x1 + x2 + x3 + … + xn – 15 x n = – 90

Question 23.
Find the sum of the deviations of the variate values 3, 4, 6, 7, 8, 14 from their mean.
Solution:
Mean of 3, 4, 6, 7, 8, 14 = \(\frac { 42 }{ 6 } \) = 7

Question 24.
If \(\overline { X } \) is the mean of the ten natural numbers x1, x2, x3, …, x10, show that (x1 – \(\overline { X } \)) + (x2 – \(\overline { X } \)) + … + (x10 – \(\overline { X } \)) = 0.
Solution:
\(\overline { X } \) is the mean of 10 natural numbers
x1, x2, x3, …, x10

Hope given RD Sharma Class 9 Solutions Chapter 24 Measures of Central Tendency Ex 24.1 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 9 Solutions Chapter 10 Congruent Triangles VSAQS

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 10 Congruent Triangles VSAQS

Other Exercises

• RD Sharma Class 9 Solutions Chapter 10 Congruent Triangles Ex 10.1
• RD Sharma Class 9 Solutions Chapter 10 Congruent Triangles Ex 10.2
• RD Sharma Class 9 Solutions Chapter 10 Congruent Triangles Ex 10.3
• RD Sharma Class 9 Solutions Chapter 10 Congruent Triangles Ex 10.4
• RD Sharma Class 9 Solutions Chapter 10 Congruent Triangles VSAQS
• RD Sharma Class 9 Solutions Chapter 10 Congruent Triangles MCQS

Question 1.
Define complementary angles.
Solution:
Two angles whose sum is 90°, are called complementary angles.

Question 2.
Define supplementary angles.
Solution:
Two angles whose sum is 180°, are called supplementary angles.

Question 3.
Define adjacent angles.
Solution:
Two angles which have common vertex and one arm common are called adjacent angles.

Question 4.
The complement of an acute angles is…….
Solution:
The complement of an acute angles is an acute angle.

Question 5.
The supplement of an acute angles is………
Solution:
The supplement of an acute angles is a obtuse angle.

Question 6.
The supplement of a right angle is…….
Solution:
The supplement of a right angle is a right angle.

Question 7.
Write the complement of an angle of measure x°.
Solution:
The complement of x° is (90° – x)°

Question 8.
Write the supplement of an angle of measure 2y°.
Solution:
The supplement of 2y° is (180° – 2y)°

Question 9.
If a wheel has six spokes equally spaced, then find the measure of the angle between two adjacent spokes.
Solution:
Total measure of angle around a point = 360°
Number of spokes = 6
∴ Angle between the two adjacent spokes = \(\frac { { 360 }^{ \circ } }{ 6 }\) = 60°

Question 10.
An angle is equal to its supplement. Determine its measure.
Solution:
Let required angle = x°
Then its supplement angle = 180° – x
x = 180° – x
⇒ x + x = 180°
⇒  2x = 180° ⇒  x = \(\frac { { 180 }^{ \circ } }{ 2 }\) = 90°
∴ Required angle = 90°

Question 11.
An angle is equal to five times its complement. Determine its measure.
Solution:
Let required measure of angle = x°
∴  Its complement angle = 90° – x
∴  x = 5(90° – x)
⇒  x = 450° – 5x
⇒  x + 5x = 450°
⇒  6x = 450°
⇒ x = \(\frac { { 450 }^{ \circ } }{ 6 }\) = 75°
∴ Required angle = 75°

Question 12.
How many pairs of adjacent angles are formed when two lines intersect in a point?
Solution:
If two lines AB and CD intersect at a point O, then pairs of two adjacent angles are, ∠AOC and ∠COB, ∠COB and ∠BOD, ∠BOD and DOA, ∠DOA and ∠ZAOC
i.e, 4 pairs

Hope given RD Sharma Class 9 Solutions Chapter 10 Congruent Triangles VSAQS are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 9 Solutions Chapter 25 Probability MCQS

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 25 Probability MCQS

Other Exercises

• RD Sharma Class 9 Solutions Chapter 25 Probability Ex 25.1
• RD Sharma Class 9 Solutions Chapter 25 Probability VSAQS
• RD Sharma Class 9 Solutions Chapter 25 Probability MCQS

Mark the correct alternative in each of the following:

Question 1.
The probability of an impossible event is
(a) 1
(b) 0
(c) less than 0
(d) greater than 1
Solution:
The probability of an impossible event is 0 (b)

Question 2.
The probability on a certain event is
(a) 0
(b) 1
(c) greater than 1
(d) less than 1
Solution:
The probability of a certain event is 1 (b)

Question 3.
The probability of an event of a trial is
(a) 1
(b) 0
(c) less than 1
(d) more than 1
Solution:
The probability of an even of a trial is less than 1 (c)

Question 4.
Which of the following cannot be the probability of an event?
(a) \(\frac { 1 }{ 3 } \)
(b) \(\frac { 3 }{ 5 } \)
(c) \(\frac { 5 }{ 3 } \)
(d) 1
Solution:
The probability of an event is less than 1
\(\frac { 5 }{ 3 } \) i.e .\(1\frac { 2 }{ 3 } \) is not the probability

Question 5.
Two coins are tossed simultaneously. The probability of getting atmost one head is
(a) \(\frac { 1 }{ 4 } \)
(b) \(\frac { 3 }{ 4 } \)
(c) \(\frac { 1 }{ 2 } \)
(d) \(\frac { 1 }{ 4 } \)
Solution:
Total number of possible events (n) = 2 + 2 = 4
Number of events coming at the most 1 head (m) 2 times + 1 times = 3
Probability P(A) = \(\frac { m }{ n } \) = \(\frac { 3 }{ 4 } \) (b)

Question 6.
A coin is tossed 1000 times, if the probability of getting a tail is 3/8, how many times head is obtained?
(a) 525
(b) 375
(c) 625
(d) 725
Solution:
No. of times a coin is tossed (n) = 1000
Probability of getting a tail = \(\frac { 3 }{ 8 } \)
Let No. of tail come = x
Probability P(A) = \(\frac { m }{ n } =\frac { x }{ 1000 } \)
\(\frac { x }{ 1000 } \) = \(\frac { 3 }{ 8 } \)
=> \(\frac { x }{ 1000 } =\frac { 3 }{ 8 } \) => \(\frac { 3X1000 }{ 8 } =3X125\)
=> x = 375
∴ No. of heads are obtained = 1000 – 375 = 625 (c)

Question 7.
A dice is rolled 600 times and the occurrence of the outcomes 1, 2, 3, 4, 5 and 6 are given below:

The probability of getting a prime number is
(a)\(\frac { 1 }{ 3 } \)
(b)\(\frac { 2 }{ 3 } \)
(c)\(\frac { 49 }{ 60 } \)
(d)\(\frac { 39 }{ 125 } \)
Solution:
Total number of times a dice is rolled (n) = 600

Now total number of times getting a prime number i.e. 2, 3, 5, (m) = 30 + 120 + 50 = 200
Probability P(A) = \(\frac { m }{ n } \) = \(\frac { 200 }{ 600 } \) = \(\frac { 1 }{ 3 } \) (a)

Question 8.
The percentage of attendance of different classes in a year in a school is given below:

What is the probability that the class attendance is more than 75%?
(a) \(\frac { 1 }{ 6 } \)
(b) \(\frac { 1 }{ 3 } \)
(c) \(\frac { 5 }{ 6 } \)
(d) \(\frac { 1 }{ 2 } \)
Solution:
Percentage of attendance of different classes

Total attendance more than 75% (m) VIII,VII and VI = 3 classes
and total number of classes (n) = 6
Probability P(A) = \(\frac { 3 }{ 6 } \) = \(\frac { 1 }{ 2 } \).

Question 9.
A bag contains 50 coins and each coin is marked from 51 to 100. One coin is picked at random.
The probability that the number on the coin is not a prime number, is
(a) \(\frac { 1 }{ 5 } \)
(b) \(\frac { 3 }{ 5 } \)
(c) \(\frac { 2 }{ 5 } \)
(d) \(\frac { 4 }{ 5 } \)
Solution:
Total number of coins (n) = 50
Prime numbers between 51 to 100 are 53, 59, 6, 67, 71, 73, 79, 83, 89, 97 = 10
Numbers which are not primes (m) = 50 – 10 = 40
Probability P(A) = \(\frac { m }{ n } \) = \(\frac { 40 }{ 50 } \) = \(\frac { 4 }{ 5 } \)(d)

Question 10.
In a football match, Ronaldo makes 4 pals from 10 penalty kids. The probability of converting a penalty kick into a goal by Ronaldo,is
(a) \(\frac { 1 }{ 4 } \)
(b) \(\frac { 1 }{ 6 } \)
(c) \(\frac { 1 }{ 3 } \)
(d) \(\frac { 2 }{ 5 } \)
Solution:
No. of penalty kicks (n) = 10
No. of goal scored (m) = 4
Probability of converting a penally Into goals P(A) = \(\frac { 4 }{ 10 } \) = \(\frac { 2 }{ 5 } \)(d)

Hope given RD Sharma Class 9 Solutions Chapter 25 Probability MCQS are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 9 Solutions Chapter 25 Probability VSAQS

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 25 Probability VSAQS

Other Exercises

• RD Sharma Class 9 Solutions Chapter 25 Probability Ex 25.1
• RD Sharma Class 9 Solutions Chapter 25 Probability VSAQS
• RD Sharma Class 9 Solutions Chapter 25 Probability MCQS

Question 1.
Define a trial.
Solution:
When we perform an experiment, it is called a trial of the experiment.

Question 2.
Define an elementary event.
Solution:
An outcome of a trial of an experiment is called an elementary event.

Question 3.
Define an event.
Solution:
An event association to a random experiment is said to occur in a trial.

Question 4.
Define probability of an event.
Solution:
In n trials of a random experiment if an event A happens m times, then probability of happening
of A is given by P(A) = \(\frac { m }{ n } \)

Question 5.
A bag contains 4 white balls and some red balls. If the probability of drawing a white ball from the bag is \(\frac { 2 }{ 5 } \), find the number of red balls in the bag
Solution:
No. of white balls = 4
Let number of red balls = x
Then total number of balls (n) = 4 white + x red = (4 + x) balls

Question 6.
A die is thrown 100 times. If the probability of getting an even number is \(\frac { 2 }{ 5 } \). How many times an odd number is obtained?
Solution:
Total number of a die is thrown = 100
Let an even number comes x times, then probability of an even number = \(\frac { x }{ 100 } \)

Question 7.
Three coins are tossed simultaneously 200 times with the following frequencies of different outcomes

Find the probability of getting at most two heads.
Solution:
Total number of three coins are tossed (n) = 200
Getting at the most 2 heads (m) = 72 + 77 + 28 = 177
Probability P(A) = \(\frac { m }{ n } \) = \(\frac { 177 }{ 200 } \)

Question 8.
In the Q. No. 7, what is the probability of getting at least two heads?
Solution:
Total number of possible events = 200
No. of events getting at the least = 2 heads (m) = 23 + 72 = 95
Probability P(A) = \(\frac { m }{ n } \) = \(\frac { 95 }{ 200 } \) = \(\frac { 19 }{ 40 } \)

Hope given RD Sharma Class 9 Solutions Chapter 25 Probability VSAQS are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.