RS Aggarwal Class 9 Solutions Chapter 5 Congruence of Triangles and Inequalities in a Triangle Ex 5A
These Solutions are part of RS Aggarwal Solutions Class 9. Here we have given RS Aggarwal Class 9 Solutions Chapter 5 Congruence of Triangles and Inequalities in a Triangle Ex 5A.
Question 1.
Solution:
In ∆ ABC, ∠A = 70° and AB = AC (given)
∴ ∠C = ∠B
(Angles opposite to equal sides)
But ∠A + ∠B + ∠C = 180°
(Sum of angles of a triangle)
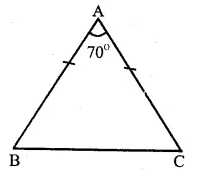
=> 70° + ∠B + ∠B = 180°
(∴ ∠B = ∠C)
=> 2∠B = 180°- 70° = 110°
∠B = \(\frac { { 110 }^{ o } }{ 2 } \) = 55° and
Hence ∠B = 55°,∠C = 55° Ans.
Question 2.
Solution:
In ∆ ABC, ∠A= 100°
It is an isosceles triangle
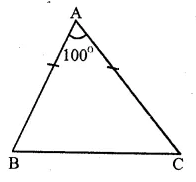
∴AB = AC
∠B = ∠C
(Angles opposite to equal sides)
But ∠A + ∠B + ∠C = 180°
(Sum of angles of a triangle)
=> 100° + ∠B + ∠B = 180°
(∴ ∠B = ∠C)
=> 2∠B + 100° = 180°
=> 2∠B = 180°- 100° = 80°
∠B = \(\frac { { 80 }^{ o } }{ 2 } \) = 40°
and ∠C = 40°
∴ Base angles are 40°, 40° Ans.
Question 3.
Solution:
In ∆ ABC,
AB = AC
∴∠C = ∠B
(Angles opposite to equal sides)
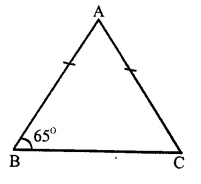
But ∠B = 65°
∴ ∠ C = 65°
But ∠A + ∠B + ∠C = 180°
(Sum of angles of a triangle)
=> ∠A + 65° + 65° = 180°
=> ∠ A + 130° = 180°
=> ∠ A = 180° – 130°
=> ∠ A = 50°
Hence ∠ A = 50° and ∠ C = 65° Ans.
Question 4.
Solution:
In ∆ ABC
AB = AC
∴ ∠C = ∠B
(Angles opposite to equal sides)
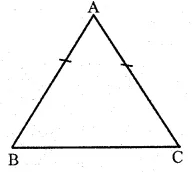
But ∠A = 2(∠B + ∠C)
=> ∠B + ∠C = \(\frac { 1 }{ 2 } \) ∠A 2
But ∠A + ∠B + ∠C = 180°
(sum of angles of a triangle)
=> ∠A+ \(\frac { 1 }{ 2 } \) ∠A = 180°
=> \(\frac { 3 }{ 2 } \) ∠A = 180°
=> ∠A = 180° x \(\frac { 2 }{ 3 } \) = 120°
and ∠B + ∠C = \(\frac { 1 }{ 2 } \) ∠A = \(\frac { 1 }{ 2 } \) x 120°
= 60°
∴ ∠ B = ∠ C
∴ ∠ B = ∠ C = \(\frac { { 60 }^{ o } }{ 2 } \) = 30°
Hence ∠ A = 120°, ∠B = 30°, ∠C = 30° Ans.
Question 5.
Solution:
In ∆ ABC,
AB = BC and ∠B = 90°
∴ AB = BC
∴ ∠ C = ∠ A
(Angles opposite to equal sides)
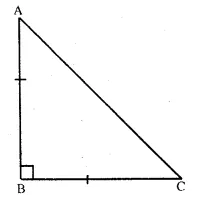
Now ∠A + ∠B + ∠C = 180°
(Sum of angles of a triangle)
=> ∠ A + 90° + ∠ A = 180°
(∴ ∠C = ∠A)
=> 2∠A + 90° – 180°
=> 2∠ A = 180° – 90° = 90°
∠ A = \(\frac { { 90 }^{ o } }{ 2 } \) = 45°
∴ ∠ C = 45° (∴ ∠ C = ∠ A)
Hence, each of the equal angles is 45° Ans.
Question 6.
Solution:
Given : ∆ ABC is an isosceles triangle in which AB = AC
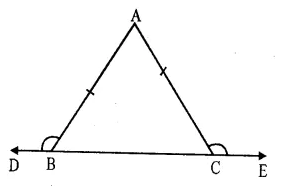
Base BC is produced to both sides upto D and E respectively forming exterior angles
∠ ABD and ∠ ACE
To Prove : ∠ABD = ∠ACE
Proof : In ∆ ABC
∴ AB = AC (given)
∴ ∠C = ∠B
(Angles opposite to equal sides)
=> ∠ ABC = ∠ACB
But ∠ ABC + ∠ABD = 180° (Linear pair)
Similarly ∠ACB + ∠ACE = 180°
∠ ABC + ∠ABD = ∠ACB + ∠ACE
But ∠ ABC = ∠ ACB (proved)
∠ABD = ∠ACE
Hence proved.
Question 7.
Solution:
∆ ABC is an equilateral triangle
∴ AB = BC = CA
and ∠A = ∠B = ∠C = 60°
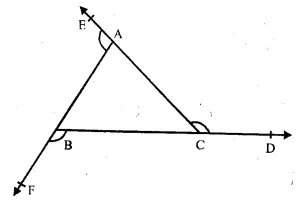
The sides of the ∆ ABC are produced in order to D,E and F forming exterior angles
∠ACP, ∠BAE and ∠CBF
∆ACD + ∠ACB = 180°
=> ∠ACD + 60° = 180°
=> ∠ACD = 180° – 60°
=> ∠ACD = 120°
Similarly, ∠BAE + ∠BAC = 180°
=> ∠BAE + 60° = 180°
=> ∠BAE = 180° – 60° = 120°
and ∠BAF + ∠ABC = 180°
=> ∠BAF + 60° = 180°
=> ∠BAF = 180° – 60° = 120°
Hence each exterior angle of an equilateral triangle is 120°.
Question 8.
Solution:
Given : In the figure,
O is mid-point of AB and CD.
i.e. OA = OB and OC = OD
To Prove : AC = BD and AC || BD.
Proof : In ∆ OAC and ∆ OBD,
OA = OB {given}
OC = OD {given}
∠AOC = ∠BOD
(Vertically opposite angles)
∴∆ OAC ≅ ∆ OBD (S.A.S. axiom)
∴AC = BD (c.p.c.t.)
and ∠ C = ∠ D
But these are alt. angles
∴AC || BD
Hence proved.
Question 9.
Solution:
Given : In the figure,
PA ⊥ AB, QB ⊥ AB and
PA = QB, PQ intersects AB at O.
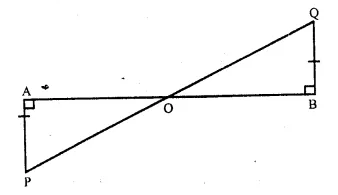
To Prove : O is mid-point of AB and PQ.
Proof : In ∆ AOP and ∆ BOQ,
∠ A = ∠ B
AP = BQ (given)
∠ AOP = ∠BOQ
(Vertically opposite angles)
∴ ∆AOP ≅ ∆ BOQ (A.A.S. axiom)
∴OA = OB (c.p.c.t)
and OP = OQ (c.p.c.t)
Hence, O is the mid-point of AB as well as PQ
Question 10.
Solution:
Given : Two line segments AB and CD intersect each other at O and OA = OB, OC = OD
AC and BD are joined.
To Prove : AC = BD
Proof : In ∆ AOC and ∆ BOD,
OA = OB {given}
OC = OD
∠AOC = ∠BOD
(vertically opposite angles)
∴ ∆ AOC ≅ ∆ BOD (S.A.S. axiom)
∴ AC = BD (c.p.c.t)
and ∠A = ∠D (c.p.c.t.)
Hence AC ≠ BD
Hence proved.
Question 11.
Solution:
Given : In the given figure,
l || m, m is mid-point of AB
CD is another line segment, which intersects AB at M.
To Prove : M is mid-point of CD
Proof : l || m
∴ ∠ CAM = ∠ MBD (Alternate angles)
Now, in ∆ AMC and ∆ BMD,
AM = MB (Given)
∠ CAM = ∠ MBD (proved)
∠ AMC = ∠BMD
(vertically opposite angles)
∆ AMC ≅ ∆ BMD (ASA axiom)
∴ CM = MD (c.p.c.t.)
Hence, M is mid-point of CD.
Similarly we can prove that M is mid point of any other line whose end points are on l and m.
Hence proved.
Question 12.
Solution:
Given : In ∆ ABC, AB = AC and in ∆ OBC,
OB = OC
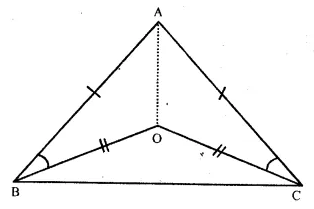
To Prove : ∠ABO = ∠ACO
Construction. Join AO.
Proof : In ∆ ABO and ∆ ACO,
AB = AC (Given)
OB = OC (Given)
AO = AO (Common)
∴ ∆ ABO ≅ ∆ ACO (S.S.S. Axiom)
∴ ∠ABO = ∠ACO (c.p.c.t.)
Hence proved.
Question 13.
Solution:
Given : In ∆ ABC, AB = AC
D is a point on AB and a line DE || AB is drawn.
Which meets AC at E
To Prove : AD = AE
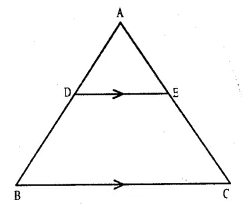
Proof : In ∆ ABC
AB = AC (given)
∴ ∠ C = ∠ B (Angles opposite to equal sides)
But DE || BC (given)
∴ ∠ D = ∠ B {corresponding angles}
and ∠ E = ∠ C
But ∠C = ∠B
∴ ∠E = ∠D
∴ AD = AE (Sides opposite to equal angles)
Hence proved.
Question 14.
Solution:
Given : In ∆ ABC,
AB = AC
X and Y are two points on AB and AC respectively such that AX = AY
To Prove : CX = BY
Proof : In ∆ AXC and ∆ AYB
AC = AB (given)
AX = AY (given)
∠ A = ∠ A (common)
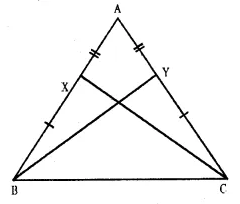
∴ ∆ AXC ≅ ∆ AYB (S.A.S. axiom)
∴ CX = BY (c.p.c.t.)
Hence proved.
Question 15.
Solution:
Given : In the figure,
C is mid point of AB
∠DCA = ∠ECB and
∠DBC = ∠EAC
To Prove : DC = EC
Proof : ∠ DCA = ∠ FCB (given)
Adding ∠ DCE both sides,
∠DCA +∠DCE = ∠DCE + ∠ECB
=> ∠ACE = ∠ BCD
Now, in ∆ ACE and ∆ BCD,
AC = BC (C is mid-point of AB)
∠EAC = ∠DBC (given)
∠ACE =∠ BCD (proved)
∴ ∆ ACE ≅ ∆ BCD (ASA axiom)
∴ CE = CD (c.p.c.t.)
=> EC = DC
or DC = EC
Hence proved.
Question 16.
Solution:
Given : In figure,
BA ⊥ AC, DE ⊥ EF .
BA = DE and BF = DC
To Prove : AC = EF
Proof : BF = DC (given)
Adding FC both sides,
BF + FC = FC + CD
=> BC = FD.
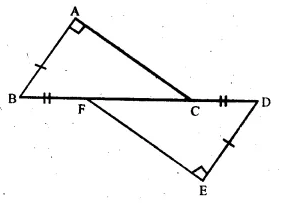
Now, in right-angled ∆ ABC and ∆ DEF,
Hyp. BC = Hyp. FD (proved)
Side AB = side DE (given)
∴ ∆ ABC ≅ ∆DEF (RHS axiom)
∴ AC = EF (c.p.c.t.)
Hence proved.
Question 17.
Solution:
To prove : AE = CD
Proof: x° + ∠ BDC = 180° (Linear pair)
Similarly y°+ ∠AEB = 180°
∴ x° + ∠BDC = y° + AEB
But x° = y° (given)
∠ BDC = ∠ AEB
Now, in ∆ AEB and ∆ BCD,
AB = CB (given)
∠B = ∠B (common)
∠ AEB = ∠ BDC (proved)
∴ ∆ AEB ≅ ∆ BCD (AAS axiom)
∴ AE = CD. (c.p.c.t.)
Hence proved.
Question 18.
Solution:
Given : In ∆ ABC,
AB = AC.
Bisectors of ∠ B and ∠ C meet AC and AB in D and E respectively
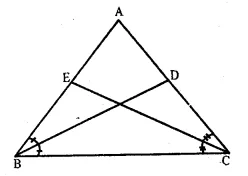
To Prove : BD = CE
Proof : In ∆ ABC,
AB = AC
∠ B = ∠ C (Angles opposite to equal sides)
Now, in ∆ ABD and ∆ ACE,
AB = AC (given)
∠ A = ∠ A (common)
∠ ABD = ∠ACE
(Half of equal angles)
∴ ∆ A ABD ≅ ∆ ACE (ASA axiom)
∴ BD = CE (c.p.c.t)
Hence proved.
Question 19.
Solution:
Given : In ∆ ABC,
AD is median. BL and CM are perpendiculars on AD and AD is produced to E
To prove : BL = CM.
Proof : In ∆ BLD and ∆ CMD,
BD = DC (D is mid-point of BC)
∠LDB = ∠CDM
(Vertically opposite angles)
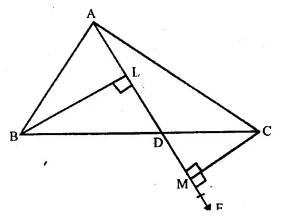
∠L = ∠M (each 90°)
∴ ∆ BLD ≅ ∆ CMD (A.A.S. axiom)
Hence, BL = CM (c.p.c.t)
Hence proved.
Question 20.
Solution:
Given : In ∆ ABC, D is mid-point of BC. DL ⊥ AB and DM ⊥ AC and DL = DM
To prove : AB = AC
Proof: In right angled ∆ BLD and ∆ CMD
Hyp. DL = DM (given)
Side BD = DC (D is mid-point of BC)
∴ ∆ BLD ≅ ∆ CMD (R.H.S. axiom)
∴ ∠B = ∠C (c.p.c.t.)
∴ AC = AB
(sides opposite to equal angles)
Hence AB = AC
Hence proved.
Question 21.
Solution:
Given : In ∆ AB = AC and bisectors of ∠B and ∠C meet at a point O. OA is joined.
To Prove : BO = CO and Ray AO is the bisector of ∠ A
Proof : AB = AC (given)
∴ ∠C = ∠B
(Angles opposite to equal sides)
=> \(\frac { 1 }{ 2 } \) ∠C = \(\frac { 1 }{ 2 } \) ∠B
=>∠OBC = ∠OCB
∴ in ∆OBC,
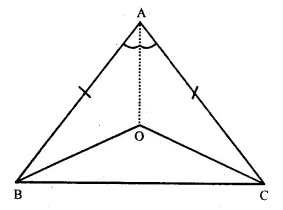
OB = OC (Sides opposite to equal angles)
Now in ∆ OAB and ∆ OCA
OB = OC (proved)
OA = OA (common)
AB = AC (given)
∴ ∆ OAB ≅ ∆ OCA (S.S.S. axiom)
∴ ∠OAB = ∠OAC (c.p.c.t.)
Hence OA is the bisector of ∠ A.
Hence proved.
Question 22.
Solution:
Given : ∆ PQR is an equilateral triangle and QRST is a square. PT and PS are joined.
To Prove : (i) PT = PS
(ii) ∠PSR = 15°
Proof : In ∆ PQT and ∆ PRS,
PQ = PR (Sides of equilateral ∆ PQR)
QT = RS (sides of in square PRST) .
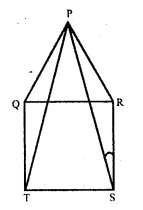
∠PQT = ∠PRS
(each angle = 90° + 60° = 150°)
∴ ∆ PQT ≅ ∆ PRS (S.A.S. axiom)
∴ PT = PS (c.p.c.t)
In ∆ PRS, ∠PRS = 60° + 90° = 150°
∠ RPS + ∠ PSR = 180° – 150° = 30°
But ∠RPS = ∠PSR ( ∴PR = RS)
∴∠PSR + ∠PSR = 30°
=> 2∠PSR = 30°
∴ ∠PSR = \(\frac { { 30 }^{ o } }{ 2 } \) = 15°
Hence proved.
Question 23.
Solution:
Given : In right angle ∆ ABC, ∠B is right angle. BCDE is square on side BC and ACFG is also a square on AC.
AD and BF are joined.
To Prove : AD = BF
Proof : ∠ACF = ∠BCD (Each 90°)
Adding ∠ ACB both sides,
∠ ACF + ∠ ACB = ∠ BCD + ∠ ACB
=> ∠ BCF = ∠ ACD
Now in ∆ ACD and ∆ BCF,
AC = CF (sides of a squares)
CD = BC (sides of a square)
∴∠ ACD = ∠ BCF (proved)
∴ ∆ ACD ≅ ∆ BCF (S.A.S. axiom)
AD = BF (c.p.c.t)
Hence proved.
Question 24.
Solution:
Given : ∆ ABC is an isosceles in which AB = AC. and AD is the median which meets BC at D.
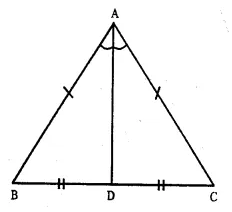
To Prove : AD is the bisector of ∠ A
Proof : In ∆ ABD and ∆ ACD,
AD = AD (Common)
AB = AC (Given)
BD = CD (D is mid-point of BC)
∴ ∆ ABD ≅ ∆ ACD (S.S.S. axiom)
∠ BAD = ∠ CAD (c.p.c.t.)
Hence, AD in the bisector of ∠ A.
Question 25.
Solution:
Given : ABCD is a quadrilateral in which AB || DC. P is mid-point of BC. AP and DC are produced to meet at Q.
To Prove : (i) AB = CQ.
(ii) DQ = DC + AB
Proof:
(i) In ∆ ABP and ∆ CPQ,
BP = PC (P is mid-point of BC)
∠ BAP = ∠ PQC (Alternate angles)
∠ APB = ∠ CPQ
(Vertically opposite angles)
∴ ∆ ABP ≅ ∆ CPQ (A.A.S. axiom)
∴ AB = CQ. (c.p.c.t.)
(ii) Now DQ = DC + CQ
=> DQ = DC + AB ( CQ = AB proved)
Hence proved.
Question 26.
Solution:
Given : In figure,
OA = OB and OP = OQ.
To Prove : (i) PX = QX (ii) AX = BX
Proof : In ∆OAQ and ∆OBP,
OA = OB. (Given)
OQ = OP (Given)
∠O = ∠O (Common)
∴ ∆ OAQ ≅ ∆ OBP (SAS axiom)
∴ ∠ A = ∠ B (c.p.c.t)
Now OA = OB and OP = OQ
Subtracting
OA – OP = OB – OQ
=>PA = QB
Now, in ∆ XPA and ∆ XQB,
PA = QB (Proved)
∠AXP = ∠BXQ
(Vertically opposite angles)
∠ A = ∠ B (Proved)
∴ ∆ XPA ≅ ∆ XQB (A.A.S. axiom)
∴ AX = BX (c.p.c.t.) and PX = QX (c.p.c.t.)
Hence proved.
Question 27.
Solution:
Given : ABCD is a square in which a point P is inside it. Such that PB = PD.
To prove : CPA is a straight line.
Proof : In ∆ APB and ∆ ADP,
AB = AD (Sides of a square)
AP = AP (Common)
PB = PD (Given)
∴ ∆ APB ≅ ∆ ADP (S.S.S. axiom)
∠APD = ∠ APB (c.p.c.t) …(i)
Similarly, in ∆ CBP and ∆ CPD,
CB = CD (Sides of a square)
CP – CP (Common)
PB = PD (Given)
∴ ∆ CBP ≅ ∆ CPD (S.S.S. axiom)
∴ ∠BPC = ∠CPD (c.p.c.t.) …(i)
Adding (i) and (ii),
∴ ∠ APD + ∠ CPD = ∠ APB + ∠ BPC
∠APC = ∠APC
∠APC = 180°
(v sum of angles at a point is 360°)
APC or CPA is a straight line.
Hence proved.
Question 28.
Solution:
Given :∆ ABC is an equilateral triangle PQ || AC and AC is produced to R such that CR = BP
To prove : QR bisects PC
Proof : ∴ PQ || AC
∴ ∠BPQ = ∠BCA
(Corresponding angles)
But ∠ BCA = 60°
(Each angle of the equilateral triangle)
and ∠ ABC or ∠QBP = 60°
∴ ∆ BPQ is also an equilateral triangle.
∴ BP = PQ
But BP = CR (Given)
∴ PQ = CR
Now in ∆ PQM and ∆ RMC,
PQ = CR (proved)
∠QMP = ∠RMC
(vertically opposite angles)
∠ PQM = ∠ MRC (alternate angles)
∴ ∆ PQM ≅ ∆ RMC (AAS axiom)
∴ PM = MC (c.p.c.t.)
Hence, QR bisects PC.
Hence proved
Question 29.
Solution:
Given : In quadrilateral ABCD,
AB = AD and BC = DC
AC and BD are joined.
To prove : (i) AC bisects ∠ A and ∠ C
(ii) AC is perpendicular bisector of BD.
Proof : In ∆ ABC and ∆ ADC,
AB = AD (given)
BC = DC (given)
AC = AC (common)
∴ ∆ ABC ≅ ∆ ADC (S.S.S. axiom)
∴ ∠BCA = ∠DCA (c.p.c.t.)
and ∠BCA = ∠DAC (c.p.c.t.)
Hence AC bisects ∠ A and ∠ C
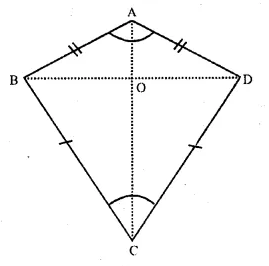
(ii) In ∆ ABO and ∆ ADO,
AB = AD (given)
AO = AO (common)
∠BAO = ∠DAO
(proved that AC bisects ∠ A)
∴ ∆ ABO ≅ ∆ ADO (SAS axiom)
∴ BO = OD and ∠AOB = ∠AOD (c.p.c.t.)
But ∠ AOB + ∠ AOD = 180° (linear pair)
∠AOB = ∠AOD = 90°
Hence AC is perpendicular bisector of BD. Hence proved.
Question 30.
Solution:
Given : In ∆ ABC,
Bisectors of ∠ B and ∠ C meet at I
From I, IP ⊥ BC. IQ ⊥ AC and IR ⊥ AB.
IA is joined.
To prove : (i) IP = IQ = IR
(ii) IA bisects ∠ A.
Proof : (i) In ∆ BIP and ∆ BIR
BI = BI (Common)
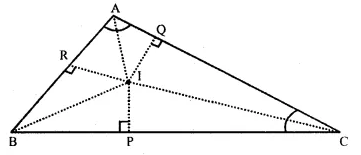
and ∠P = ∠R (Each 90°)
∴ ∠ IBP ≅ ∠ IBR
( ∴ IB is bisector of ∠ B)
∴ ∆ BIP = ∆ BIR (A.A.S. axiom)
∴ IP = IR (c.p.c.t) …(i)
Similarly, in ∆ CIP and ∆ CIQ,
CI = CI (Common)
∠P = ∠Q (each = 90°) and ∠ICP = ∠ ICR
( IC is bisector of ∠ C)
∴ ∆CIP ≅ ∆CIQ (A.A.S. axiom)
∴ IP = IQ (c.p.c.t.) …(ii)
From (i) and (ii),
IP = IQ = IR.
(i) In right angled ∆ IRA and ∆ IQA,
Hyp. IA = IA (Common)
side IR = IQ (Proved)
∴ ∆ IRA ≅ ∆ IQA (R.H.S. axiom)
∴ ∠IAR = ∠ IRQ (c.p.c.t.)
Hence IA is the bisector of ∠ A
Hence proved.
Question 31.
Solution:
Given. P is a point in the interior of ∠ AOB
PL ⊥ OA and PM ⊥ OC are drawn and PL = PM.
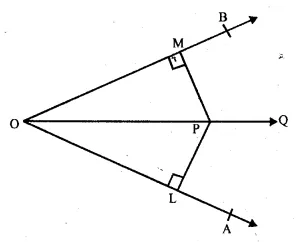
To prove : OP is the bisector of ∠ AOB
Proof: In right angled ∆ OPL and ∆ OPM,
Hyp. OP OP (Common)
Side PL = PM (Given)
∴ ∆ OPL ≅ ∆ OPM (R.H.S. axiom)
∴ ∠POL = ∠POM (c.p.c.t.)
Hence, OP is the bisector of ∠AOB.
[ Hence proved.
Question 32.
Solution:
Given : ABCD is a square, M is midpoint of AB.
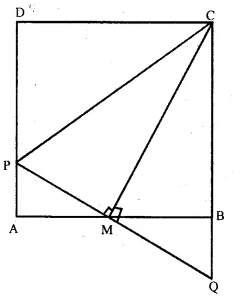
PQ is perpendicular to MC which meets CB produced at Q. CP is joined.
To prove : (i) PA = BQ
(ii) CP = AB + PA
Proof : (i) In ∆ PAM and ∆ QBM,
AM = MB (M is midpoint of AB)
∠AMP = ∠BMQ
(vertically opposite angles)
∠ PAM = ∠ QBM
(Each = 90° angles of a square)
∴ ∆ PAM ≅ ∆ QBM (A.S.A. axiom)
∴ AP = BQ
=> PA = BQ (c.p.c.t.)
and PM = QM (c.p.c.t.)
Now, in ∆ CPM and ∆ CQM,
CM = CM (Common)
PM = QM (Proved)
∠CMP =∠CMQ (Each 90° as PQ ⊥ MC)
∴ ∆ CPM ≅ ∆ CQM (SAS axiom)
∴ CP = CQ (c.p.c.t.)
= CB + BQ
= AB + PA
( CB = AB sides of squares and BQ = PA proved)
Hence, CP = AB + PA.
Question 33.
Solution:
Construction. Let AB be the breadth of the river. Mark any point M on the bank on which B is situated. Let O be the midpoint of BM. From M move along the path MN perpendicular to BM to a point N such that A, O, N are on the same straight line. Then MN is the required breadth of the river.
Proof : In ∆ ABO and ∆ MNO,
BO = OM (const.)
∠ AOB = ∠ MON (vertically opposite angle)
∠B = ∠M (each 90°)
∴ ∆ ABO ≅ ∆ MNO (A.S.A. axiom)
∴ AB = MN. (c.p.c.t.)
Hence, MN is the required breadth of the river.
Question 34.
Solution:
In ∆ ABC,
∠A = 36°, ∠B = 64°
But ∠A + ∠B + ∠C = 180°
(Sum of angles of a triangle)
=> 36° + 64° + ∠C = 180°
=> 100° + ∠C = 180°
=> ∠C = 180° – 100° = 80°
∴ ∠ C = 80° which is the greatest angle.
∴ The side AB, opposite to it is the longest side.
∴∠ A is the shortest angle
∴ BC is the shortest side.
Question 35.
Solution:
In ∆ ABC,
∴ ∠A = 90°
∴ ∠B + ∠C 180° – 90° = 90°
Hence, ∠ A is the greatest angle of the triangle.
Side BC, opposite to this angle be the longest side.
Question 36.
Solution:
In ∆ ABC,
∠ A = ∠ B = 45°
∴ ∠A + ∠B = 45° + 45° = 90°
and ∠C= 180°-90° = 90°
∴ ∠ C is the greatest angle.
∴ Side AB, opposite to ∠ C will be the longest side of the triangle.
Question 37.
Solution:
Given : In ∆ ABC, side AB is produced to D such that BD = BC.
∠B = 60°, ∠A = 70°
To Prove : (i) AD > CD (ii) AD > AC
Proof : In ∆ BCD,
Ext. ∠ B = 60°
∴ ∠ CBD = 180° – 60° = 120°
and ∠ BCD + ∠ BDC = Ext. ∠ CBA = 60°
But ∠BCD = ∠ BDC ( BC = BD)
∴ ∠BCD = ∠BDC = \(\frac { { 60 }^{ o } }{ 2 } \) = 30°.
∴ ∠ ACD = 50° + 30° = 80°
(i) Now in ∆ ACD,
∴ ∠ ACD > ∠ CAD ( 80° > 70°)
AD > CD .
(ii) and ACD > ∠D (80° > 30°)
∴ AD > AC
Hence proved.
Question 38.
Solution:
Given : In ∆ ABC, ∠B = 35°and ∠C = 65°
AX is the bisector of ∠ BA C meeting BC in X
∠A + ∠B + ∠C = 180°
(Sum of angles of a triangle)
=> ∠ A + 35° + 65° = 180°
=> ∠A + 100° = 180°
=> ∠A = 180° – 100° = 80°
∴ AX is the bisector of ∠ BAC
∴ ∠ BAX = ∠ CAX = 40°
In ∆ ABX,
∠BAX = 40° and ∠B = 35°
∴ ∠BAX > ∠B
∴ BX > AX …(i)
and in ∆ AXC,
∠C = 65° and ∠CAX = 40°
∴ ∠C > ∠CAX
∴ AX > XC …(ii)
From (i) and (ii),
BX > AX > XC
or BX > AX > CX
Question 39.
Solution:
Given : In ∆ ABC,
AD is the bisector of ∠ A
To prove : (i) AB > BD and
(ii) AC > DC
Proof : (i) In ∆ ADC,
Ext. ∠ ADB > ∠ CAD
=>∠ ADB > ∠BAD ,
( AD is bisector of ∠ A)
In ∆ ABD,
AB > BD.
(ii) Again, in ∆ ADB,
Ext. ∠ADC > ∠BAD
=> ∠ADC > ∠CAD
( ∠ CAD = ∠BAD)
Now in ∆ ACD.
AC > DC.
Hence proved
Question 40.
Solution:
Given : In ∆ ABC, AB = AC
BC is produced to D and AD is joined.
To Prove : AD > AC
Proof : In ∆ ABC,
AB = AC (given)
∴ ∠B = ∠C (Angles opposite to equal sides)
Ext. ∠ ACD > ∠ ABC
∠ACB = ∠ABC
∴ ∠ABC > ∠ADC
Now, in ∆ ABD,
∴ ∠ABC > ∠ADC or ∠ADB
∴ AD > AC
Hence proved.
Question 41.
Solution:
Given : In ∆ ABC,
AC > AB and AD is the bisector of ∠ A which meets BC in D.
To Prove : ∠ADC > ∠ADB
Proof : In ∆ ABC,
AC > AB
∴∠B > ∠C
∴∠ 1 = ∠ 2 (AD is the bisector of ∠ A)
∴ ∠B + ∠2 = ∠C + ∠1
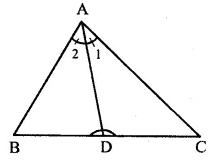
But in ∆ ADB
Ext. ∠ADC = ∠B + ∠2
and in ∆ ADC,
Ext. ∠ADB > ∠C + ∠1
∴ ∠B + ∠2 > ∠C + ∠1 (Proved)
∴ ∠ ADC > ∠ ADB Hence proved.
Question 42.
Solution:
Given : In ∆ PQR,
S is any point on QR and PS is joined
To Prove : PQ + QR + RP > 2PS
Proof : In ∆ PQS,
PQ + QS > PS
(Sum of two sides of a triangle is greater than the third side) …(i)
Similarly, in ∆ PRS.
PQ + SR > PS …(ii)
Adding (i), and (ii),
PQ + QS + PR + SR > PS + PS
=> PQ + QS + SR + PR > 2PS
=> PQ + QR + RP > 2PS
Hence proved.
Question 43.
Solution:
Given : O is the centre of the circle and XOY is its diameter.
XZ is the chord of this circle
To Prove : XY > XZ
Const. Join OZ
Proof : OX, OZ and OY are the radii of the circle
∴ OX = OZ = OY
In ∆ XOZ,
OX + OZ > XZ (Sum of two sides of a triangle is greater than its third side)
=> OX + OY > XZ (∴ OZ = OY)
=> OXY > XZ
Hence proved.
Question 44.
Solution:
Given : In ∆ ABC, O is any point within it OA, OB and OC are joined.
To Prove : (i) AB + AC > OB + OC
(ii) AB + BC + CA > OA + OB + OC
(iii) OA + OB + OC > \(\frac { 1 }{ 2 } \)
(AB + BC + CA)
Const. Produce BO to meet AC in D.
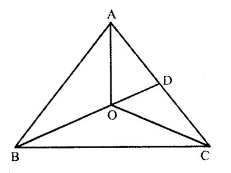
Proof : (i) In ∆ ABD,
AB + AD > BD …(i)
(Sum of two sides of a triangle is greater than its third side)
=> AB + AD > BO + OD …(i)
Similarly in ∆ ODC
OD + DC > OC. …(ii)
Adding (i) and (ii)
AB + AD + OD + DC > OB + OD + OC
=> AB + AD + DC > OB + OC
AB + AC > OB + OC.
(ii) In (i) we have proved that
AB + AC > OB + OC
Similarly, we can prove that
AC + BC > OC + OA
and BC + AB > OA + OB
Adding, we get:
AB + AC + AC + BC + B + AB > OB + OC + OC + OA + OA + OB
=> 2(AB + BC + CA) > 2(OA + OB + OC)
=> AB + BC + CA > OA + OB + OC.
(iii) In ∆ AOB,
OA + OB > AB
Similarly, in ∆ BOC
OB + OC > BC
and in ∆ COA
OC + OA > CA
adding we get:
OA + OB + OB + OC + OC + OA > AB + BC + CA
=> 2(OA + OB + OC) > (AB + BC + CA)
=> OA + OB + OC > \(\frac { 1 }{ 2 } \) (AB + BC + CA)
Hence proved.
Question 45.
Solution:
Sides of ∆ ABC are AB = 3cm, BC = 3.5cm and CA = 6.5cm
We know that sum of any two sides of a triangle is greater than its third side.
Here, AB = 3 cm and BC = 3.5 cm
∴ AB + BC = 3cm + 3.5 cm = 6.5 cm and CA = 6.5 cm
∴ AB + BC = CA
Which is not possible to draw the triangle.
Hence, we cannot draw the triangle with the given data.
Hope given RS Aggarwal Class 9 Solutions Chapter 5 Congruence of Triangles and Inequalities in a Triangle Ex 5A are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.