RD Sharma Class 9 Solutions Chapter 4 Algebraic Identities Ex 4.5
These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 4 Algebraic Identities Ex 4.5
Question 1.
Find the following products:
(i) (3x + 2y + 2z) (9x2 + 4y2 + 4z2 – 6xy – 4yz – 6zx)
(ii) (4x -3y + 2z) (16x2 + 9y2+ 4z2 + 12xy + 6yz – 8zx)
(iii) (2a – 3b – 2c) (4a2 + 9b2 + 4c2 + 6ab – 6bc + 4ca)
(iv) (3x -4y + 5z) (9x2 + 16y2 + 25z2 + 12xy- 15zx + 20yz)
Solution:
(i) (3x + 2y + 2z) (9x2 + 4y2 + 4z2 – 6xy – 4yz – 6zx)
= (3x + 2y + 2z) [(3x)2 + (2y)2 + (2z)2 – 3x x 2y + 2y x 2z + 2z x 3x]
= (3x)3 + (2y)3 + (2z)3 – 3 x 3x x 2y x 2z
= 27x3 + 8y3 + 8Z3 – 36xyz
(ii) (4x – 3y + 2z) (16x2 + 9y2 + 4z2 + 12xy + 6yz – 8zx)
= (4x -3y + 2z) [(4x)2 + (-3y)2 + (2z)2 – 4x x (-3y + (3y) x (2z) – (2z x 4x)]
= (4x)3 + (-3y)3 + (2z)3 – 3 x 4x x (-3y) x (2z)
= 64x3 – 27y3 + 8z3 + 72xyz
(iii) (2a -3b- 2c) (4a2 + 9b2 + 4c2 + 6ab – 6bc + 4ca)
= (2a -3b- 2c) [(2a)2 + (3b)2 + (2c)2 – 2a x (-3b) – (-3b) x (-2c) – (-2c) x 2a]
= (2a)3 + (3b)3 + (-2c)3 -3x 2a x (-3 b) (-2c)
= 8a3 – 21b3 -8c3 – 36abc
(iv) (3x – 4y + 5z) (9x2 + 16y2 + 25z2 + 12xy – 15zx + 20yz)
= [3x + (-4y) + 5z] [(3x)2 + (-4y)2 + (5z)2 – 3x x (-4y) -(-4y) (5z) – 5z x 3x]
= (3x)3 + (-4y)3 + (5z)3 – 3 x 3x x (-4y) (5z)
= 27x3 – 64y3 + 125z3 + 180xyz
Question 2.
Evaluate:
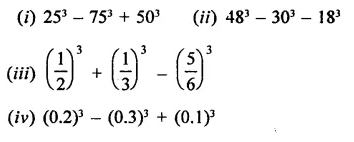
Solution:
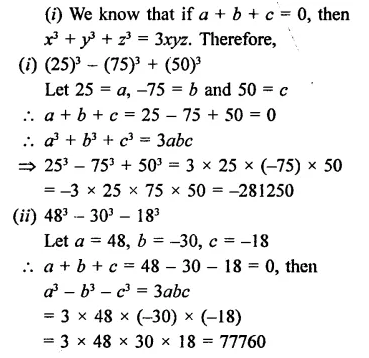
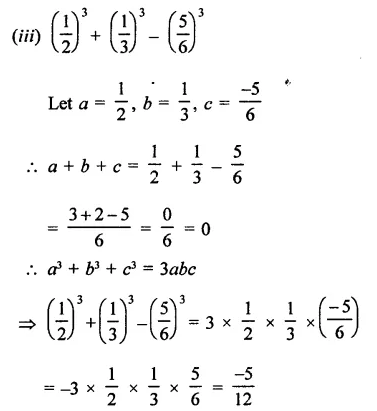
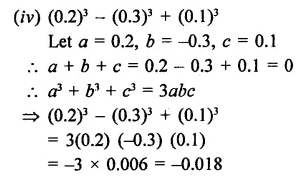
Question 3.
If x + y + z = 8 and xy + yz+ zx = 20, find the value of x3 + y3 + z3 – 3xyz.
Solution:
We know that
x3 + y3 + z3 – 3xyz = (x + y + z) (x2 + y2 + z2 -xy -yz – zx)
Now, x + y + z = 8
Squaring, we get
(x + y + z)2 = (8)2
x2 + y2 + z2 + 2(xy + yz + zx) = 64
⇒ x2 + y2 + z2 + 2 x 20 = 64
⇒ x2 + y2 + z2 + 40 = 64
⇒ x2 + y2 + z2 = 64 – 40 = 24
Now,
x3 + y3 + z3 – 3xyz = (x + y + z) [x2 + y2 + z2 – (xy + yz + zx)]
= 8(24 – 20) = 8 x 4 = 32
Question 4.
If a +b + c = 9 and ab + bc + ca = 26, find the value of a3 + b3 + c3 – 3abc.
Solution:
a + b + c = 9, ab + be + ca = 26
Squaring, we get
(a + b + c)2 = (9)2
a2 + b2 + c2 + 2 (ab + be + ca) = 81
⇒ a2 + b2 + c2 + 2 x 26 = 81
⇒ a2 + b2 + c2 + 52 = 81
∴ a2 + b2 + c2 = 81 – 52 = 29
Now, a3 + b3 + c3 – 3abc = (a + b + c) [(a2 + b2 + c2 – (ab + bc + ca)]
= 9[29 – 26]
= 9 x 3 = 27
Question 5.
If a + b + c = 9, and a2 + b2 + c2 = 35, find the value of a3 + b3 + c3 – 3abc.
Solution:
a + b + c = 9
Squaring, we get
(a + b + c)2 = (9)2
⇒ a2 + b2 + c2 + 2 (ab + be + ca) = 81
⇒ 35 + 2(ab + bc + ca) = 81
2(ab + bc + ca) = 81 – 35 = 46
∴ ab + bc + ca = \(\frac { 46 }{ 2 }\) = 23
Now, a3 + b3 + c3 – 3abc
= (a + b + c) [a2 + b2 + c2 – (ab + bc + ca)]
= 9[35 – 23] = 9 x 12 = 108
Hope given RD Sharma Class 9 Solutions Chapter 4 Algebraic Identities Ex 4.5 are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.