RD Sharma Class 9 Solutions Chapter 11 Co-ordinate Geometry VSAQS
These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 11 Co-ordinate Geometry VSAQS
Other Exercises
- RD Sharma Class 9 Solutions Chapter 11 Co-ordinate Geometry Ex 11.1
- RD Sharma Class 9 Solutions Chapter 11 Co-ordinate Geometry Ex 11.2
- RD Sharma Class 9 Solutions Chapter 11 Co-ordinate Geometry VSAQS
- RD Sharma Class 9 Solutions Chapter 11 Co-ordinate Geometry MCQS
Question 1.
Define a triangle.
Solution:
A figure bounded by three lines segments in a plane is called a triangle.
Question 2.
Write the sum of the angles of an obtuse triangle.
Solution:
The sum of angles of an obtuse triangle is 180°.
Question 3.
In ∆ABC, if ∠B = 60°, ∠C = 80° and the bisectors of angles ∠ABC and ∠ACB meet at a point O, then find the measure of ∠BOC.
Solution:
In ∆ABC, ∠B = 60°, ∠C = 80°
OB and OC are the bisectors of ∠B and ∠C
∵ ∠A + ∠B + ∠C = 180° (Sum of angles of a triangle)
⇒ ∠A + 60° + 80° = 180°
⇒ ∠A + 140° = 180°
∴ ∠A = 180°- 140° = 40°
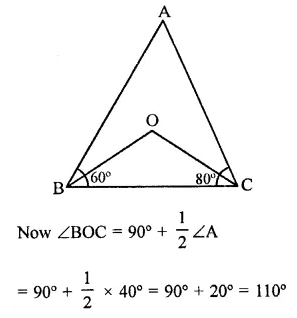
= 90° + – x 40° = 90° + 20° = 110°
Question 4.
If the angles of a triangle are in the ratio 2:1:3. Then find the measure of smallest angle.
Solution:
Sum of angles of a triangle = 180°
Ratio in the angles = 2 : 1 : 3
Let first angle = 2x
Second angle = x
and third angle = 3x
∴ 2x + x + 3x = 180° ⇒ 6x = 180°
∴ x = \(\frac { { 180 }^{ \circ } }{ 6 }\) = 30°
∴ First angle = 2x = 2 x 30° = 60°
Second angle = x = 30°
and third angle = 3x = 3 x 30° = 90°
Hence angles are 60°, 30°, 90°
Question 5.
State exterior angle theorem.
Solution:
Given : In ∆ABC, side BC is produced to D
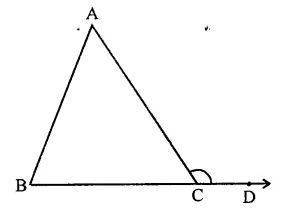
To prove : ∠ACD = ∠A + ∠B
Proof: In ∆ABC,
∠A + ∠B + ∠ACB = 180° …(i) (Sum of angles of a triangle)
and ∠ACD + ∠ACB = 180° …(ii) (Linear pair)
From (i) and (ii)
∠ACD + ∠ACB = ∠A + ∠B + ∠ACB
∠ACD = ∠A + ∠B
Hence proved.
Question 6.
The sum of two angles of a triangle is equal to its third angle. Determine the measure of the third angle.
Solution:
In ∆ABC,
∠A + ∠C = ∠B
But ∠A + ∠B + ∠C = 180° (Sum of angles of a triangle)
∴ ∠B + ∠A + ∠C = 180°
⇒ ∠B + ∠B = 180°
⇒ 2∠B = 180°
⇒ ∠B = \(\frac { { 180 }^{ \circ } }{ 2 }\) = 90°
∴ Third angle = 90°
Question 7.
In the figure, if AB || CD, EF || BC, ∠BAC = 65° and ∠DHF = 35°, find ∠AGH.
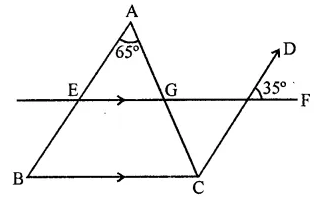
Solution:
Given : In figure, AB || CD, EF || BC ∠BAC = 65°, ∠DHF = 35°
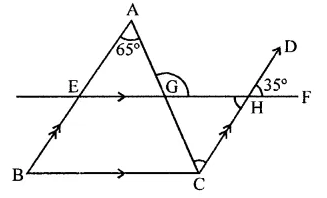
∵ EF || BC
∴ ∠A = ∠ACH (Alternate angle)
∴ ∠ACH = 65°
∵∠GHC = ∠DHF
(Vertically opposite angles)
∴ ∠GHC = 35°
Now in ∆GCH,
Ext. ∠AGH = ∠GCH + ∠GHC
= 65° + 35° = 100°
Question 8.
In the figure, if AB || DE and BD || FG such that ∠FGH = 125° and ∠B = 55°, find x and y.
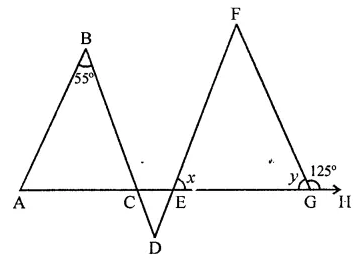
Solution:
In the figure, AB || DF, BD || FG
∠FGH = 125° and ∠B = 55°
∠FGH + FGE = 180° (Linear pair)
⇒ 125° + y – 180°
⇒ y= 180°- 125° = 55°
∵ BA || FD and BD || FG
∠B = ∠F = 55°
Now in ∆EFG,
∠F + ∠FEG + ∠FGE = 180°
(Angles of a triangle)
⇒ 55° + x + 55° = 180°
⇒ x+ 110°= 180°
∴ x= 180°- 110° = 70°
Hence x = 70, y = 55°
Question 9.
If the angles A, B and C of ∆ABC satisfy the relation B – A = C – B, then find the measure of ∠B.
Solution:
In ∆ABC,
∠A + ∠B + ∠C= 180° …(i)
and B – A = C – B
⇒ B + B = A + C ⇒ 2B = A + C
From (i),
B + 2B = 180° ⇒ 3B = 180°
∠B = \(\frac { { 180 }^{ \circ } }{ 3 }\) = 60°
Hence ∠B = 60°
Question 10.
In ∆ABC, if bisectors of ∠ABC and ∠ACB intersect at O at angle of 120°, then find the measure of ∠A.
Solution:
In ∆ABC, bisectors of ∠B and ∠C intersect at O and ∠BOC = 120°
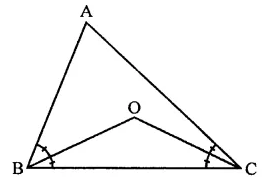
But ∠BOC = 90°+ \(\frac { 1 }{ 2 }\)
90°+ \(\frac { 1 }{ 2 }\) ∠A= 120°
⇒ \(\frac { 1 }{ 2 }\) ∠A= 120°-90° = 30°
∴ ∠A = 2 x 30° = 60°
Question 11.
If the side BC of ∆ABC is produced on both sides, then write the difference between the sum of the exterior angles so formed and ∠A.
Solution:
In ∆ABC, side BC is produced on both sides forming exterior ∠ABE and ∠ACD
Ext. ∠ABE = ∠A + ∠ACB
and Ext. ∠ACD = ∠ABC + ∠A
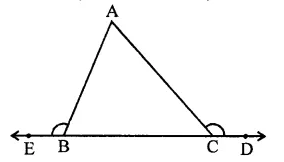
Adding we get,
∠ABE + ∠ACD = ∠A + ∠ACB + ∠A + ∠ABC
⇒ ∠ABE + ∠ACD – ∠A = ∠A 4- ∠ACB + ∠A + ∠ABC – ∠A (Subtracting ∠A from both sides)
= ∠A + ∠ABC + ∠ACB = ∠A + ∠B + ∠C = 180° (Sum of angles of a triangle)
Question 12.
In a triangle ABC, if AB = AC and AB is produced to D such that BD = BC, find ∠ACD: ∠ADC.
Solution:
In ∆ABC, AB = AC
AB is produced to D such that BD = BC
DC are joined
In ∆ABC, AB = AC
∴ ∠ABC = ∠ACB
In ∆ BCD, BD = BC
∴ ∠BDC = ∠BCD
and Ext. ∠ABC = ∠BDC + ∠BCD = 2∠BDC (∵ ∠BDC = ∠BCD)
⇒ ∠ACB = 2∠BCD (∵ ∠ABC = ∠ACB)
Adding ∠BDC to both sides
⇒ ∠ACB + ∠BDC = 2∠BDC + ∠BDC
⇒ ∠ACB + ∠BCD = 3 ∠BDC (∵ ∠BDC = ∠BCD)
⇒ ∠ACB = 3∠BDC
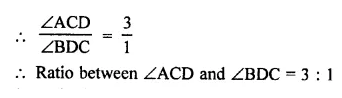
Question 13.
In the figure, side BC of AABC is produced to point D such that bisectors of ∠ABC and ∠ACD meet at a point E. If ∠BAC = 68°, find ∠BEC.
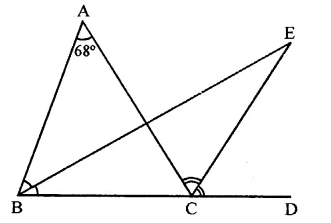
Solution:
In the figure,
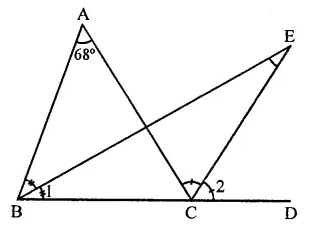
side BC of ∆ABC is produced to D such that bisectors of ∠ABC and ∠ACD meet at E
∠BAC = 68°
In ∆ABC,
Ext. ∠ACD = ∠A + ∠B
⇒ \(\frac { 1 }{ 2 }\) ∠ACD = \(\frac { 1 }{ 2 }\) ∠A + \(\frac { 1 }{ 2 }\) ∠B
⇒ ∠2= \(\frac { 1 }{ 2 }\) ∠A + ∠1 …(i)
But in ∆BCE,
Ext. ∠2 = ∠E + ∠l
⇒ ∠E + ∠l = ∠2 = \(\frac { 1 }{ 2 }\) ∠A + ∠l [From (i)]
⇒ ∠E = \(\frac { 1 }{ 2 }\) ∠A = \(\frac { { 68 }^{ \circ } }{ 2 }\) =34°
Hope given RD Sharma Class 9 Solutions Chapter 11 Co-ordinate Geometry VSAQS are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.