NCERT Solutions for Class 8 Maths Chapter 3 Understanding Quadrilaterals Ex 3.3 are part of NCERT Solutions for Class 8 Maths. Here we have given NCERT Solutions for Class 8 Maths Chapter 3 Understanding Quadrilaterals Ex 3.3.
- Understanding Quadrilaterals Class 8 Ex 3.1
- Understanding Quadrilaterals Class 8 Ex 3.2
- Understanding Quadrilaterals Class 8 Ex 3.4
| Board | CBSE |
| Textbook | NCERT |
| Class | Class 8 |
| Subject | Maths |
| Chapter | Chapter 3 |
| Chapter Name | Understanding Quadrilaterals |
| Exercise | Ex 3.3 |
| Number of Questions Solved | 12 |
| Category | NCERT Solutions |
NCERT Solutions for Class 8 Maths Chapter 3 Understanding Quadrilaterals Ex 3.3
Question 1.
Given a parallelogram ABCD. Complete each statement along with the definition with the definition or property used.
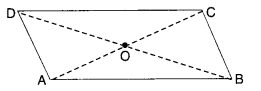
(i) AD = ………
(ii) ∠DCB = …………….
(iii) OC = ……………….
(iv) m∠DAB + m∠CDA = …………..
Solution.
(i) AD = BC
Opposite sides of a parallelogram are equal
(ii) ∠DCB = ∠DAB
Opposite angles of a parallelogram are equal
(iii) OC = OA
∵ Diagonals of a parallelogram bisect each other
(iv) m∠DAB + m∠CDA = 180°
∵ Adjacent angles of a parallelogram are supplementary.
Question 2.
Consider the following parallelo¬grams. Find the values of the unknowns x, y, z.
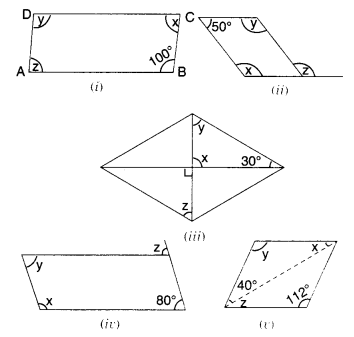
Solution.
(i) y = 100°
Opposite angles of a parallelogram are equal
x + 100° = 180°
Adjacent angles in a parallelogram are supplementary
⇒ x = 180° – 100°
⇒ x = 80°
⇒ z – x = 80°
Opposite angles of a parallelogram are of equal measure
(ii) x + 50° = 180°
Adjacent angles in a parallelogram are supplementary
⇒ x = 180° – 50° = 130°
⇒ y = x = 130°
The opposite angles of a parallelogram are of equal measure
180° – z = 50°
Opposite angles of a parallelogram are of equal measure
⇒ z = 180° – 50° = 130°
(iii) x = 90°
Vertically opposite angles are equal
x + y + 30° = 180°
By angle sum property of a triangle
⇒ 90° + y + 30° = 180°
⇒ 120° + y = 180°
⇒ y = 180° – 120° = 60° z + 30° + 90° – 180°
By angle sum property of a triangle
z = 60°
(iv) y = 80°
Opposite angles of a parallelogram are of equal measure
x + 80° = 180°
Adjacent angles in a parallelogram are supplementary
⇒ x = 180° – 80°
⇒ x = 100°
⇒ 180°-2+ 80°= 180°
Linear pair property and adjacent angles in a parallelogram are supplementary.
z = 80°
(v) y = 112°
Opposite angles of a parallelogram are equal
x + y + 40° = 180°
By angle sum property of a triangle
⇒ x + 112° + 40° = 180°
⇒ x + 152° = 180°
⇒ x = 180°- 152°
⇒ x = 28°
z = x = 28°.
Alternate interior angles
Question 3.
Can a quadrilateral ABCD be a parallelogram if
(i) ∠D + ∠B = 180° ?
(ii) AB = DC = 8 cm, AD = 4 cm and BC = 4.4 cm
(iii) ∠A = 70° and ∠C = 65°?
Solution.
(i) Can be, but need not be
(ii) No: in a parallelogram, opposite sides are equal; but here, AD ≠ BC.
(iii) No: in a parallelogram, opposite angles are of equal measure; but here ∠A ≠ ∠C.
Question 4.
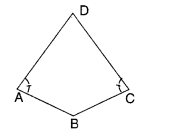
Draw a rough figure of a quadrilateral that is not a parallelogram but has exactly two opposite angles of equal measure.
Solution.
A kite, for example
Question 5.
The measures of two adjacent angles of a parallelogram are in the ratio 3:2. Find the measure of each of the angles of the parallelogram.
Solution.
Let the two adjacent angles be 3x° and 2x°.
Then,
3x° + 2x° = 180°
∴ Sum of the two adjacent angles of a parallelogram is 180°
⇒ 5x° = 180°
⇒ \({ x }^{ \circ }=\frac { { 180 }^{ \circ } }{ 5 } \)
⇒ x° = 36°
⇒ 3x° = 3 x 36° = 108°
and
2x° = 2 x 36° = 72°.
Since, the opposite angles of a parallelogram are of equal measure, therefore the measures of the angles of the parallelogram are 72°, 108°, 72°, and 108°.
Question 6.
Two adjacent angles of a parallelogram have equal measure. Find the measure of each of the angles of the parallelogram.
Solution.
Let the two adjacent angles of a parallelogram be x° each.
Then,
x° + x° = 180°
∴ Sum of the two adjacent angles of a parallelogram is 180°.
⇒ 2x° = 180°
⇒ \({ x }^{ \circ }=\frac { { 180 }^{ \circ } }{ 2 } \)
⇒ x° = 90°.
Since the opposite angles of a parallelogram are of equal measure, therefore the measure of each of the angles of the parallelogram is 90°, i.e., each angle of the parallelogram is a right angle.
Question 7.
The adjacent figure HOPE is a parallelogram. Find the angle measures x, y and z. State the properties you use to find them.
Solution.
x = 180° – 70° = 110°
Linear pair property and the opposite angles of a parallelogram are of equal measure.
∵ HOPE is a || gm
∴ HE || OP
and HP is a transversal
∴ y = 40°
alternate interior angles
40° + z + x = 180°
The adjacent angles in a parallelogram are supplementary
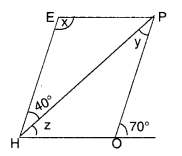
⇒ 40° + z + 110° = 180°
⇒ z + 150° = 180°
⇒ z = 180° – 150°
⇒ z = 30°.
Question 8.
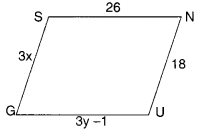
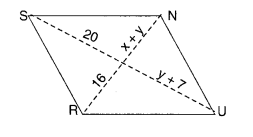
The following figures GUNS and RUNS are parallelograms. Find x and y. (Lengths are in cm)
(i)
(ii)
Solution.
(i)
For Figure GUNS
Since the opposite sides of a parallelogram are of equal length, therefore,
⇒ 3x = 18
⇒ \(x=\frac { 18 }{ 3 } =6\)
and, 3y – 1 = 26
⇒ 3y = 26 + 1
⇒ 3y = 27
\(y=\frac { 27 }{ 3 } =9\)
Hence, x = 6; y = 9.
(ii)
For Figure RUNS
Since the diagonals of a parallelogram bisect each other, therefore,
⇒ x + y = 16 …(1)
and, y + 7 = 20 …(2)
From (2),
⇒ y – 20 – 7 = 13
Putting y = 13 in (1), we get
⇒ x + 13 = 16 ⇒ x = 16 – 13 = 3.
Hence, x = 3; y = 13.
Question 9.
In the below figure both RISK and CLUE are parallelograms. Find the value of x.
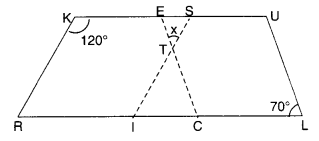
Solution.


Question 10.
Explain how this figure is a trapezium. Which of its two sides is parallel?
Solution.

∵ ∠KLM + ∠NML = 80° + 100° = 180°
∴ KL || NM
∵ The sum of consecutive interior angles is 180°
∴ Figure KLMN is a trapezium.
Its two sides \(\overline { KL } \) and \(\overline { NM } \) are parallel.
Question 11.
Find m∠C in the figure, if \(\overline { AB } \) || \(\overline { DC } \).
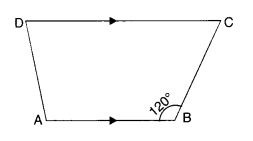
Solution.
∵ \(\overline { AB } \) || \(\overline { DC } \)
∴ m∠C + m∠B = 180°
∵ The sum of consecutive interior angles is 180°
m∠C+ 120° = 180°
⇒ m∠C = 180° – 120° = 60°.
Question 12.
Find the measure of ∠P and ∠S, if \(\overline { SP } \) || \(\overline { RQ } \) in the figure. (If you find mZ R, is there more than one method to find m∠P ?)
Solution.
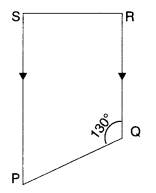
∵ \(\overline { SP } \) || \(\overline { RQ } \)
∴ m∠P+m∠Q = 180°
∵ The sum of consecutive interior angles is 180°
⇒ m∠P + 130° = 180°
⇒ m∠P = 180° – 130°
⇒ m∠P = 50°
Again, m∠R + m∠S = 180°
∵ The sum of consecutive interior angles is 180°
⇒ 90° + m Z S = 180°
⇒ m∠S = 180° – 90° = 90°
Yes; there is one more method of finding m∠P if m∠R is given and that is by using the angle sum property of a quadrilateral.
We have,
m∠P + m∠Q + m∠R + m∠S = 360°
⇒ m∠P + 130° + 90° + 90° = 360°
⇒ m∠P + 310° = 360°
⇒ m∠P = 360° – 310° = 50°.
We hope the NCERT Solutions for Class 8 Maths Chapter 3 Understanding Quadrilaterals Ex 3.3 help you. If you have any query regarding NCERT Solutions for Class 8 Maths Chapter 3 Understanding Quadrilaterals Ex 3.3, drop a comment below and we will get back to you at the earliest.